G-KSVD字典及其在滚动轴承故障信号稀疏表示中的应用
2021-08-16郜文清潘作舟张光雅樊凤杰
孟 宗 郜文清 潘作舟 张光雅 樊凤杰
燕山大学电气工程学院,秦皇岛,066004
0 引言
滚动轴承作为旋转机械的关键部件,其运行状态直接影响旋转机械设备的安全可靠运行[1-2],因此,对滚动轴承进行故障诊断具有重要意义[3-4]。在滚动轴承诊断故障中,振动信号分析方法是最常用的方法之一。依据传统的香农采样定理对滚动轴承振动信号采样时会产生大量数据,从而加大了信号后续分析处理的难度。近年来,随着稀疏表示的出现,基于稀疏表示的滚动轴承信号分析方法使数据量得到有效降低,信号处理难度也得以减小。
稀疏表示包含字典设计与稀疏编码两个部分[5-6]。在假定字典已知的前提下,利用稀疏编码能够求解出表示输入信号的稀疏向量,因此,字典是稀疏表示的关键,它主要分为分析字典和学习字典两类。分析字典能够利用固定的函数基直接得到字典[7],在提取信号中的冲击成分、简谐振动及其他瞬态现象方面较为直接有效。然而随着信号的变化,基函数也要随之变化,由此使得信号分析的难度增加,在具体的应用中普适性不高。不同于分析字典,学习字典是从数据中训练得到的字典,具有更好的稀疏度和重构精确度[8-9]。目前,相关学者已经针对学习字典提出了一系列压缩信号的方法,用以解决复杂信号难以处理的问题。AHARON 等[10]基于K-means聚类思想,首次提出了K-奇异值分解(K-SVD)算法。YANG等[11]针对相同模式下周期性出现的长信号,提出了一种基于移位不变字典学习的故障诊断法。LIN等[12]针对K-SVD算法在故障信号较长时引起的时间成本增加的问题,提出了以小段含冲击时域信号进行滑动窗口字典学习的新式去噪K-SVD方法。乐友喜等[13]提出一种完备总体经验模态分解与K-SVD学习字典算法相结合的地震信号去噪方法。QIN等[14]提出了一种基于自适应火花停止准则的OMP算法,进而提出了一种新的K-SVD信号矩阵和初始瞬态字典的构造方法。SHAO等[15]针对标签一致K-SVD算法,在正则化1字典学习算法中应用标签信息,提出了标签嵌入字典学习方法。然而,上述有关K-SVD的算法中,由于缺少对原子相干性的分析,降低了重构信号与原始信号所含故障信息的相似度,从而导致故障诊断准确度的下降。奇异值分解[16]作为K-SVD训练字典过程中的关键环节,具有优良的数值稳健性。ZHAO等[17]提出能够描述复杂信号奇异值突变状态的奇异值差分谱,用来实现有效奇异值的自动选取。REZA等[18]利用奇异值分解和Hankel矩阵实现了对滚动轴承时域振动信号及其频谱的去噪处理。LI等[19]针对早期微弱故障信号,提出了一种基于SVD和OFBE的滚动轴承故障特征提取方法,利用SVD实现了信号降噪。ZHU等[20]结合BCS和嵌入式SVD提出一种图像加密方案,以此来增强方案的鲁棒性。由上述文献可知,奇异值分解能够提高信号处理的精度,同时奇异值的选取关系到奇异值分解的降噪效果,然而在训练字典中缺少合适的指标来选取有效的奇异分量,从而导致重构信号信噪比的下降。
在对学习字典进行训练的过程中,针对奇异分量之间的相干性,本文提出了一种基于自相关函数脉冲能量比(auto-correlation function pulse energy ratio,ACFPER)的G-K奇异值分解(G-KSVD)训练字典。ACFPER指标能够优化奇异分量的选择,获取最优原子;结合最优原子的学习字典算法能够在减小噪声的同时,增强冲击信号;G-KSVD算法在迭代更新中由于反馈的减少,可降低算法的时间成本。
1 K-SVD学习字典
在信号稀疏表示的过程中,K-SVD算法是目前应用最广的字典学习方法,其核心思想是对字典原子进行逐列更新,目标函数为
(1)
其中,Y是由原始信号构成的训练样本,D是学习字典,‖·‖F是lF范数,xi是系数矩阵X的第i列向量,T0是稀疏度。K-SVD算法首先通过固定字典D,利用OMP算法对稀疏系数X进行更新,然后通过优化问题对字典进行逐列更新。更新原子的误差矩阵El的计算公式[9]如下:
(2)

(3)
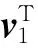
2 基于G-KSVD学习字典的信号重构
2.1 信号预处理
轴承信号在进行稀疏表示及压缩重构的过程中,对信号进行一定的预处理,能够降低信号在稀疏表示过程中的难度。本文在对实际信号预处理时主要考虑以下两个问题:一是通过传感器采集到的轴承信号通常是包含噪声的,这增加了数据处理等的难度;二是数据的偶然性、单一性会给实验结果带来一定的误差,需要通过多次实验验证。
在实验过程中,需要对所提方法的有效性进行判断。然而,实验采集到的轴承信号长度较大,导致单次完整实验所消耗的时间过长,无法及时有效地读取信号特征量。因此,本文在获取到轴承信号之后,对信号进行分段处理[21],并对分段后的信号进行压缩重构,减少信号的冗杂度。对轴承信号的分段过程如下:
(1)确定信号总长度N、信号的段数φ,每段信号的长度n,则三者关系为
N=φn
(4)
记第φ段信号为sφ,则原始信号s可表示为
s=[s1s2…sφ…sφ]
(5)
(2)利用G-KSVD算法从信号sφ中训练出稀疏字典Dφ,则
(6)
以字典D作为先验条件对信号进行重构,得
(7)
记录每段信号的特征量。
(4)对信号进行降维整合,得到重构信号:
x=[x1x2…xφ…xφ]
(8)
2.2 自相关函数脉冲能量比
特征分量的有效识别有利于对故障信号中的脉冲序列进行准确提取[22-23]。基于此,本文针对敏感原子对故障信号检测中精度的影响,提出自相关函数脉冲能量比,并以此为标准筛选敏感原子,识别有效的特征分量。
在时域中,相关函数[24]是信号相关性的平均度量,本文根据相似度这一特性,利用相关函数对信号进行处理,选用的相关函数分别为互相关函数和自相关函数,并根据实验结果来选择较优的相关函数。通过实验发现,自相关函数可以更加准确地检测出脉冲序列。噪声信号的自相关函数集中分布在零点处,原信号的自相关函数则能够较好地保留脉冲信号的周期[25],因此,对信号进行自相关处理能够减少噪声对冲击脉冲的影响。由于信号幅值以及窗口长度的作用,信号的自相关函数在传统的算法中会出现其首个极值点估值起伏较大的问题。为改善这一情况,本文采用归一自相关函数R(t)对含噪信号进行处理:
(9)
其中,n0表示信号的窗口长度,x(t+i)表示在t+i时段内截取的信号,τ表示时间延迟,δ为信号标准差。对信号进行自相关归一化后,信号的最大幅值为1,能够减小归一化前信号的幅值波动,增强信号的鲁棒性。
为了计算信号的归一自相关函数及N的长度,对测量信号进行Hilbert变换得到包络信号s(t),并对信号进行去直流处理后得到信号l(t):
y(t)=|s(t)|
(10)
(11)
(12)
Teager能量算子[26-27]能够测量单个时变信号在机械过程中产生的能量,具有较高的时间分辨率,并且能自适应地检测信号的瞬时变化。Teager能量值通过跟踪信号的瞬时能量能够检测信号的冲击脉冲,为信号分析提供了新的途径。对于离散信号x(n),其能量算子的定义为
φ[x(n)]=[x(n)]2-x(n-1)x(n+1)
(13)
Teager能量信号包含由脉冲故障特征引起的幅度调制和频率调制的信息。Teager能量算子在提高冲击信号信噪比和表述信号特征方面具有很大优势。基于此,本文提出了自相关函数脉冲能量比(ACFPER)RAC:
(14)
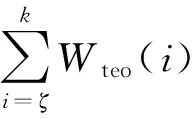
2.3 G-KSVD学习字典
为了提高传统的K-SVD学习字典的精度,在字典更新阶段,G-KSVD算法以ACFPER为指标选取含有冲击脉冲的敏感原子,通过归一自相关函数对信号进行降噪,再由Teager能量算子追踪信号的瞬时能量,使更新的字典原子中包含更多的故障信息,从而提升故障信息识别过程中的准确率。
传统的K-SVD学习字典算法中,在对系数矩阵列向量以及字典原子进行更新的过程中,会再次调用对误差矩阵进行奇异值分解相关的函数,考虑到时间因素对故障诊断效率的影响,本文在确定敏感原子后,通过对字典原子进行直接赋值、归一化处理,减少反馈过程的处理,降低算法的时间成本。算法的具体步骤如下:
(1)选取训练样本信号Y,确定初始字典原子长度N,稀疏度K,算法迭代次数J。根据信号Y构造初始字典。
(2)利用OMP算法对数据进行稀疏表示,获得信号在当前字典下的稀疏系数矩阵X。
(3)固定系数矩阵X,对X中每列元素αi进行赋值,开始迭代。
(4)根据式(2)计算出误差矩阵Ei,并确定αi中非零项的位置索引集合Ωi。

(6)对矩阵U中每个原子uj求取ACFPER值,得到特征量ACFPER最大时对应的原子uj,并用其来更新字典单元。
(7)为了减小奇异分量间差异对系数矩阵更新、重构信号精度的影响,确定矩阵中最接近均值的奇异分量的位置索引ε。
(8)利用索引对系数矩阵X中的列元素进行更新:
(15)
(9)利用(6)中所得原子uj对第i列字典元素di进行赋值及归一化处理。
(10)迭代停止后,输出字典D和稀疏系数矩阵X,进行二次重构。
3 仿真实验
为验证本文算法的降噪效果,针对振动信号的特点,构造以下仿真信号进行实验:
(16)
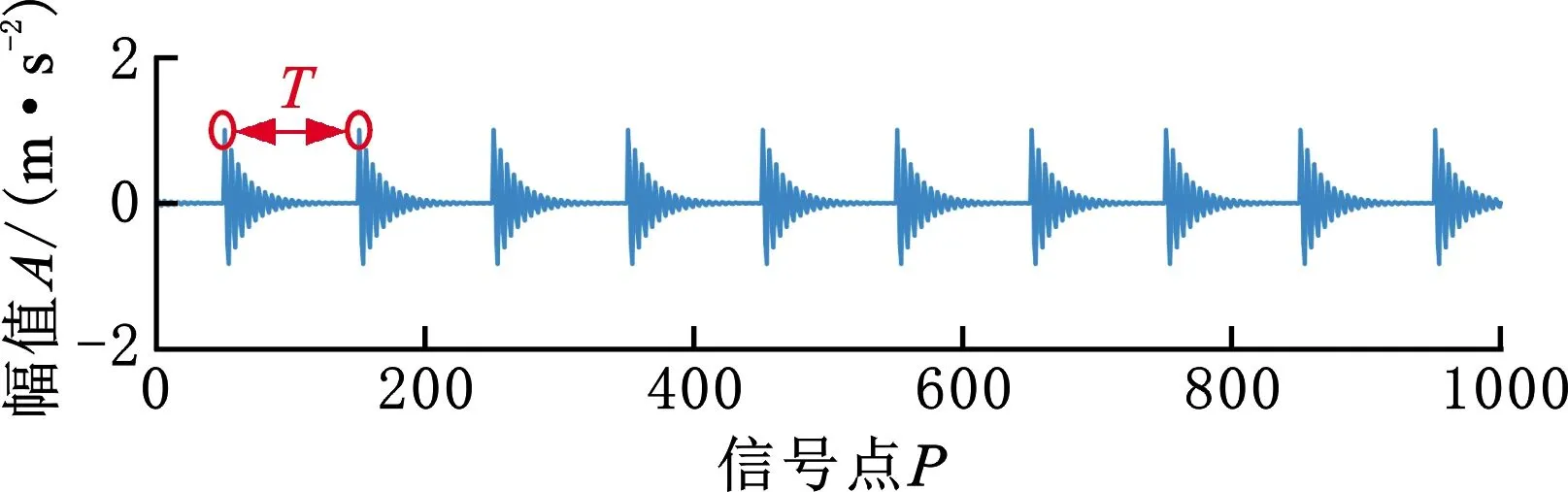
本文中参数设置如下:As=0.01,f=200,z=0.05,周期T=0.1 s,采样频率fs=1000 Hz。在信号y中加入不同噪声强度的高斯白噪声n,以模拟不同噪声环境下采集到的信号。此处以0 dBW的高斯白噪声为例,绘制图1所示信号,并计算3种信号的归一自相关函数,结果如图2所示。
从图1、图2可以看出,周期脉冲信号的归一自相关函数能够较好地保留信号周期;噪声信号的归一自相关函数集中在零点附近,即在零点处幅值较大,在非零点处幅值接近0;混合信号的归一自相关函数在零点处幅值较大,在非零点处的脉冲周期与原始信号相同。由此可以看出,归一自相关函数能够在降低信号中噪声成分的同时,保留信号脉冲。因此,基于ACFPER改进的G-KSVD算法能够达到降低噪声信号的目的。
(a)脉冲信号

(a)脉冲信号
为了进一步验证G-KSVD算法的降噪效果,利用G-KSVD算法对字典原子进行特征量的学习以得到新的稀疏字典,再通过测量矩阵对信号进行重构,分析重构信号的特征量。因所加噪声强度的不同,字典学习的效果不同,重构所得的信号精度也有差异。本文对所提方法的适用范围进行验证,判断G-KSVD算法的应用效果及区间。由于实验信号的采集会受到各种不定性因素的影响,无法衡量确切的噪声强度,故本文通过仿真信号模拟不同强度的噪声环境,并对同一噪声环境下的G-KSVD算法及K-SVD算法进行验证和对比,来判断两者的去噪效果。
在信号处理过程中,为了衡量处理后信号中的噪声含量,引入信噪比这一概念。信号强度PS与噪声PN的比值定义为信噪比(signal-to-noise ratio,SNR):
RSN=10lg(PS/PN)
(17)
由上式可知,噪声的功率越小,信噪比越大,同理,噪声的功率越大,信噪比越小。为验证本文方法的应用环境以及两种算法的有效性,分别对加入不同强度噪声的信号进行G-KSVD字典学习和K-SVD字典学习,利用信噪比衡量两种方法的去噪效果。由于K-SVD算法在强噪声环境下效果较差,故从0 dBW的噪声环境开始,以-5 dBW和5 dBW为一个单位长度,通过500次重复实验后,对不同强度噪声环境下K-SVD算法和G-KSVD算法的有效性进行验证,记录实验结果并求均值,见表1。
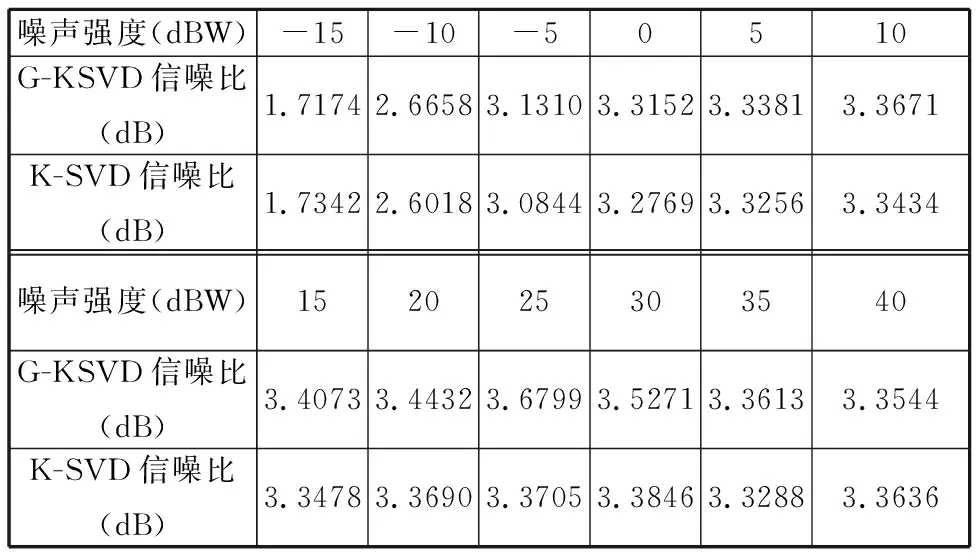
表1 不同噪声环境下G-KSVD算法和K-SVD算法的信噪比
为了更清晰地对比以上两种算法的有效性,确定G-KSVD算法的阈值,对表1中数据进行处理。将G-KSVD 信噪比RSN1与K-SVD 信噪比RSN2的差值定义为差值信噪比(DSNR):
RDSN=RSN1-RSN2
(18)
当G-KSVD算法与K-SVD算法的差值信噪比大于零时,G-KSVD算法的去噪效果优于K-SVD算法的去噪效果。将不同强度噪声下的差值信噪比绘入图3。

图3 G-KSVD算法与K-SVD算法的差值信噪比
由图3可以看出,当噪声强度在-10~35 dBW这一区间时,差值信噪比均大于零,说明G-KSVD算法在该区间的信噪比大于K-SVD算法的信噪比,即G-KSVD算法的去噪效果优于K-SVD算法。噪声强度为-15 dBW和40 dBW时,差值信噪比小于零,说明G-KSVD算法在这两点的信噪比小于K-SVD算法的信噪比,降噪效果有所下降。为了精确确定G-KSVD算法的应用区间,以1 dBW为一个单位长度对-15~-10 dBW及35~40 dBW两个区间进行仿真实验,记录数据见表2、表3。同理,为了更直观地观察G-KSVD算法的适用环境,将两个区间中G-KSVD算法和K-SVD算法的差值信噪比分别绘入图4。

表2 G-KSVD算法和K-SVD算法的信噪比(-15~-10 dBW区间)

表3 G-KSVD算法和K-SVD算法的信噪比(35~40 dBW区间)
由图4可以看出,在-15~-10 dBW区间内,-13~-10 dBW这一区间内的差值信噪比均大于零,而-15 dBW和-14 dBW的差值信噪比小于零,因此,G-KSVD算法应用环境的噪声强度下限为-13 dBW。此外,在35~40 dBW区间内,35~38 dBW之间的差值信噪比均大于零,而39 dBW和40 dBW的差值信噪比小于零,由此可以确定G-KSVD算法所应用环境的噪声强度上限为38 dBW。

(a)-15~-10 dBW区间的差值信噪比
综合比较以上数据,G-KSVD算法的应用范围为-13~38 dBW,即在这一区间内,同一噪声强度下G-KSVD算法的去噪效果优于K-SVD算法的去噪效果,在故障诊断的过程中,G-KSVD算法能够减少噪声对冲击序列的影响,更加准确地识别冲击脉冲,对于故障特征的提取也更加准确。
4 实验与分析
为进一步验证本文算法对实际信号的应用效果,采用图5所示燕山大学机械故障综合模拟实验台的内圈数据进行实验。实验台由两个3/4英寸ER-12K转子轴承组成。驱动系统中电机转速n始终保持在1200 r/min,基频fB=n/60=20 Hz。装载系统由两个转子组成,转子的厚度为15.9 mm,自重为6.5 N,直径为151.3 mm。采集系统使用NI 9234加速采集卡,其频率为12.8 kHz,轴承频率为32 Hz,采集时间为64 s。为验证本文所提的自相关函数脉冲能量比对有效特征分量的提取效果,对ACFPER中涉及到的函数进行验证。由于振动信号的长度较大,为降低数据处理的压力,对信号进行分段训练,并计算每段信号的信噪比,最后根据信噪比的均值判断信号的重构效果。为减小随机性带来的误差,本文中实际实验的结果是通过500次重复实验后所求的均值。

图5 机械故障综合模拟实验台
4.1 构造ACFPER时相关函数的比较分析
为验证本文所涉及的归一自相关函数、自相关函数、互相关函数的去噪效果,以及与原信号的相似度,分别利用3种相关函数对信号进行降噪处理,结果如图6所示。可以看出,信号的归一自相关函数和自相关函数与原信号的相似度较高,保留了原始信号的冲击序列周期,而信号的互相关函数只在2×104处有明显脉冲,与原信号的相似度较低。观察前两个相关函数后发现,信号在零点处的幅值最大,且大于原始信号在零点处的脉冲序列,而在非零点处的幅值近似于原始信号的脉冲序列,说明前两个相关函数有较好的降噪效果,且噪声信号主要集中在零点附近。
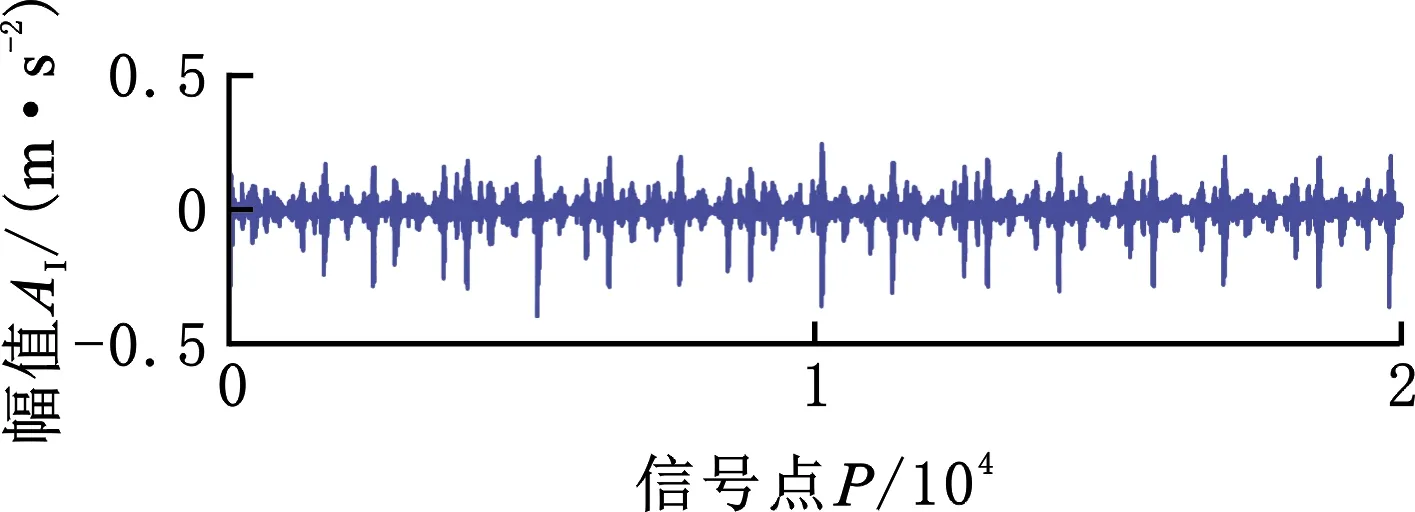
(a)内圈故障信号
分别将归一自相关函数、自相关函数以及互相关函数应用到ACFPER中,构造学习字典G-KSVD、G-KSVD1、G-KSVD2,通过3个不同的学习字典对数据进行训练,得到的信噪比见表4。为了更加充分地描述本文算法的优越性,本实验同时记录了各学习字典的峰峰值,以此反映不同相关函数对应的信号幅值大小。

表4 不同相关函数对应学习字典训练数据的特征量
由表4可以看出,G-KSVD学习字典的信噪比最大,G-KSVD1次之,G-KSVD2信噪比最小,所以,相比较其他两种字典,G-KSVD的去噪效果更好,提取到的冲击序列能够包含更多的有用信息。就峰峰值而言,G-KSVD字典的值大于其他两种字典,由此可以看出,通过G-KSVD学习字典重构的信号的幅值更大,能够更准确地识别冲击序列。
4.2 构造ACFPER时参数变化对信号稀疏表示的影响
噪声信号的相关函数在零点处达到最大值,其能量主要集中分布在零点附近[26]。脉冲故障信号的相关函数则保留了脉冲周期,其能量基本不会受到影响。因此,脉冲故障和噪声可以通过归一自相关函数进行分离。
在式(14)中,ξ和k值的选取均会对学习字典的稀疏效果产生影响。由于噪声信号的归一自相关函数在第一个极值点处的能量较为集中,故当ξ=2时,学习字典能达到更好的去噪效果,为了验证这一结论,分别取ξ=1、ξ=2和ξ=3进行实验。同理,对k的取值进行验证,文献[24]中建议k=3,因此,本文对k=3附近的取值进行验证,其中,信号的信噪比见表5。除此之外,将通过不同字典压缩重构的信号峰峰值记录于表6。

表5 不同ξ值和k值对应学习字典训练数据的信噪比

表6 不同ξ值和k值对应学习字典训练数据的峰峰值
由表5可以看出,ξ=1时,信噪比在k=3时达到最大值1.0805 dB;ξ=2时,信噪比在k=3时达到最大值1.1096 dB;ξ=3时,信噪比在k=4时达到最大值1.0742 dB。对比这3个数据发现,当ξ=2及k=3时,信噪比达到最大值,说明此时GSKVD的去噪效果最好,精度更高,噪声信号对冲击序列的影响最小。
由表6可以看出,ξ=1时,峰峰值在k=2时达到最大值0.6894 m/s2;ξ=2时,峰峰值在k=3时达到最大值0.6944 m/s2;ξ=3时,峰峰值在k=4时达到最大值0.6864 m/s2。对比这3个数据发现,当ξ=2及k=3时,峰峰值最大,说明冲击信号的幅值更大,有利于后期的故障提取。
综上,当ξ=2及k=3时,G-KSVD学习字典取得的效果较优。对比信噪比后发现,G-KSVD算法在对故障信号压缩重构的过程中能够有效地降低信号中的噪声成分,从而达到降噪的效果。此外,对比峰峰值后发现,G-KSVD算法在对故障信号压缩重构的过程中能够增加脉冲信号的幅值,说明本文方法能够增强故障信号中的冲击成分,从而提高故障诊断的准确度。
4.3 基于ACFPER改进的G-KSVD0学习字典
为验证引入ACFPER的学习字典的优越性,将时间优化前的学习字典称为G-KSVD0学习字典,以此区分G-KSVD学习字典。采用燕山大学机械故障综合模拟实验台的内圈故障数据,分别用传统的K-SVD算法和G-KSVD0算法进行训练,实验结果如图7所示。
图7中,重构信号1为经过K-SVD算法重构所得的信号,重构信号2为经过G-KSVD0算法重构所得的信号。由图7可知,三种信号幅值的上阈值均为0.5 m/s2,下阈值均为-0.5 m/s2。此外,由信号中峰值点的坐标可以看出,原始信号中冲击信号的峰值最小,重构信号1次之,重构信号2中冲击信号的峰值最接近阈值。由此可知,G-KSVD0算法在降低噪声的同时,能够增强信号中的冲击成分,从而提高故障诊断的准确性。所得特征量数据见表7。

(a)原始信号
由表7可以看出,G-KSVD0算法的信噪比大于K-SVD算法的信噪比,说明G-KSVD0算法的去噪效果优于K-SVD算法,并且通过降噪处理提高了信号重构的精度,降低了噪声部分对冲击序列的影响。同时,G-KSVD0算法的峰峰值大
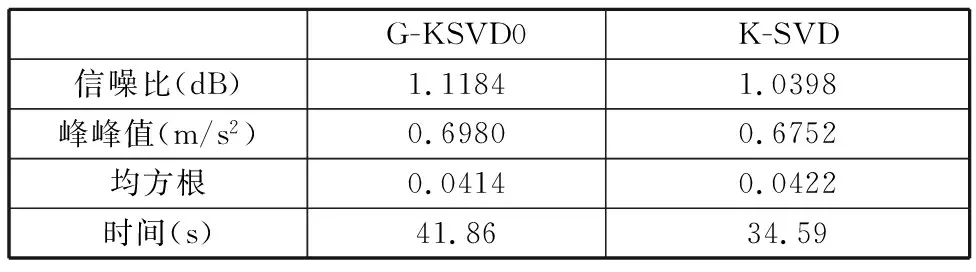
表7 G-KSVD0与K-SVD字典的实验数据
于K-SVD算法的峰峰值,说明G-KSVD0算法所得信号的幅值大于K-SVD算法的幅值,信号得到了增强,方便故障特征的识别与提取。最后,为了判断本文算法的鲁棒性,对两种算法求均方根值,由表7可知,G-KSVD0算法的均方根略小于K-SVD算法的均方根,说明经G-KSVD0算法重构后的信号分布更加稳定,受噪声影响较小,有较好的鲁棒性。但是G-KSVD0算法的运行时间大于K-SVD算法的运行时间,增加了算法的时间成本。
4.4 G-KSVD学习字典
G-KSVD0学习字典是从样本中训练而来,经过奇异分量的ACFPER计算,选择包含脉冲序列较多的原子,对字典原子进行更新,进而得到有效的稀疏表示,实现信号的压缩重构,减小了信号传输、处理上的压力。然而,由于各原子的ACFPER指标计算增加了算法的运算复杂度,从而影响了算法的运行时间,增加了故障诊断的时间成本,故本文在字典更新阶段采用减少反馈层的方法来减小算法的时间成本,构造新的学习字典G-KSVD。为了检验这一效果,分别利用改进的G-KSVD算法和K-SVD算法训练数据,实验结果如图8所示,表8中的实验数据是经过500次的重复实验后求均值得到的。

(a)原始信号

表8 G-KSVD算法、G-KSVD0算法与K-SVD算法的特征量均值
图8中,重构信号1为经过K-SVD算法重构所得的信号,重构信号2为经过G-KSVD算法重构所得的信号。由图8可以看出,算法经过减少反馈层之后,重构信号2中冲击信号的幅值是最接近阈值的。由表8可知,虽然G-KSVD算法的降噪效果和鲁棒性不及G-KSVD0算法,但是效果相差较小,而且G-KSVD算法的时间成本明显小于G-KSVD0算法的时间成本。除此之外,G-KSVD算法的信噪比、峰峰值均大于K-SVD算法的信噪比、峰峰值,说明G-KSVD算法不仅能够降低重构信号中的噪声,而且可以增强信号中的冲击成分。G-KSVD算法的均方根小于K-SVD算法的均方根,说明G-KSVD算法的鲁棒性优于K-SVD算法的鲁棒性。在时间方面,G-KSVD算法所耗时间均值为23.52 s,K-SVD算法所耗时间均值为34.59 s,由此可以看出,G-KSVD算法的运行时间明显小于K-SVD算法的运行时间。因此,通过减少反馈能够在保证精度的前提下有效地缩短算法的运行时间,从而达到降低时间成本的目的。
5 结论
(1)针对轴承信号复杂冗长的特性,本文在信号预处理过程中对信号进行分段,并对分段后的信号压缩重构,从而提高信号分析的效率。同时,为了分析学习字典中原子间的相干性,本文提出自相关函数脉冲能量比这一指标,通过归一自相关函数实现信号降噪的同时,通过Teager能量算子追踪瞬时能量,增强重构信号中的冲击成分,从而达到识别有效特征分量的目的。
(2)针对学习字典中缺乏的最优原子选择问题,提出一种G-KSVD学习字典算法,该算法以ACFPER作为奇异值分解过程中有效奇异分量的选择指标,通过有效的奇异分量实现最优原子的选取,形成新的学习字典。该算法不仅优化了降噪效果,而且增强了信号脉冲,提高了轴承信号重构过程中的准确度。
(3)由于ACFPER的求解会增加G-KSVD算法的计算复杂度,故本文在字典和系数矩阵的更新过程中通过减少反馈过程来降低时间对算法的影响。滚动轴承信号的实际实验结果表明,本文算法所消耗的时间成本低于传统K-SVD算法的时间成本。
