Mie散射中递推方法的比较

林乐科，赵振维，张鑫

（中国电波传播研究所，山东 青岛 266107）

Mie理论对于无损介质中均匀球的散射问题给 出了一个精确的解答[1-2]。它广泛应用于气体分子、气溶胶、云雾水滴、小雨滴等近球形粒子的X射线、可见光、红外、微波、毫米波的电磁散射、辐射气象、医学、遥感、通信、雷达等多个领域[3-15]。Mie理论的准确计算有着重要的现实意义，例如球形水滴的散射是云雾和降雨衰减计算的基础等，但其系数中包含复杂的函数形式（球贝塞尔函数及其导数），计算复杂，难以精确求解。为此提出了几种递推的方法[16-18]，便于计算。文献[18]对于赵递推和正向递推方法的收敛性进行了比较，但是没有比较倒递推方法，也没有比较不同递推方法对于截断项数的收敛特性。为此，文中比较了这几种递推方法的收敛性能、截断项数的鲁棒性等，发现如正确选择参数，赵递推公式最准确、适用范围最广。

1 Mie理论数值计算

假定介质球的折射指数为m，半径为r，其周围介质为自由空间，自由空间波长为λ0，则Mie理论系数的计算公式为[16-17,19]：

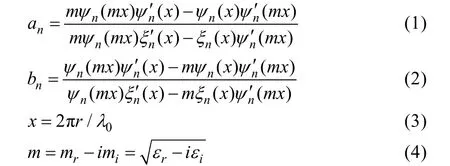
其中：

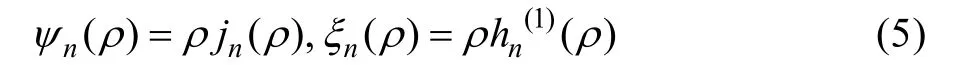
式中：ψn(ρ)、ξn(ρ)为黎卡提-贝塞尔（Riccati-Bessel）函数，jn(ρ)与hn(1)(ρ)分别为球贝塞尔函数与第一类球汉克尔函数。黎卡提-贝塞尔函数具有以下性质及递推关系：

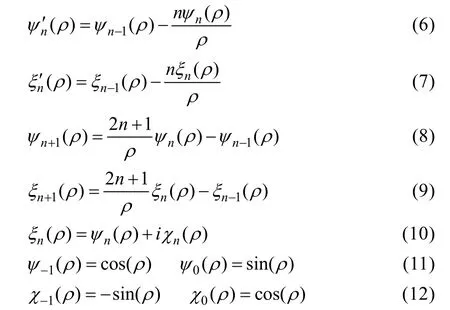
令：

由(6)、(8)、(13)可推得：

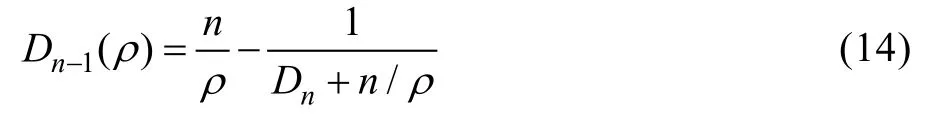
则有：

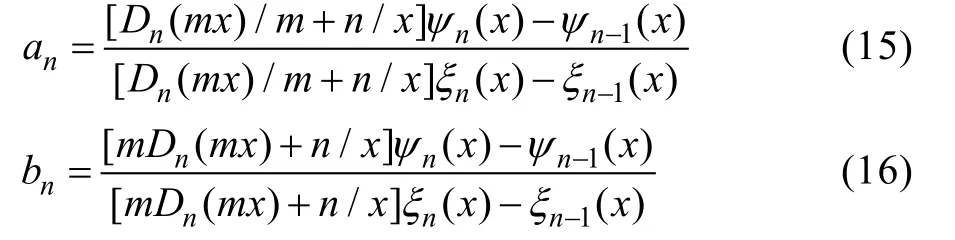
利用Mie系数计算归一化散射截面、消光截面、后向散射截面的公式为：

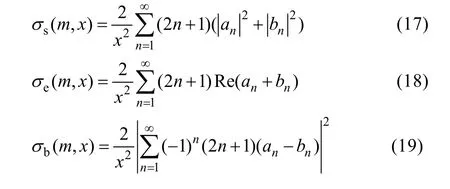
2 计算Dn的递推公式

从以上公式可以看出，影响Mie系数精度的关键是Dn的计算，其他参数都给了恰当的初值与递推公式。当球为理想导体球时，Dn=i。对于介质球，目前计算Dn的主要递推方法有以下几种。

1）倒递推公式，即直接利用式(14)，计算散射、消光截面时取其前K项，K值可取为[17]：

式中：INT[]表示取整函数。倒递推起始点为：

由此向下一直递推到D1。

2）正向递推公式[16,20]。由式(14)可推出：

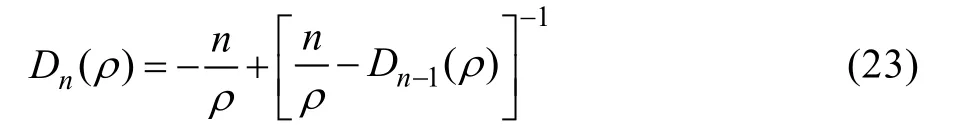
对无耗介质球：

对有耗介质球，m=mr－imi：

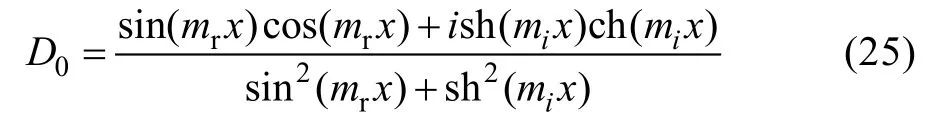
式中，sh和ch函数是无界的。当x很大时，会导致较大的计算误差和计算机溢出，赵振维将其重写为[18,21]：

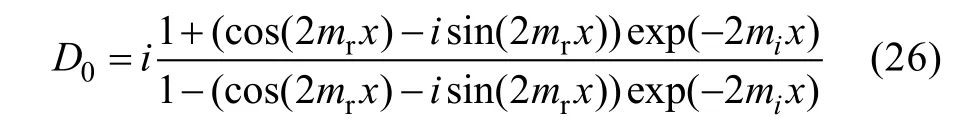
此时无论x如何增大，也不会出现计算机溢出。

3）x很大时（通常指x＞30）的正向递推公式为[18,21]：

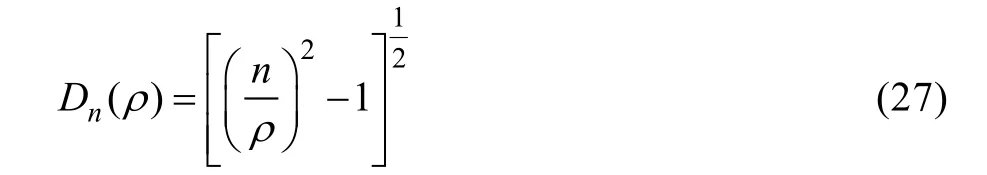
以下将其称之为赵递推公式。对于赵递推公式，当x≤30时，文中采用正向递推。

3 递推公式的比较与分析

利用Mie系数计算介质球的归一化消光截面、散射截面、后向散射截面对递推公式进行比较。由于正向递推公式中并未给出截断项，计算中采用与后向递推公式相同的截断项K。对于赵递推公式，当x＞30时，采用式(27)进行递推，否则采用正向递推公式。为全面比较，选取与文献[5]相同的折射率，分别为n=1.29‒j1.47、n=1.29‒j0.47、n=1.29‒j0.047的强、中、弱吸收球，利用3种递推公式进行计算。其对n=1.29‒j1.47的计算结果如图1—3所示，对其他2种介质球也有类似结果。可以看出，当x较小时，正向递推公式与倒递推公式结果一致。当x增大到一定值（本例中约为80）时，正向递推公式变得不稳定，计算后向散射截面时尤为显著。此时赵递推公式与倒递推公式都是连续稳定的，并趋于一致，赵递推从逻辑上是正向的，相对容易理解。

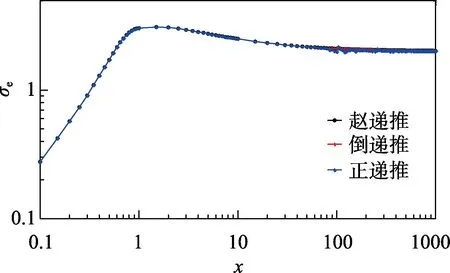
图1 归一化消光截面随x的变化Fig.1 Variation of normalized extinction cross section with x

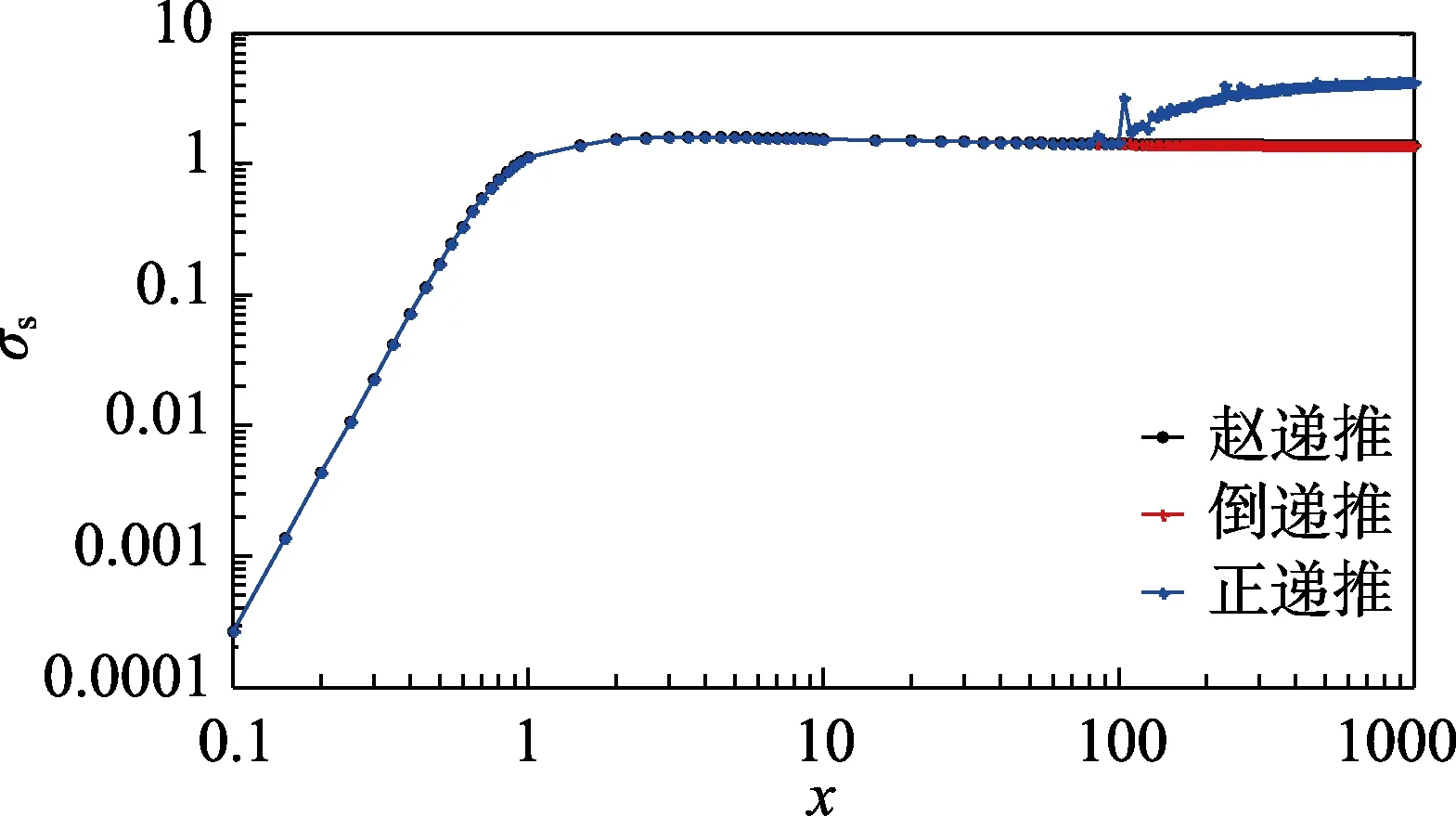
图2 归一化散射截面随x的变化Fig.2 Variation of normalized scattering cross section with x

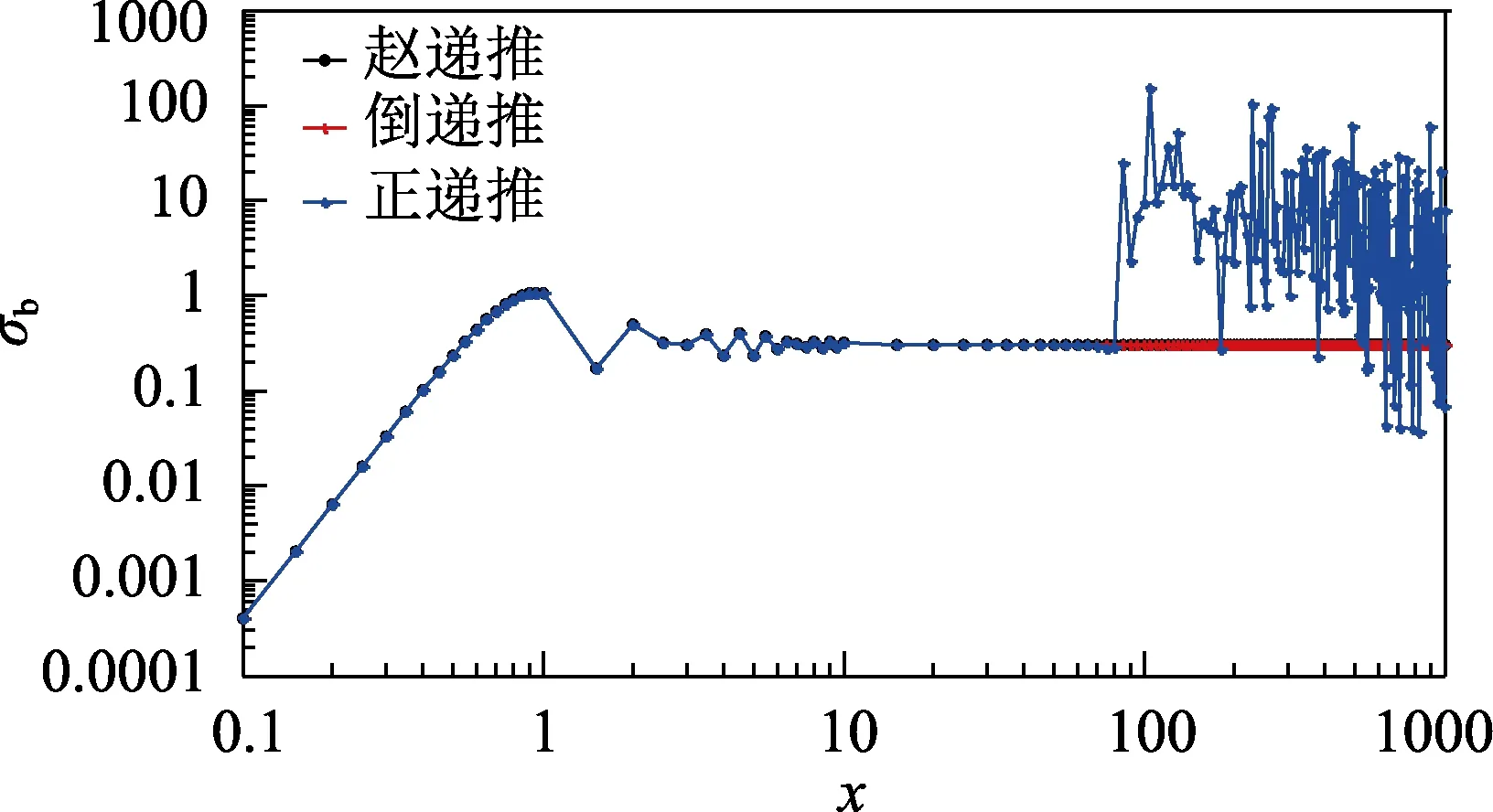
图3 归一化后向散射截面随x的变化Fig.3 Variation of normalized backscatter cross section with x

另外，由于前面的计算都采用了相同的截断项，下面分析截断项增大的情况。假设截断项数比式(22)增加200，则计算得到的倒递推公式和赵递推公式的后项散射截面如图4所示。可以看到，这时倒递推仅在x＞6时有值，而赵递推公式此时计算结果仍然是正常的。当然，随着截断项数的持续增加，赵递推公式也会出现不收敛的情况，但是显然其对截断项数的鲁棒性更强。综合上述分析，可以认为赵递推公式最准确、适用范围最广。

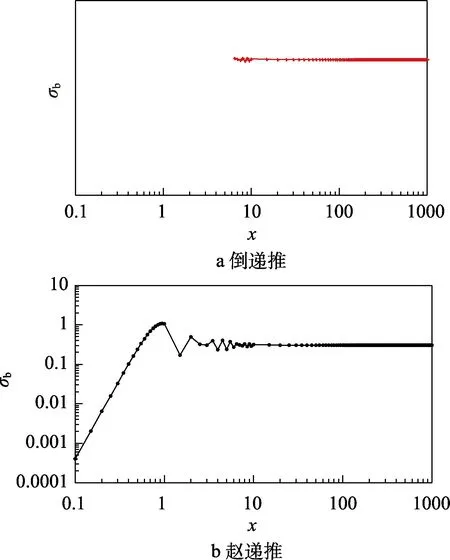
图4 归一化后向散射截面随x的变化（截断项加200）Fig.4 Normalized backscatter cross-section changes with x(truncation plus 200): a) backward inverse recursion; b) Zhao recursion

4 结语

文中对Mie系数计算中几种主要的递推公式作了分析比较，结果显示，赵递推公式是目前计算Mie系数比较理想的公式，倒递推计算结果与赵递推相似，但是在截断项数上赵递推有更好的鲁棒性。正向递推公式有一定的适用范围，超过适用范围，计算结果会发散。因此，通常情况下，建议采用赵递推公式。当然，尽管是准确的解析解，也需要实验测试来进行验证，因为公式中都采用了近似。Mie理论的实验测试存在较多困难，这是未来需要进一步研究的内容。