基于扁拱突变理论的路基下伏溶洞顶板稳定性分析

陈言章，谢子翰

（1.广东省建筑设计研究院有限公司，广东 广州 510010；2.广州市市政工程设计研究总院有限公司，广东 广州 510060）

0 引言

在我国岩溶发育地区，无论是高速公路还是市政道路在进行设计时都无法回避路基下伏溶洞这个工程难题，当路基下伏溶洞时，会极大削弱路基的承载力，导致路基塌陷，具有很大的安全隐患[1，2]。目前，设计人员在判断下伏溶洞稳定定时，主要是参考现行《公路桥涵地基与基础设计规范》（JTG3363—2019）[3]以及《岩土工程勘察规范》（GB 50021—2009）[4]，但是由于溶洞稳定性问题的复杂性，往往更多地取决于技术人员的经验性，工程上也更多的不经过计算，便保守采用充填法、强夯法等对溶洞进行处治，往往造成工程造价增加。

目前，在针对路基下伏溶洞顶板稳定性问题，学者、工程师们提出了众多理论计算模型。韩红艳等[5]将溶洞顶板简化为梁板体系，得到溶洞顶板的的跨度、厚度等参数对其稳定性的影响；赵明华等[6]考虑荷载分布的非均布性和非对称性，基于Boussinesq解求得在任意荷载分布作用下的溶洞顶板稳定性；赵明华等[7]借助复变函数，基于Schwarz 交替法分析了岩溶区存在双孔土洞时路基的稳定性问题。以上研究均是假定岩层弹性均质，但鉴于岩层破坏存在不规则、不连续等突发特点[8-10]。何忠明等[11]借助尖点突变理论模拟路基在逐层填筑过程中溶洞顶板的极限平衡状态。张成良等[12]结合以塑性应变能为准则的尖点突变理论探究了顶板厚度、溶洞跨度、上覆土层厚度、岩石强度参数对岩溶顶板极限承载力的影响。

鉴于突变理论在分析系统状态突变的非线性上具有一定的优势[13]，本文基于扁拱突变理论，建立了两端固定铰支的受力模型；然后，根据突变失稳判定条件，给出了确定路基极限承载能力以及溶洞顶板安全厚度的方法；最后，对影响顶板稳定的进行参数分析。

1 计算模型及基本假定

由于拱结构的受力合理性，在桥梁和隧道结构中得到广泛应用[14]。根据大量工程实例表明，溶洞形状大多呈拱形[15]，见图1。因此，当道路路基下伏溶洞时，本文将溶洞的受力简化为如图2 所示的平面应变模型，并做如下假定：

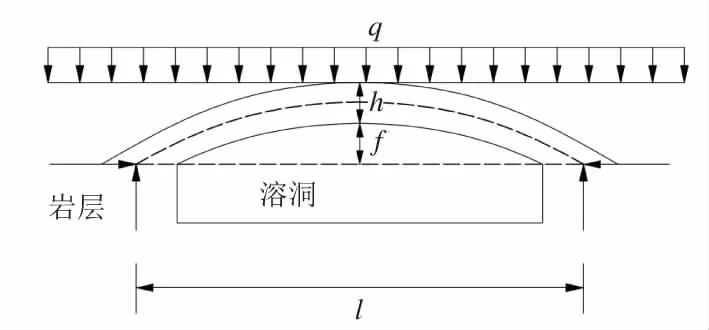
图1 路基下伏溶洞受荷体系

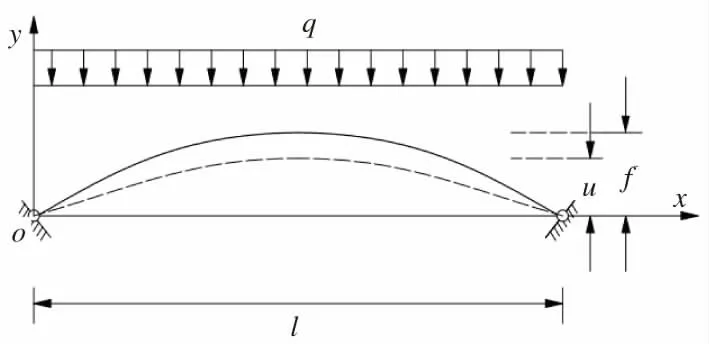
图2 简化计算模型

（1）顶板支座视为两端固定铰支，溶洞受荷前拱轴满足正弦扁拱方程。

（2）溶洞顶板上覆土层自重、路基荷载、汽车荷载等效为均布荷载作在顶板上。

图中：h 为溶洞顶板的厚度；l 为溶洞顶板的跨径；q 为作用在溶洞顶板岩层上的均布荷载；f 为受荷载前拱的矢高；u 为均布荷载作用下扁拱形变过程中拱轴中点的高度。

3 扁拱突变分析模型的建立

3.1 势函数

研究表明，图2 所示的扁拱只要高跨比相同，则不论其什么形状（如抛物线形、双曲线形），其临界荷载都极为接近[16]。因此，本文假设受荷前拱轴为正弦曲线[17]：

对于两端固定铰支扁拱，受荷载后的拱轴方程可表示为：

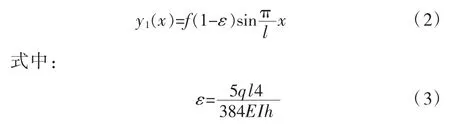
拱在荷载作用下，拱端受到推力H，故受荷后的拱轴方程应为。

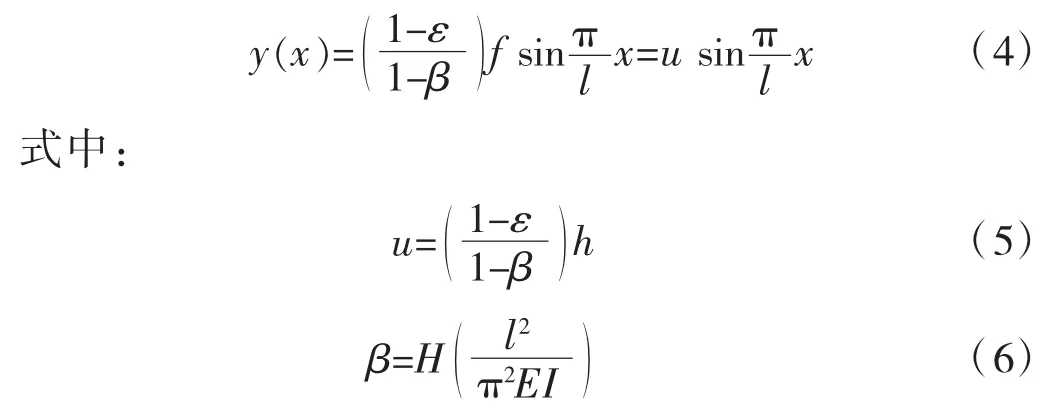
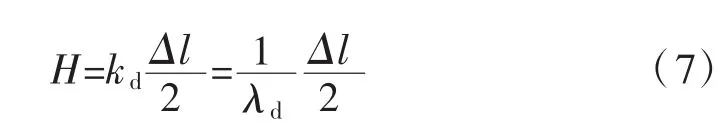
式中：kd、λd分别为弹性地基的刚度和柔度，当两端固定铰支约束时，λd=0[18]。

对于扁拱，可假定沿拱轴压力为常量，且等于水平推力，则可得到：

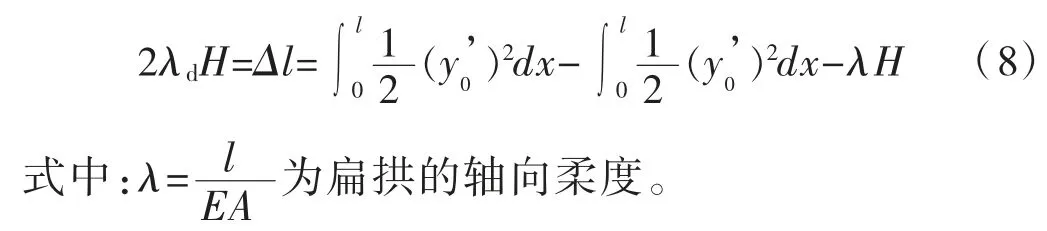
将式（1）、式（4）代入式（8）中可得水平推力为：

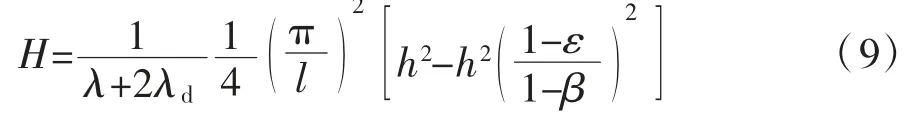
由于扁拱受荷后轴向变形不可忽略，故拱失稳的形状可由式（4）中的对称曲线表示。

当扁拱有准静态位移增量时，拱内弯曲应变能增量为：

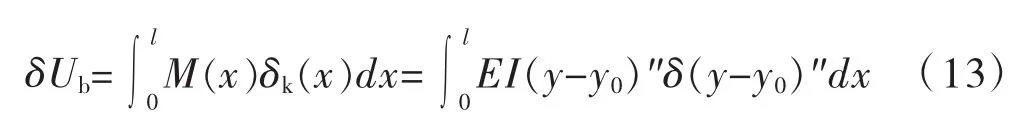
式中：k（x）=（y-y0）＂为扁拱轴线相对于初始状态的曲率M（x）=EI（y-y0）＂为扁拱在y（x）位置时拱内弯矩。

扁拱与弹性地基的应变能增量为：

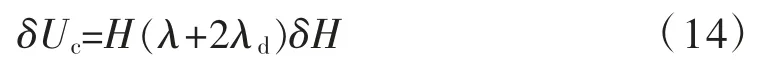
拱上的荷载势变化为：

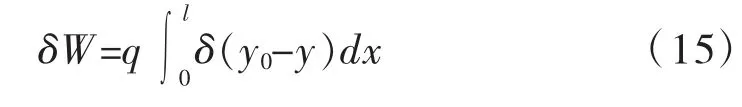
根据能量守恒原理可知[15]：

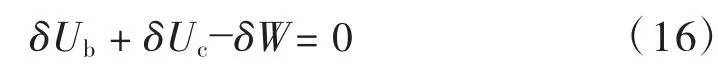
联立式（9）、式（10）、式（13）、式（14）、式（15）及式（16），整理得：

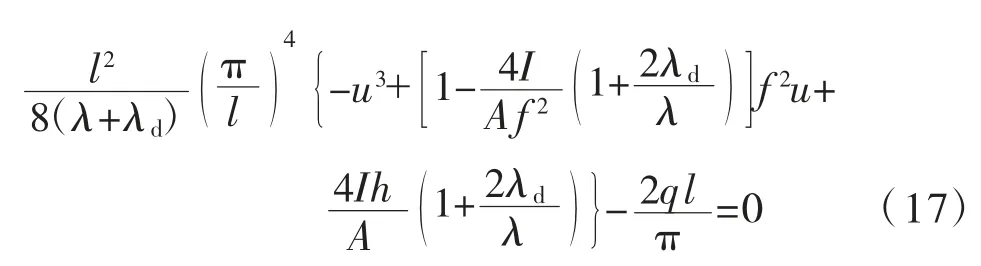
将式（17）左右两边除以f3，再利用拱轴向柔度，可得：

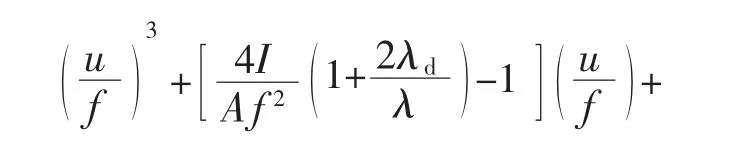
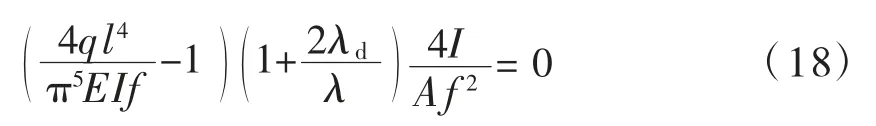
3.2 突变模型平衡曲面与分叉集方程

对式（18）作如下变量代换：

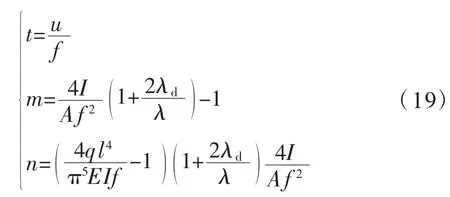
可将式（18）化成尖点突变模型平衡曲面M 的标准形式：

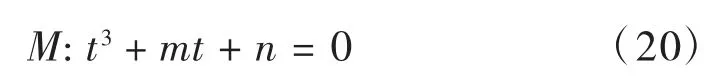
平衡曲面M 见图3。在M 上有两条垂直切线的点集S 上，存在：

联立式（20）、式（21）消去t，即可得到突变模型的分叉集方程（S 集在控制平面上的投影为分叉集，见图3）：

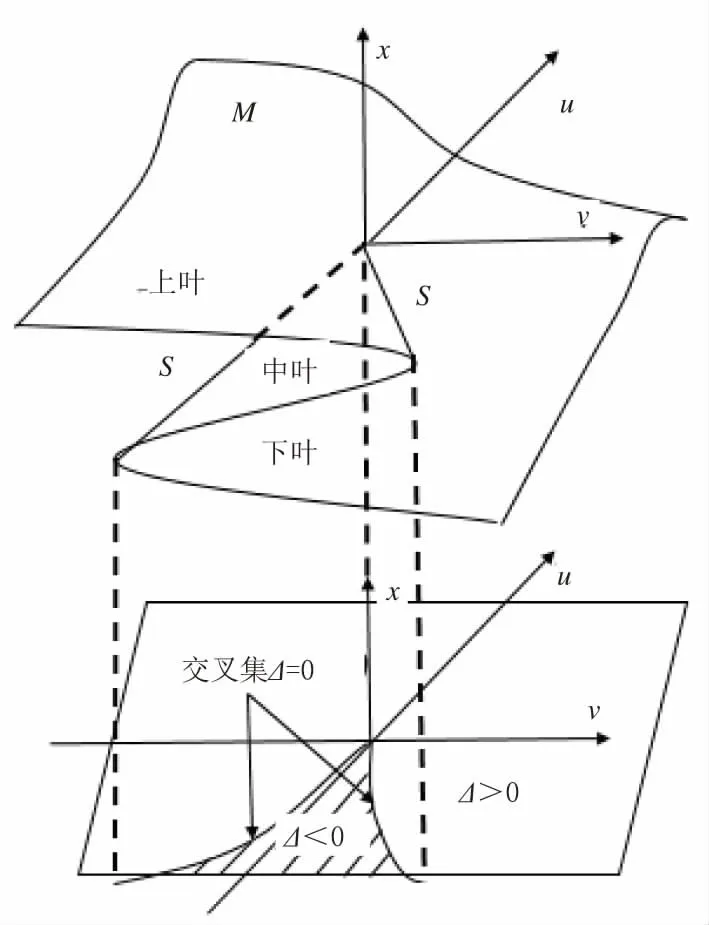
图3 突变模型平衡曲线与分叉集

因此，基于扁拱突变理论的岩溶区路基下伏溶洞顶板突变失稳与否可根据如下判据判定[19]：

（1）当Δ＞0，岩溶顶板处于稳定状态。

（2）当Δ＜0，岩溶顶板突变失稳。

（3）当Δ=0，岩溶顶板处于临界状态。

3.3 路基极限承载力及溶洞顶板安全厚度的确定

通过上述分析，要使得溶洞顶板处于稳定状态，需满足Δ≥0，将式（19）代入式（22）中，并整理可得：

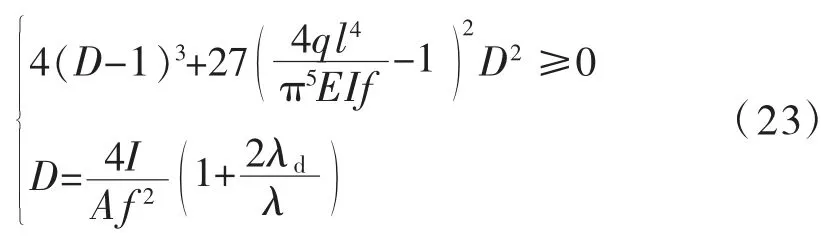
（1）溶洞顶板安全厚度的确定

（2）路基极限承载力的确定

根据式（23）可得，岩溶区路基极限承载力为：

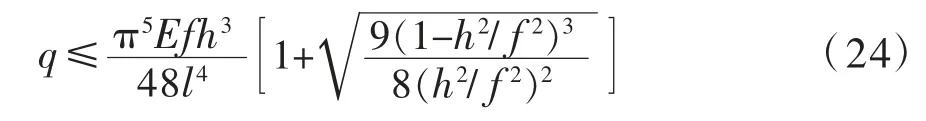
3.4 影响因素分析

根据以上分析可知，与顶板突变失稳有关的参数主要有：（1）溶洞顶板厚度h；（2）溶洞顶板跨径l；（3）溶洞顶板失高f；（4）岩层的弹性模量E；（5）溶洞顶板上覆荷载q。因此本文将针对以上四个参数对溶洞顶板的稳定性进行影响分析。

为了更加直观探究各参数对顶板稳定性的影响，引入无量纲参量k，将式（24）化简为：

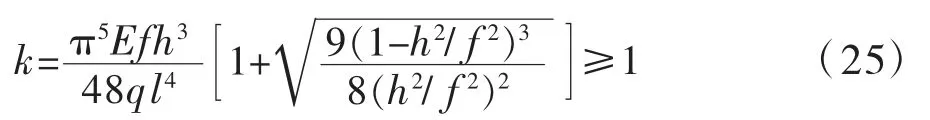
当k 不小于1 时，表明溶洞顶板处于稳定状态，反之则易发生失稳。

3.4.1 溶洞顶板厚度的影响分析

为探究溶洞顶板厚度对其稳定性的影响，令q=100 MPa，E=19 GPa，f=4 m，l 为12 m、15 m、18 m，并使溶洞顶板厚度h 分别为0.5 m、1.0 m、2.0 m、3.0 m、4.0 m 时，代入式（25）可得，溶洞顶板厚度h 对k 的影响，见图4。

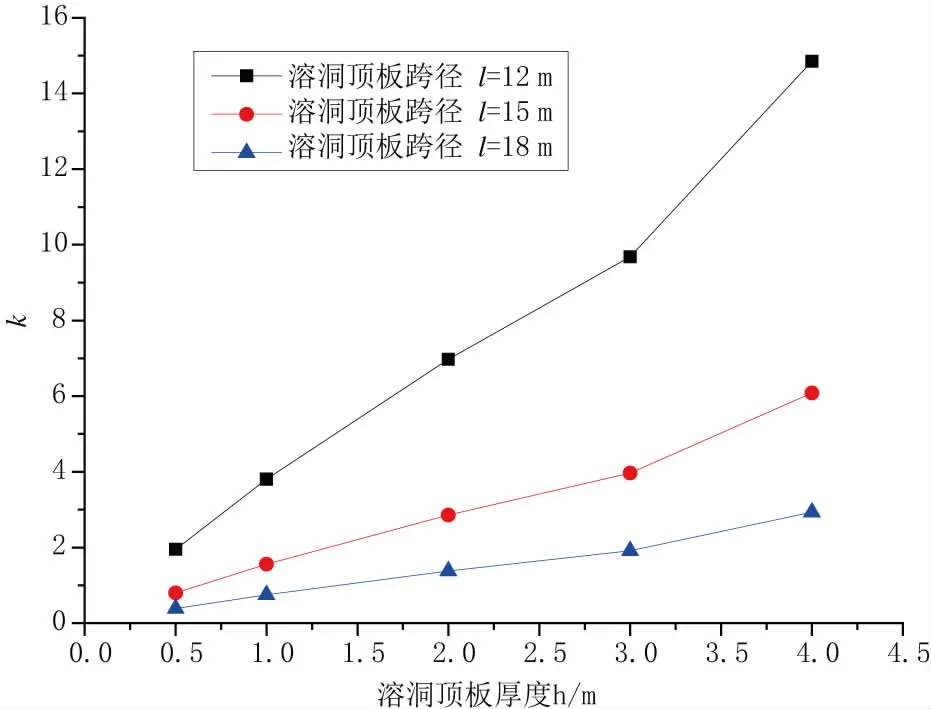
图4 溶洞顶板厚度影响分析

通过图4 可知，随着溶洞顶板厚度的减小，无量纲参量k 随之减小，当溶洞顶板厚度达到某一临界厚度时，k 将由大于1 的值变化到小于1 的值，此时顶板也将发生失稳。如当溶洞顶板跨径为15 m 时，此时溶洞顶板的失稳的临界厚度约为0.63 m。

3.4.2 溶洞顶板跨径的影响分析

为探究溶洞顶板跨径对其稳定性的影响，令q=100 MPa，E=19GPa，f=4 m，h 为0.5 m、1.0 m、2.0 m，并使溶洞顶板跨度l 分别为6 m、9 m、12 m、15 m、18 m时，代入式（25）可得，溶洞顶板跨度l 对k 的影响，见图5。

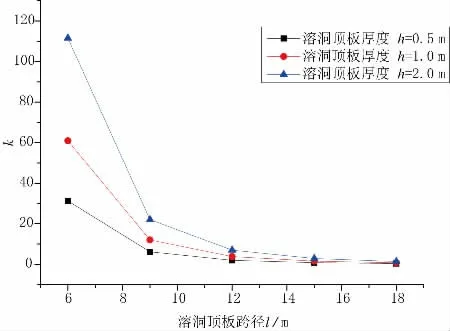
图5 溶洞顶板跨径影响分析

通过图5 可知，随着溶洞顶板跨径的增大，无量纲参量k 随之减小，当溶洞顶板跨径达到某一临界跨度时，k 将由大于1 的值变化到小于1 的值，此时顶板也将发生失稳。如当溶洞顶板厚度为1.0 m 时，此时溶洞顶板的失稳的临界跨径约为17.1 m。

3.4.3 溶洞顶板失高的影响分析

为探究溶洞顶板失高对其稳定性的影响，令q=100 MPa，E=19 GPa，l=15 m，h 为0.5 m、1.0 m、2.0 m，并使溶洞顶板失高f 分别为2 m、3 m、4 m、5 m、6 m时，代入式（25）可得，溶洞顶板失高f 对k 的影响，见图6。

通过图6 可知，随着溶洞顶板失高的增大，无量纲参量k 随之增加。说明当溶洞顶板跨径一定时，随着溶洞失高与跨径比值的增加，溶洞顶板的拱效应越强，溶洞顶板的极限承载力也越高。

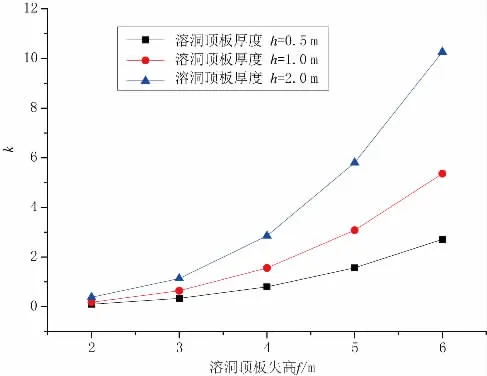
图6 溶洞顶板失高影响分析

3.4.4 岩层的弹性模量的影响分析

为探究岩层弹性模量对溶洞顶板稳定性的影响，令q=100 MPa，l=15 m，f=4 m，h 为0.5 m、1.0 m、2.0 m，并使岩层的弹性模量E 分别为17 GPa、19 GPa、21 GPa、23 GPa、25 GPa 时，代入式（25）可得，岩层弹性模量E对k 的影响，见图7。

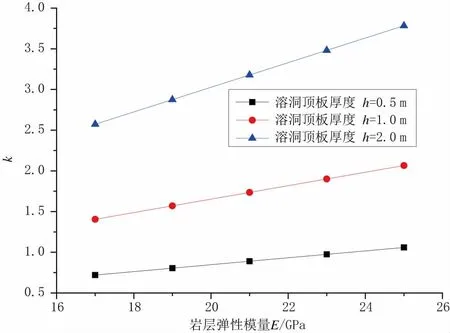
图7 岩层弹性模量影响分析

通过图7 可知，随着岩层弹性模量的增加，无量纲参量k 呈线性递增，说明溶洞顶板的极限承载力与岩层弹性模量正相关。

3.4.5 溶洞顶板上覆荷载的影响分析

为探究溶洞顶板上覆荷载对其稳定性的影响，令E=19 GPa，l=15 m，f=4 m，h 为0.5 m、1.0 m、2.0 m，并使溶洞顶板上覆荷载q 分别为50 MPa、100 MPa、150 MPa、200 MPa、250 MPa 时，代入式（25）可得，溶洞顶板上覆荷载q 对k 的影响，见图8。

通过图8 可知，随着溶洞顶板上覆荷载的增加，无量纲参量k 呈非线性递增，说明溶洞顶板的极限承载力与溶洞顶板上覆荷载负相关。

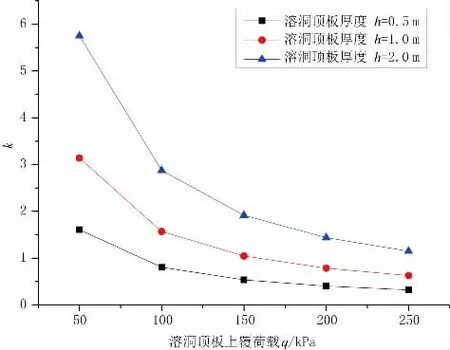
图8 溶洞顶板上覆荷载影响分析

4 结论

（1）根据路基下伏溶洞受荷体系的力学特性，将结构体系简化为两端固定铰支的扁拱模型，其受力特点更加符合工程实际。

（2）基于扁拱突变理论推导出路基下伏溶洞顶板的极限承载力及最小安全厚度，该方法可综合分析溶洞自身各参数及其上覆荷载对顶板稳定性的影响。

（3）溶洞顶板的极限承载力随着溶洞顶板厚度h的增加，溶洞顶板失高f 的增加、岩层弹性模量E 的增加而增加，随着溶洞顶板跨径l、溶洞顶板上覆荷载q 的增加而减小。