上海市简支小箱梁桥面板窄湿接缝研究分析

戚泽远

[同济大学建筑设计研究院（集团）有限公司，上海市 200092]

0 引言

随着城市建设的不断发展，城市高架桥梁越来越多，对桥梁施工阶段的要求也越来越严格。城市桥梁所处位置环境复杂，部分桥梁施工环境要求比较高，需要交通绕行甚至中断交通，这大大降低了道路的通行能力，影响城市交通系统的正常运营。

尽量减少高空作业，降低现场焊接和浇筑工作量，是现代桥梁预制拼装技术的发展趋势。预制拼装桥梁有着现场环境要求低、施工工期短、施工期交通影响小、环境污染少等诸多优点，正逐渐成为城市高架桥梁的首选结构。

简支预应力混凝土小箱梁是上海市常用的预制拼装结构。该结构受力清晰、抗扭能力强、施工较方便，已大规模应用于上海市多个工程中。但是小箱梁现浇湿接缝的宽度较宽，为0.5～1.6 m，仍需要一定的现场焊接工作量，有高空作业风险。

本文以上海市某越江大桥引桥为工程背景，通过计算简支预应力混凝土小箱梁桥面板窄湿接缝的受力情况，分析无焊接湿接缝的受力性能，用于指导设计。

1 工程概况

上海市某越江大桥引桥的桥梁结构采用上海市简支预应力混凝土小箱梁结构，桥面全宽13 m，结构净宽12.7 m，布置3 道小箱梁。桥梁所在道路为二级公路，设计车道荷载等级为公路-II 级。

引桥小箱梁标准跨径35 m，梁高1.9 m。按常规小箱梁湿接缝做法，湿接缝宽1.611 m，厚0.2 m，如图1 所示；按窄湿接缝做法，窄缝下口宽0.3 m，上口宽0.35 m，厚0.25 m，如图2 所示。

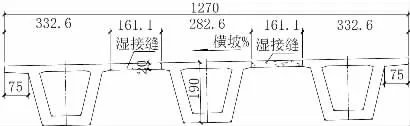
图1 引桥小箱梁常规湿接缝做法断面（单位：cm）

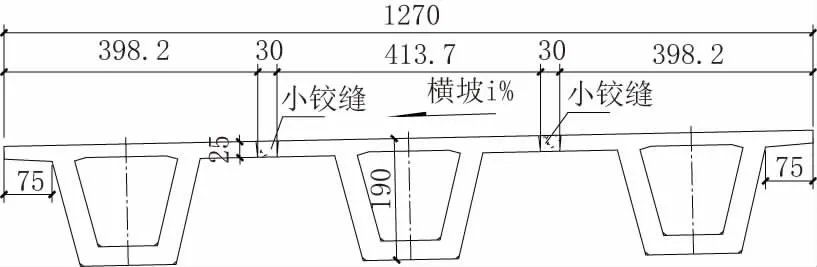
图2 引桥小箱梁窄湿接缝做法断面（单位：cm）

常规湿接缝做法需要焊接圈筋，圈筋与两侧小箱梁预留钢筋焊接，焊接长度要满足双面焊5 d、单面焊10 d[1]的要求。此时可认为两侧小箱梁钢筋贯通湿接缝，按单根通长钢筋计算，如图3 所示。

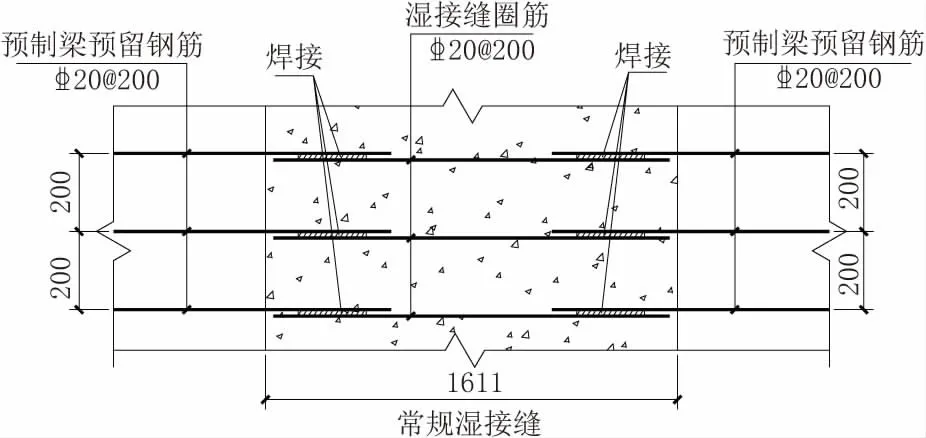
图3 引桥小箱梁常规湿接缝做法平面配筋（单位：mm）

窄湿接缝做法由于铰缝比较窄，采用两侧U 形钢筋铰接、内穿横向栓筋的构造，无须现场焊接钢筋，施工时仅需错开两侧小箱梁的预留钢筋即可，如图4 所示。

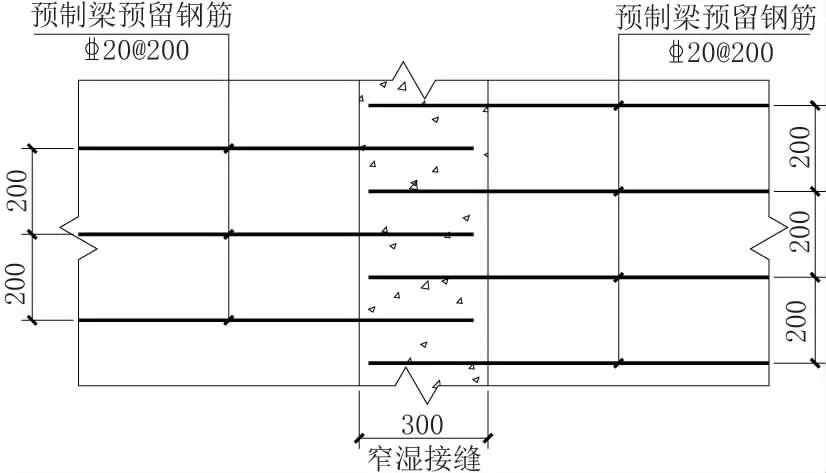
图4 引桥小箱梁窄湿接缝做法平面配筋（单位：mm）

2 桥面板常规算法

2.1 计算模型

常规湿接缝内的圈筋与两侧小箱梁预留钢筋焊接，计算时可认为两侧小箱梁钢筋贯通湿接缝，按单根通长钢筋计算。

桥面板上下缘横向配筋均为D20@200 mm，受力钢筋的净保护层厚度为30 mm。常规湿接缝桥面板计算取箱梁跨中断面（腹板、底板最薄处），按钢筋混凝土构件进行验算。单元的纵向宽度取1 m，采用桥梁博士V3.6 建立小箱梁横向杆系计算模型。计算模型如图5 所示。

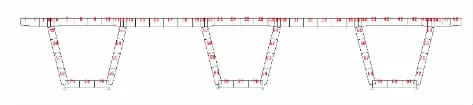
图5 常规湿接缝小箱梁桥面板计算模型（单位：mm）

车辆荷载按《公路桥涵设计通用规范》（JTG D60—2015）[2]的规定公路一级车辆荷载考虑。d=1.4 m，a1=0.2 m，单轮轴重140 kN，双轮轴重2×140 kN。桥面板车轮荷载分布宽度根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3363—2018）[1]第4.2 节计算。计算时，桥面铺装厚度取0.18 m。

2.2 计算结果

强度验算结果如图6 和图7 所示。

图6 承载能力极限状态最大抗力及对应的内力（单位：kN·m）

图7 承载能力极限状态最小抗力及对应的内力（单位：kN·m）

常规湿接缝桥面板配筋的强度满足要求。

桥面板上、下缘裂缝验算结果如图8 所示。

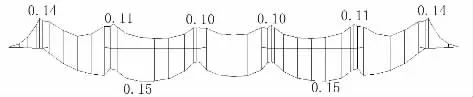
图8 正常使用极限状态频遇组合上、下缘裂缝宽度（单位：mm）

常规湿接缝桥面板的上、下缘裂缝宽度最大为0.15 mm，位于湿接缝下缘，小于《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3362－2018）[1]中第6.4.2 条规定的0.2 mm，满足要求。

窄湿接缝桥面板的构造为两侧U 形筋铰接、中间横穿栓筋的做法。此类构造因为两侧U 形钢筋没有焊接，减少了许多现场作业，但是湿接缝处无法用杆单元模型模拟。

3 桥面板实体模型计算

3.1 实体模型

桥面板实体模型采用分离式有限元模型。分离式有限元模型把钢筋和混凝土作为不同的单元来处理，即混凝土采用三维非线性实体单元Solid65，钢筋采用Link8 杆单元[3]。

以单跨简支梁模拟湿接缝受力状态，以湿接缝两侧小箱梁腹板中心线之间的距离作为简支梁跨径，桥面板纵桥向计算宽度取1 m。计算取车辆轮载分布宽度1 m，分布长度0.6 m，如图9 所示。

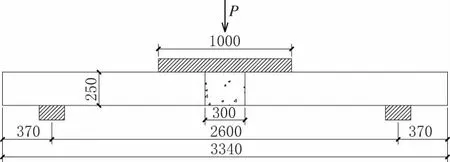
图9 实体模型荷载布置示意图（单位：mm）

创建模型时，将几何实体以钢筋位置切分，分离式有限元模型将钢筋的具体布置按实际情况建出，其计算结果更加符合实际。模型假定湿接缝足够密实，新旧混凝土结合状态良好，不考虑钢筋在混凝土之间的滑移，实体模型如图10 所示。

图10 引桥小箱梁湿接缝实体计算模型

3.2 材料性质

材料性质采用《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3363—2018）[1]中的强度设计值（见表1）。

表1 混凝土材料参数

混凝土单轴应力-应变关系曲线采用多线性等向强化模型MISO 模拟，曲线上升段按《混凝土结构设计规范》（GB 50010—2010）[4]规定的公式输入。其中，混凝土曲线的ε0=0.002，εcu=0.003 3，因无法模拟下降段，下降段采用平直段计算。

混凝土破坏过程采用Willam-Warnker 5 参数破坏准则[3]。张开裂缝的剪力传递系数βt=0.5，闭合裂缝的剪力传递系数βc=0.95，拉应力释放系数采用缺省值Tc=0.6，其余参数取程序默认值。

材料的应力-应变关系曲线如图11 所示。

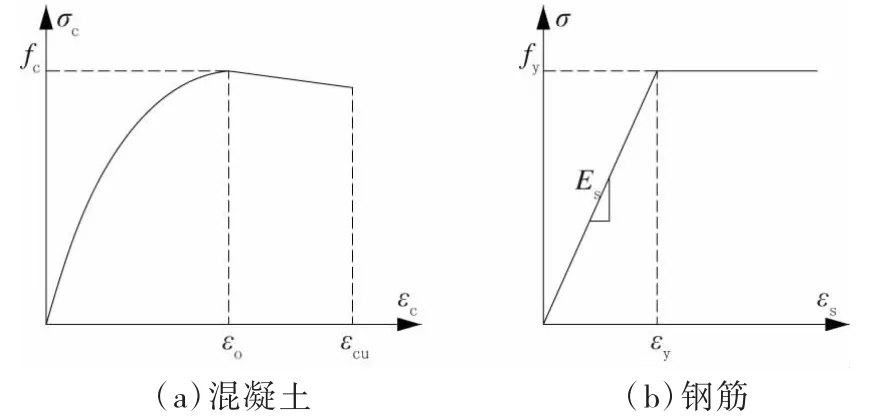
图11 材料的应力-应变曲线

钢筋的应力-应变关系可采用理想弹塑性模型。本工程采用双线性等向强化模型BISO 模拟，钢筋材料参数见表2。

表2 钢筋材料参数

3.3 单元划分与计算方法

为分析湿接缝不同构造的受力情况，分为3 个模型进行计算，分别为：

模型A：窄湿接缝计算模型；

模型B：常规湿接缝计算模型；

模型C：少横栓的窄湿接缝计算模型。

同时，为提高计算精度、降低应力集中对计算结果的影响，模型的钢筋、混凝土单元采用映射划分，划分尺寸取50 mm。计算模型钢筋分布和划分如图12 所示。

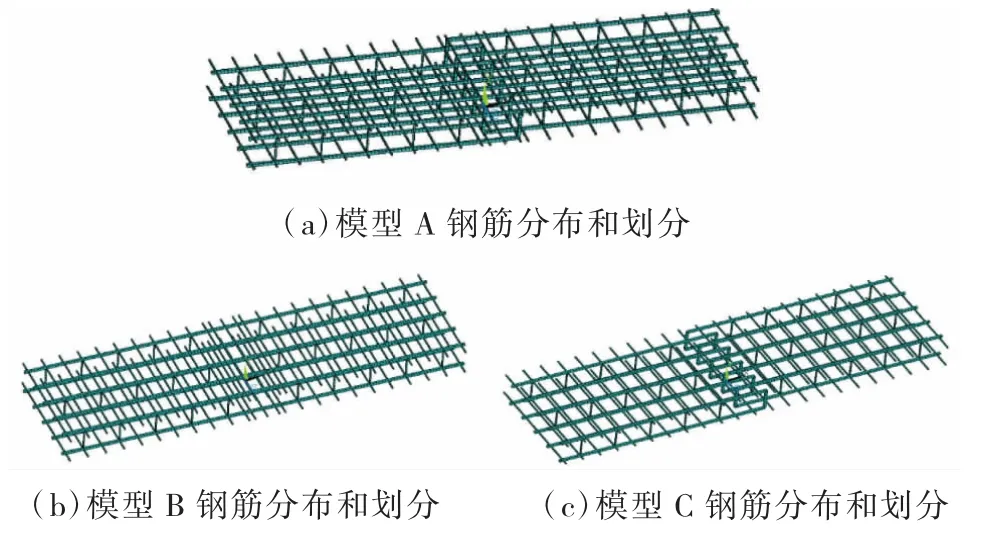
图12 计算模型钢筋分布和划分

计算采用面加载的方式，受力范围为0.6×1.0 m。子步数为100，每个荷载的子步的迭代次数为50。静力加载，采用位移收敛准则，收敛误差取2%。

模型计算采用单调静力加载，不计桥面板自重，通过多次重复计算求得极限荷载，以极限荷载对比分析不同模型的受力承载力[5]。计算主要过程如下：

（1）根据规范中抗弯构件承载力计算公式，求得常规湿接缝桥面板的极限弯矩为98.5 kN·m，跨中集中荷载的理论极限荷载为151.5kN。

（2）以理论极限荷载151.5 kN 为基础，多次施加大于理论极限荷载的竖向荷载进行计算。若计算收敛，则增加荷载重新计算，直至不收敛为止。以不收敛的上一级荷载为收敛荷载。

（3）在上一阶段的收敛荷载基础上，以0.1 kN 为最小荷载增量，多次计算，求得最大收敛荷载。以最终计算的最大收敛荷载为模型的极限荷载。

3.4 计算结果与分析

实体模型中的钢筋本构关系为理想双线性BISO模型，而混凝土的本构关系模型却无法模拟下降段。模型计算时的不收敛是由于钢筋受拉屈服后引起屈服段钢筋单元节点位置迅速发展导致的，因此模型计算得到的极限荷载对应的即受拉筋的屈服荷载。

实体模型A、模型B计算所得的竖向集中力-跨中挠度关系曲线对比如图13 所示。

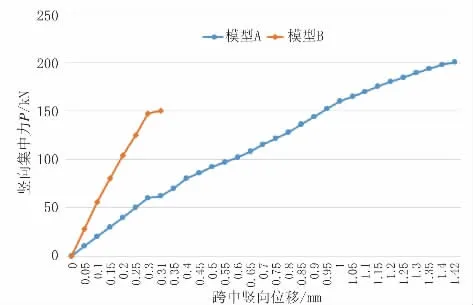
图13 模型A、模型B计算结果对比

模型B 为常规湿接缝构造，极限荷载为150.1 kN，与理论计算值151.5 kN 接近，差值在1%左右，说明实体计算结果与理论计算结果基本一致。

模型A 为窄湿接缝构造，极限荷载为200.2 kN，是极限荷载理论计算值的1.32 倍。这表明，在保证混凝土密实、新旧混凝土结合稳固、钢筋与混凝土无滑移的条件下，混凝土窄湿接缝的U 形筋铰接构造比一般常规湿接缝做法更可靠，可以保证桥面板的承载力。

实体模型A、模型C 为窄湿接缝的不同钢筋构造，其计算所得的竖向集中力-跨中挠度关系曲线对比如图14 所示。

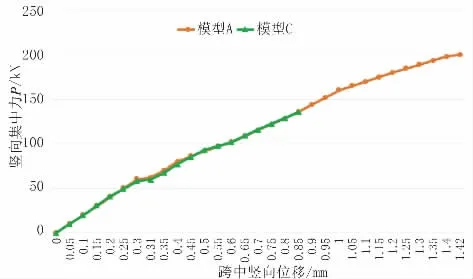
图14 模型A、模型C计算结果对比

模型C 为少横栓窄湿接缝构造，其两侧U 形筋之间横栓比较少，除U 形筋角点处外，内侧没有设置横向钢筋。

计算结果显示，模型C 的竖向集中力-跨中挠度关系曲线与模型A 的前半段基本一致，但是模型C 的极限荷载仅为135.5 kN，是设置横栓钢筋的模型A 极限荷载的0.68 倍。这说明，在窄湿接缝的U形钢筋铰接构造中，横向栓筋的加强作用特别明显，可以显著提高湿接缝的承载力。

另外，模型C 的极限荷载值也小于理论计算值，是理论计算值的0.89 倍。这更加表明横向栓筋的重要性，在少横向钢筋的情况下，窄湿接缝的U 形钢筋铰接构造是达不到常规湿接缝做法的承载力的。

实体模型A、模型B、模型C 极限荷载实体模型计算值与理论计算值见表3。

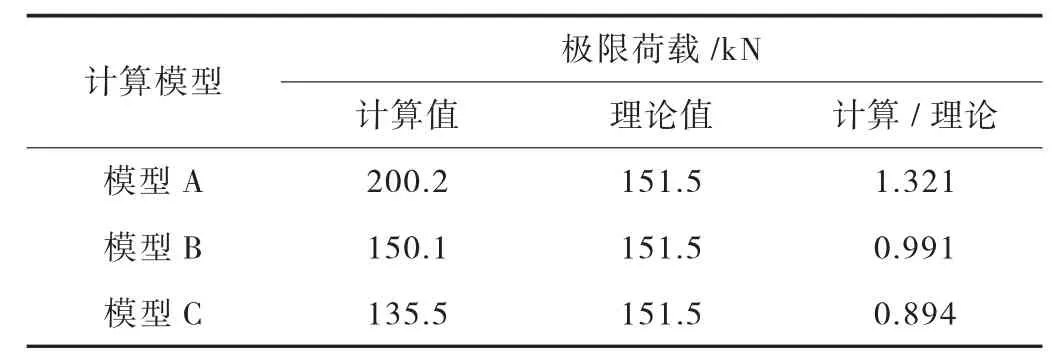
表3 极限荷载计算结果与理论值对比

4 结语

本文计算对比了窄湿接缝与常规湿接缝的构造和受力情况，主要得到以下结论：

（1）窄湿接缝的U 形钢筋铰接构造无法用杆单元模拟，可用实体单元模型进行计算。

（2）在保证混凝土密实、新旧混凝土结合稳固、钢筋与混凝土无滑移的情况下，混凝土窄湿接缝的U形筋铰接构造比一般常规湿接缝做法更可靠，可以保证桥面板的承载力。

（3）在窄湿接缝的U 形钢筋铰接构造中，横向栓筋的加强作用特别明显，可以显著提高湿接缝的承载力。若不设横向栓筋，湿接缝承载力比常规做法要小。