基于亚像素图像平移叠加提高大倾角同步卫星信噪比的方法研究

欧阳旖旎 罗 浩 唐正宏 李 岩 王 瑞

(1 中国科学院上海天文台上海 200030)

(2 上海大学通信与信息工程学院上海 201900)

(3 中国科学院大学北京 100049)

1 引言

地球同步轨道(GEO)为中心距离地心42164 km,径向宽度400 km,轨道倾角小于15◦的环状区域,如图1所示.地球同步轨道卫星周期与方向和地球自转的周期与方向相同,因此其角速度等于地球自转的角速度,所以卫星能够实现对地面同一区域连续观测.当同步卫星轨道倾角为0◦时,其相对地面静止.当同步卫星轨道倾角不为0◦时,其星下点做南北方向的“8”字周期运动,倾角越大,运动范围越大[1].

随着各国卫星发射活动的增加,地球同步轨道带中的GEO目标越来越多,其中正在工作的同步卫星是全部GEO目标的1/3.为了保证国防与航天安全,防止工作的同步卫星与碎片或废弃卫星相撞,需要对我国上空的GEO目标进行严密监测.根据2018年3月7日北美空防司令部(North American Aerospace Defense Command,NORAD)发布的卫星根数信息统计,目前在轨的约1100颗GEO目标中仅有约35%的目标轨道倾角接近0◦,超过50%的GEO目标轨道倾角大于5◦,图2是GEO目标轨道倾角统计情况.

由于多种摄动因素的影响,倾角不为0◦的GEO目标相对地面并非绝对静止,存在东西向与南北向的漂移,其星下点做南北向(纬度)的“8”字运动,运动范围、速度与轨道倾角有关,不同轨道倾角GEO目标在不同位置的运动速度如图3所示.

为了对地球同步轨道空间进行动态监测,上海天文台在云南丽江高美古观测站安装了最新研制的地球同步轨道动态监视系统,简称FocusGEO系统.该系统仅需要赤经轴的运动就可对台站上空的地球同步轨道带进行不间断的扫描观测,从而得到同步轨道带的全幅动态宏观场景,实现对同步轨道空间目标的编目管理和动态监测.FocusGEO系统视场为300 deg2,探测星等为15等(曝光5 s),覆盖范围为东西方向±60◦,南北方向±15◦.在常规观测时,为了能通过帧间关联提取GEO目标星象,FocusGEO系统一般对每个天区都连续曝光10次[2].

由于距离和太阳相位角的变化,有些小尺寸GEO目标有时候比较暗弱,为了提升系统的探测能力,需要采用适当手段来提高目标的信噪比.孙荣煜等[3]提出叠加连续多帧图像的方法提高目标的信噪比,取得了较好的效果.值得指出的是,上述方法仅适用于轨道倾角接近于0◦的GEO目标.对于轨道倾角较大的GEO目标,由于目标相对地面观测者存在一定的角速度,其在相邻观测图像中的位置并不重合,叠加时目标的信号无法累加,因此不能提高目标的信噪比.借鉴王斌等[4–5]在探测暗弱小行星时采用的图像位移叠加的方法,本文进一步提出亚像素平移错位叠加连续多帧CCD图像的方法,这样可以使得叠加过程中目标信号有效累积,从而可以提高目标的信噪比,更有利于探测暗弱的目标.

本文首先从原理上分析了图像平移叠加对运动目标信噪比的影响,然后介绍了图像平移叠加的方法及流程,最后通过对不同运动速度GEO目标的实测图像进行叠加试验,分析比较叠加前后目标的信噪比,验证了通过平移叠加图像提高运动GEO目标信噪比的可行性和实际效果.

2 基本原理

2.1 信噪比计算

一颗星象在一个方向上的信号强度示意图如图4所示,其中B是背景均值,δ是背景的噪声起伏,Imax是星象峰值.信噪比(SNR)是星象本身信号与噪声的比,其中噪声主要由两部分组成:一是星象本身产生的噪声,该部分通常认为服从泊松分布,二是背景噪声产生的起伏[6].

根据具体的使用环境和要求,有3种不同的信噪比定义方式[7],针对本文中的星象情况,采用的信噪比计算公式为:

2.2 叠加原理

在已知目标的轨道倾角和运动速度的情况下,根据CCD相机多次曝光的时间间隔和CCD相机单位像素的空间张角,可以计算出目标在CCD序列图像上移动的像素数.根据目标的运动方向,平移相应的像素数,使GEO目标星象在所有观测图像上的位置基本重合,然后叠加多帧图像,图像叠加对目标信号的增加大于噪声的增加,从而提高目标的信噪比.

设一组观测图像共n幅,其中第1幅图像为f1(i,j),第n幅图像为fn(i,j),i、j表示图像中像素的坐标.叠加时,以第1幅图像为参考基准,若目标在相邻图像之间的平移量为m像素,则第2幅图像平移m个像素,第3幅图像平移2m个像素,依此类推,第10幅图像平移9m个像素,平移后的新图像分别为=f1(i,j),则叠加图像f(i,j)为:

2.2.1 整数像素平移

设每幅图像大小为M ×M,则第n幅图像fn(i,j)中1 ≤i≤M,1 ≤j≤M,平移后图像为.平移像素数m需满足0 ≤m≤M,若目标运动方向向左,以第1幅图像为基准,则平移后的第2幅图像为:

平移后的第n幅图像为为:

若目标运动方向向右,以第1幅图像为基准,则平移后的第2幅图像为:

平移后的第n幅图像为为:

图5为3幅5×5的图像向右平移1个像素以及向左平移1个像素的示意图,其中x、y、z表示每幅图像的像素值.

2.2.2 亚像素平移

设平移量为∆,平移参数x1为⎿|∆|」,其物理含义是平移的整数像素部分,平移参数x2为|∆|−x1,其物理含义是平移的亚像素部分.若∆大于0,即目标运动方向向左时,若x1=0,则平移后的第2幅图像为:

如图6 (a)所示.若x1>0,则平移后的第2幅图像为:

如图6 (b)所示.若∆小于0,即目标运动方向向右时,若x1=0,则平移后的第2幅图像为:

如图6 (c)所示.若x1>0,则平移后的第2幅图像为:

如图6 (d)所示.其余图像依此类推,设相邻两幅图像的平移像素为∆x,以第1幅图像为基准,第n幅图像的平移量为∆n,则第n幅图像的平移量∆n=∆x(n−1).最后将第1幅图像与其余n−1幅平移后新图像叠加,再除以n,得到平移叠加后的图像.

2.3 模拟仿真

在理想情况下,叠加n幅图像时,根据前文的信噪比计算公式,单幅图像的信噪比为SNR=,因此叠加图像的信噪比为SNR=,可知叠加图像的信噪比是原图像信噪比的倍.在实际情况下,由于CCD读出噪声的影响,叠加图像的信噪比与原图像信噪比相比,会略低于倍.

3 实验方法

本次实验采用了FocusGEO分别在丽江和佘山的观测图像.望远镜指向固定天区,采用凝视观测模式,曝光间隔为6–10 s.视场内的GEO目标星象基本呈圆形,而恒星星象为拖长星象.采用连通域方法识别目标星象,确定目标所在区域,然后用2维修正矩定心法计算星象位置坐标.该方法用一个高于实际背景的门限水平消除掉背景的影响,在星象中心定位过程中,只考虑高于此门限的数据,即:设T=B+3δ,图像大小为N × N,0 ≤i≤N,0 ≤j≤N,

则矩公式为:

其中I′(i,j)为消除背景后的图像,I(i,j)表示原图像,i0、j0为星象中心坐标.根据前文的信噪比计算公式,在一组观测图像中,分别计算单幅图像中目标的信噪比以及叠加图像中目标的信噪比,通过信噪比的比较来验证信噪比的提升.

4 实测图像叠加

样本1为2017年12月24日UTC 15:04:46–15:06:32的一组观测图像,其曝光间隔为6 s,如图7所示.样本2为2017年12月24日UTC 16:47:09–16:48:55的一组观测图像,其曝光间隔为10 s,如图8所示.

4.1 计算平移量

在样本1中,第1幅图像如图7 (a)所示,目标在图像中的位置坐标为i:1281.80,j:968.30,信噪比为20.9.第10幅图像如图7(c)所示,目标在图像中的位置坐标为i:1293.65,j:967.91,信噪比为21.0.比较图7 (b)和图7 (c)中目标的位置,可知目标在x正方向上运动了11.85个像素,相邻图像间目标运动了1.32个像素,整数像素平移叠加时的平移量为1 pixel,亚像素平移叠加时的平移量为1.3 pixel.

在样本2中,第1幅图像如图8 (b)所示,目标在图像中的位置坐标为i:557.00,j:694.30,信噪比为26.4.第10幅图像如图8 (c)所示,目标在图像中的位置坐标为i:561.54,j:695.43,信噪比为52.2.比较两幅图像中目标的位置,可知目标在x正方向上运动了4.54个像素,相邻图像间目标的平移像素数为0.5 pixel.整数像素平移叠加时的平移量为1 pixel,亚像素平移叠加时的平移量为0.5 pixel.

4.2 平移叠加图像

本次实验按图像的观测顺序,将10幅图像分为6组连续图像,即第1幅图像至第5幅图像为一组,第2幅图像至第6幅图像为一组,以此类推,分别错位叠加每一组的5幅图像.如图9所示为样本1的6幅整数像素叠加图像,如图10所示为样本1的6幅亚像素叠加图像.图11所示为样本2的6幅亚像素叠加图像.图12所示为样本2的6幅整数像素叠加图像.

4.3 叠加效果

如图9–12所示,错位叠加图像中,目标星象依然为圆形星象,其余星象均为拖长星象.对于样本1,其整数像素叠加图像与原图像的信噪比如表1所示,其亚像素叠加图像与原图像的信噪比如表2所示.

表1 样本1原图像与整数像素叠加图像的信噪比Table 1 The SNR of sample 1 between original image and composition image with integral pixel

表2 样本1原图像与亚像素叠加图像的信噪比Table 2 The SNR of sample 1 between original image and composition image with sub-pixel

对于样本2,其整数像素叠加图像与原图像的信噪比如表3所示,其亚像素叠加图像与原图像的信噪比如表4所示.样本1的10幅观测图像中目标的信噪比平均值为22.1,6幅整数像素叠加图像中目标的信噪比平均值为39.4,6幅亚像素叠加图像中目标的信噪比平均值为43.8.叠加后,目标的信噪比有了显著提升,其中整数像素叠加时,目标信噪比提升了78%,亚像素叠加时目标信噪比提升了98%.表5为样本1与样本2亚像素叠加图像与整数像素叠加图像的半峰全宽(FWHM).星象的半最大全宽即星象峰值的一半处的星象宽度,将图像在MaxIm Dl软件中打开,可直接查看星象的半最大全宽.

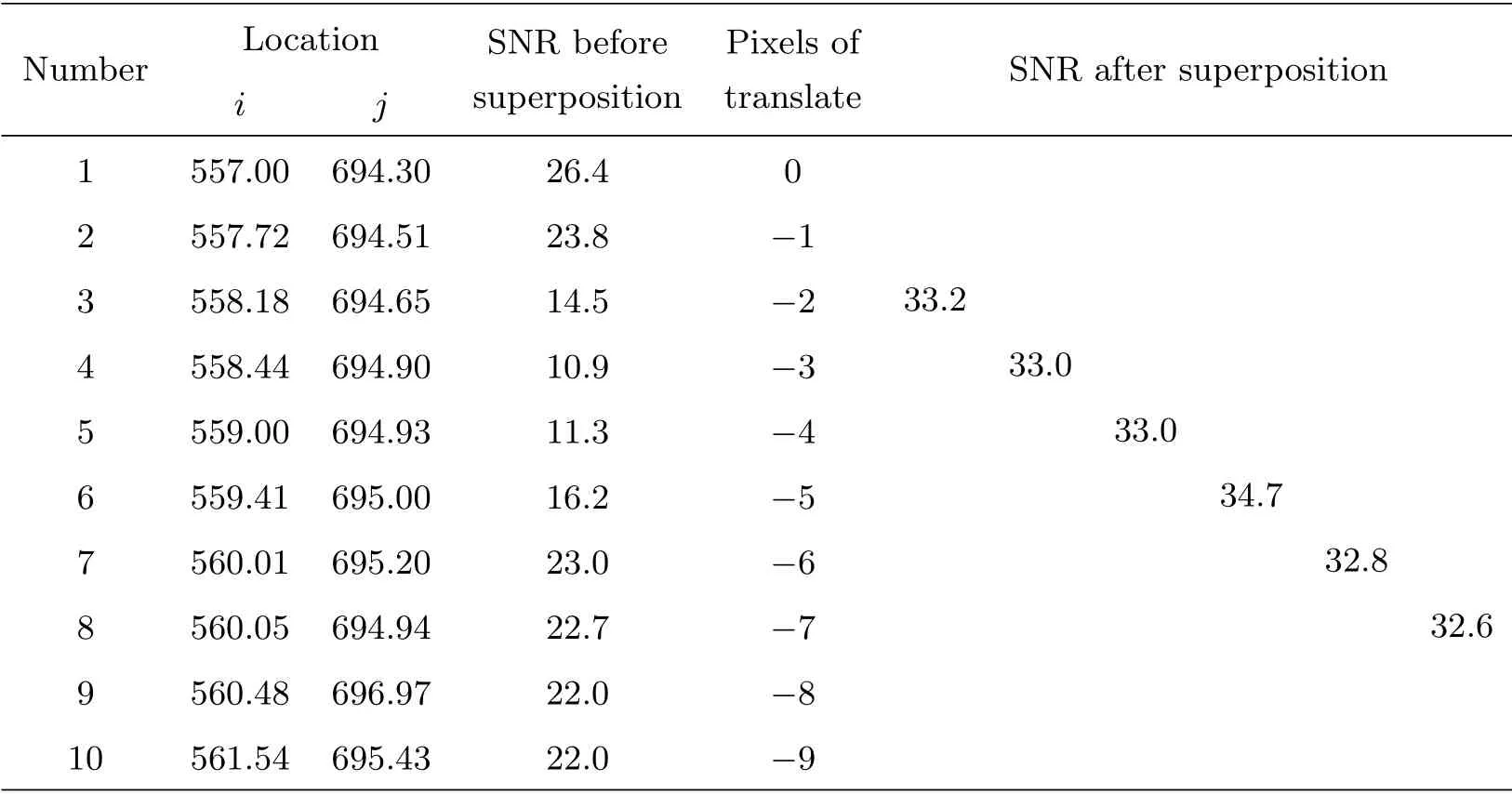
表3 样本2原图像与整数像素叠加图像的信噪比Table 3 The SNR of sample 2 between original image and composition image with integral pixel

表4 样本2原图像与亚像素叠加图像的信噪比Table 4 The SNR of sample 2 between original image and composition image with sub-pixel

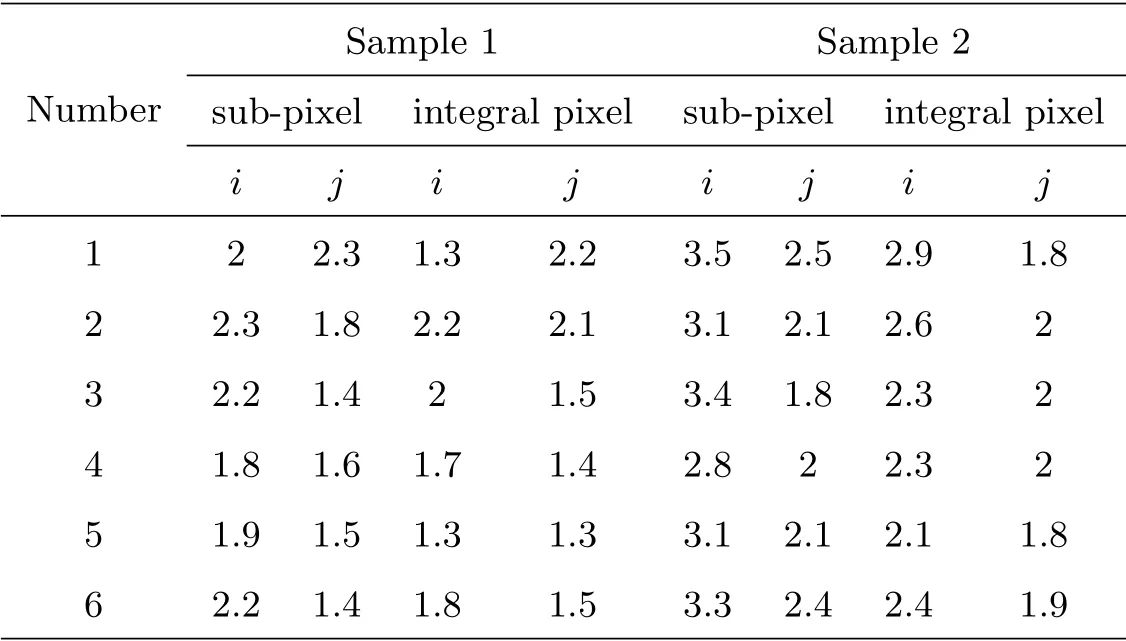
表5 样本1与样本2亚像素叠加图像与整数像素叠加图像的半峰全宽Table 5 The FWHM of sample 1 and sample 2 between composition image with sub-pixel and composition image with integral pixel

样本2的10幅观测图像中目标的信噪比平均值为19.3,6幅整数像素叠加图像中目标的信噪比平均值为33.2,6幅亚像素叠加图像中目标的信噪比平均值为39.6.整数像素叠加时,目标信噪比提升了72%,亚像素叠加时,目标信噪比提升了105%.

5 目标移动速度未知情况下的枚举法叠加

对于一些因信噪比较低而无法在单帧图像中被检测到的暗弱目标,根据先验信息,该天区可能存在目标,可以通过平移量的连续枚举方式分别叠加连续观测图像.当枚举到接近目标实际运动速度时,目标的信噪比提高会比较明显,从而被目标检测算法检测到.本文选取了一组10幅连续观测图像,其第1幅图像如图13所示.该视场中可能有一颗目标,单帧图像未能检测出来.对这10幅图像分别以平移量0.2、0.4、0.6、0.8、1.0像素叠加.图14为不同平移量的叠加图像,平移0.2像素后软件可以检测出一个目标,信噪比为4.7;其他平移量叠加后的目标信噪比如表6所示.

由表6可知,当平移量为0.6像素时信噪比最高.为了确认,再分别以平移量0.5像素、0.7像素进行叠加.叠加图像如图15所示.平移量为0.5像素时,目标信噪比为9.44,平移量为0.7像素时,目标信噪比为8.62,由此可知最佳平移量为0.6像素,即目标以这个速度在移动.将观测图像以平移量0.6像素叠加后,检测到一个GEO目标,该目标的TLE (两行轨道数据)号为20836,是一个火箭残骸,倾角为6.2◦,星下点位置为102◦E.

表6 不同平移量的叠加图像信噪比Table 6 The SNR of composition images with different translation amounts

需要指出的是,由于目标运动存在方向性,因此枚举法平移叠加还要考虑朝另一个方向运动的情况,即平移量为−0.2、−0.4、−0.6、−0.8、−1.0像素.

枚举法平移叠加的好处是,不管目标实际运动速度多大,只要在视场中,通过枚举的方式分别叠加连续观测图像,总能找到视场中的目标(前提是叠加后该目标的信噪比要大于3).当然,这样做需要一定的计算量.好在平移叠加都是加减乘除这样的简单计算,因此计算也不需要很长时间.

6 结论

本文研究了利用平移叠加连续观测图像,以提高GEO运动目标信噪比的方法.通过叠加FocusGEO的实测图像,目标的信噪比有了显著提升,且亚像素叠加时信噪比提升得更大,验证了平移叠加方法的有效性.叠加5幅图像时整数像素叠加图像的信噪比是原图像的1.7倍左右,亚像素叠加图像的信噪比是原图像的2倍左右.对单帧图像中未检测到的暗弱目标,尽管不知道它的运动特征,但可以通过平移不同的像素数(枚举法)进行叠加,总能发现暗弱的未知目标.除了GEO目标外,本方法还可用于其他运动目标的图像叠加.

由于GEO目标只有垂直于赤道的运动,因此只需要在一个方向上进行叠加.对其他目标,其运动速度可能在任意方向,则需要在不同方向上进行叠加,具体的处理过程跟一个方向平移叠加类似.