风速影响下羽绒服保暖性能定量研究

张梦妮，骆鑫荣，陈少伟，屠乐希，沈 华，4

(1.东华大学纺织学院，上海201620；2.浙江中纺标检验有限公司，浙江绍兴312000；3.艾莱依时尚股份有限公司，上海200333；4.东华大学纺织面料技术教育部重点实验室，上海201620)

0 引言

羽绒服具有轻、软、蓬松、舒适等特性，赢得了无数消费者的青睐。羽绒服的热舒适性是企业设计生产羽绒服和消费者选购羽绒服的重要因素之一。作为人体与环境的媒介，羽绒服影响着人体与环境的热传递。热阻是评价羽绒服热舒适性主要度量指标，包括服装表面空气层热阻和服装固有热阻，大小主要取决于服装本身，如填充量[1－2]、含绒率[3]及面料[4]，同时受外界环境和穿着方式等多种因素影响[5]。在运动过程中风的存在会对人体穿着羽绒服的热舒适性产生一定的影响。因此，开展羽绒服热舒适性研究有助于企业设计羽绒服保暖性，满足消费者热舒适性需求。

热阻作为评价服装热舒适性的主要指标，其测试在国内外已有较多研究。ISO标准[6－7]和ASTM F1291－2016标准[8]对服装热阻的测试进行了详细的说明，此类标准要求实验时的温差均大于12℃。为了保证各研究具有可对比性，环境温度一般设置为21℃，这与羽绒服的实际穿着环境有较大的区别。XIAOMING QIAN等[9]测试了温度20±0.3℃、湿度50±5%环境下，风速与服装热阻和湿阻的关系，结果表明随着歩速和风速的增加，服装热阻和湿阻均下降。崔鹏[10]通过暖体假人测试及多层服装系统隔热值分配公式，求得了内胆材料的隔热值，并建立了内胆材料的工程厚度与隔热值之间的关系。张文欢等[11]利用热流计法测试计算得到站立和行走状态的服装总热阻。美国标准ASTM F2732－16[12]利用暖体假人在低温下测试服装热阻，给出了2MET和4MET活动水平下，不同热阻的防寒服外套适用温度，然而该标准对测试温湿度、风速有特定要求。何雨[13]研究了填充量、温度对羽绒服保暖性的影响，发现存在临界填充量，填充量相同时，－3℃～3℃时热阻随温度升高而减小，3℃～15℃时热阻随温度升高略微增大。田水承等[14]通过出汗热板仪测试了环境温湿度及风速对消防服热舒适性的影响，结果表明风速与服装热阻呈负相关，与湿阻呈正相关。已有研究探究了填充量、人体姿势、温度、人体运动状态等对热阻的影响，但是，模拟冬季羽绒服真实的穿着环境，探究环境温度、风速多个变量对羽绒服热阻的影响较少。

本文采用暖体假人在人工气候仓模拟冬季羽绒服的穿着环境和人们的穿衣习惯，分别测量了4件不同单位填充量的羽绒服在不同环境温湿度、风速条件下的热阻；分析风速对热阻的影响以及对表面对流换热和辐射换热的影响，为羽绒服的设计、研发和选购提供指导。

1 羽绒服热舒适性试验

1.1 试样

本试验定制了4件不同单位填充量的羽绒服试样，并根据所选羽绒的蓬松度、绒子含量和填充量来确定衍缝间距。羽绒服具体参数如表1所示:

表1 羽绒服具体参数

为了使测试条件更加接近人们的穿衣习惯，在测试羽绒服热阻时搭配标准内衣(100%棉)进行测试。

1.2 试验仪器

试验仪器主要包括:LD－1型暖体假人、温湿度计、FLIR热成像仪。LD－1型暖体假人为躯干发热人台，前后身为两台独立的曲面保温仪，由上下两个热护环和中间主体试验板构成。测试过程中，试验板、保护板及底板均通过电热控制在33±0.2℃范围内并保持恒温。在距离假体表面25cm处设置4个空气层温度传感器，分别分布在假体前上、前下、后上、后下，用于测试假体周围空气温度。测试在可控制环境温湿度和风速的气候仓内进行。气候仓相对湿度稳定在40%，温度设置为10℃，测试风速分别控制为0.5m/s、1.5m/s、2.5m/s、4.0m/s、7.0m/s、10.0m/s、13.0m/s，以研究不同风速对羽绒服保暖性的影响规律。测试时设置暖体假人皮肤温度33℃，温度波动±0.2℃，设置稳定时间(非稳态传热时间)30min，测试时间10min，暖体假人预热完成进入稳定阶段，为暖体假人穿着标准内衣和羽绒服，夹持并悬挂两侧衣袖后开始进行保暖性测试。测试时暖体假人实时记录功率，并在电脑端输出功率－时间曲线。采用FLIR热成像仪采集羽绒服表面温度数据。利用温湿度计记录气候仓内的实际温度和湿度。测试结束导出数据，根据温度和功率计算热阻，最终取3次测试结果的均值。

整体服装(含表面空气层)热阻的计算公式如式(1)所示:

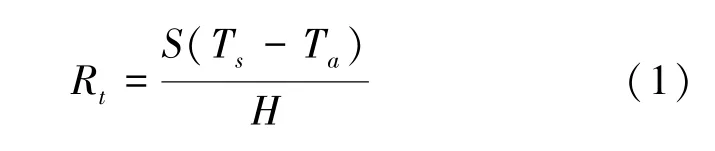
式中:Ts为稳定后“空体假人”上表面温度(℃)；Ta为空气层平均温度(℃)；S为暖体假人测试板面积(m2)；H为稳定测试阶段平均功率(W)；Rt为整体服装(含表面空气层)热阻(m2·K/W)。

服装总热阻包含服装热阻和服装表面附着的空气层热阻，由于测试时穿有标准内衣，羽绒服固有热阻如式(2)所示:

式中:R0为标准内衣的的固有热阻(m2·K/W)；Td为羽绒服表面平均温度(℃)；Rd为羽绒服固有热阻(m2·K/W)。

空气层热阻计算公式如式(3)所示:

羽绒服是通过阻止外部环境与人体之间的热交换来实现保暖。羽绒服外表面和环境温度存在温差时，会产生热对流和热辐射。服装着装后的对流换热量公式:

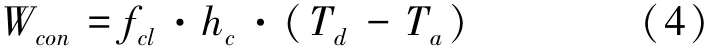
服装在合体的情况下，对流换热系数根据经验公式:

式中hc为对流换热系数，W/(m2·℃)；fcl为服装面积因子fcl＝1＋1.97Rcl；Rcl为服装固有热阻(m2·K/W)；v为风速(m/s)；Wcon为对流换热量(W/m2)。

着装后的辐射换热量:

hr的计算公式:

式中hr为辐射换热系数，W/(m2·℃)；ts为平均辐射温度(℃)；ε为服装发射率；σ为Stefan－Boltzmann常数，(5.67×10－8)w·m－1·k－4；Ar为体表面积(m2)；AD为有效辐射面积(m2)；ts为平均辐射温度(℃)；Wrad为辐射换热量(W/m2)。

2 结果与讨论

2.1 风速对服装整体热阻的影响

图1为服装整体热阻随风速变化曲线，由图1可知服装整体热阻(Rt)和风速有显著的负相关性。当测试环境为10℃，0.5m/s时，Rt分别为0.220 m2·K/W、0.246m2·K/W、0.283m2·K/W、0.339m2·K/W；

图1 服装整体热阻随风速的变化曲线

当风速上升到13.0m/s时，4种试样的Rt分别下降35.9%、30.8%、25.1%、32.9%。这是因为当风速增加时，服装表面的对流换热增大，使得人体散失的总热量增大，从而导致Rt减小。试样4的热阻最大，试样1的热阻最小，不同风速下，试样4比试样1的热阻至少大54.2%。

2.2 风速对羽绒服固有热阻的影响

图2 为羽绒服固有热阻随风速变化的曲线。由图2可知，羽绒服固有热阻(Rd)随风速的增大而减小。当风速从0.5m/s增加到13.0m/s时，试样1～4的Rd分别下降35.4%、25.7%、21.1%、33.1%。这是因为随着风速增大，羽绒服表面的风压大幅度增大，羽绒服在风压受力下被压缩，从而导致羽绒服蓬松度和内部静止空气含量降低。

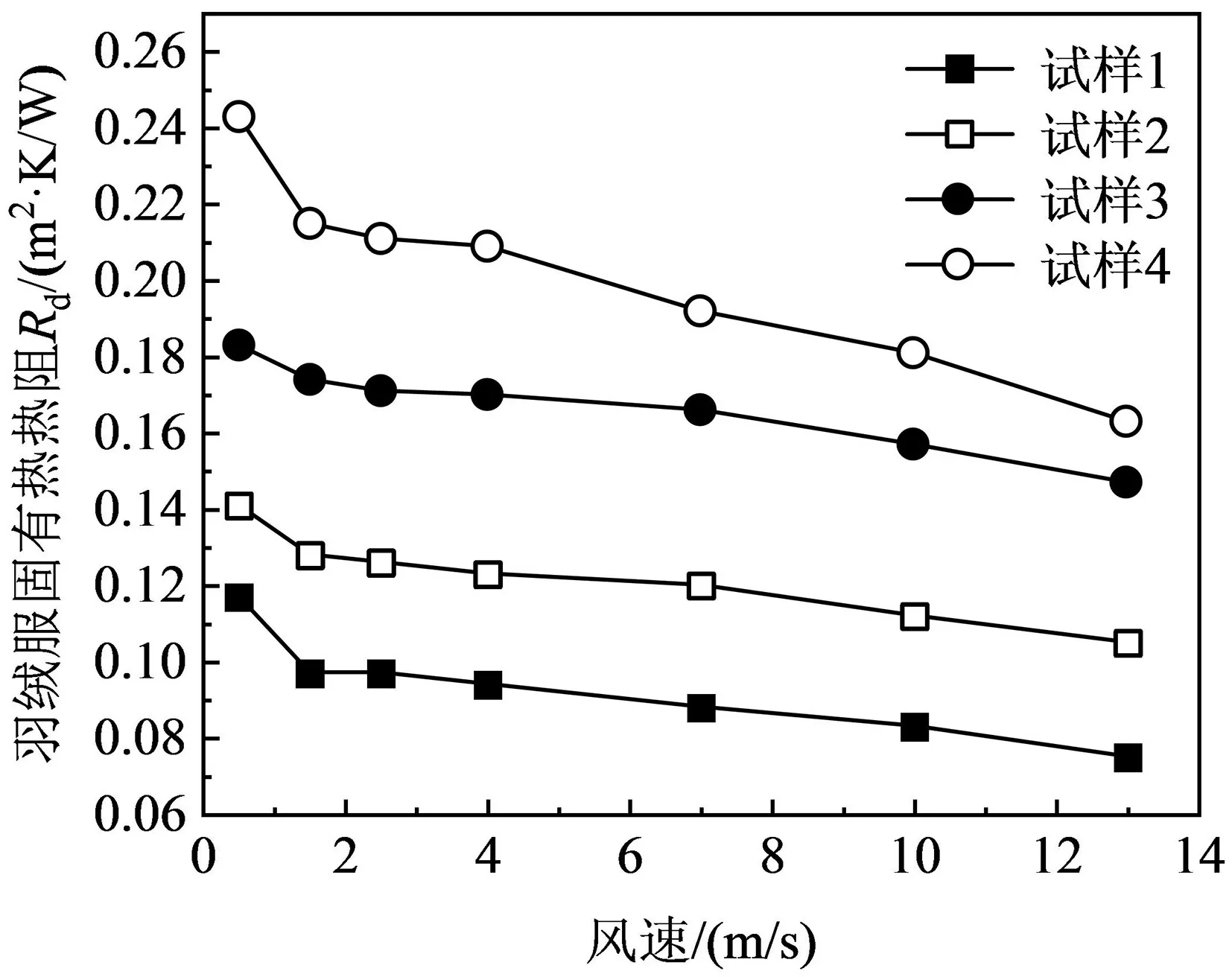
图2 羽绒服固有热阻随风速的变化曲线

由图3可知，相同风速条件下，在单位填充量为50g/m2～140g/m2范围内，Rd随着羽绒服单位填充量的增大而增大。风速0.5m/s时，单位填充量每增大30 g/m2，羽绒服热阻增幅在30%左右。这是由于随着填充量增加，单位体积内羽绒纤维数量增多，绒朵间孔隙率减小，空气流动的阻力增大，绒朵内、绒朵间维持了更多的静止空气，而静止空气的导热系数远远小于纤维的导热系数[13]，使得羽绒服内部的对流传热显著降低，从而Rd增大。当风速增大到13.0m/s时在单位填充量为50g/m2～110g/m2范围内，单位填充量每增大30g/m2，羽绒服热阻增幅变化不大；而当填充料从110g/m2增大到140g/m2时，羽绒服热阻仅升高10.9%。说明在13.0m/s的风速下，填充量为140g/m2时，羽绒服由于风压作用被压缩的程度较大，导致热阻增幅下降。

图3 羽绒服固有热阻随单位填充量的变化曲线

2.3 风速对空气层热阻的影响

根据公式(3)计算得出不同风速下，羽绒服表面的空气层热阻，如图4所示。从图4中可以看出，服装表面空气层热阻(Ra)随风速增大而减小。当测试环境为0.5m/s时，Ra最大，在0.039m2·K/W～0.047m2·K/W范围内，这是因为在微风环境下(风扇关闭)，静止空气的导热系数极小，服装表面空气层在人体周围起着较好的隔热作用。当风速增大到7.0m/s时，Ra明显下降，最大降幅为75%；当风速继续增加到13.0m/s时，Ra下降较慢，最大降幅为83%；此外，在较大风速时Ra接近零值。这是因为随着外界风速增加，羽绒服表面对流换热显著增加，空气层的隔热性下降，Ra下降。当风速增大到7m/s时，此时服装表面附着的空气层已经很稀薄，继续增加风速会导致Ra趋近于零值，下降幅度减缓。

2.4 风速对服装热流密度的影响

服装热流密度与风速的变化关系如图5所示，从图5中可以看出人体穿着不同克重的羽绒服时的热流密度均随风速的增加而增加，当风速从0.5m/s增大到13.0m/s时，热流密度最大增大51.0%。这是因为随着风速的增大，服装表面的对流换热增大，使得人体散失的总热量增大。

图5 风速和总散热量的关系

服装单位填充量与风速的变化关系如图6所示，热流密度随单位填充量的增加而降低，当单位填充量增加30g/m2，热流密度至少下降6.5%。这是因为随着单位填充量的增加，服装保暖性增加，使得假人维持皮肤上表面温度在33±0.2℃需要消耗的功率减小，导致热流密度减小。

图6 单位填充量和总散热量的关系

2.5 风速对对流换热的影响

图7 为服装表面对流换热量与风速的关系，由图7可知，随着风速增加，对流换热量增加，环境风速从0.5m/s增长到1.5m/s时，对流换热量增长较快，对流换热量至少增加52.1%。这是由于随着风速增加，环境空气从自然对流转换为强迫对流，对流换热系数(hc)显著增加，使得对流换热增加。

图7 风速与对流换热量的关系

图8 为对流换热系数与风速的关系，由图8可知，随着风速增加，hc增加，当风速增大到1.5m/s时，对流换热系数较0.5m/s时增大100.5%。随着风速继续增加，hc增长幅度逐渐降低。同时，服装表面对流换热增加引起表面温度降低，服装表面温度和空气层温度的差值逐渐减小。由于对流换热量同时受对hc、Td等多个因素的综合影响，所以随着风速增加，对流散热总体呈上升趋势，在1.5m/s处上升幅度最大，之后增幅降低。

图8 风速和对流换热系数的关系

2.6 风速对辐射换热的影响

图9 为10℃环境温度条件下，辐射换热量和风速的关系曲线图。由图9可知随着风速增加，辐射换热量减小，0.5m/s～7.0m/s下降较快，7.0m/s～13.0m/s下降较慢。环境风速为7.0m/s时，辐射换热量下降75%左右，13.0m/s时下降85%左右。这是因为风速增加，服装表面温度降低，使得服装表面温度和周围环境的温度差降低，导致辐射散热量减小，如图10所示。辐射换热量下降趋势减缓是由于7.0m/s时Td已接近环境温度，服装表面与环境温差在0.84℃～1.46℃范围内，风速继续增加到13.0m/s时，温差在0.50℃～0.08℃范围内，与7.0m/s相比变化不大。

图9 风速与辐射换热量的关系

图10 风速和辐射换热系数的关系

3 结论

(1)通过实验表明，当人体静止站立时，着装后服装整体热阻、羽绒服固有热阻、空气层热阻均随风速增加而减小。环境风速为1.5m/s时服装整体热阻受风速影响较大，增加到13.0m/s服装整体热阻下降25.2%～35.9%，下降趋势减缓；羽绒服固有热阻下降21.1%～35.4%；空气层热阻下降80.0%～82.3%，0.5m/s～7.0m/s范围内下降较快，7.0m/s～13.0m/s范围内下降幅度较慢，并在较大风速时Ra接近零值。

(2)风速与服装总散热量成正相关。当环境风速从0.5.m/s增大到13.0m/s时，热流密度最大增大51.0%。

(3)对流散热量随风速增加而增大，环境风速为0.5m/s～1.5m/s，对流散热量上升幅度较大，之后上升幅度减小。辐射散热量随风速增加而减小，环境风速为0.5m/s～7.0m/s，辐射散热量下降较快，7.0m/s～13.0m/s辐射散热量下降趋势减缓。