基于历史预警准确率的时空重排扫描最大扫描半径优化方法

张 亚 楠，龙 华，邵 玉 斌，杜 庆 治，陈 腾 飞

(昆明理工大学信息工程与自动化学院，云南 昆明 650500)

0 引言

随着大数据时代的到来，通过时空数据异常探测可发现诸多重要信息。例如：识别路况中的时空异常数据，有助于检测造成交通拥堵的交通事件[1]；搜寻疾病[2]、犯罪[3]、火灾[4]、极端高温[5]等发生的热点地区，有助于分析事件发生的规律并对未来事件提出预警。为利用时空异常数据中蕴含的重要信息并挖掘其中的价值，越来越多的学者开始探索时空异常数据的探测方法[6-8]。

异常探测可分为事物异常探测、空间异常探测、时空点事件异常探测、时空序列异常探测、时空轨迹异常探测5类。其中，时空点事件包括离群事件和热点事件：前者指存在于时空域内的孤立事件点以及少量事件的聚集；后者指显著程度较大的局部聚集[9]。Kulldorff于1997年首次提出扫描统计方法[10]并对时空热点事件进行异常探测，2001年在仅考虑空间属性的扫描模型中加入时间属性，提出时空扫描统计方法[11]，2005年进一步提出无需人口数据，仅根据区域病例数即可进行时空扫描分析的时空重排扫描统计方法[12]。该方法使用圆柱体扫描窗口对研究区域进行尺寸限定，但圆柱体扫描窗口对于不规则大型实际数据集的探测存在局限性[13]。因此，相关学者对圆柱体扫描窗口的关键参数之一——扫描形状进行了优化。例如：Duczmal等提出非圆形簇方法[14]，以提升检测非常不规则形状簇的能力；Takahashi等通过将相邻子区域组合，生成形状不规则的窗口进行扫描，提出一种灵活时空扫描统计方法[15]，并在算法中加入集群尺寸(一般为整个研究区域面积的10%～15%)控制，可进行较小尺寸异常点的检测；Kulldorff等提出椭圆形扫描窗口[16]，对潜在聚集区的形状进行限定，防止识别出过度不规则的聚集区；万幼等提出一种改进的不规则形状时空异常聚类模式挖掘方法[17]，基于时空邻近单元格构建时空邻接矩阵，对蚁群最优化扫描统计方法进行改进，使其适应时空区域扫描，有效识别了时空范围内的不规则形状异常聚类。然而，目前对圆柱体扫描窗口的另一关键参数——最大扫描半径的优化研究较少。在时空重排扫描方法中，多以50%研究区面积所对应的圆形半径作为最大扫描半径[12]，扫描半径随研究区扩大而增加，但最大扫描半径过大将导致计算资源浪费。另外，由于未有效区分和筛选实际异常点，会影响预警的准确率。为此，杨威等提出基于历史命中率的时空重排扫描方法[18]选取最大搜索半径，但该方法逐一计算不同最大扫描半径下的预警命中率，耗时较长，且仍未有效区分和筛选实际异常点，影响合适的扫描半径筛选，从而影响预警准确率。鉴于此，本文提出一种基于历史预警准确率的时空重排扫描最大扫描半径优化方法，在保证预警准确率的同时，能快速选取较小的最大扫描半径。

1 研究方法与数据

1.1 时空重排扫描方法

时空重排扫描方法的基本原理为：假设事件发生的概率在时空范围内服从泊松分布，在研究区域内划分扫描区域并将该区域内事件发生概率与扫描区域外事件发生概率之比作为扫描统计量；不断扩大扫描范围并改变位置中心，寻找出整个研究区域中扫描统计量值较大的区域。为消除扫描结果的随机性影响，对寻找出的监测点用蒙特卡洛模拟方法，筛选保留可信度较大的地点作为事件发生的预警点[12]。对研究区域以街道或其他行政区分配ID，每个ID对应一个监测点；时间节点(t=1,2,…,T)可选取天、月、年，本文以天为单位。假设研究区域某时段内某时空事件的数量和为C，其计算公式为[12]：

(1)

式中：Cot表示监测点o(o=1,2,…,O)在时间点t监测到的事件总数。

设Co表示监测点o在研究时间T内发生的事件总数，Ct表示所有监测点在时间点t发生的事件总数，则监测点o在时间点t上期望事件数量μot的计算公式为[12]：

(2)

时空重排扫描过程可模拟为一个圆柱体M的移动过程，设圆柱体M的底面圆心为扫描区域中一个监测点OM，扫描半径为RM，M的高度为研究的时间范围。每次扫描指定圆心OM，遍历所有o=1,2,…,O，o∈M，选出事件地点间距小于RM的监测点，并根据期望事件数构成期望矩阵μ=[μot],则圆柱体M内实际发生事件数量CM和期望值μM为[12]：

(3)

(4)

当CM远小于研究时间范围内发生的事件总数C时，可认为CM近似服从泊松分布，其均值为μM[19]。采用泊松模型的扫描统计量对事件聚集区进行识别和探测，通过判断事件发生数量服从泊松分布的程度，识别事件发生的独立性程度。对圆柱体M用广义似然比GLRM检验泊松分布[12，20]：

(5)

本文研究内容为热点事件聚集的监测，即只考虑CM>μM的情况。为计算方便，使用对数化处理后的形式，即对数广义似然比(LGLRM)(式(6))。LGLRM越大，说明柱体M内事件聚集性越强。通过蒙特卡洛模拟方法对聚集性较高的监测点进行显著性检验，计算在对数似然比下的概率估计P值，最后选择P值较小的监测点作为发生异常事件的预警点。

(6)

式中：u为指示函数，在CM>μM情况下，指示函数为阶跃函数，u=1。

1.2 实际异常点判定及历史预警准确率

(7)

(8)

利用该方法得到的预警结果中包含的假异常点更少，历史预警命中率较高，从而可更准确地预警出类似事件发生可能性更大的监测点。本文将历史预警准确率(α)定义为：在给定空间范围内，对历史数据通过时空重排扫描方法预警到发生异常事件的监测点数量(β1)与实际发生异常事件的监测点数量(β2)之比(式(9))，其中β1≤β2，β2>0，β1/β2∈[0,1]；将预警准确率(λ)定义为：在给定空间范围内，对研究数据通过时空重排扫描方法预警到发生事件的监测点数量(γ1)与实际发生事件的监测点数量(γ2)之比(式(10))，其中γ1≤γ2，γ2>0，γ1/γ2∈[0,1]。

α=β1/β2×100%

(9)

λ=γ1/γ2×100%

(10)

1.3 基于历史预警准确率的时空重排扫描最大扫描半径二分选取方法

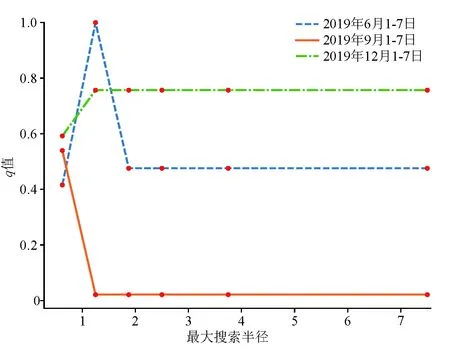
基于历史预警准确率的时空重排扫描方法最大扫描半径的优化，就是在搜索区间内寻找使得历史预警准确率最高的最小半径。本研究采用一维搜索方法寻找最佳半径。精确一维搜索常用于求解非线性函数极值点[21，22]，对函数的连续性、可微性没有严格要求，只要求选定的插入点有对应的函数值即可，因此普适性较好。精确一维搜索算法中的二分法通过取值试探的方式，求解原函数的导函数，即通过求解非线性方程的根获得最优解。假定在搜索区间[a,b]内取中点c(c=(a+b)/2)，同理在区间[a,c]、[c,b]内分别取中点d、e(d

本文以历史预警准确率为目标函数的原函数，在选定的扫描半径区间内是一个非连续性函数，不存在导函数。为得到最优半径或最优半径所在区间，借鉴二分法思想，不求解目标函数的导函数，而采用试探选点的方法,即:确定搜索起始区间后，选择一个搜索区间的中点作为试探点，计算试探点相应的函数值并进行比较，以确定新的搜索区间；不断重复该过程，将区间缩小至给定搜索区间的精度范围，若搜索区间达到设定的区间间隔精度，停止二分搜索，逼近最优值。综合不同历史时段预警结果，选择半径长度最小、历史预警命中率最高的扫描半径作为最优扫描半径。与文献[18]确定最大扫描半径的方法相比，该方法在保证历史预警准确率的前提下，试探选点比顺序选点选取的次数更少，能快速选取较小的最大扫描半径，再利用该半径进行前瞻性的区域时空重排扫描，可减少因最大扫描半径过大引起的计算资源损耗。具体步骤如图1所示。

图1 最大扫描半径二分选取流程Fig.1 Flow chart of dichotomy selection of maximum scanning radius

1.4 实验数据

相关研究[24-26]证明，火灾事件可以使用时空扫描方法进行时空异常探测。为便于实验结果的验证，本文从旧金山地区数据协调网站(https://datasf.org/opendata/)提供的“Fire Department Calls for Service”数据集中提取2018-2020年的火灾事件数据进行实验。由于公共安全事件预警通常为短期预警，因此，本文选取1周作为事件监测与预警的时间阈值，以增强事件间的相关性[27]；同时通过耗时验证方法有效性，即前瞻性时空重排扫描统计分析的运行时间。为减少实验结果的偶然性和随机性，本文设计了3组实验对结果进行验证;为验证选择不同最大扫描半径的探索效果，实验中引入q统计量作为分层异质性的探测方法[28]。通过对旧金山地区2018-2020年的火灾事件进行预处理，获取可进行时空扫描的数据。对研究的40个监测点进行编号(表1)，并筛选统计出监测点相应的火灾事故数据(表2)。

表1 监测点对应编号Table 1 Corresponding numbers of monitoring points

表2 监测点火灾事件统计Table 2 Statistics of fire incidents at monitoring points

2 实验与结果分析

采用回顾性时空重排扫描分析方法对40个监测点进行实验，选取2019年4个不同时间段(3月1-14日、6月1-14日、9月1-14日、12月1-14日)的实验数据，作为预警对比数据。为避免局部异常，基于2018年相同研究月份的数据，绘制相应监测点的火灾事件分布箱线图(图2)。

图2 2018年3月、6月、9月、12月监测点火灾事件分布Fig.2 Fire incident distribution at monitoring points in March,June,September and December 2018

2018年3月、6月、9月、12月，分别在一天内发生大于2起、1起、0起、1起火灾事件(图2中粗横线对应数值)，即异常行为。本研究分析时间为一周(d=7)，利用式(8)计算出各监测点的异常事件数阈值分别为14、7、0、7。根据阈值大小以及2019年3月8-14日、6月8-14日、9月8-14日、12月8-14日各监测点实际发生火灾的情况(图3中虚线对应刻度值为观测点研究时间段内发生异常事件数的阈值)，筛选出研究时间段内发生火灾事件的实际异常监测点(表3)。因2019年3月8-14日各监测点均无火灾事件发生，故实验中省略3月的数据。针对其余3个时间段的数据，参照本文方法，以[0 km,10 km]为二分法的搜索起始区间，以0.1 km为搜索区间的最小间隔精度(即当搜索区间的间隔小于等于100 m时停止搜索)，通过比较试探选取最大扫描半径，利用式(9)计算历史预警准确率，连续二分缩小搜索区间，得到最佳的最大扫描半径为1.25 km(表4)。

表3 2019年6月、9月、12月实际异常监测点统计Table 3 Statistics of actual abnormal monitoring points in June,September and December 2019

图3 2019年3月8-14日、6月8-14日、9月8-14日、12月8-14日实际异常监测点Fig.3 Actual abnormal monitoring points from March 8th to 14th,June 8th to 14th,September 8th to 14th,and December 8th to 14th,2019

表4 2019年6月、9月、12月基于本文方法的扫描结果历史预警准确率Table 4 Historical warning accuracy of the scanning results based on the proposed method in this paper in June,September and December 2019

地理现象普遍具有空间分异性。分异及因子探测器可以探测因变量(研究区域火灾事件发生的预警准确率)的空间分异性，探测影响因子(最大扫描半径)对因变量的空间分异性解释程度(本文用q统计量表示[28])。对本文方法在不同最大扫描半径下的空间聚集情况进行分析(图4)，可以看出，第1组实验数据(2019年6月)的q统计量在最大扫描半径为1.25 km时最大，且接近1；第2组实验数据(2019年9月)的q统计量随最大扫描半径的增大而减小，在最大扫描半径为1.25 km时，q统计量不再发生变化；第3组实验数据(2019年12月)的q统计量随最大扫描半径的增大而增加，在最大扫描半径为1.25 km时，q统计量不再发生变化。综上，在最大扫描半径为1.25 km时，空间分异性显著，影响因子对研究区域火灾事件发生的预警准确率解释度较好。

图4 3组实验数据在不同最大扫描半径下的空间异质性情况Fig.4 Spatial heterogeneity of three groups of experimental data under different maximum scanning radii

本文借助测试集(2020年1月8-14日数据)验证各方法的预测效果与泛化能力。如表5所示，本文方法与文献[12]、文献[18]方法的RMSE、MAE与MAPE相同，表明3种方法在泛化能力、预测效果方面一致，但本文方法选取的最大扫描半径最小、耗时最短，优于另外两种方法。

表5 3种方法泛化能力、预测效果及耗时比较Table 5 Comparison of generalization ability,prediction effect and time consumption of the three methods

为减少实验结果的偶然性和随机性，选取2020年1月1-7日、2月1-7日、3月1-7日3组数据进行对比实验，并将2020年1月8-14日、2月8-14日、3月8-14日的数据作为验证数据。用3种最大扫描半径进行时空重排扫描并统计扫描耗时(表6)，发现本文方法在保证预警准确率的前提下，选择1.25 km作为最大扫描半径，耗时最短，效率最高。

表6 2020年1月、2月、3月时空重排方法及其优化方法时空重排扫描结果预警准确率及耗时对比Table 6 Comparison of early warning accuracy and time consumption of the scanning results of spatiotemporal rearrangement scan statistic method and its optimization method in January,February and March 2020

3 结论与展望

时空重排扫描统计方法是时空事件异常探测的常用方法，为扩展其普适性，本文提出一种基于历史预警准确率的时空重排扫描最大扫描半径优化方法：考虑历史数据集的同期平均值对实际异常点的影响，采用二分法对历史时空数据集进行回顾性时空重排扫描统计分析；选择预警准确率最高的最大扫描半径作为前瞻性扫描统计分析的最大扫描半径。该方法在保证预警准确率的前提下，缩短了寻找合适最大扫描半径的计算时间，从而优化了时空重排扫描统计方法的性能；在半径选择过程中，虽然会占用一些计算资源，但考虑到同一观测点的长期观测研究，可为未来预警节省更多计算资源。该方法仍存在不足之处：在筛选实际异常点时，使用历史数据的同期均值作为判断阈值，扫描预警可能会遗漏发生事件数较少的部分异常点；在选择合适的最大扫描半径时，需对研究区域历史数据进行处理，对于历史事件数量较少或缺失的监测点，会降低其普适性。今后将继续对上述问题进行改进。