考虑周期性波动因素的航班离港延误时间预测*

张启凡 王永忠 王圣堂 裴柯欣

（中国民用航空飞行学院空中交通管理学院 广汉 618300）

1 引言

受到管制、天气等因素的影响，航班延误的情况时有发生。由于造成航班延误有很多潜在且不确定的因素，所以目前还未有有效的方法可以避免航班的大面积延误。因此，对于航班延误时长的预测可以为管制放行的决策提供指导。国内外学者根据航班延误中的不确定因素，建立了诸多模型［1～7］并对其进行大量的预测研究。

研究表明航班延误中天气因素大约占到65%，本文基于前人的研究，主要基于气象数据并考虑包括气候、季节、交通需求在内的周期性因素对航班延误时长的影响［8］，通过对历史数据的分析，建立考虑周期性波动因素的神经网络模型，用于未来时间内航班延误时长的预测。

2 研究数据的采集与处理

2.1 METAR的解析与转换

本文所选取的气象数据采集于航空例行天气报告（METAR），报文来源于 INPE's BDM website。依据METAR报文中各气象要素的编码格式和气象电报术语对报文进行解析。

1）利用正则表达式按各气象要素的编码格式从METAR中提取：时间、地面风向、风速、云底高、云量、修正海压、温度、露点温度、能见度信息；

2）风向为“0～“360”，将报文中显示风向多变的数据标注为“720”；能见度显示“9999”或缺失均标注为“9999”。

2.2 航班运行数据的处理

本文根据巴西国家民航局（ANAC）提供的数据选取2018年巴西圣保罗瓜鲁柳斯国际机场的离港航班数据5560条。由于本文主考周期性因素以及气象因素对单航班延误时长的影响，因此选取航司ID、航班号、航班离港日期、航班离港时间，作为数据集的描述性变量特征；选取航班出发的月份数据，对其依据四个季度进行虚拟变量的建立，将其从事件类型变量转换为定量变量；选取单航班离港延误时长作为目标变量特征。

2.3 离港数据集的构造

本文基于机场单航班离港延误数据进行预测，依据航班离港日期和时间对航班运行数据和气象数据进行融合，得到单航班延误时长的数据集。对数据中含有空缺值的数据进行删除。本文主要对延航班误特性进行分析研究，因此选取延误数据与正常运行数据组合训练数据集并剔除其他不相关数据。

3 基于RBF神经网络的航班离港延误时长预测

3.1 RBF神经网络

RBF神经网络是两层前馈网络，其隐藏层不是传统的神经网络层，隐层的功能是将输入向量的非线性可分离集转换为线性可分离集［9］。隐藏层的每一个神经元需计算输入数据到代表神经元聚类中心的距离，找到RBF作为激励函数的输入与聚类中心的距离r。第二层是一个简单的前馈层，网络输出由隐含层的输出结果经感知神经元或ADA⁃LINE线性加权输出［10］。最常用的径向基函数是高斯核函数，形式为

其中xc为核函数中心，σ为函数的宽度参数，控制了函数的径向作用范围。

xk为第k个输入样本，cj为第j个中心点，m为隐含层的结点数，n是输出的样本数［11］。可得到网络的输出为

Poggio和Girosi已经证明，RBFNN是连续函数的最佳逼近，而非BPNN。

3.2 周期性变量

为证明周期波动因素影响的存在，图1为四个季度单航班平均延误时长。可以看出四个季度的航班延误时长分布并非呈现平滑趋势，而呈明显波动趋势。所以考虑周期性变量对预测结果有重要的影响。

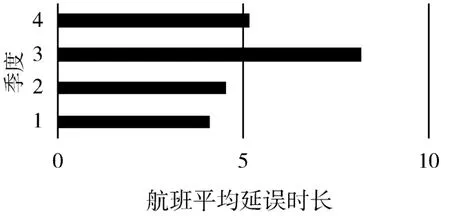
图1 航班平均延误时长周期分布

3.3 模型参数设置

考虑周期性因素的模型中RBF输入神经元节点数为数据集中的定量变量与虚拟变量个数共13个变量分别为一季度、二季度、三季度、四季度、第一层云类型、风向、风速、云底高、云量、QNH温度、露点温度、能见度，未考周期性因素的模型中则只输入定量变量即输入层神经元节点数为9；隐单元神经元节点数设置为50；选择高斯核函数作为激励函数；输出神经元节点数为1，对应变量为离港航班延误时长。

3.4 模型仿真与评价

模型经运行后得到仿真结果如图2～3所示，图2为未考虑周期性波动因素的仿真结果，图3为考虑周期性因素后的仿真结果。

图2 RBFNN仿真结果

图3 RBFNN考虑周期性因素仿真结果

为验证模型延误时长预测的准确度，用延误时长容差准确性来评价模型的准确度得到结果如表1所示。

表1 RBFNN仿真结果评价

改进后的模型在三个容差范围内均有较高的准确性，说明航班的延误时长是会受到包括气候、季节、交通需求等因素在内的周期性波动影响。

4 对比模型仿真实验

4.1 BP神经网络与小波神经网络

本文在研究过程中同时还采用了BP神经网络和小波神经网络进行了仿真实验，用以进行模型准确度的对比和最优模型的验证。

小波神经网络的结果基于小波理论，其因隐藏层激励函数采用小波函数，所以其学习能力和精确度较高，选用Morlet作为激励函数，若输入层、隐含层、输出层节点数为h、k、n，输入和输出集分别为x=［x1，x2，…，xk］T、y（x）=［y1，y2，…，ym］T，得到小波神经网络的隐单元表达式为

式中，aj、bj分别表示小波神经网络的伸缩和平移参数，wi，j、wj，h分别表示输入单元到隐单元的权重值、隐单元到输出的权重值。

小波神经网络输出层表达式为

4.2 模型参数设置

BP神经网络在预测时为三层网络，其中输入层节点个数为自变量个数，隐单元节点数为60，隐含层函数tansig［12］，输出层函数 purelin［13］，学习率设置为0.001，gaol为0.0001，最大迭代次数1000次。小波神经网络在预测时隐单元节点数为30，隐单元为Morlet核函数，学习率［14］设置为0.001，最大迭代次数1000。

4.3 模型仿真与评价

模型经运行后得到仿真结果如图4～5所示，图4为BPNN未考虑周期性波动因素的仿真结果，图5为考虑周期性因素后的仿真结果。

图4 BPNN仿真结果

图5 BPNN考虑周期性因素仿真结果

图6为WNN未考虑周期性波动因素的仿真结果，图7为考虑周期性因素后的仿真结果。

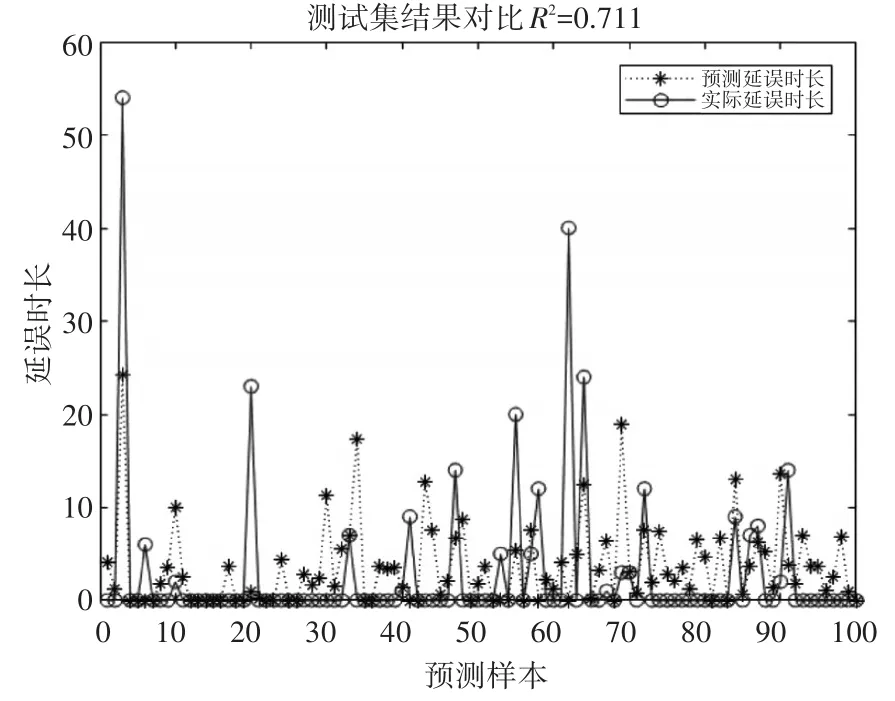
图6 WNN仿真结果

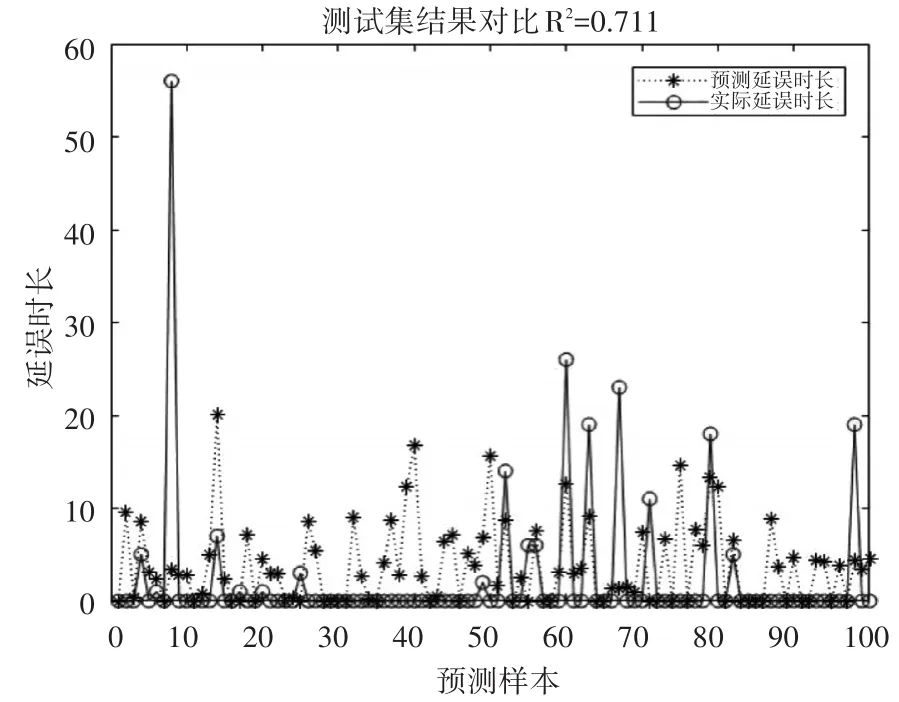
图7 WNN考虑周期性因素仿真结果

同样，用延误时长容差准确性来评价模型的准确度得到结果如表2所示。

表2 BPNN及WNN仿真结果评价

从上表可以看出小波神经网络的精确度高于BP神经网络，且采用考虑周期因素后的模型的准确度均有提升。RBF神经网络的预测精确度最高，同时本文还将改进后RBF的神经网络模型的仿真结果与文献［7］中弹性神经网络的仿真结果进行了对比，本文模型在容差（±3min）内的准确率为91%高于文献［7］仿真结果83.954%。

5 结语

本文通过绘制延误时长周期分布图，发现延误时长并非呈平滑趋势而会受到包括交通需求、气候、季节在内的周期性因素波动的影响。利用RBF神经网络建立仿真模型，输入经筛选后的定量变量与周期虚拟变量共13个。运行得到仿真结果，±10min、±5min、±3min容差内延误时长预测准确率分别为98%、94%、91%，相较于未考虑周期性波动因素模型表现出较高的准确性。小波神经网络和BP神经网络在考虑周期性波动因素后准确度也得到提升，但模型预测准确度远不及RBF神经网络。此外，因数据样本的关系，本文未过多考虑管制因素的影响，后续的研究中可以进一步地挖掘相关因素从而再次提升模型预测的准确度。