道路抢险工程机械机群配置建模方法*

杜毛强 何晓晖

（1.陆军工程大学野战工程学院 南京 210007）（2.中国人民解放军32228部队 厦门 361100）

1 引言

自然灾害的发生往往导致道路损坏、交通阻塞，工程机械成为道路抢险不可或缺的装备。在应对自然灾害对道路造成的多处破坏时，通常由多台不同种类的工程机械组成的机群来完成抢险任务，而如何配置机群使得任务在最短时间内完成亟待解决的问题。现有对抢险施工资源配置建模的研究大都以价值系数法［1～2］评价机械施工效率，缺乏对施工过程及机械作业工序的考虑。

利用Petri网模拟土方施工过程逐渐引起了研究者的兴趣［3～5］。Petri网是离散事件动态系统建模和分析的主要方法之一。近年来，Petri网已广泛应用于设计制造、网络系统、工程施工等离散事件系统的仿真。而在道路抢险施工中，由于空间限制导致工作面有限，在多台机械同时施工的情况下机械往往需要排队作业。增加机械数量可以加快抢险进程，但又会因为排队造成机械效率低下，浪费了资源。因此，建立抢险工程机械机群配置模型显得尤为重要。根据已有的相关研究，排队论是解决上述问题的有效方法。本文在分析道路抢险施工过程的基础上，建立了抢险施工排队网络的着色Petri网（colored Petri net）模型，得到抢险施工的时间计算表达式，进而提出抢险工程机械机群的配置模型。

2 道路抢险施工方法

道路损阻的主要类型有：1）土石阻塞，如山体滑坡、崩塌、泥石流等造成的土石堆积，阻塞道路；2）路面损毁，如路面下限、张拉开裂、变形错位等；3）路基损毁，如路基沉陷、路基坍塌等。抢险施工的目的就是在最短时间内恢复并保障通行。常用的道路抢险工程机械有推土机、挖掘机、装载机等，各机械协同配合进行挖、装、运、推等工作，在一定工序下完成抢险任务［6］。应对各类型的抢险任务的工程机械种类和主要作用如表1所示。

表1 道路抢险工程机械的作用

3 道路抢险施工排队网络着色Petri网模型

3.1 抢险施工排队原理

当多台同类机械进行同一作业时，我们可以将待施工的土石方看作服务台，施工机械看作等待服务的顾客，机械施工看作接受服务。假设施工机械的到达率符合泊松分布，机械和作业面就构成一个M/M/1/m型排队系统，即服务台数量为1，顾客源为限额m，到达时间间隔相互独立并符合负指数分布，服务台服务时间间隔符合负指数分布［7］。其排队原理见图1。

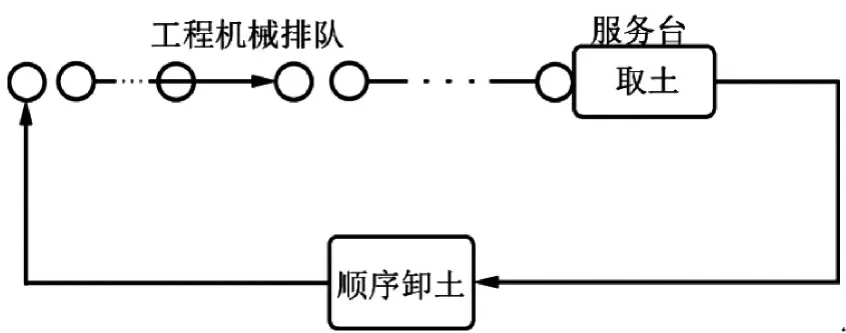
图1 工程机械施工排队原理

系统主要指标为

顾客平均到达率λ，平均到达时间间隔1/λ，平均服务率μ，平均服务时间1/μ，服务台空闲概率［8］：

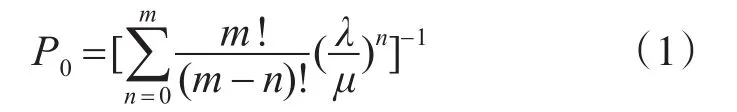
由此可以得到m台斗容量为V的工程机械完成土方量为Q的时间为

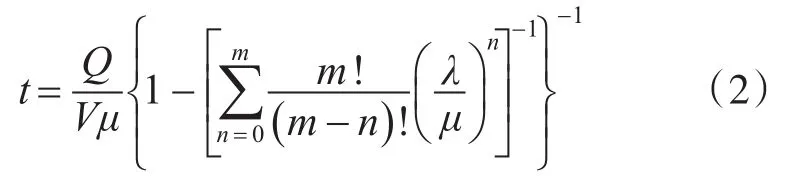
路基损毁抢险施工时，首先由挖掘机挖除损坏路基，同时挖掘机就近取土，待损坏路基挖除后，由装载机运送土方至损毁处回填，与推土机配合分层压实土方。装载机装卸土方和推土机分层压实构成了一个二级循环排队系统［9］，如图2所示。

图2 二级循环排队系统原理

由于推土机每完成一次装土后装载机才可以卸土，服务台II的平均服务时间即推土机装土作业的时间1/μT。由于推土机推土与装载机装载时间不同，即μT≠μZ。用Z表示装载机数量，服务台I空闲的概率［10］可表示为

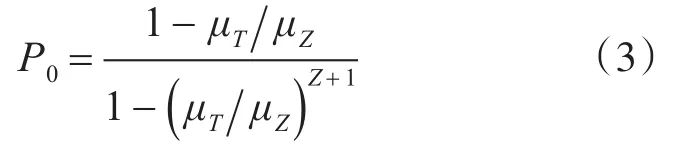
施工时间为

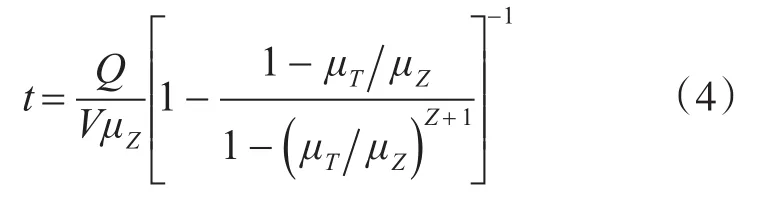
3.2 着色Petri网基本定义

道路抢险施工过程是动态的离散过程，工序之间的搭接关系可以用Petri网中变迁之间的流关系表示［11］。一个着色Petri网系统是定义为一个9元组：CPN=(P，T，F，Σ，V，C，G，E，I)。其中：

1）P是n维库所的有限集。

2）T是m维变迁的有限集，且P∩T=∅。

3）F是弧的有限集，称为流关系，记作F⊆P×T∪T×P。

4）Σ是一个有限非空的颜色集集合。

5）V是一个有限的类型变量集合，所有的变量满足v∈V。

6）C是一个颜色集函数，为每一个库所分配一个颜色集。

7）G是一个警卫函数，将变迁映射为布尔函数。

8）E是一个弧表达函数，将F映射为其相邻库所颜色的多重集和延迟时间，这个延迟时间代表活动的持续时间。

9）I是一个初始化函数，为每个库所分配一个初始化表达式［12］。

库所集和变迁集是有向网的基本成分，流关系是从它们构造出来的。每个库所代表一种资源，资源的流动由流关系规定。将抢险机械作为库所的元素，机械和土石方的状态变化过程作为变迁来建立Petri网仿真模型，可以描述抢险施工系统的动态变化情况。

3.3 CPN模型

本文采用CPN Tools软件工具建立和分析Petri网模型。CPN Tools是用来模拟和分析着色Petri网的编辑仿真软件，可利用其建立排队系统的层次网（Hierarchical Nets）。该软件提供监视器（Mon⁃itor）功能，可以在仿真过程中记录动态数据［13］。

3.3.1 单服务台排队系统

土石阻塞路面时，通常配置1台挖掘机配合装载机装卸转运土石。装载机卸土时不存在排队现象。当装卸和平整的土石方量达到任务量时，可视为仿真结束。此处以土石阻塞抢险施工装载机排队装卸过程为例，利用CPN Tools建立CPN模型，如图3所示。

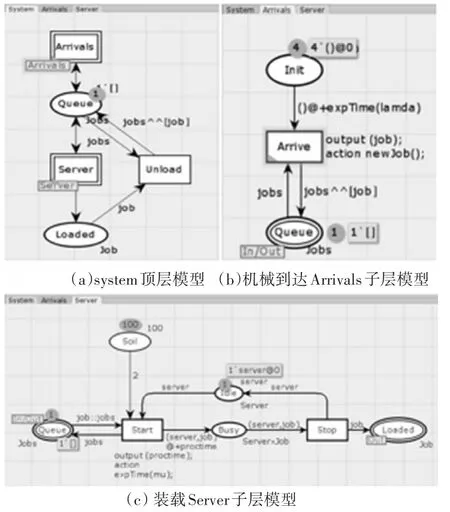
图3 装载机排队装卸过程CPN模型

图3依次描述了装载机装卸排队过程的总体结构、装载机到达过程以及作业排队过程，模拟了单服务台排队系统。机械（记为job）通过替代变迁Arrivals产生并加入到队列（库所Queue）中，到达时间间隔服从负指数分布（expTime函数）。服务台通过替代变迁Server对job进行服务，即装载机到达后开始装载，作业时间间隔服从负指数分布（exp⁃Time函数）。满载完成后将job送入库所Loaded，然后进入变迁Unload开始卸土，最后加入队列Queue完成一次循环。相关的变量和颜色集声明如图4所示，其中lamda，mu分别表示平均到达时间间隔和平均服务时间。

图4 变量和颜色集声明

3.3.2 二级循环排队系统

图5描述了由装载机和推土机机群构成的二级循环排队系统。装载机到达时间间隔服从负指数分布（expTime函数），作业时间间隔服从负指数分布。装载完成后进入库所Queue2，开始卸土（回填）排队。推土机服务台II的平均服务时间为推土机装土时间，服从负指数分布。装载机完成卸土后进入库所Queue1，回到装载队列。

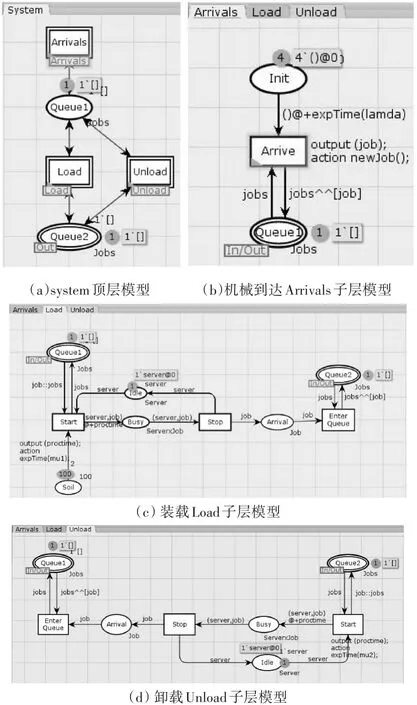
图5 二级循环排队系统CPN模型

3.4 仿真结果及分析

假设装载机平均到达时间间隔为10，平均装载时间为10，推土机平均装土时间为5，待装载的土方量为100，单次装载土方量为2，对单服务台系统模型进行仿真。通过监视器功能Data Collection得到仿真结果如图6所示。

图6 仿真结果

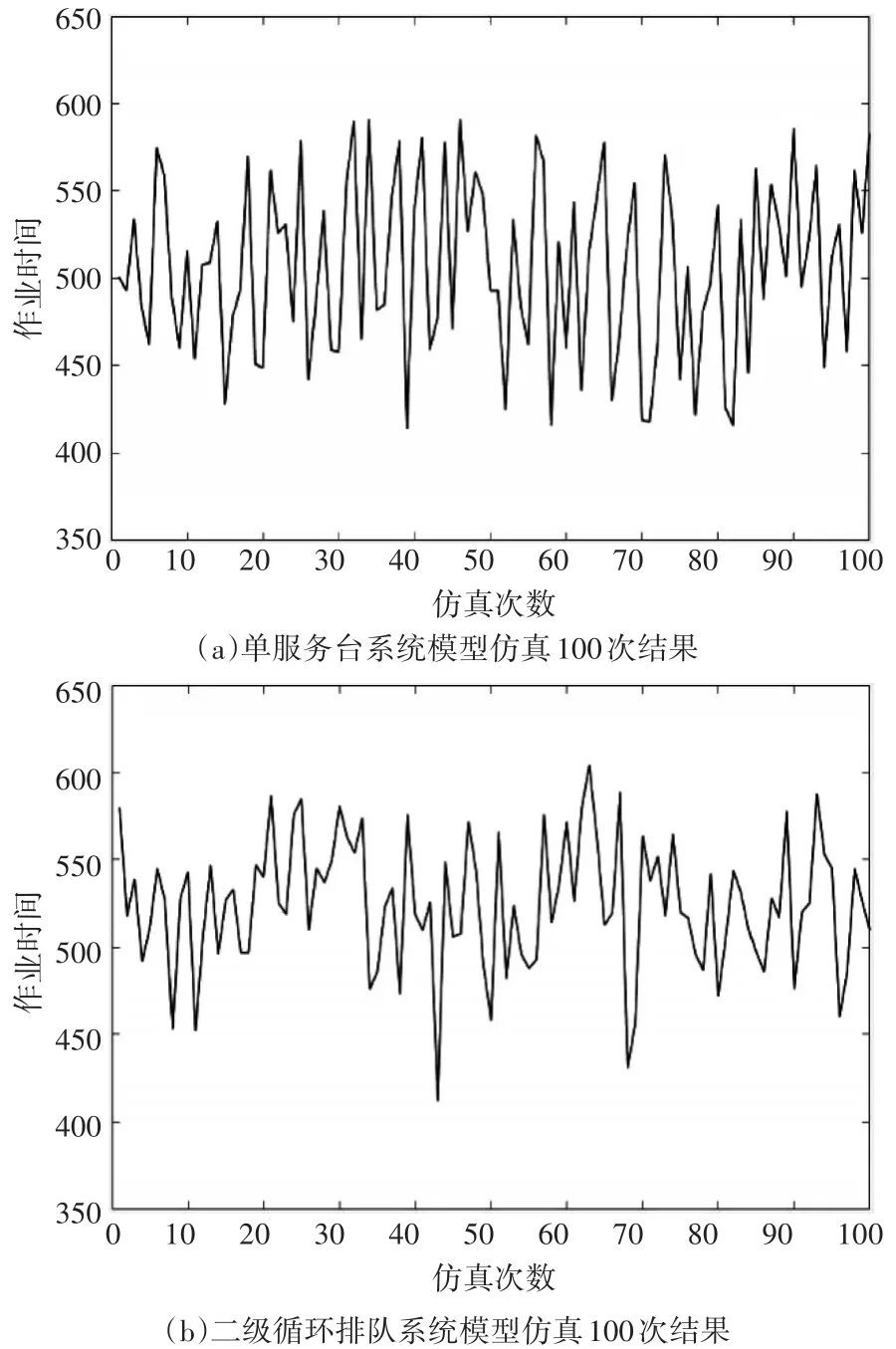
图7 CPN模型仿真100次结果

可以看出，模型分别运行了154步和304步得到的仿真时间为493、580。对模型分别仿真100次，其结果如图5所示。仿真结果和理论值对比如表2所示。

表2 仿真值与计算值对比

可以看出，仿真作业时间与理论作业时间非常接近，应用着色Petri网可以对排队系统建模、仿真，利用排队论计算工程机械抢险施工的时间是有效的。

4 机群配置模型

4.1 问题提出

某地突发自然灾害，导致土石阻塞、路面损毁、路基损毁各一处，估算土石方工程量分别为Q1，Q2，Q3。现有推土机、挖掘机、装载机等三类抢险施工机械组成的机群，数量各T，W，Z台，单次作业土方量分别为VT，VW，VZ，作业循环时间分别为1/λT，1/λW，1/λZ，单次取土耗时分别为1/μT，1/μW，1/μZ。各任务的机群配置方案可表示为

考虑每个情况如何配置机群，能够使抢险施工总任务完成的时间最少。由于总任务完成的时间等于各任务完成时间ti的最大值。抢险施工工程机械机群配置模型的目标函数为

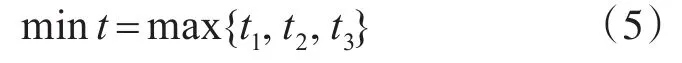
4.2 抢险施工时间计算方法

已知同类机械到达排队系统时间间隔服从负指数分布，机械作业装置满载一次的时间服从负指数分布。根据排队论原理和Petri施工模型，完成土石方量为Q1的土石阻塞抢险施工时间为

同理，路面损毁抢险可看作三个串联的排队系统，其任务施工时间为

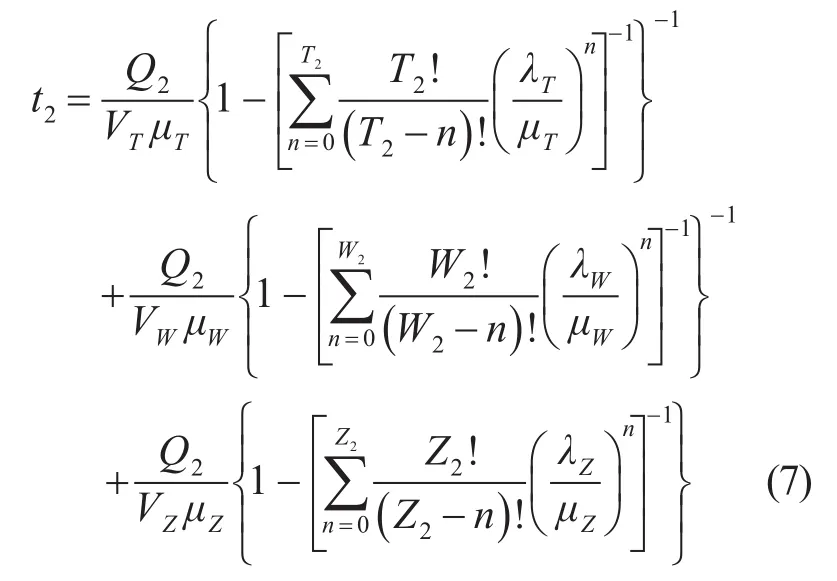
路基损毁抢险施工时，装载机和推土机机群构成一个二级循环排队系统。其抢险施工时间为

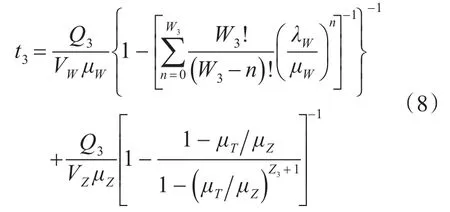
4.3 机群配置的数学模型

抢险施工机械机群配置的目的是求解最优配置方案X，约束条件为各类机械配置数量之和不超过现有数量。通过对问题的分析，可建立如下数学模型：

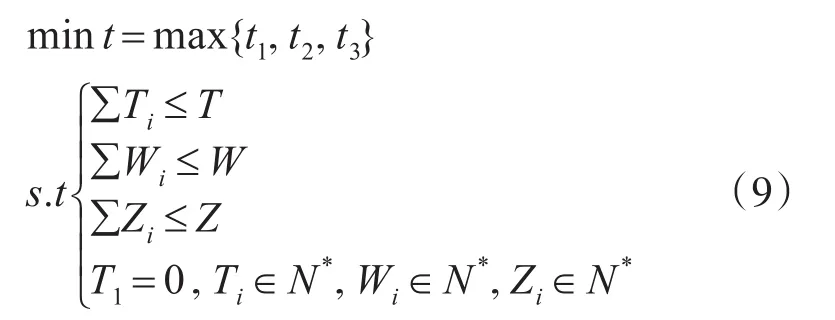
5 结语

1）分析了工程机械担负道路抢险施工的任务特点和方法流程，提出利用排队论计算道路抢险施工时间。

2）建立了工程机械机群施工排队的网络的着色Petri网模型，利用软件CPN Tools进行仿真，验证了机械施工时间计算方法的有效性。

3）提出了道路抢险工程机械机群配置的数学模型。该模型旨在解决承担多任务的道路抢险工程机械机群编配问题，为求解机群的配置方案提供依据。