基于双偶极子模型的水下航行体尾迹内波仿真方法*

李万鹏 李智生

（中国人民解放军91550部队 大连 116023）

1 引言

在明显密度分层的流体环境场中，具有一定水平速度的航行体在其内运动时，会在该航行体尾部激发内波并产生相应的尾迹流场［1～2］。对航行体运动产生的内波、尾流等水动力特征的研究是实现非声学探测的基础，只有知道航行体运动产生的内波、尾流的物理特征，才能为非声学传感器的设计、参数选择及信息处理提供重要依据［3］。为获取接近真实环境条件下航行体运动激发内波及尾迹的波形结构特征，仿真的方法是最经济、最有效的技术途径，所以，水下航行体内波及尾迹仿真研究具有重要的理论价值和实际意义。

国内外研究表明，具有自航螺旋桨装置的航行体运动过程中激发内波包括体积效应、尾部湍流效应和螺旋桨效应［4～5］。Milder［6］、尤云祥［7］等研究得出等效移动质量源模型可有效模拟有限深密度分层流体中运动物体生成内波的体积效应和旋涡、湍流尾迹激发源。李广年［8］采用PIV试验技术定量分析了螺旋桨尾流速度分布。陈志明［9］、苏玉民［10］等采用不同的数值方法分析了螺旋桨尾流场结构。以上航行体相关内波研究多侧重体积效应内波，对体积效应和螺旋桨效应共同作用的尾迹内波方法研究较少。

本文针对航行体螺旋桨效应激发尾迹内波，从等效质量源模型角度出发，建立双偶极子模型，耦合航行体体积正对称效应和尾部螺旋桨尾迹反对称效应，得到接近真实环境下航行体运动激发尾迹内波的波形结构图，在此基础上，建立航行体激发内波及其运动尾迹相对应的理论和数值模型，得到更加接近真实环境条件下的航行体尾迹内波特征。

2 双偶极子模型控制方程

2.1 基本控制方程

本文统一坐标系为笛卡儿坐标系，同时假设分层流体无粘、不可压缩、绝热，且在水平向无边界限制、在垂向为有限深度。航行体模型特征长度与其激发内波的特征长度接近，在真实海洋环境下，水下自主航行体运动激发内波及其尾迹场的流场直径范围为10kg～100kg。计算过程中，我们忽略由于地球运动产生的旋转作用和地球水平面的曲率对数值模型的影响。三维空间坐标系中，oxy平面位于分层流体未扰动静止水平面，z轴正向沿铅直方向向下。对于字母标示符号，作如下设定：若符号上方有“⇀”符号，则其表示向量符号；若符号右上方有“'”则其表示对该符号进行一阶求导。

首先建立移动等效质量源，根据内波运动基本方程、不可压缩流体特性及质量守恒定律，得到密度分层、不可压缩流体的闭合控制方程组［7］：

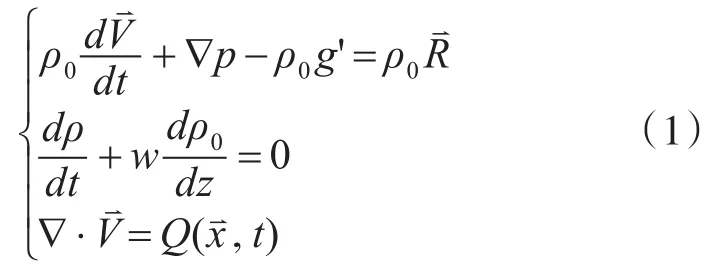
其中，g'=ρ'/ρ0g为约化重力，即单位质量流体微团在偏离平衡位置处受到浮力与重力之和。

无螺旋桨作用的运动航行体为一个沿x轴对称分布的细长体，当其沿x轴正向运动时，激发的流场可假定为关于x轴对称分布［11］。对于双偶极子，第一个偶极子可看作体积效应和尾部湍流作用的激发源，关于x轴呈正对称分布；第二个偶极子可看作螺旋桨作用激发的流场，作为一个固定直径的球体，其激发的内波尾迹流场关于x轴呈反对称分布。

2.2 基于等效质量源的双偶极子模型

等效质量源激发内波对应的色散关系式为ω=ω(k)，该式为k的单调增函数，可通过求解本征值问题式来确定［12］。

在对回转细长航行体模型生成内波进行数值模拟前，需确定等效质量源的运动速度及体积问题。对于等效质量源的运动速度，首先需要通过真实环境的实验研究，以确定模型激发内波时激发源的转捩速度，对模型的速度选取方法为转捩前的运动速度取为模型自身的运动速度；转捩后的运动速度取为激发内波的速度。对于等效质量源的体积问题，根据等效质量源的几何参数计算方法确定。

回转细长体激发内波的垂直位移场的表达式为

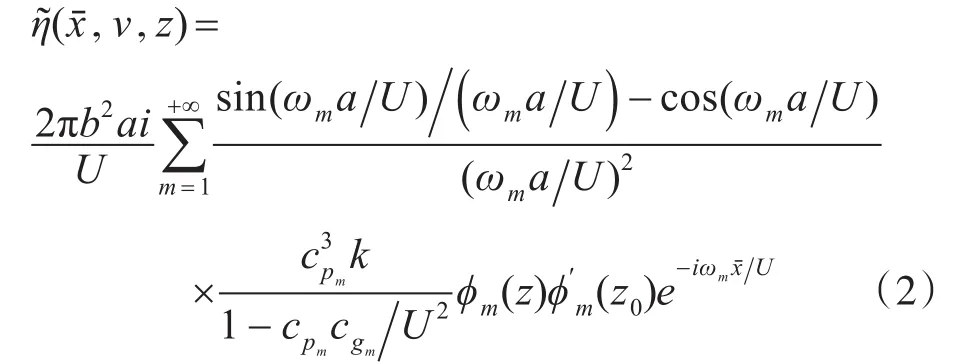
上式为单个偶极子垂向位移场表达式，根据数值分析需要，取y坐标范围-0.6≤y≤0.6，取时间范围0≤t≤150。同时，由于最终得到的数值结果图中，要求第一个偶极子模拟体积效应，其关于x轴是正对称的；第二个偶极子模拟螺旋桨效应，其关于x轴是反对称的。两个偶极子之间具有时间差Δt=t1-t2，其中t1、t2分别为体积效应时间和螺旋桨效应时间。因此，可分别得出两个等效质量源的垂向位移场表达式。

正对称等效质量源的垂向位移场：

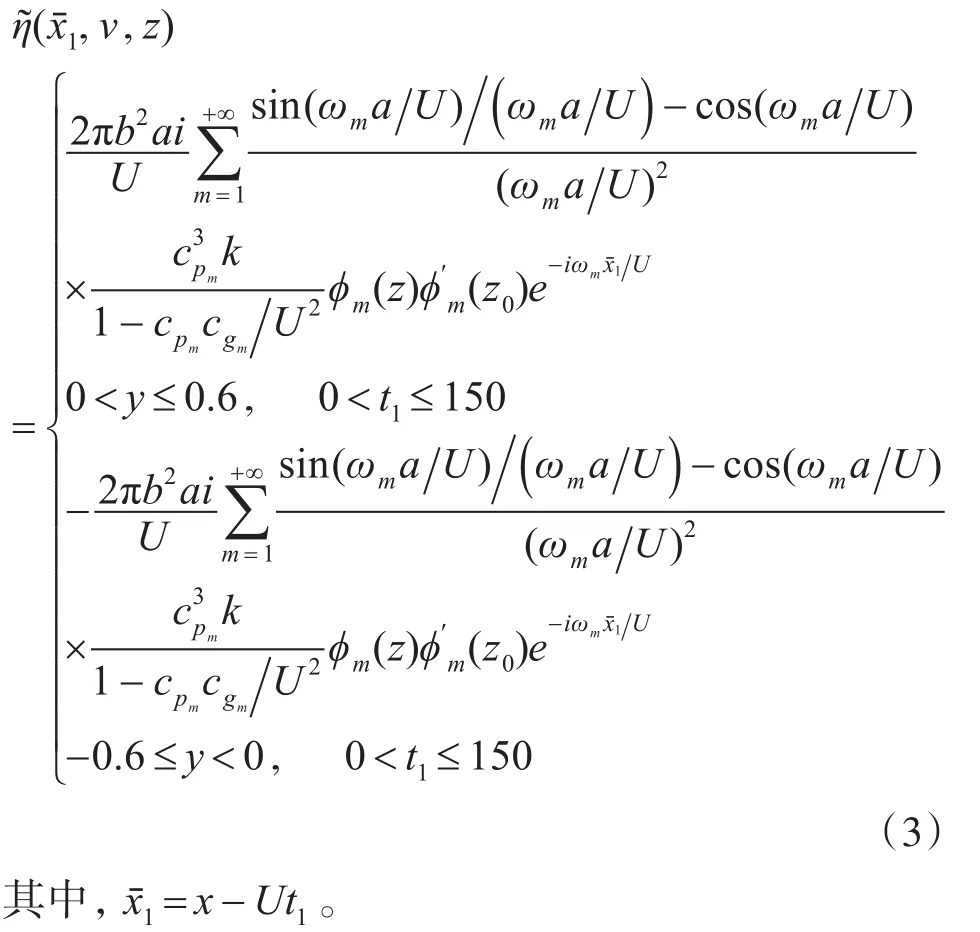
反对称等效质量源的垂向位移场：

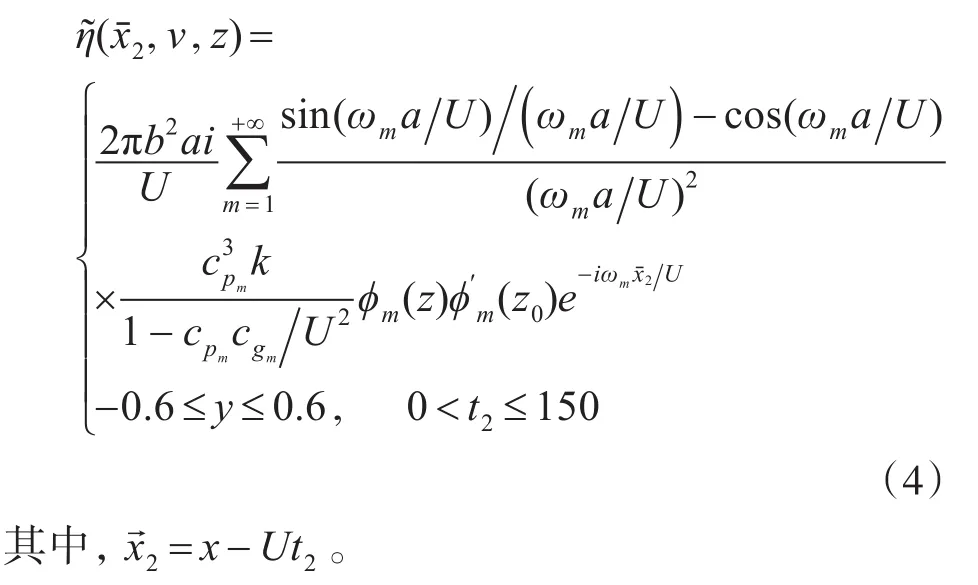
将两个等效质量源垂向位移场等效叠加处理，得出双偶极子垂向位移场表达式：

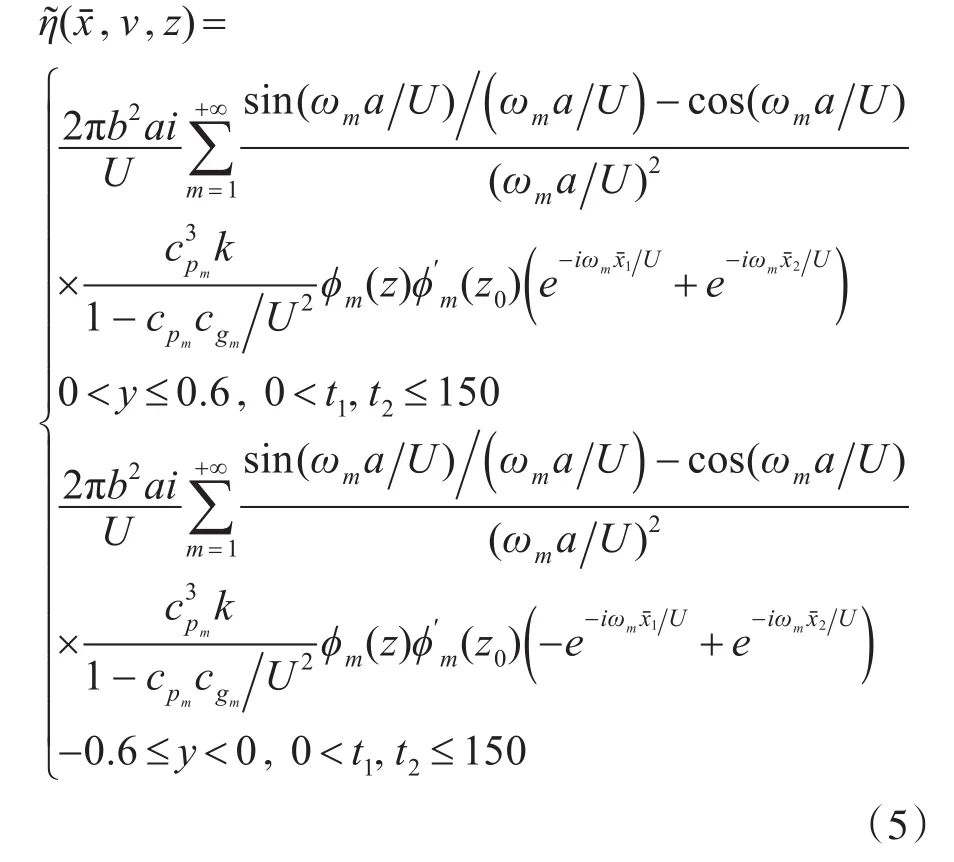
3 仿真计算及结果分析

通过对数值仿真计算结果分析，并与水池环境真实实验结果对比分析，以验证数值模型的正确性和数值模拟的真实性。

设计数值流场环境（背景流场）为浅跃层两层分层环境，上层流体垂向厚度约15cm，下层约65cm，两者交界处存在约7cm厚度的密度跃层，内波波形结构计算深度为14cm。如图1所示，在模型中设置上述参数及浮力频率垂直剖面数据等信息，得到流场密度ρ及浮力频率N垂向分布图。

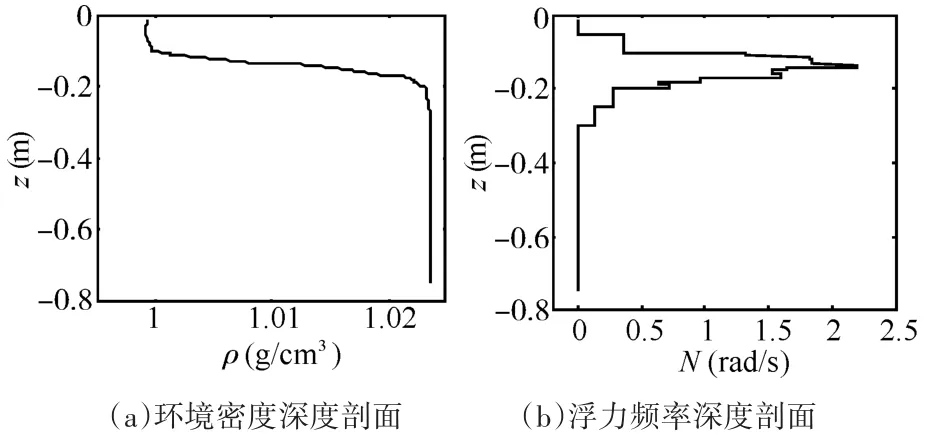
图1 环境密度及浮力频率垂向分布图

设置模型中航行体直径为7cm，长度为58cm，航行体放置深度为29cm，此时航行体运动激发内波转捩速度为58cm/s。分别选取转捩前后两个速度35cm/s和73cm/s，分别代表航行体转捩前后的波动结构图进行对比分析。

图2、图3分别为速度35cm/s、73cm/s时数值仿真内波波形结构图和水池实验波形结构图。对比分析，数值模拟得到的转捩前和转捩后内波波动结构图中波动条纹较清晰和规则，两速度下均能明显看出第一模态波动结构和第二模态波动现象，第二模态横波明显，且仿真和实验得出的波动条纹均具有明显的非对称性；第一模态波动明显，其他模态波动存在叠加现象，且不明显；第一模态存在明显的侧波，横波不可见，仿真结果波形角略大于实际波形角；第二模态横波叠加在t＞60s时，图中可明显看出叠加现象；仿真结果图中t=20s时开始出现非对称现象，而实验结果自t-15s起才出现非对称现象，该现象由模型尾部螺旋桨效应引起；对比t≥40s后的图像，波动较弱，且没有明显的湍流波动结构，原因是未在数值模型中添加湍流作用参数模型，后续需进一步改进。转捩前后分析，内波波动角度随速度的增大逐渐增加。

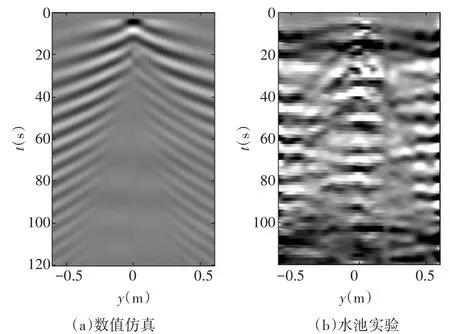
图2 速度35cm/s时数值仿真和水池实验波形结构图

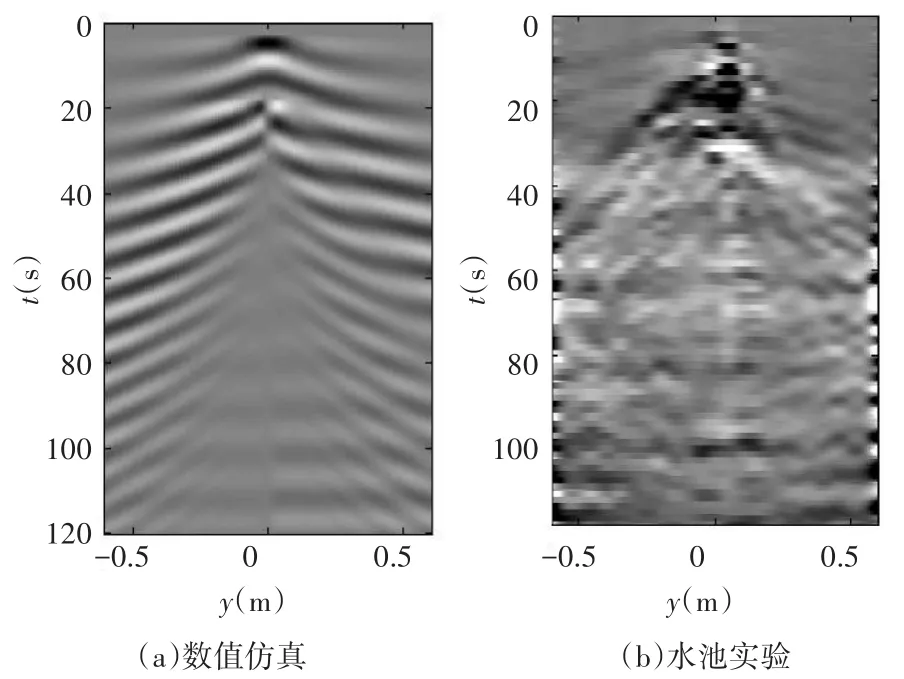
图3 速度73cm/s时数值仿真和水池实验波形结构图

图4、图5展示了转捩前后代表速度激发内波波形结构灰度时间序列图，对比分析，在t＜100s时间范围内仿真实验结果与相同工况下水池实验结果数据波动及灰度幅值变化规律基本一致，验证了该模型的可行性。从图4和图5可以看出，随着时间的推移，仿真实验结果数据趋于平滑，因仿真模型未细化考虑水槽壁面作用、湍流作用、偶极子滞后时间等复杂因素带来的真实环境参数，而水池实验结果综合了各种影响因素。

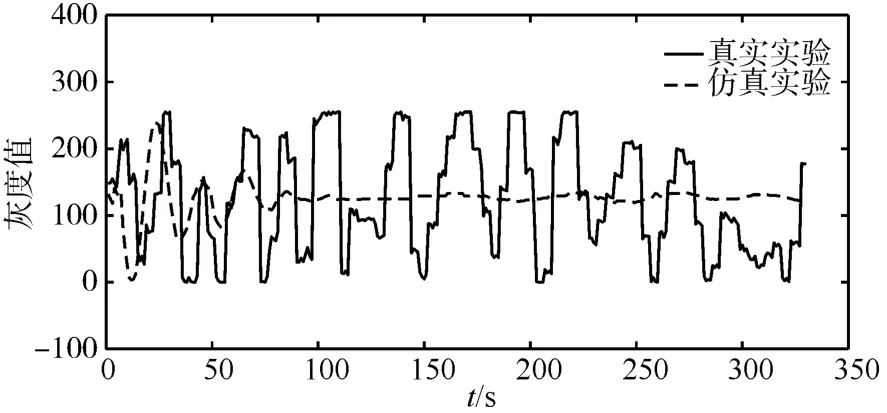
图4 速度35cm/s时水池实验与仿真实验灰度时间序列图

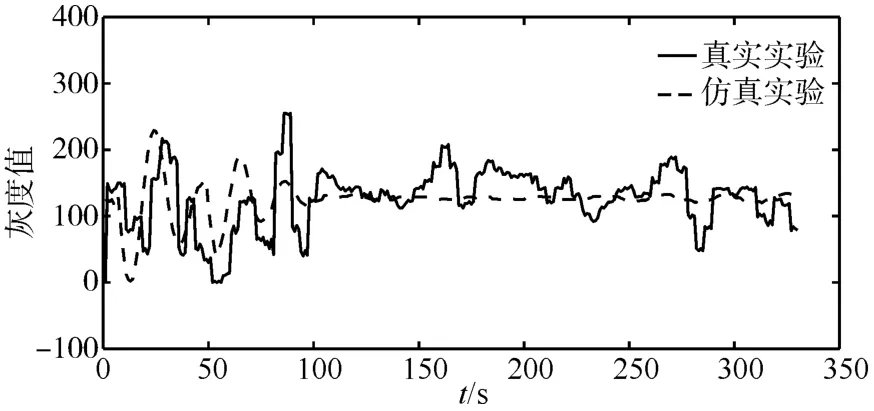
图5 速度73cm/s时水池实验与仿真实验灰度时间序列图

4 结语

本文从等效质量源模型角度，在单偶极子模型基础上，建立双偶极子模型，模拟水下航行体体积正对称效应和尾部螺旋桨尾迹反对称效应，从理论上进行耦合处理，得到接近真实航行体运动激发内波及尾迹的波形结构图。

通过建立相同工况条件，得出数值仿真实验结果，并与真实实验结果对比分析，该模型可计算出波动的不同模态随速度的变化规律、模态叠加得到的不同波动结构以及明显的非对称结构，且非对称结构开始出现时间及内波波动变化规律与真实环境水池实验结果基本一致。因此，该双偶极子模型可用于模拟真实螺旋桨效应，以便更深入地对螺旋桨效应及其相应的水动力学现象进行研究。