基于图像特征的雷达脉内调制类型识别*

高君丰 刘芬芬

（1.中国人民解放军92785部队 秦皇岛 066200）（2.中国人民解放军91404部队 秦皇岛 066000）

1 引言

由于军事技术的不断进步和发展，新体制及复杂体制雷达不断被投入使用，人们接收到的辐射源信号脉内调制形式复杂、参数多变，给识别带来了极大的挑战。针对复杂体制雷达信号的脉内调制类型识别已经成为电子对抗领域中亟待解决的关键问题。传统的识别方法包括时域自相关法［1］、相位差分法［2～4］、小波变换［5～6］等，但是这些算法抗噪性能较差，随着信噪比的降低，识别性能会急剧下降。由于不同信号之间的时频分布图差异性很大，从时频图上可以很容易地判别出信号的调制类型，所以对雷达辐射源信号进行时频变换，提取时频特征对信号分类识别是近年来的研究热点［7～8］。

本文利用图像处理方法对信号时频图进行预处理，包括图像滤波、图像剪切、图像二值化等，去掉背景噪声等冗余信息，截取出图像中信号所在部分；然后提取出图像的中心矩和伪Zernike矩特征，再利用随机森林构建分类器，识别信号的调制样式。

2 时频变换

时频分析作为分析和处理非平稳信号的有力工具，反映了信号能量随时间和频率的分布，可以在时频域上更精确地描述信号［9～10］。最常用的时频分布是魏格纳－维尔分布（Wigner-Ville，WVD），具有很高的时频聚集性，但多分量信号的WVD变换存在严重的交叉项，造成一些虚假信息的干扰，从而给信号的时频分析带来困难。学者们提出了多种抑制WVD交叉项的方法，有平滑Wigner-Ville分布（SWVD），伪Wigner-Ville分布（PWVD），平滑伪Wigner-Ville分布（SPWVD）。本文所用的SP⁃WVD采用同时对信号在时域和频域加窗平滑的方法来抑制交叉项。信号x（t）的SPWVD分布定义为

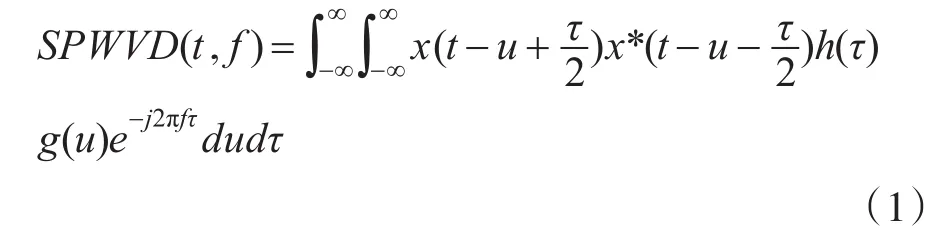
式中g（u）和h（τ）分别是时域和频域的平滑窗函数。

本文对信号的时频变换图进行了归一化操作，并将信号能量换算为以dB为单位。即时频图的y轴大小为

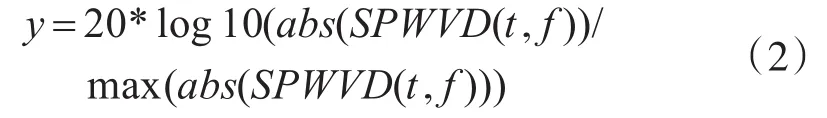
图1给出了信噪比为10dB时几种常见脉内信号的时频图，从图中可以看出，不同信号的时频变换图差异明显，肉眼很容易区分，但要实现自动识别还要结合数字图像处理技术进一步提取信号的时频特征。

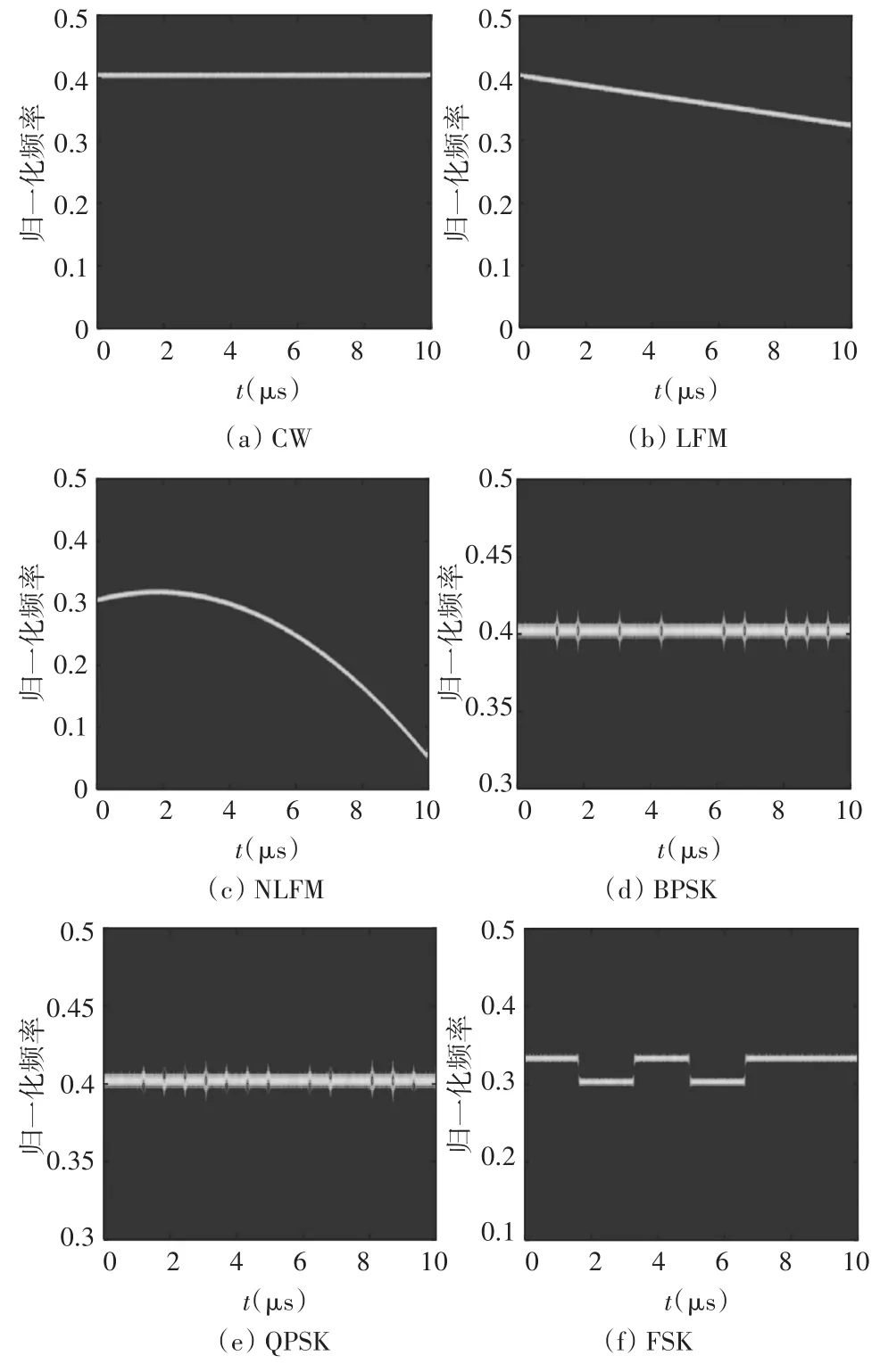
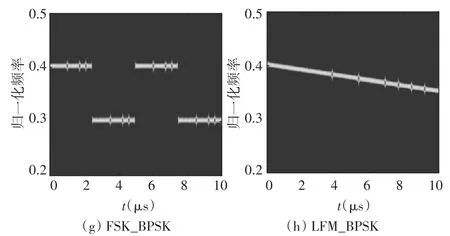
图1 8类图像的SPWVD时频图

3 图像预处理

由于时频图像受噪声影响较大，并且存在大量的冗余信息，所以在提取特征之前，需要将时频图像进行预处理，以提升图像的质量，保证所提取信号特征的有效性。

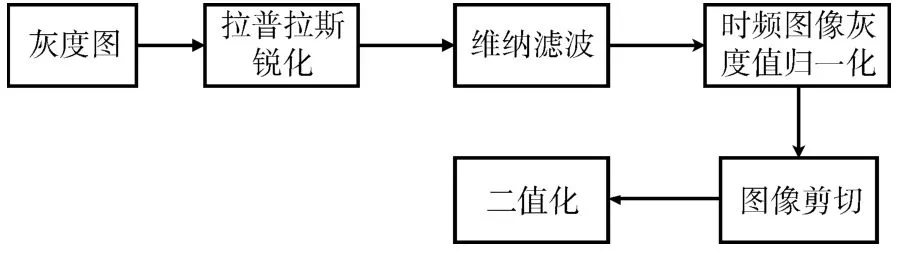
图2 图像预处理过程

首先将彩色的时频图转换为灰度图，通过拉普拉斯锐化［11］，增强图像的边缘和灰度跳变的细节部分，提高图像的对比度，从而使图像更加清晰。通过自适应维纳滤波抑制目标信号和背景中的噪声，达到图像增强的效果［12］。为了减少数据间的不均衡性，对时频图像灰度值进行归一化处理，归一化后像素点的灰度值为x=(x-)/σ，和σ2分别为所有像素点灰度值的均值和方差。从图1中可以看出，时频图中大多都是背景，并不是所有的频率点都存在信号，沿频率轴检测出信号时频分布的起止频率，将没有信号分布的图像区域剪切掉，能够减小冗余信息，有利于下一步信号特征的提取。

经过上述一系列图像预处理后，通过灰度阈值化处理将时频图像转化为二值图像，二值化使图像变得简单，且数据量大为减少，能凸显出目标的轮廓。图像的二值化处理可以描述为

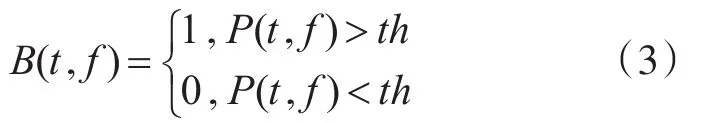
式中，P(t，f)表示信号的时频图，二值化过程中阈值th的选取采用一维最大熵法［13］。

经过预处理后的时频图像形状特征更加明显，如图3所示。

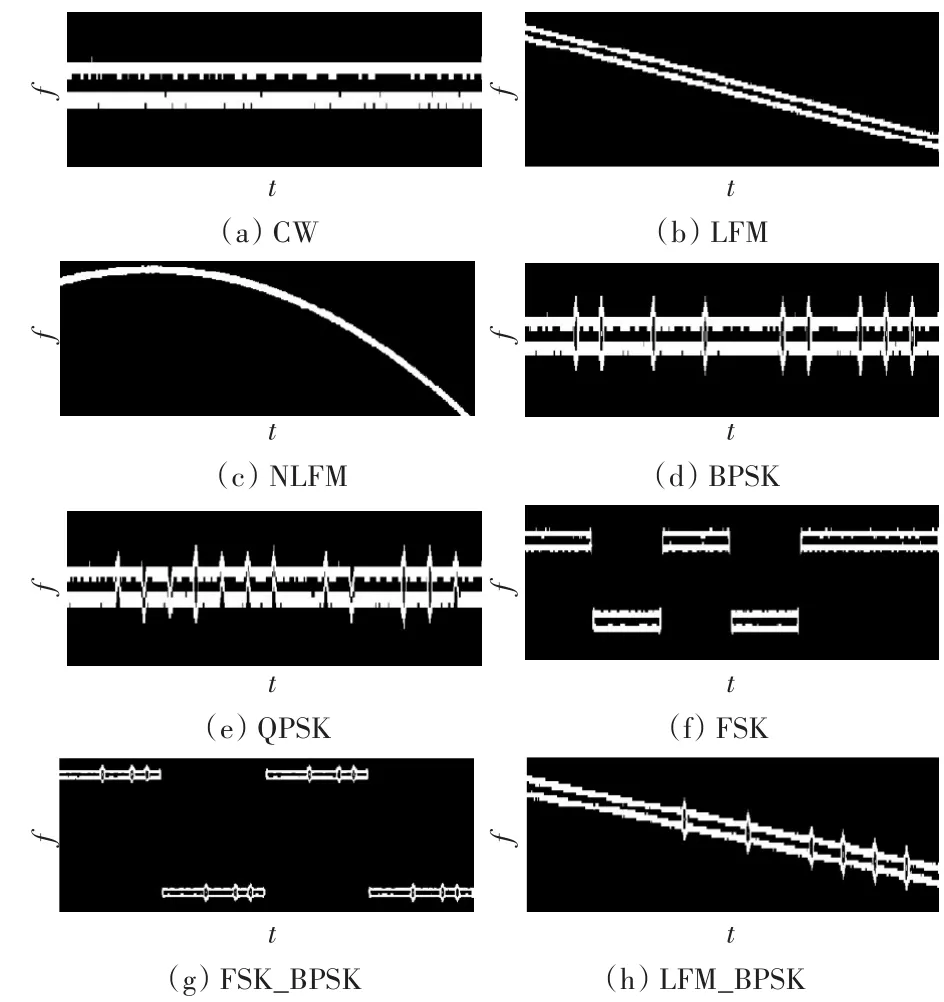
图3 预处理后的时频图

4 特征提取

由图1和图3的时频图像可以看出，不同调制类型信号的几何形状具有比较明显的差异，因此可以提取时频图像的形状特征用于信号的分类识别。矩函数是一种有效的形状特征描述子，能够提供大量与图像有关的信息，如图像的形状、大小和方向等，本文主要选取了矩函数中的归一化中心矩以及伪Zernike矩。

4.1 归一化中心矩

设大小为M×N的图像表示为f(x，y)，则图像的(p+q)阶原点矩定义为

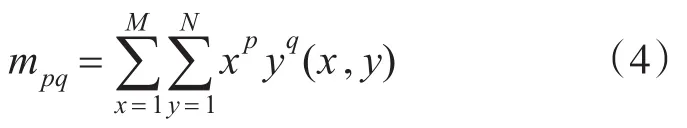
(p+q)阶中心矩定义为

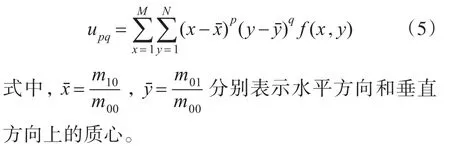
(p+q)阶归一化中心矩定义为

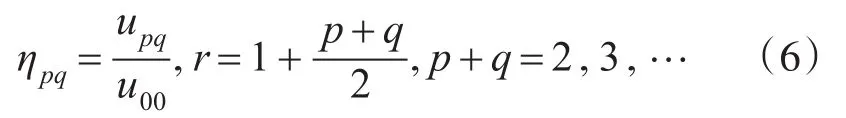
其中，u00表示图像面积，本文选用u11、u02、u12、u21、u03这五个中心矩特征，分别表示图像的倾斜程度、垂直方向上的伸展度、垂直方向上的均衡程度、水平方向上的均衡程度、垂直方向上的重心偏移度。

4.2 伪Zernike矩

伪Zernike矩是一种正交复数矩，对于连续函数f(x，y)，阶数为p，重复度为q的伪Zernike矩定义为

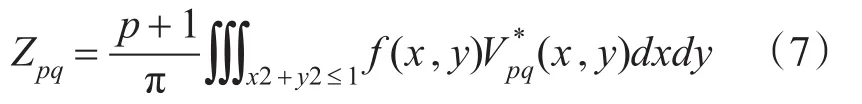
式中，p为非负整数，q为整数，且满足|q|≤p。*表示复数共轭，Vpq为伪Zernike多项式，表示为

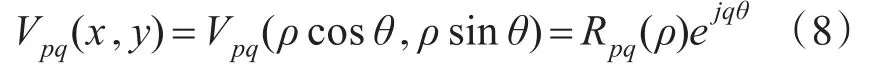
其中，实值径向多项式Rpq(ρ)用下式表示：

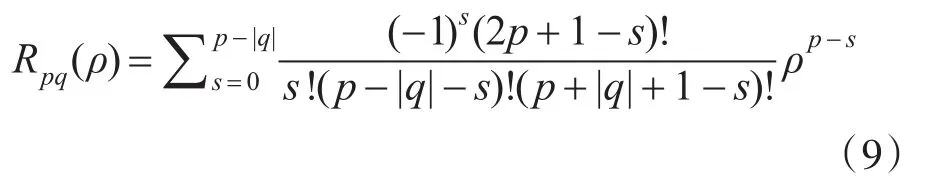
实际问题中处理的图像是数字图像，伪Zernike矩的离散形式为

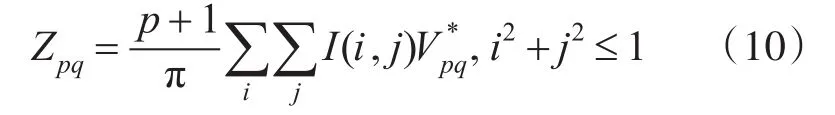
式中，I(i，j)是像素点 (i，j)处的像素。

为了减少伪Zernike矩的动态范围，本文对结果取对数，即pq=ln|Zpq|。并最终采用这7个伪 Zernike矩特征作为信号的识别特征。

综上，本文共选用12个形状特征，作为分类识别的特征。

5 仿真实验

为了验证本文算法的有效性，利用Matlab仿真了8种雷达脉内调制信号，分别是常规信号（CW）、线性调频信号（LFM）、非线性调频信号（NLFM）、二相编码信号（BPSK）、四相编码信号（QPSK）、频率编码信号（FSK）以及两种复合信号（FSK+BPSK复合、LFM+BPSK复合）。信号载频为400MHz、采样频率为1000MHz、脉宽10μs。线性调频信号的调频斜率为-8MHz/μs，二相编码和四相编码均为32位随机码。非线性调频信号为三阶多项式相位信号，多项式系数分别为15和-4。频率编码是2FSK信号，频点值分别是300MHz和330MHz，跳频序列是［1 0 1 0 1 1］，其中1代表频点330MHz，0代表300MHz。FSK+BPSK复合信号中FSK信号码元为300MHz和400MHz，跳频序列是［1 0 1 0］，其中1代表频点400MHz，0代表300MHz，BPSK为7位巴克码［1 1 1 0 0 1 0］。LFM+BPSK复合信号中LFM的调频率为-8MHz/μs，BPSK为13位巴克码［1 1 1 1 1 0 0 1 1 0 1 0 1］。

将信噪比从-8dB变化到12dB，每一类信号隔2dB生成300个样本，共生成26400个样本。其中，每一类信号每个信噪比下200个样本作为训练集，共计17600个样本；每一类信号每个信噪比下剩余的100个样本作为测试集，共计8800个样本。经过图像预处理，提取特征后，送入RF分类器，得到这8种信号的混淆矩阵如表1所示。

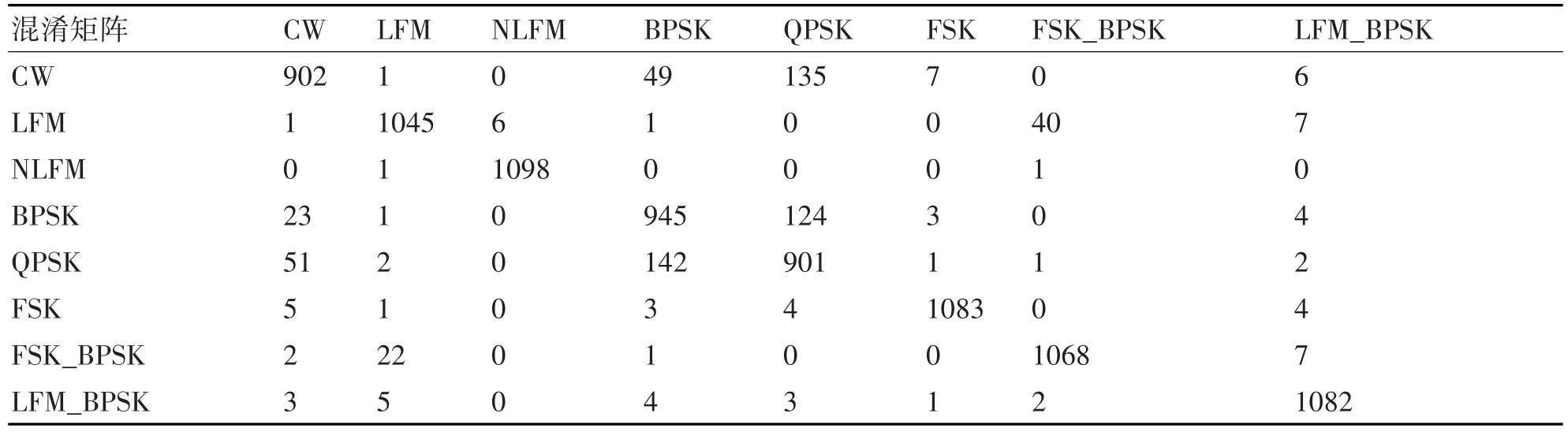
表1 混淆矩阵

每一种信号共有1100个样本，从表1可以看出，CW信号和相位编码信号容易相互识别错误，这是因为在信噪比较低时，三种信号的时频特征比较相像。这从第二节的时频图也可以看出，当信噪比较低时，受噪声的影响，二相编码和四相编码时频图上的跳变被湮没，容易识别错误；而常规信号由噪声引起错误的跳变，容易误识别为相位编码信号。除了这三种信号之外的其余信号的时频特征比较明显且不相似，识别结果均比较好。

为了更加清楚地说明本文算法的有效性，图4给出了每种信号在不同信噪下的正确识别率。

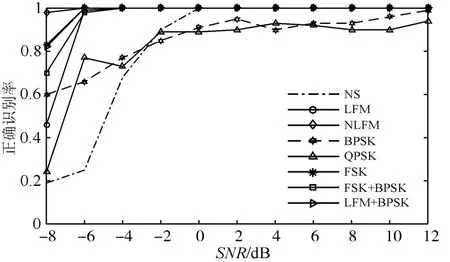
图4 正确识别率

从图4可以看出，在信噪比低至-6dB时，LFM、NLFM、FSK、FSK+BPSK、LFM+BPSK信号仍能达到98%以上的识别正确率；NS信号在信噪比大于-2dB时，识别正确率达到90%以上；BPSK、QPSK信号在信噪比不小于-2dB时，识别正确率大于85%；且随着信噪比的增加，所有信号的识别正确率大致也是上升的，BPSK和QPSK由于本身时频特征比较相像，且跳变特征没有很显著，导致有轻微的波动，但大体上识别正确率曲线还是随着信噪比上升的。

为了测试随机森林分类器的性能，本文分别利用随机森林、支持向量机（SVM）、K近邻（KNN）三种分类方法对时频特征不明显的相位编码信号进行分类识别。信号样本同上，在不同信噪比下的识别率如图5所示，可以看出，随机森林的识别准确率最高，明显优于SVM和KNN。

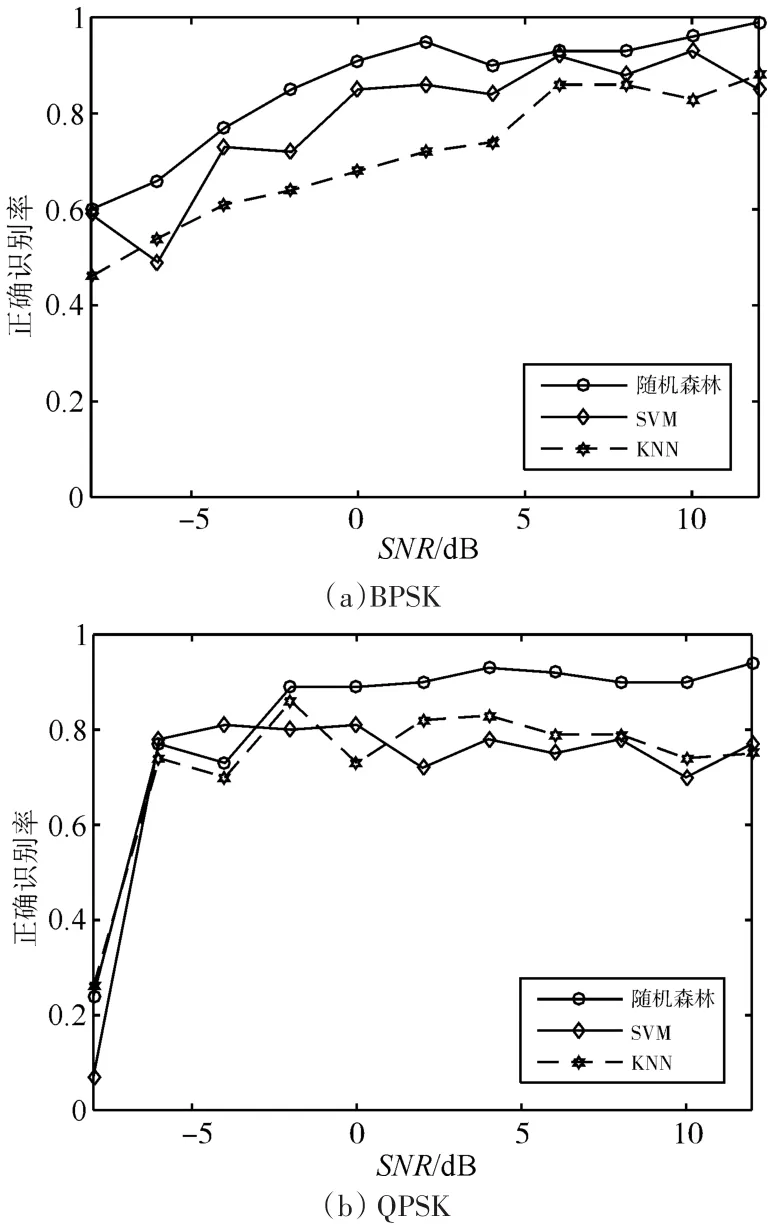
图5 不同分类器的分类结果

6 结语

本文针对雷达中复杂调制类型的识别问题，运用数字图像处理技术和形状特征理论，提出了一种对时频图像预处理后提取图像矩特征，再利用随机森林分类器识别的方法。对8种常见信号的仿真结果表明，本文算法在低信噪比下也能获得很高的识别准确率，具有较强的抗噪能力。并且对于目前比较复杂的复合调制类型，识别率也很高，具有一定的工程应用价值。