改进的蝴蝶算法优化粒子滤波算法研究*
2021-08-12杜先君韩晓矿
杜先君 韩晓矿
(兰州理工大学电气工程与信息工程学院 兰州 730050)
1 引言
在许多实际工程系统中,如目标跟踪、无线电通信、工业故障诊断和计算机视觉系统,物理模型通常是非线性的[1~2]。粒子滤波(PF)是一种基于蒙特卡罗方法的递推贝叶斯滤波算法,被认为是非线性非高斯状态估计的有用的工具之一[3]。近年来,PF在许多领域得到了广泛的应用[4]。然而,PF中粒子的贫化问题,降低了算法的性能[5]。粒子贫化问题是由于重采样过程不合理导致粒子多样性的匮乏。重采样过程中,高质量的粒子会被保留,而低质量的粒子会被舍弃[6]。虽然低质量粒子对状态估计的影响较小,但仍含有有用的粒子状态信息。因此,粒子的多样性丧失问题使得算法的性能大大降低。
许多学者在降低样品贫化的影响方面做了大量的工作。为了解决重采样步骤中遇到的粒子贫化问题,文献[7]在辅助粒子滤波器(APF)在中引入粒子索引作为重采样的附加变量。文献[8]中推导出一种精细的重采样算法,该算法分阶段比较粒子的权值,并基于拟蒙特卡洛方法构造新的粒子。上述方法着重于改进粒子滤波重采样过程,然而,样本贫化的问题并未完全解决。
近年来,集群优化算法的出现,为解决PF的粒子贫化问题打开了一扇新的大门[9]。在本文中,使用改进的蝴蝶优化算法(HBOA)来优化PF的重采样过程,提高PF算法的状态估计精度,解决PF算法的粒子贫化问题。
2 粒子滤波算法
粒子滤波算法是一种递归滤波算法,通过一组具有权重的随机样本来表示随机事件的后验概率,从含有噪声或不完整的观测序列,估计出系统的状态。
非线性系统的状态空间模型表示为
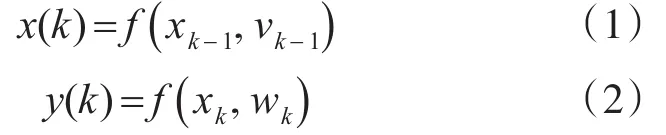
设状态初始概率密度函数为p(x0|y0)=p(x0),则状态预测方程为
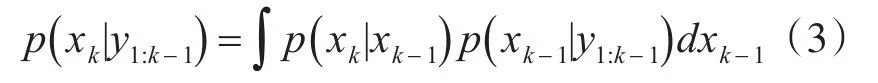
状态更新方程为
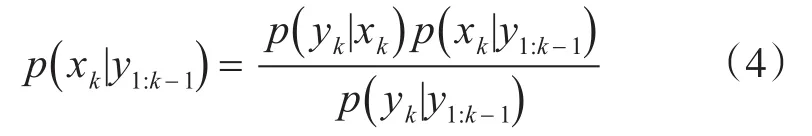
设重要性函数为q(x0;k|y1:k),将其改写为
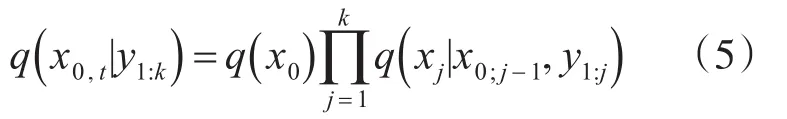
权值公式为
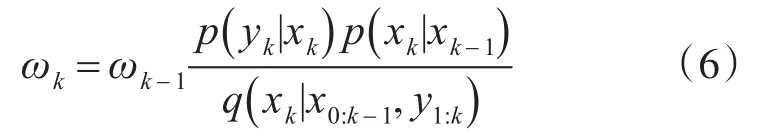
从p(xk-1|y1:k-1)中采样N个样本点,则概率密度为
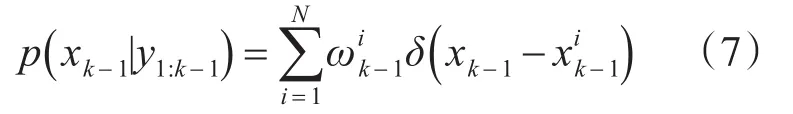
其中,δ(·)为狄拉克函数。
概率密度更新公式为
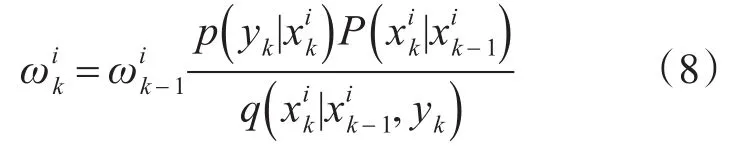
状态估计为

3 改进的蝴蝶优化算法
3.1 蝴蝶优化算法
Arora[10]提出了一种新的自然启发式算法—蝴蝶优化算法(Butterfly Optimization Algorithm,BOA)。在BOA中,每一只蝴蝶都会产生与蝴蝶的适应度相关的香味。当蝴蝶从一个地方移动到另一个地方时,它的适应能力也会随之改变。这种香味会向蝴蝶的四周分散出去,使得其余的蝴蝶可以通过感官嗅到它。这样,蝴蝶群中的蝴蝶通过散发各自的香味来共享各自间的信息。当一只蝴蝶能够感觉到任何其他蝴蝶的香味时,它就会向其他蝴蝶移动,进行全局搜索。当一只蝴蝶感觉不到香味时,它就会在空间中自由飞行,进行局部搜索。
由上述叙述,可将蝴蝶的行为理想化如下特征。
1)所有的蝴蝶都可以散发能吸引其他个体的香味。
2)每只蝴蝶有两种运动方式:随机飞行或者朝向香味强度最高的蝴蝶飞行。
3)蝴蝶的刺激强度由目标函数决定。
在BOA中,每个蝴蝶个体都有着独特的香味和个体感知能力,体现出BOA算法与其他智能优化算法的不同。蝴蝶个体散发的香味强度数学公式如下:

其中,f为感知到的香味大小,即蝴蝶感知香味的强弱;c为感官因子,通常取0.01;I为刺激强度,与适应度值有关;a为依赖于形态的指数,通常取0.1。说明蝴蝶对香味的吸收程度不同。
在算法的初始阶段,随机产生蝴蝶的位置,由式(10)计算蝴蝶在各自为位置产生的香味,然后算法进入全局寻优和局部寻优阶段。在全局寻优阶段,蝴蝶个体朝向香味最强的蝴蝶g*飞行,可以表示为
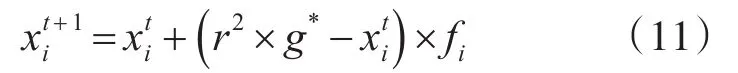
局部寻优阶段可以表示为
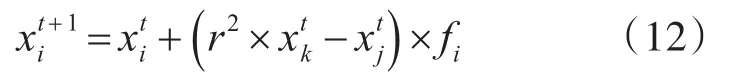
其中,xj和xk是从寻优空间中选取的第j和第k个蝴蝶。r是[0,1]之间的随机数。
通常蝴蝶寻找食物可以在局部和全局范围内发生,可通过设置切换概率p来决定它的飞行方式,通常取为0.8。
3.2 蝴蝶优化算法的改进
针对标准BOA算法存在的依赖初始种群、容易误入局部最优和后期寻优速度低等问题,本文从两个方面对蝴蝶算法进行了改进。首先通过引入对立学习策略对蝴蝶种群进行优化处理;然后通过引入自适应权重因子来调节蝴蝶算法的全局寻优与局部寻优过程,提高它的寻优性能。基于以上两种策略,本文提出了混合蝴蝶优化算法(Hybrid BOA,HBOA)。
1)对立学习策略初始化种群
基本的BOA算法在寻优前期采用随机化的方法产生蝴蝶个体,使得蝴蝶的初始种群不具有全局最优的信息。对于蝴蝶优化算法而言,其寻优的基本策略为将前代产生的优秀个体保留到下一代中,循环地进行优中选优,最终得到最优个体。若种群中优秀蝴蝶个体较少,则会影响算法的快速性和准确性。因此本文将对立学习策略应用到蝴蝶种群的初始化进程中,提高算法的寻优性能。
对立学习(opposition-based learning,OBL)是由学者Tizhoosh在2005年首次提出的概念[11]。其主要思想是在一定的空间内,对当前的可行解产生对应的对立解,然后同时对可行解和对应的对立解进行评估,挑选之中的高质量个体代替当前的可行解。
设在定义域[l,u]上存在数x,则数x的对立点为x′=l+u-x。将定义域扩展到n维空间,设p=(x1,x2,…,xn)为n空间的一点,其中xi∈[li,ui],i=1,2,…,n,则其对立点为,其中[11]。
由定义可对蝴蝶初始种群进行对立学习策略处理。
(1)在优化空间中,随机初始化N个蝴蝶的位置,N为蝴蝶个体数量。
(2)产生N个蝴蝶的对立个体,表示为。
(3)将两个种群进行合并,并求取个体适应度值,对其排序并取最优的前N个个体作为初始化种群。
2)自适应惯性权重
惯性权重最早是由Shi在1998年提出的,用来调节优化算法的全局寻优和局部寻优能力[12]。当惯性权重较大时,算法的全局寻优能力较强,使得算法能够寻找新的未知区域,增加解的多种可能性;当惯性权重较小时,算法具有较强的局部寻优能力,使得搜索精度变强。该策略已被许多学者用于改进群体优化算法。
受此启发,本文将惯性权重应用到BOA的全局寻优中,提高算法的寻优性能。自适应惯性权重随着算法循环次数的上升呈现下降趋势,其设置如式(3)所示:
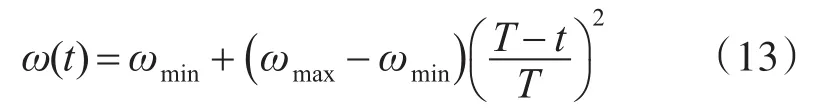
其中,ωmax为迭代初始阶段的惯性权重,ωmin为迭代结束时的惯性权重,T为算法运行的最大迭代次数,t为当前运行的迭代次数。惯性权重ωmax取0.9,ωmin取0.5时,算法具有最佳的性能。
此时,算法的全局搜索可表示为
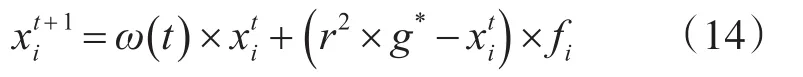
4 基于HBOA的PF
HBOA优化PF的思想是粒子作为初始的蝴蝶个体,通过目标函数分别计算蝴蝶个体的适应度值,得到蝴蝶个体的香味浓度,然后将香味浓度最高的蝴蝶个体选为最优值。通过选择概率来确定蝴蝶个体进行全局寻优还是局部寻优。经过一定的迭代次数,使得蝴蝶种群向最优的位置靠近,最终取得全局最优值。这样,粒子集会不断的高似然区靠近,使得滤波算法性能得到提升。
设置蝴蝶个体的香味刺激强度表示为
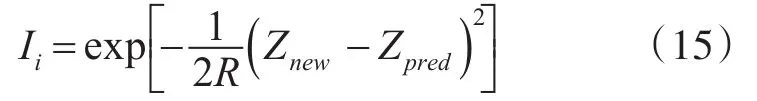
式中,R为观测噪声的方差;Znew为最新观测值;Zpred为预测的观测值;Ii为刺激强度。
综上,HBOA-PF步骤如下。
步骤1:参数初始化。设置HBOA的寻优代数max,设置蝴蝶个体数为N;设置切换概率P,设置滤波步数T。
步骤2:算法初始时,从先验信息中采样N个粒子作为算法的初始粒子。
步骤3:模拟HBOA算法,指导粒子移动。
1)使用对立学习方法处理蝴蝶样本。
2)然后根据式(15)计算所有蝴蝶个体的刺激强度,由式(10)计算蝴蝶个体的香味浓度,选取香味浓度最强的最为全局最优解。
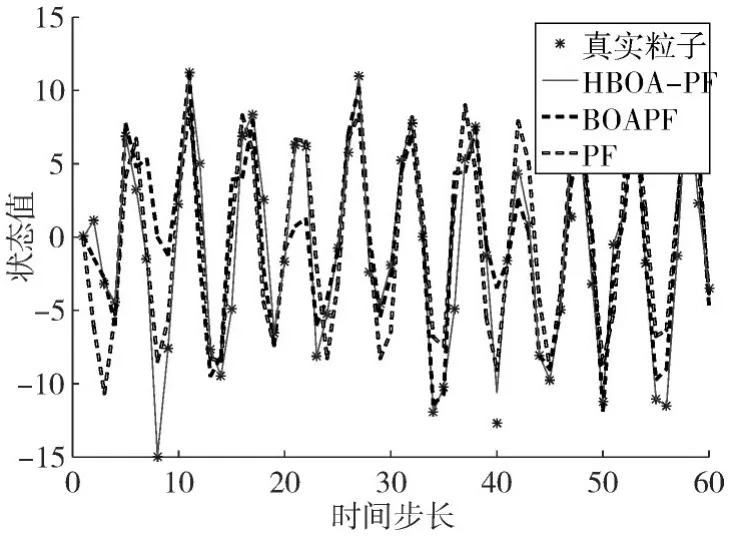
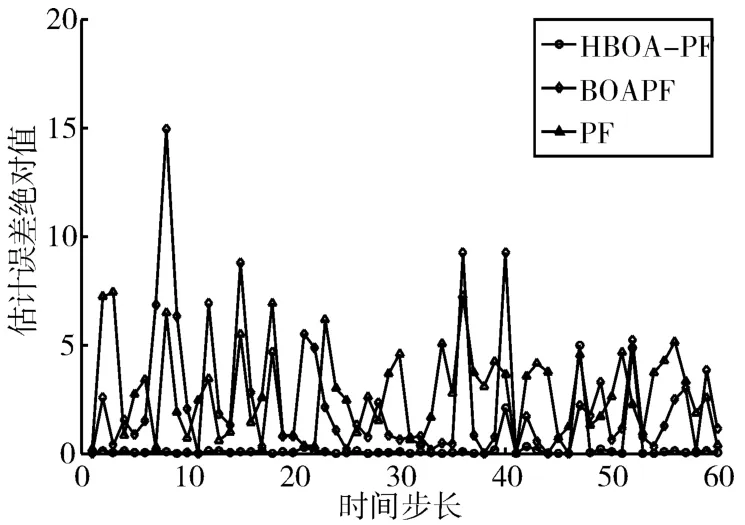
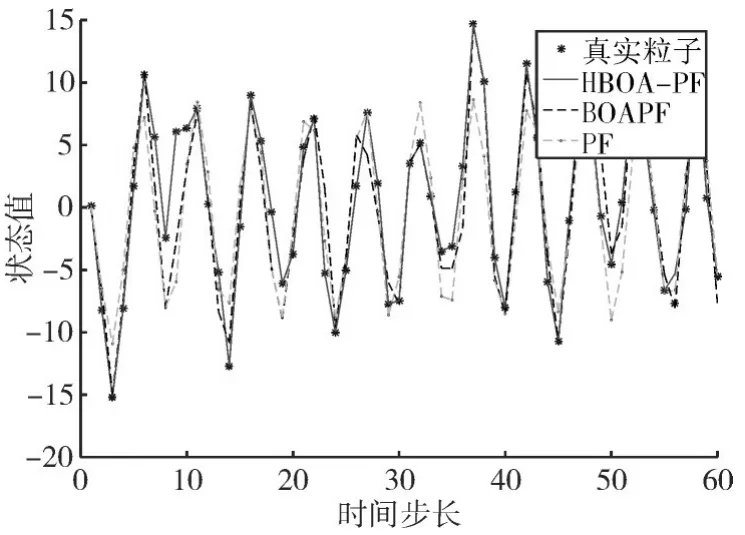
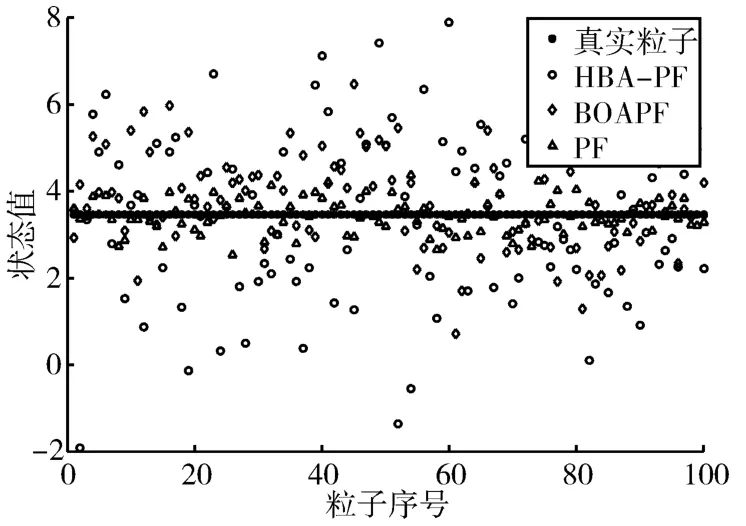
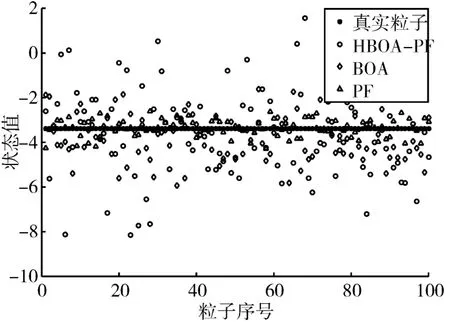
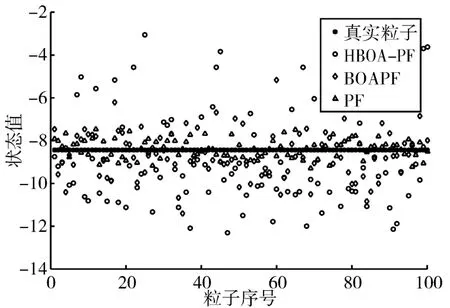
3)若转换概率p>rand,则按式(14)进行全局寻优,更新蝴蝶位置,若转换概率p 步骤4:满足最大寻优次数时,结束优化,否则跳转到2)中。 步骤5:计算粒子权值并归一化。 步骤6:状态估计: 步骤7:输出滤波结果。 为了验证把本文提出算法的性能,将其与PF和BOAPF[13]相比较,本文选取测试模型的数学表达式如下: 式中,w(t)和v(t)为零均值高斯噪声,设系统噪声w(t)的方差为Q=10,测量噪声v(t)的方差为R=1,仿真步长T设置为60,初始化蝴蝶种群数量N=50,惯性权重ωmax取0.9,ωmin取0.5,感官因子c取0.01;形态指数取0.1。均方根误差计算公式为 1)当粒子数N=20,Q=10,仿真结果如图1和图2所示。 图1 系统状态估计(N=20,Q=10) 图2 估计误差绝对值(N=20,Q=10) 2)当粒子数N=100,Q=10时,仿真结果如图3、图4所示。 图3 系统状态估计(N=100,Q=10) 由图1~4可知,随着粒子个数的增加,三种算法的状态估计结果都有显著的改善,但本文算法的状态估计精度更高,估计误差更小。 选取粒子数N=100,Q=10,对k=10、k=25、k=50的粒子分布多样性进行研究,仿真结果如图5~7所示。 图5 k=10时的粒子状态分布图 图6 k=25时的粒子状态分布图 图7 k=50时的粒子状态分布图 从图5~7可以看出,相对于PF,BOAPF和HBOA-PF在粒子迭代过程中对粒子的多样性都有改善,但HBOA-PF的对粒子的多样性提升更加显著。 本文提出了一种改进蝴蝶算法优化粒子滤波算法,通过加入对立学习策略和自适应权重策略,增加了种群的多样性,提高了算法的状态估计精度。选取非线性系统为仿真对象,对PF、BOAPF和本HBOA-PF进行对比,结果表明本文提出的算法状态估计能力更强,精度更高,并选取k=10、k=25、k=50的粒子状态分布进行测试,结果显示本文算法的粒子多样性更加丰富。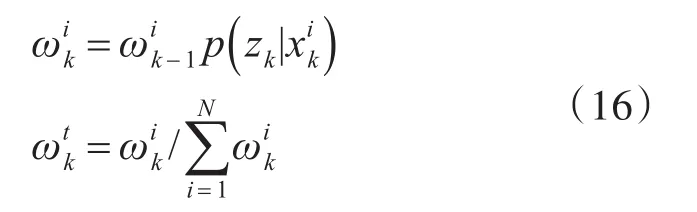

5 仿真实验分析
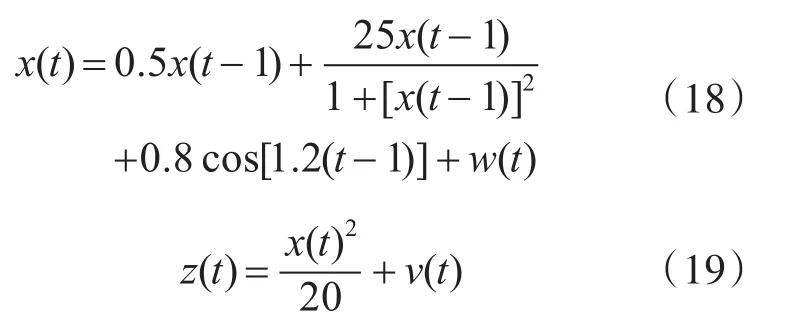
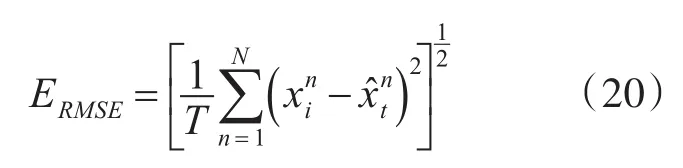
5.1 状态估计精度测试
5.2 粒子多样性测试
6 结语
