弹道目标的变结构多模型数据滤波方法*

黄晶晶 陈世友

（武汉数字工程研究所 武汉 430074）

1 引言

随着弹道导弹的发展，弹道导弹防御技术［1］的研究也愈加受到重视，弹道目标数据滤波技术是弹道导弹防御的核心技术之一，对导弹落点预测的准确度和弹道导弹拦截的成功率至关重要［2］。根据弹道导弹运动过程中的受力情况，可将其弹道分为主动段、自由段和再入段三个飞行阶段。由于各阶段运动特征差别较大，单模型弹道目标数据滤波方法不能实现对全弹道的连续估计。使用交互多模型算法可以解决上述问题，但也存在一些缺点，交互多模型算法的估计性能与所选模型集密切相关［3～4］，而模型集的选择通常处于两难的境地，为提高估计精度需要尽可能多地增加模型的数量，而过多的模型会增加模型之间的竞争并且增加计算量，导致估计精度降低。另外，由于弹道目标各阶段的运动特征明显不同，每个阶段均使用所有模型来滤波会增加不必要的计算量。

为克服上述缺点，本文基于变结构多模型算法［5］，提出了一个适用于弹道目标全阶段的滤波方法。该方法采用多模型的结构，相较于单模型跟踪算法，可用于跟踪任意阶段的弹道目标；相较于交互多模型算法，可以减少不必要的计算，同时提高精度。本文基于三个不同阶段分别建立运动模型，每个阶段对应一个变结构多模型的滤波器。其中，主动段采用Singer模型［6］和重力转弯模型［7］两种模型的交互输出作为主动段滤波器的输入，自由段采用椭球体地球重力模型［8］，再入段采用基于椭球体地球重力模型和空气阻力模型的运动模型［9～10］。各阶段运动模型都建立在混合坐标系［10］下，在雷达站坐标系下建立弹道目标各运动阶段的状态方程，在雷达站球坐标系下建立各运动阶段的量测方程。本文基本滤波算法采用扩展卡尔曼滤波（EKF）算法［11］。

2 弹道目标运动模型

本文根据各阶段受力情况应用了不同的运动模型，由于各阶段运动模型的状态变量的维度不同，无法直接用于变结构多模型算法中模型的交互，所以将各个状态变量分为包括目标位置和速度的六维主状态变量和包括其他状态变量的次状态变量，主状态变量用于多模型之间的交互，次状态变量仅在滤波器内部循环。本文中所有运动模型都建立在混合坐标系下，在雷达站坐标系下建立弹道目标状态方程，在雷达站球坐标系下建立量测方程。

2.1 主动段运动模型

主动段主要受到发动机推力、地球重力和空气动力的作用。使用Singer模型和重力转弯模型分别描述该阶段的运动情况，运动模型分别如下。

2.1.1 Singer模型

设弹道目标Singer模型［12］的状态变量如式（1），各变量依次表示目标在各个方向的位置、速度和加速度。

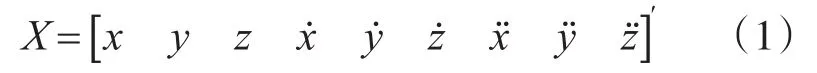
Singer模型在雷达站坐标系下的状态方程为

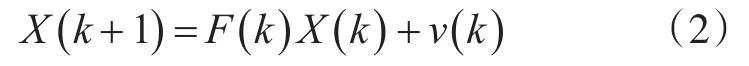
将式（1）的状态向量分离为主状态向量X1和次状态向量X2：

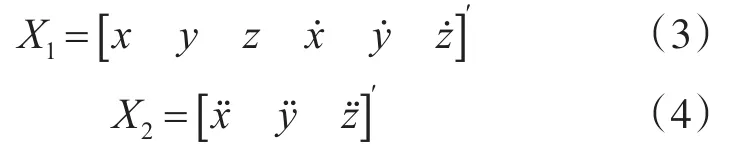
该运动模型中其他矩阵向量参考文献［12］。

2.1.2 重力转弯模型

设弹道目标的状态变量为

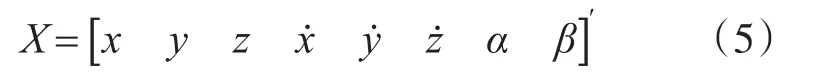
弹道目标在雷达站坐标系下的状态方程如式（8）所示，式中各变量含义为，其中T表示发动机推力，D表示空气动力，m表示弹道目标质量；β=δm/m，其中δm>0，表示导弹质量减小的速率；μ=3.986005×1014m3/s2，为地球重力常数；Reh=rem+h，rem=6371010m，为地球半径，h为雷达站的大地高程。

速度v和位移r0表达式如下：

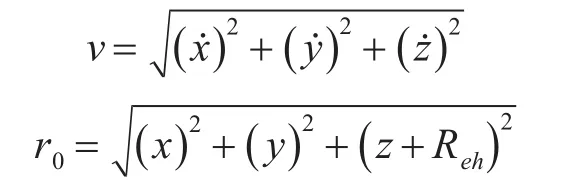
对状态方程进行泰勒级数展开并忽略高阶项有：

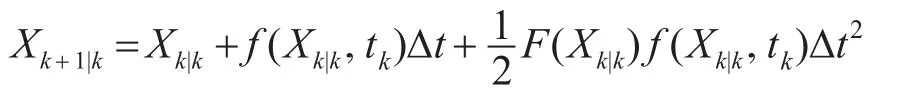
状态方程的雅可比矩阵求解公式为

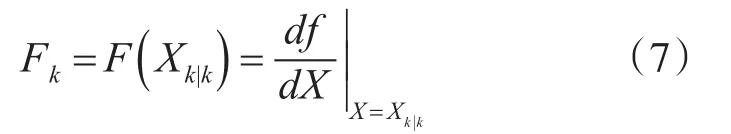
将状态向量分离为主状态向量X(1)和次状态向量X(2)，表达式如下所示：

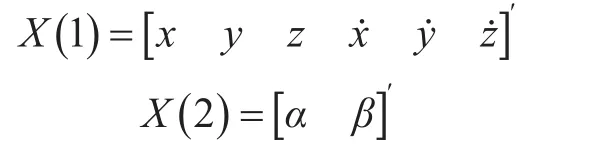
将状态方程、泰勒级数展开的函数和雅可比矩阵也相应分离，分别在滤波器内迭代计算。

2.2 自由段运动模型

自由段是指弹头从头体分离到再次进入大气层的一段弹道，这一阶段目标近似于在真空中运动，可认为仅受到地球重力的作用，为使运动模型更接近真实情况，地球重力采用椭球地球模型。

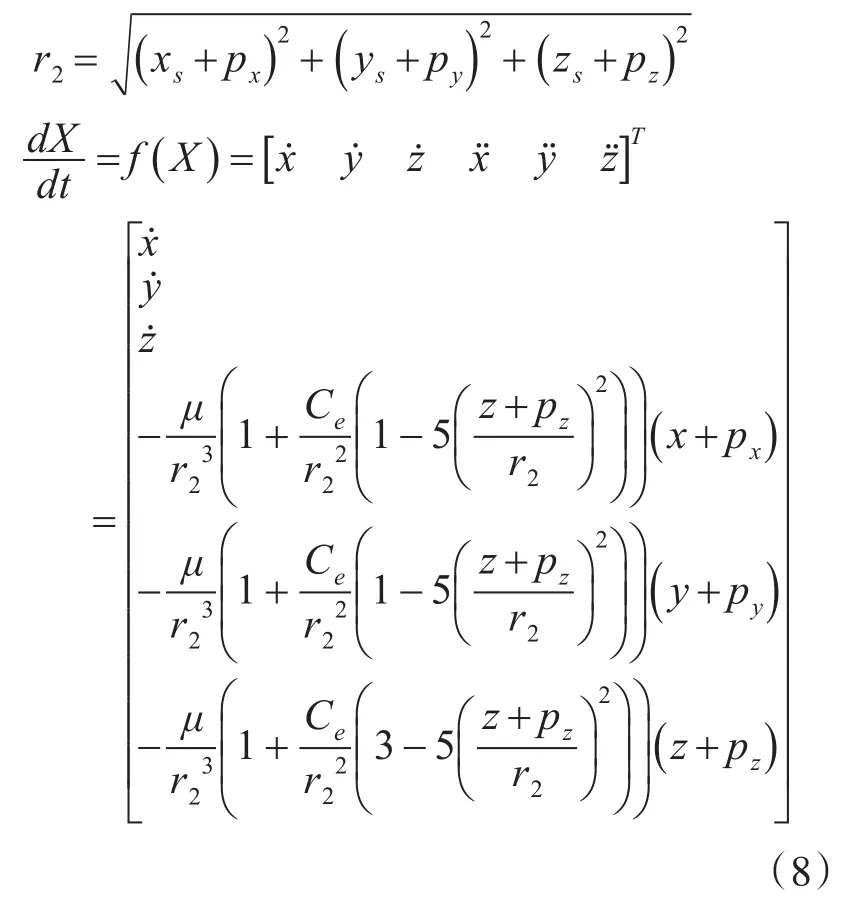
状态方程的雅可比矩阵求解公式与式（7）相同。

2.3 再入段运动模型

再入段是指弹头从再次进入大气层到落地为止的一段弹道，这一阶段弹头除受到地球重力之外还受到巨大的气动阻力。因此，将气动阻力α增广到状态向量中得到表达式如下：

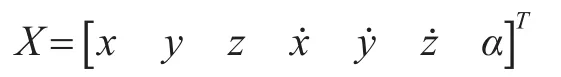
雷达站坐标系下再入段弹道目标的状态方程为

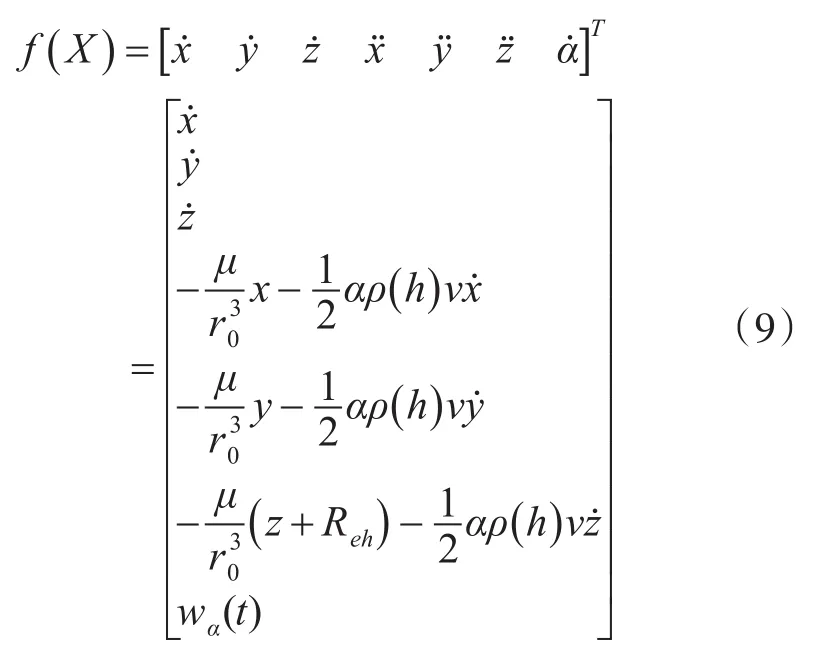
式中，α表示阻力参数，ρ(h)=ρ0e-kh为空气密度函数，其中ρ0=1.22kgm-3。

对上式进行泰勒级数展开并忽略高阶项有：

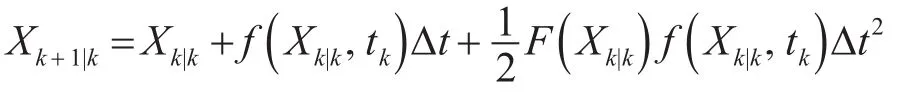
状态方程的雅可比矩阵求解公式与式（7）相同。

将状态向量分离为主状态向量X(1)和次状态向量X(2)，表达式如下所示：

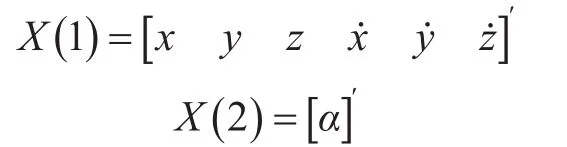
对状态方程、泰勒级数展开的函数和雅可比矩阵的处理与主动段中的重力转弯模型相同。

3 雷达量测模型

状态向量在雷达站坐标系下描述，量测值在雷达站球坐标系获取，其中R为距离，A为方位角，R为俯仰角。则用状态变量表达的量测方程如下：

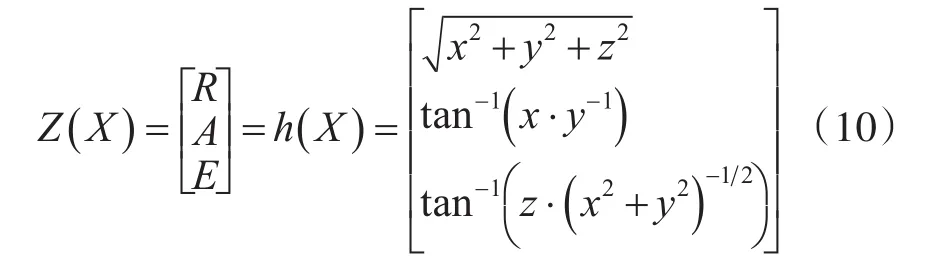
对上式进行泰勒展开并忽略高阶项有：

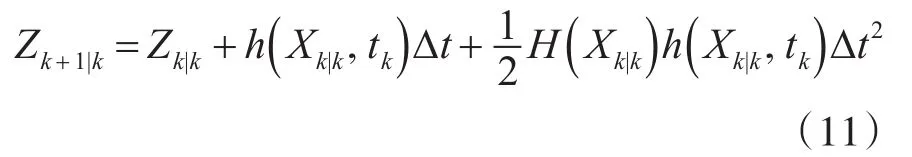
式（11）中H(Xk|k)为量测方程的雅可比矩阵，表达式如下：

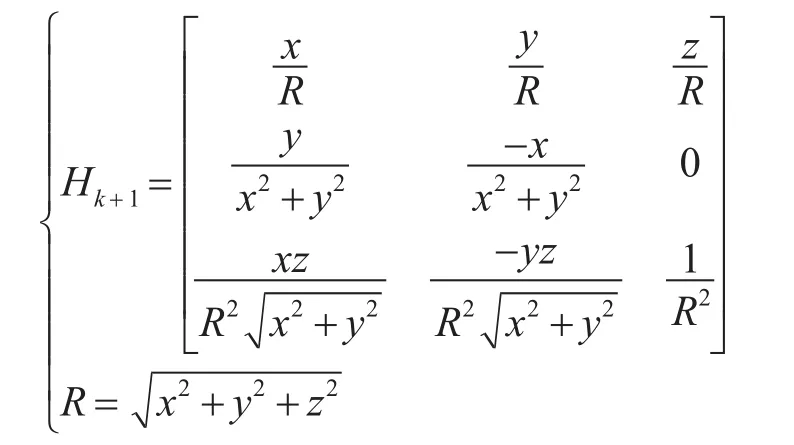
4 弹道目标的变结构多模型算法

模型集切换算法是变结构多模型的一种模型集自适应算法，该算法的优势是模型集之间的切换通过两阶段进行，在激活候选模型集后不立刻终止当前模型集，而是运行二者的并集直至当前模型集达到设定的终止条件。这种切换方式可以有效地避免虚假切换。本文在模型集切换算法的基础上，设计了一个适用于弹道目标全阶段的数据滤波方法，相较于单模型跟踪算法，该算法可用于跟踪任意阶段的弹道目标。该方法的一个周期由以下七个步骤组成。

1）设计模型集的覆盖。弹道目标主动段是整个飞行阶段受力最复杂的阶段，为了更准确地对主动段数据滤波，本文采用Singer模型和重力转弯模型的交互多模型算法描述该阶段运动情况，两个模型分别用m1、m2表示；弹道目标自由段在三个运动阶段中受力情况最简单，运动轨迹可预测性更强，该阶段采用椭球体地球重力模型，用m3表示；弹道目标再入段主要受到地球重力和空气阻力的作用，采用基于椭球地球模型和空气动力模型的运动模型描述，用m4表示。

2）设计候选模型集。模型集的设计与整体模型集合以及它们的拓扑紧密相关。由各个模型代表的系统模式很接近时，这些模型可以聚成一个模型集。弹道目标飞行所经历的运动阶段依次为主动段、自由段和再入段。设计各个阶段模型集的集合为C={M1，M2，M3}。其中，M1={m1，m2}，为主动段模型集；M2={m3}，为自由段模型集；M3={m4}，为再入段模型集。

3）判断弹道目标当前飞行阶段。当雷达探测到弹道目标的数据时，首先要做的事情是判断弹道目标当前处于哪个阶段。初始模型集的激活只能依靠从量测序列中获得的后验信息，通过后验信息总结出模型概率和似然，从而判断当前弹道目标处于哪个运动阶段。初始模型集的激活需要同时满足以下两个条件：

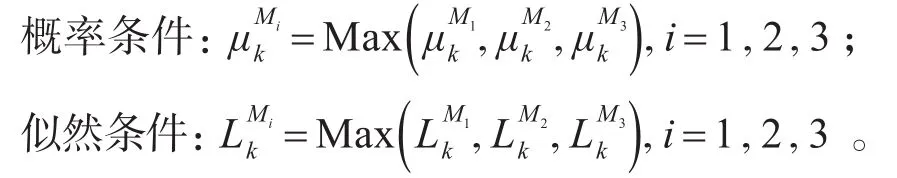
其中，模型集概率是k时刻基于计算的模型集中所有模型的概率之和；模型集似然为k时刻模型集中模型的所有（边缘）似然的概率加权和。

4）时间计数k增加1，运行变结构交互多模型算法递归周期［13］。

5）判断是否激活候选模型集。如果是，则进入下一步；如果不是，则输出从变结构交互多模型算法周期获得的目标状态估计值k|k、状态误差协方差Pk|k和模型概率，返回4）。

设Mk为当前运行的模型集，当候选模型集Mk+1同时满足以下两个条件时，激活Mk+1。

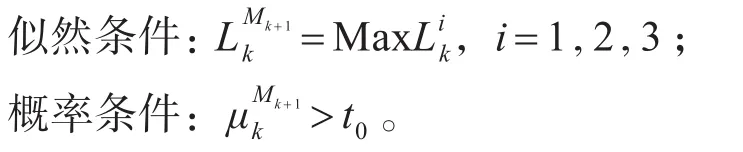
t0为该激活逻辑中的门限值。

6）如果有候选模型集被激活，下一时刻的模型集变为当前时刻运行的模型集M0和新激活的候选模型集Ma的并集Mk，并且运行变结构交互多模型算法的一个周期。

（1）计算并集Mk的模式概率、状态矩阵和误差协方差矩阵。

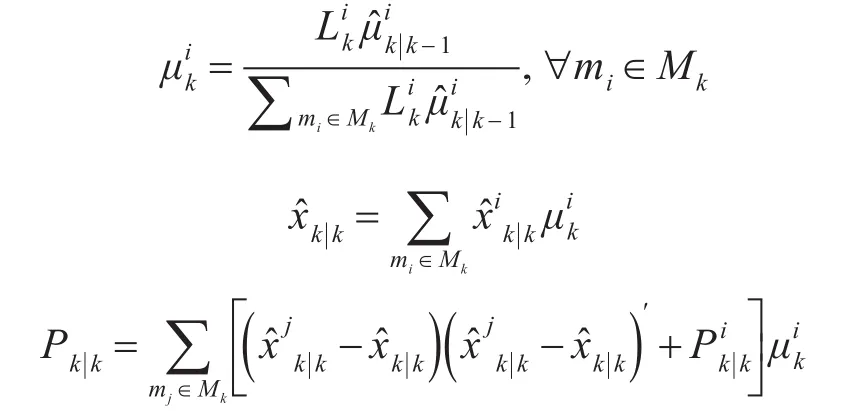
（2）判断是否终止模型集M0和Ma，对模型集Ml=Mo，Ma计算下列模型概率和模型似然。

7）选择模型转移概率矩阵。综合考虑弹道目标的飞行特性，定义模型转换矩阵如下：

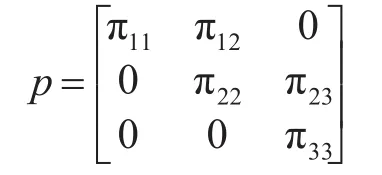
模型飞行阶段切换示意图如图1。

图1 弹道目标飞行阶段模型转换图

5 仿真结果

以某两级弹道导弹为仿真对象，假设发射点的大地坐标为(130°E，30°N )，发射方位角为 40°。仿真后弹道目标的落点大地坐标为(95°W，29°55′N )。假设雷达站位于地球表面，大地坐标为(95°W，30°N )。设定量测向量的距离量测方差为1m，方位角和俯仰角的量测方差均为10-3rad，跟踪数据率为1Hz。将本文提出的基于变结构多模型数据滤波算法与单模型EKF算法进行对比分析，采用位置和速度的均方根误差（Root-Mean-Square Error，RMSE）作为标准对比分析滤波效果。

5.1 主动段仿真结果对比

从图2和图3主动段的弹道目标数据滤波算法的估计精度对比可以看到，基于变结构多模型算法的数据滤波方法的位置和速度的RMSE都优于基于EKF算法的单模型数据滤波方法，在50s左右变结构多模型算法逐渐收敛，而另外两种单模型算法的误差值仍然是波动上升的趋势。从表1可以得出，变结构多模型算法与基于Singer的EKF算法的位置误差和速度误差的比值分别为0.803和0.787，与基于重力转弯模型的EKF算法的位置误差和速度误差比值的分别为0.835和0.673。

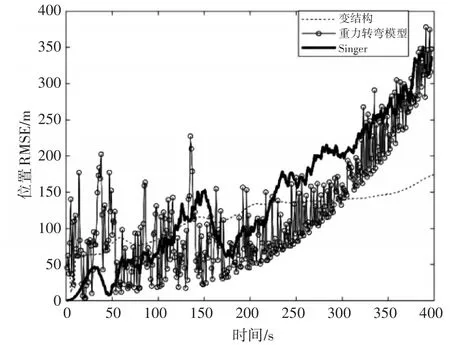
图2 主动段的位置均方根误差对比

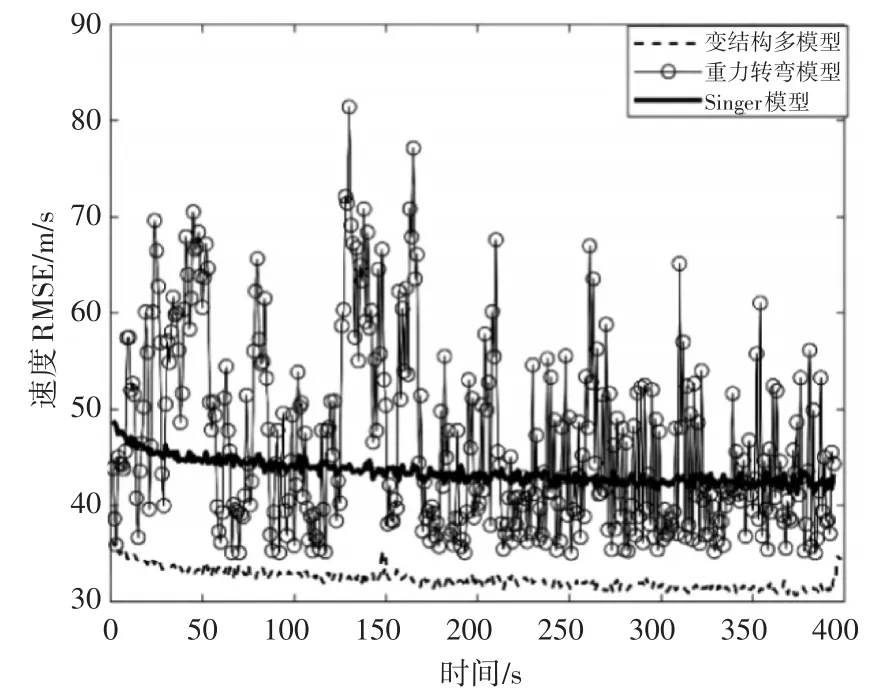
图3 主动段的速度均方根误差对比

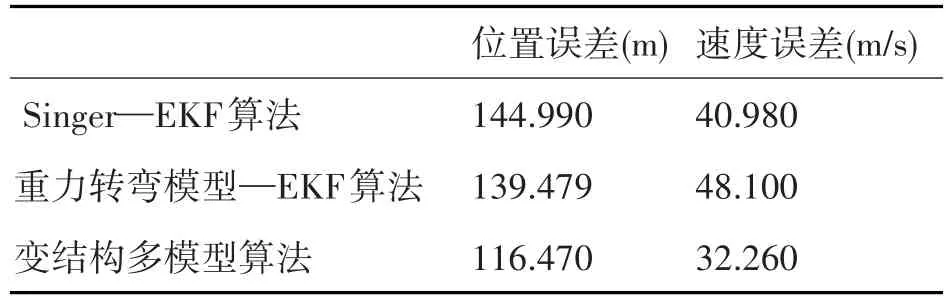
表1 主动段的均方根误差均值对比

5.2 自由段仿真结果对比

从图4和图5自由段的弹道目标数据滤波算法的估计精度对比可以看到，基于变结构多模型算法的数据滤波方法的位置和速度的均方根误差都优于基于EKF算法的单模型数据滤波方法，在50s左右变结构多模型算法逐渐收敛，而EKF单模型算法在200s时才逐渐收敛。从表2可以得出，变结构多模型算法与EKF算法的位置误差和速度误差比值的分别为0.601和0.654。

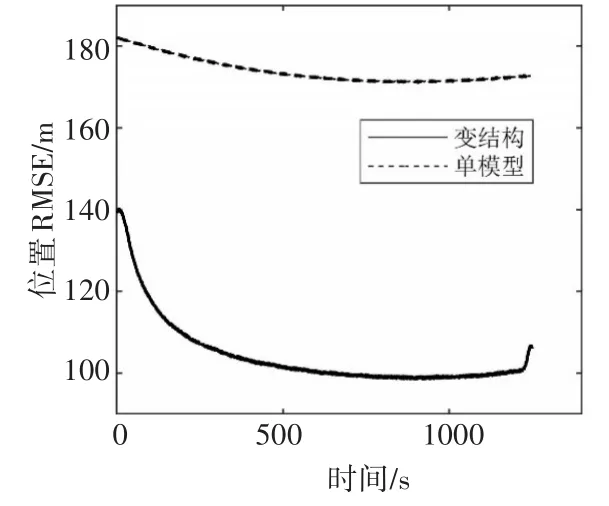
图4 自由段的位置均方根误差对比

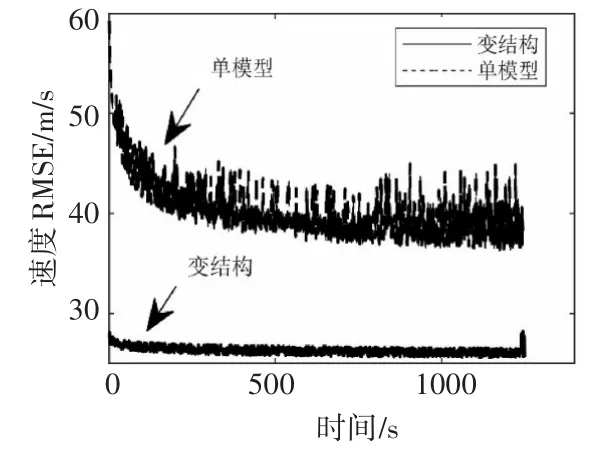
图5 自由段的速度均方根误差对比

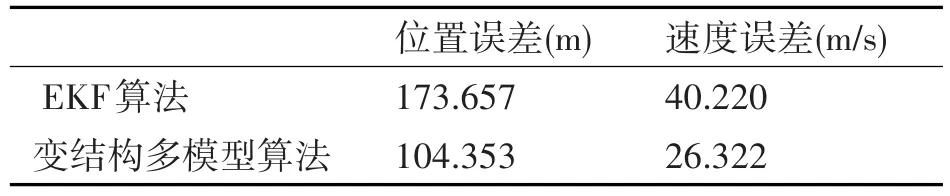
表2 由段的均方根误差均值对比

5.3 再入段仿真结果对比

从图6和图7再入段的弹道目标数据滤波算法的估计精度对比可以看到，基于变结构多模型算法的数据滤波方法的位置和速度的均方根误差都优于基于EKF算法的单模型数据滤波方法，在20s左右变结构多模型算法逐渐收敛，而另外两种单模型算法的误差值仍然是波动上升的趋势。从表3可以得出，变结构多模型算法与EKF算法的位置误差和速度误差比值的分别为0.536和0.740。

表3 再入段的均方根误差均值对比

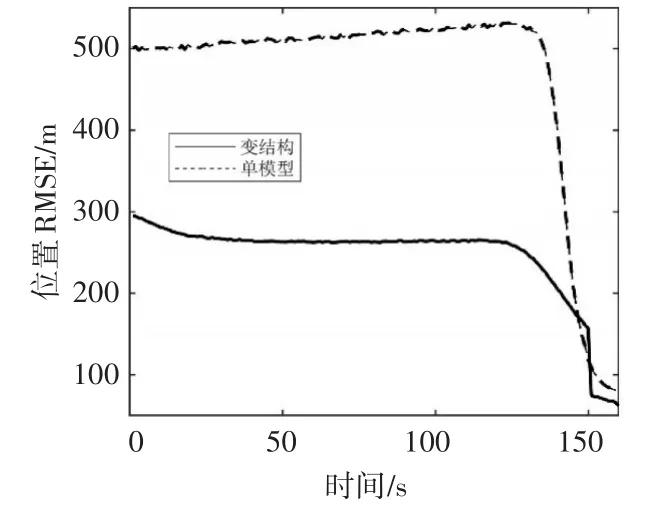
图6 再入段的位置均方根误差对比

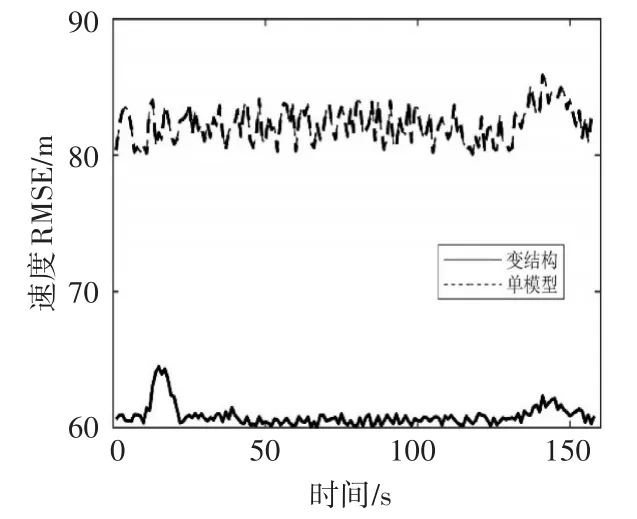
图7 再入段的速度均方根误差对比

6 结语

本文提出了一种基于变结构多模型算法的弹道目标数据滤波方法，可以实现对弹道目标全弹道的数据滤波。通过仿真实验得出，与基于单模型的EKF算法相比，本文所提方法有以下优势：各运动阶段的位置和速度均方根误差均值都更小，即该算法估计精度更高；当滤波数据出现波动时，本文方法在各运动阶段的收敛速度都更快，即该算法更稳定；在主动段和自由段、自由段和再入段的交替处基于变结构多模型算法的弹道目标数据滤波方法的均方根误差值抖动范围更小，抖动时间更短，这表明该算法在弹道目标出现机动时能够更快适应。