基于EEMD及能量变化曲线的配电网故障选线

2021-08-11宏爱松李艳丰刘保辉

东北电力技术 2021年6期

宏爱松，李艳丰，刘保辉

(保定市毅格通信自动化有限公司，河北保定 071000)

电力系统根据中性点接地方式的不同，分为有效接地方式和非有效接地方式，非有效接地方式主要包括中性点不接地、中性点经消弧线圈和中性点高阻接地[1-6]。目前，除美国的中压配电网使用大电流接地方式外，世界其他各国的中压配电网系统普遍使用小电流接地方式，在我国3～66 kV的中压配电网一般均采用非有效接地方式[1]。其中66 kV和35 kV配电网系统多数使用消弧线圈接地，3～10 kV配电网则采用中性点不接地系统为主。由于我国配电网结构复杂，分支众多，面积广阔，所以故障率较高,其中以单相接地故障尤为突出。据统计,单相接地故障约占故障总数的80%以上。由于中性点采用非有效接地运行方式，当配电网发生单相接地故障时,不会形成短路回路,接地故障相电流仅由系统的分布电容引起，此时系统的线电压依然保持对称，仍可以保持电网负荷的正常供电, 继电保护装置不会马上动作，所以系统可以带故障运行一段时间,这就避免了突然中断供电对用户造成影响。但由于此时健全线路相对地电压升高到了原来的线电压，增加了对线路绝缘性能的要求，容易在健全线路发生对地闪络[7-9]，而造成更严重的接地短路，危害更大。如果此时电气人员可以在2 h内确定故障点并加以排除，电网就可以连续运行，提高系统供电可靠性，这也是中性点非有效接地系统的最大优势。然而故障如不及时排除，可能会造成故障规模扩大，进而导致系统崩溃。为此，迅速而有效地选出故障线路并判断故障点位置对提高供电可靠性意义十分重大。系统发生单相接地故障时，达到稳态后，故障电流一般小于20 A，若发生高阻接地，则故障信号会更加微弱。则选线中用到的有功分量和谐波分量幅值会更小，在复杂的电力系统的电磁环境下，这些特征量受到电磁干扰，会给选线带来一定的误差。同时配电网结构复杂，常常根据负荷的变动，改变其接线形式，所以对于不同的电网结构，故障特征量有时比较明显有时不明显。而利用暂态特征量，由于暂态过程持续时间很短，故障特征量也很难捕获。大部分选线方法是基于零序电流选线的，而当系统发生接地故障时，故障线路与健全线路的判别特征量的差异不是很明显时，由于零序电流互感器的测量误差，给选线造成了困扰。同时线路的不平衡电流也会影响测量的准确性。单相接地故障中，大部分为间歇性接地或瞬时接地，即故障处多为电弧接地，由于电弧的非线性特性，给选线造成了一定影响。另外由于配电网运行方式的频繁改变，变电站的出线数量与长度也是不断改变，则电容电流和谐波电流也不断变化的[10-14]。

目前主要的方法大致可以分为基于稳态量的方法、基于暂态量的方法和两者融合的选线法。当系统发生故障后，由于电容充放电的影响会产生丰富的电气暂态量，因此暂态量的方法得到了学者们的广泛关注。

EEMD算法是一种自适应的信号分析方法，它能够通过数据自身的时间尺度特征来进行信号按照频率的分解，且无须预先设定任何基函数。EEMD算法是通过对原始多次加入白噪声之后再进行EMD分解，将所得结果平均得到各个固有模态函数，EEMD算法抑制了EMD算法的模态混淆问题，通过EEMD算法对信号分解，可以得到从高频到低频的固有模态函数，并且所得结果相比于EMD算法更具有实际意义。用EEMD算法对故障后各线路零序电流分解，计算各线路第一固有模态的能量曲线，构建选线信息度函数，通过其值大小准确选择故障线路，通过ATP-EMTP完成仿真试验，验证所提方法的准确性。

1 集合经验模态分解算法

由于EMD算法处理暂态信号时会受到突变干扰，出现模态混淆问题，使所得的固有模态函数分量失去信号本身的物理意义。而EEMD算法通过添加不同的高斯白噪声和多次集合平均克服了EMD的模态混淆问题。具体步骤如下。

a.在信号S(t)叠加高斯白噪声h(t)，其中高斯白噪声的均值为零，即：

S(t)=s(t)+h(t)

(1)

b.用EMD算法分解S(t)，得到各固有模态函数分量，即：

(2)

式中：ci(t)为EMD第一次分解得到的i个固有模态函数分量;r(t)为余项。

c.在S(t)中再次加入高斯白噪声，重复上述步骤(a)、步骤(b)。

(3)

式中：cji(t)为第j次分解出的第i个固有模态函数；rj(t)为第j次的余量。

d.重复步骤k次，会得到k组固有模态分量，将所得结果平均，得到的固有模态是按照高频到低频顺序排列的，即：

(4)

(5)

2 能量曲线

设平均功率为P，采样时间为T，则电能W为

W=P×T

(6)

配电网正常工作时是一个三相对称系统，设ω为角频率，φ为初相，U、I为电压电流的有效值，则整个系统的瞬时功率计算如式(7)，将式(7)带入式(6)中，即可求出信号的能量曲线。

则瞬时功率为

(7)

3 基于EEMD和能量曲线配电网故障选线步骤

当配电系统发生单相接地故障时，各线路将产生不平衡的零序电流，通过零序电流互感器即可获得，则结合EEMD和能量曲线的故障选线步骤如下所示。

a.用EEMD算法对各馈线零序电流进行分解，得到的固有模态函数按照高频到低频顺序排列，因此第一阶固有模态函数暂态含量最为丰富，更能表征故障特征。

b.计算各线路第一固有模态函数的能量曲线，并记录各个曲线的能量峰值。

c.构建信心度函数设为λ，则

(8)

式中:n为故障线路数量；Ij为线路j的零序电流峰值；Wj为线路j的能量最大值。比较各线路信心度大小完成选线。

4 仿真试验

应用ATP-EMTP仿真配电网，其中中性点采用经消弧线圈接地方式，简化模型如图1所示。

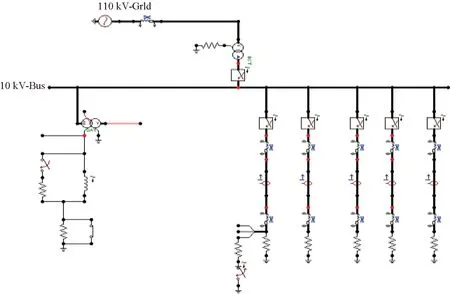
图1 简化配电线路

包含5条线路，各线路参数如下所示:

R1=0.012 73 Ω/km,R0=0.3863 Ω/km,

L1=0.9337 mH/km,L0=4.1264 mH/km,

C1=12.74 nF/km,C0=7.751 nF/km

(9)

假设线路1发生故障，接地电阻为150 Ω，故障角度为π/6，故障点距离母线5 km，则各线路零序电流如图2所示。

图2 各线路零序电流图

采用EEMD算法对各线路零序电流进行分解，所得结果如图3所示。

(a)线路1分解结果

然后通过计算求出每条线路EEMD分解的第一阶固有模态函数能量曲线如图4所示，找到各线路能量峰值分别为0.712 43、0.0838、0.018 07、0.006 21和0.005 26。计算每条线路的选线信心度完成故障选线。表1为构建信心度的各个参量及信息度值，可以看出线路1的信心度最大，即为故障线路。

图4 EEMD分解的各线路第一阶固有模态函数能量曲线

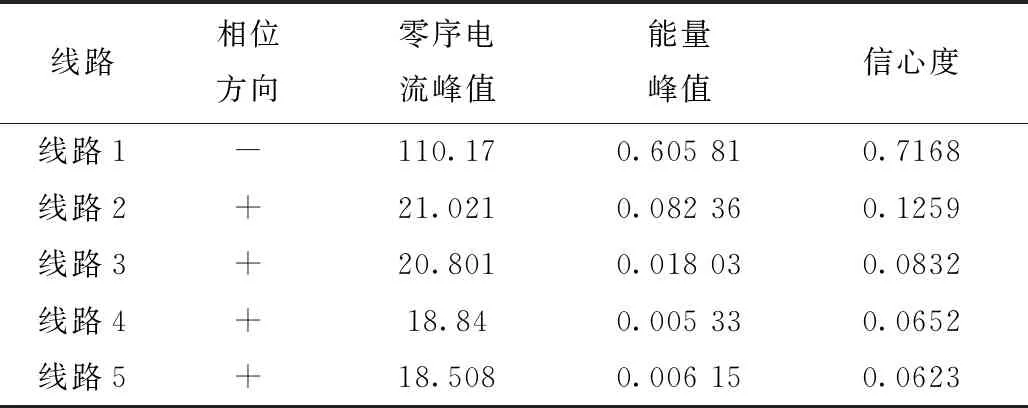
表1 构建信心度的参量及信息度值

5 实际线路故障选线

某市区发生单相接地故障。采样频率为2 MHz，包含了5条电缆线路，线路2发生故障。

图5为故障线路2的零序电流，图6为线路3的零序电流。图7为故障线路2的EEMD分解的第一固有模态函数图，图8为线路3的EEMD分解的第一固有模态函数图

图5 故障线路零序电流

图6 非故障线路3的零序电流

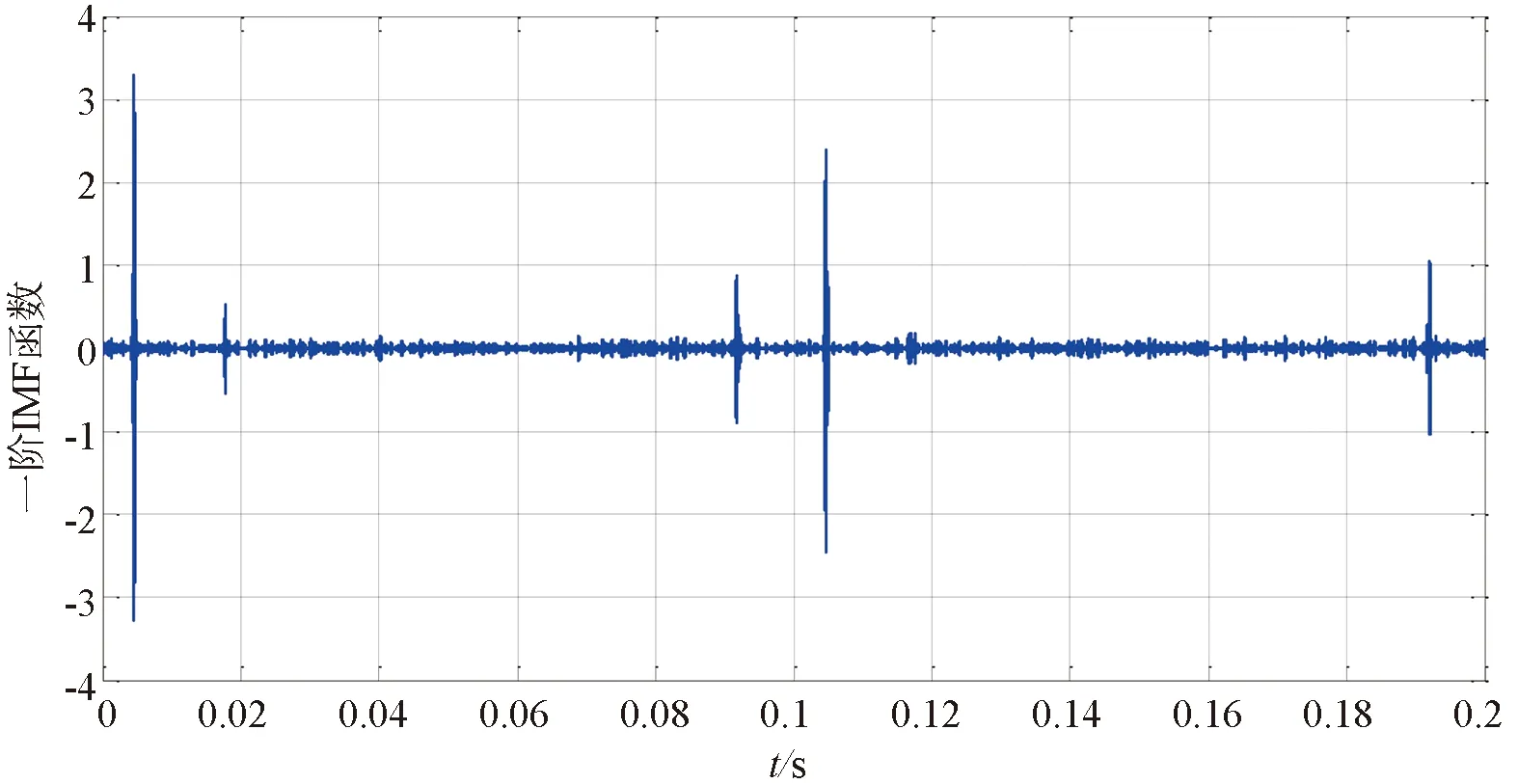
图7 线路2的第一阶固有模态函数

图8 线路3的第一阶固有模态函数

分别计算各线路经过EEMD算法分解后的第一固有模态函数的能量峰值，分别为0.081、0.672、0.032、0.011和0.023。从而得到各线路信息度，分别为0.0322、0.7123、0.065、0.0697和0.0225，可以看出线路2发生故障，与实际情况相符合。综上，本文所提方法能够适用与实际现场的配电网故障保护中。