基于时延扩展的主动测高算法

闫晓峰，张鈺婷，焦 阳，万 群

(1.海军装备部,重庆 405200；2.电子科技大学，四川 成都 611731；3.敏捷智能计算四川省重点实验室，四川 成都 611731)

0 引言

无线电高度计作为飞行平台的必备部件之一，主要为平台的控制系统提供高度信息，是决定飞行安全的重要因素[1-2]。因此，无线电高度计可广泛应用于各飞行场景中，如直升机定高盘旋、飞机起降和海平面高度测量等。随着应用场景的多元化和复杂化，人们对于雷达高度计的性能要求也越来越高，比如其准确性、实时性、稳定性和低截获性等。常见的雷达高度计均采用主动雷达的方式，由飞行平台自身发射信号，到达地面后产生地面回波，由平台自身接收回波信号，并进行分析处理得到平台高度。

根据发射信号的形式，可以将雷达高度计分为3类：调频连续波(FMCW)、准调频连续波(FMICW)和脉冲雷达高度计[3-5]。FMCW高度计的优点有结构简单、发射功率较低、接收机灵敏度较高等，不仅没有距离盲区，还具有较高的距离分辨力。同时，也存在一些固有缺点，比如抗干扰能力差、高空测量难度大且测量精度较低等[6-8]。相对来说，脉冲雷达高度计则具有更高的测高精度，尤其是在高空或超高空上。然而，脉冲雷达高度计峰值功率较高，低截获性较差[9-11]。FMICW高度计是在调频连续波的基础上加波门控制脉冲，在一个时间周期内发射信号，发射机关闭后，接收机开始接收信号，在接收信号的基础上加发射信号互补波门。不仅使收发隔离的问题得到解决，还大大增加了作用距离，降低了平均功率。FMICW高度计兼具FMCW高度计和脉冲雷达高度计的优点，具有绝对的优势[12-15]。

脉冲雷达高度计多采用脉冲前沿跟踪，跟踪点是回波前沿的半功率点，在回波前沿宽度变动的情况下，会造成测高误差[9]。FMICW高度计忽略了多普勒频移的影响，在平台运动速度较大的情况下，测高误差较大。

考虑到波束宽度，回波具有明显的时延扩展。在波束偏角不同时，回波时延扩展信息不同。本文基于主动测高模型，利用时延扩展对波束内侧和外侧的时频信息进行分析，校正波束指向，进而得到准确的高度信息。在波束指向存在偏角时，提高了测高精度。

1 时延扩展测高问题

地面回波信号由反射分量和散射分量构成，反射分量和地面的反射系数有关，散射分量和其散射系数有关，二者都和地面的粗糙程度以及测高雷达的工作频率等相关。其中，回波信号主要取决于散射系数的大小。当信号入射角为0°～40°时，后向散射系数大于0；当入射角大于40°时，后向散射系数为0，即无散射回波。

无线电高度计一般是利用发射部分向地面发射一系列天线波束，通过地面反射形成回波信号，利用回波信号相比于发射信号的延迟即可完成测高。理论上来说，高度h应利用天底点的反射回波时延τ0来计算，即：

(1)

式中，光速c=3×108m/s。当发射波束指向存在一定的偏角时，会导致波束并非垂直照射地面，即波束中心线与地面法线方向不重合。这种情况下并不能直接得到τ0。通过地面回波分析，可以得到最短的回波时延τmin和最长的回波时延τmax，判断波束指向，得到准确的天底点回波时延τ0，进而计算高度h。

在面目标的情况下，地面回波信号可以表示成发射信号关于时延和频移的二重积分，也是存在时延扩展和多普勒频移扩展。本文仅对时延扩展进行研究，因此，将地面分成M个等距离环，有：

(2)

式中，σm为第m个等距离环的散射系数；τm∈[τmin,τmax]为第m个等距离环回波时延，二者均与信号入射角有关。在这里，信号入射角与高度、波束宽度及波束偏角有关。n(t)为零均值，方差为σ2的高斯白噪声。

因此，将时延扩展测高问题转化为时延估计问题，即对回波信号sr(t)进行时域处理，得到最短时延和最长时延，利用二者的关系，判断波束指向，并估计高度。

2 时延扩展测高算法

传统的测高方法是对回波前沿估计，根据其对应的时延测得高度。在波束指向存在偏角的情况，仅由回波前沿测高会带来误差。上一节中，地面回波信号进行了时延估计，可以得到回波的最短时延和最长时延。当波束偏角和半波束宽度的大小关系不同时，最短时延和最长时延的关系也不同。因此，本节将讨论不同波束照射模型下的测高方法。

2.1 波束垂直指向地面

一般来说，当波束中心直接指向天底点时，最短回波时延τmin即和待估计的τ0相等。测量模型如图1所示。

图1 波束垂直发射时的测高模型Fig.1 Altimeter model diagram when the beam is pointed vertically to the ground

图1中，φ=0°为波束偏角，定义为雷达发射波束的中心线与地面法线方向的夹角，θ为半波束宽度，τmin为最短回波时延，τmax为最长回波时延。此时2个回波时延之间满足：

(3)

此时，波束偏角φ=0°，高度可以由最短波时延τmin确定：

(4)

2.2 波束偏角小于半波束角

当波束中心并不直接指向天底点O时，最早到达的波束应为O点的反射回波，最晚到达波束为波束投影面距离天底点最远的散射点Q。定义波束中心线在法线右侧时，波束偏角大于0°，波束中心线在法线左侧时，波束偏角小于0°。模型如图2和图3所示。

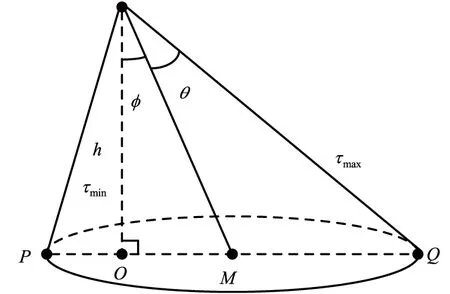
图2 波束偏角0°<φ<θ时的测高模型Fig.2 Altimeter model diagram when 0°<φ<θ

图3 波束偏角-θ<φ<0°时的测高模型Fig.3 Altimeter model diagram when -θ<φ<0°

图2和图3中，θ为半波束宽度，φ为波束中心线偏离地面法线方向的角度。当|φ|<θ时，最短回波时延为τmin，最长回波时延为τmax，此时，时延之间的关系为：

(5)

当θ∈[0,90°)，|φ|<θ时，显然(θ+|φ|)∈[0,180°)，cos(θ+|φ|)单调递减，因此，cos(θ+|φ|)∈(cos 2θ,cosθ)。此时，波束偏角和高度可以由最短回波时延τmin和最长回波时延τmax确定：

(6)

(7)

Q点的入射角最大，要想让整个地面照射圆的信号都能返回平台，则

θ+φ≤40°，

(8)

此时，波束偏角测量满足式(6)。

2.3 波束偏角大于半波束角

波束以角度φ照射到地面，当|φ|>θ时，最早的回波距离大于真实高度，需要根据实际测出的最短回波时延τmin和波束偏角，来估计雷达高度。模型如图4和图5所示。

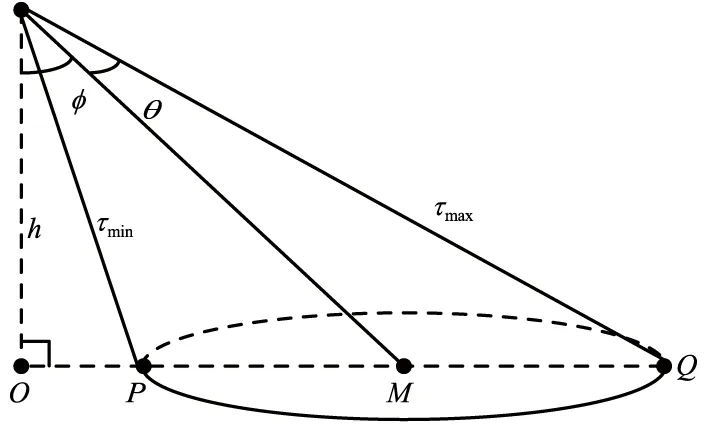
图4 波束偏角φ>θ时的测高模型Fig.4 Altimeter model diagram when φ>θ

图5 波束偏角φ<-θ时的测高模型Fig.5 Altimeter model diagram when φ<-θ

当|φ|>θ时，最早的回波距离也比真实高度要大，且二者之间的夹角为|φ|-θ。最短回波时延为τmin，最长回波时延为τmax，由几何关系有，最短时延和最长时延的比值为：

(9)

当入射角大于40°时，无后向散射回波。也就是说要收到回波，且|φ|∈(θ,90°)，波束偏角应满足:

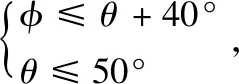
(10)

由式(9)还可以推得|φ|的计算式：

(11)

此时，高度和最短回波时延之间的关系为：

(12)

因此，在波束指向不同时，可以根据最短回波时延和最长回波时延来确定波束偏角，并准确测量高度。

3 仿真实验

假设发射机发射脉冲信号，脉内为线性调频信号，脉宽为T=5 μs，调频带宽为B=30 MHz，采样率为fs=60 MHz。在飞行平台与天底点的高度为H=9 km，发射信号半波束宽度角为θ=30°的情况下，分别对波束偏角φ为0°,15°,45°情况进行仿真实验。

考虑森林地形，入射角为0°～40°的情况下，散射系数为0.9～0.3。仅考虑高斯白噪声的干扰时，半波束角θ=30°，波束垂直指向地面的情况下，通过回波分析来估计最短时延和最长时延。

在本节采用一种基于乘积指数滤波器的方法来估计时延。将回波信号输入乘积指数滤波器，对其输出响应的幅值进行极大值搜索，即可得到多个等距离环对应的时延估计值。回波信噪比SNR=0 dB时，利用乘积指数滤波估计时延的示意图如图6所示。

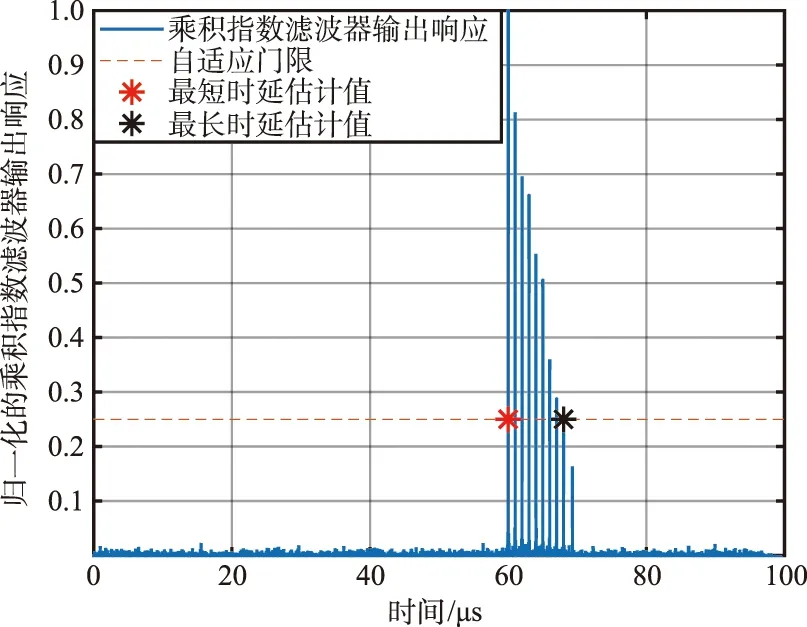
图6 SNR=0 dB时，时延估计示意Fig.6 Schematic diagram of time delay estimation when SNR=0 dB

由图6可以看出，每一个等距离环都对应一个输出响应的峰值，合理设置自适应门限，即可得到每一个等距离环对应的时延。

信噪比变化时，最短时延和最长时延估计的均方根误差图如图7所示。

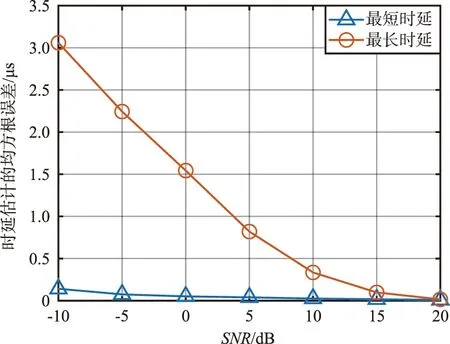
图7 信噪比变化时，时延估计均方根误差图Fig.7 RMSE of time delay estimation when SNR changes

由图7可以看出，最短时延估计误差较小，最长时延估计误差较大，这是因为最短回波时延对应的回波功率较强，而最长回波时延对应的回波功率较弱，容易被噪声掩盖。信噪比不断增加时，2个时延估计的均方根误差均减小，当SNR=20 dB时，最短回波时延估计均方根误差为10 ns，最长回波时延估计均方根误差为16 ns。

波束偏角φ为0°,15°,45°时，波束偏角估计均方根误差图如图8所示。

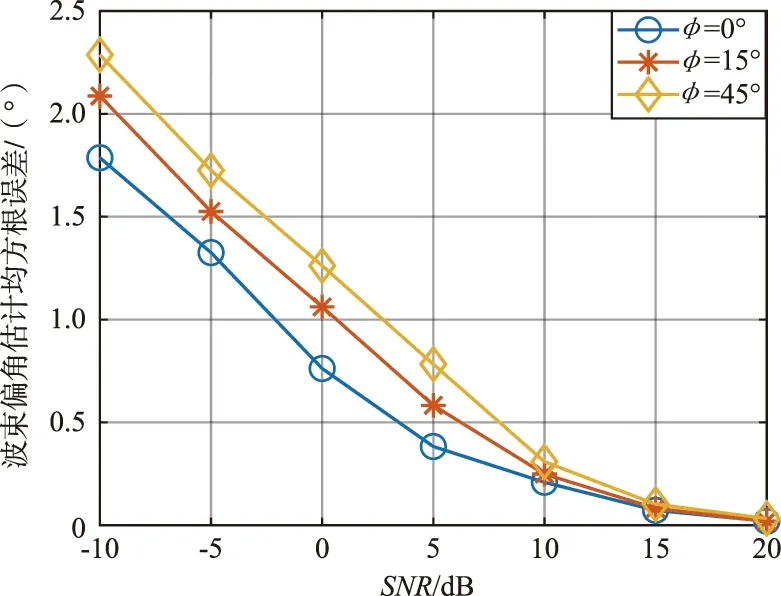
图8 波束偏角φ为0°,15°,45°时，偏角估计均方根误差图Fig.8 RMSE of beam deviation angle estimation when φ=0°,15°,45°

由图8可以看出，随着信噪比增加，波束偏角估计误差减小。波束偏角越大，偏角估计误差越大，这是由于波束偏角越大，回波功率越小，时延估计误差越大。

波束偏角φ为0°,15°,45°时，高度估计相对误差图如图9所示。

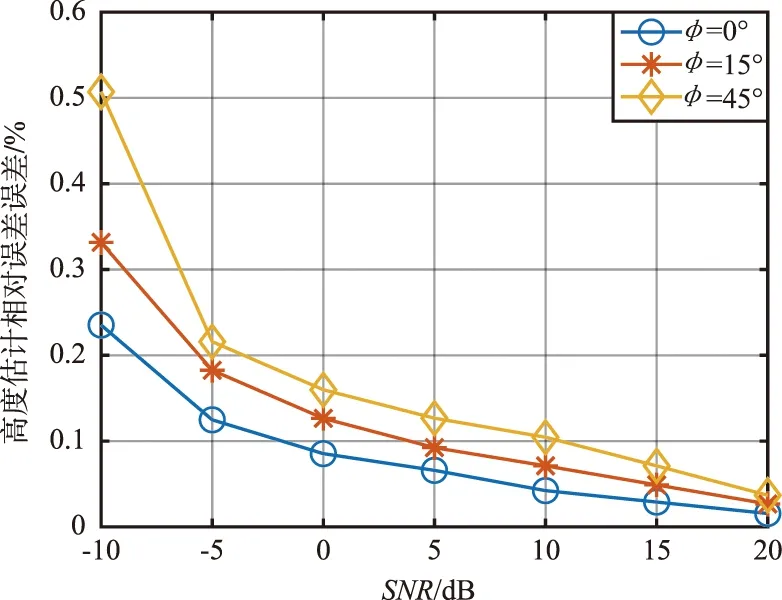
图9 波束偏角φ为0°,15°,45°时，高度估计相对误差图Fig.9 Relative error of height estimation when φ=0°,15°,45°

由图9可以看出，高度估计误差受时延估计误差的影响，波束偏角增大，测高误差增大。

4 结束语

考虑波束指向存在偏角的情况，通过对大地回波信号的分析，将地面目标进行离散化。借助这一模型，提出了一种时延扩展的测高方法。传统的测回波前沿的方法不仅存在波束偏角的问题，还存在回波前沿很难判定的问题，使得测高的精度急剧下降。时延扩展的测高方法不仅可以准确判断波束指向，还可以校正波束偏角带来的测高误差，具有较高的精确性和鲁棒性。首先在波束存在偏角的情况下，分别针对波束偏角为0°、小于半波束角、大于半波束角的情况，得到了波束偏角估计和高度估计的结果。通过仿真验证，证明了该方法的可行性和有效性。