一种参差动目标显示滤波器优化设计方法
2021-08-11刘卫平陈业伟赵晨帆徐安琪
刘卫平,陈业伟,赵晨帆,徐安琪,方 明
(上海航天电子通讯设备研究所,上海 201109)
0 引言
雷达检测的目标一般存在于各种复杂的杂波环境中,如地物杂波、云雨以及人为释放的箔条等,且运动目标的回波电平往往比杂波电平低很多倍,运动目标回波被“淹没”在杂波中,为了检测运动目标,必须对杂波进行抑制[1]。动目标显示(Moving Target Indication,MTI)技术是目前抑制杂波技术中最常用和易于实现的方法,其基本原理是:基于回波多普勒信息的提取而区分运动目标与固定目标[2](包括低速运动的杂波等)。
一般MTI滤波器的频率特性都是以一个脉冲周期响应为准,在频率上周期重复出现单一的脉冲重复周期会使得滤波器产生盲速效应[2]。采用脉冲重复频率(Pulse Repetition Frequency,PRF)参差技术(改变脉冲间的脉冲重复周期),可将盲速扩展[3-4],覆盖目标的最大可能速度响应,通过优化PRF参差比可以进一步优化MTI滤波器性能。
在最大参差比给定的情况下,使第一零点深度最浅的参差比称为最优参差比。PRF参差比的搜索方法有很多种,如枚举法、遗传算法[5-6]等,但枚举法搜索效率较低,遗传算法收敛速度较慢,2种方法都存在搜索时间长的问题。对最优参差码的选择,工程中有时会采用经验值设计法,如采用俄式摆动规律计算参差码,可根据公式快速计算出一组参差码,节约优化时间,但俄式摆动法参差比并非最优,杂波对消效果达不到预期,或者是对运动目标损耗较大,导致雷达无法检测到运动目标,无法满足工程需求。
本文基于某型号相控阵雷达设计提出了一种改进的参差MTI滤波器设计方法。该方法将枚举法与俄式摆动法相结合,既避免了枚举法的盲目搜索,又能够在工程应用中快速达到最优参差比,提高了算法效率,优化了算法性能。
1 MTI滤波器及杂波模型设计
滑窗参差MTI滤波器模型如图1所示[7-8],设计的MTI滤波器采用二阶横向FIR滤波器[9-11]结构,并经过滑窗处理。假设在一个波束驻留时间内雷达有效脉冲数为5个,分别定义发射脉冲周期为T1,T2,T3,T4,T5,通常最后一个脉冲在参与对消运算中,不影响MTI的综合幅频响应,第一个脉冲和最后一个脉冲取系统所允许的最短脉冲,即满足雷达要求的最短量程即可,有T1=T5。在大多数的应用场合下,以4周期的参差比最好,因此,采用4脉冲参差:

图1 滑窗参差MTI滤波器模型Fig.1 Sliding window staggered MTI filter model
T1:T2:T3:T4:T5=K1:K2:K3:K4:K1。
模型中包含的杂波模型为地物杂波[12-14],其固定地物的多普勒频率为零,但由于地物植被等在风力作用下摇摆,使得其杂波呈现一种高斯杂谱,其功率谱表达式为[15]:
(1)
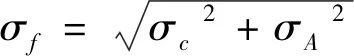
σc=2σv/λ,
(2)
σA=0.265fr/k。
(3)
式(2)中,σv为杂波谱径向速度的标准偏差;σc为杂波功率谱的标准偏差;λ为雷达工作波长。式(3)中,σA为天线扫描引起的杂波谱展宽;fr为平均脉冲重复频率k为天线水平波束宽度内的脉冲数。
2 最优参差码搜索方法对比
2.1 枚举法
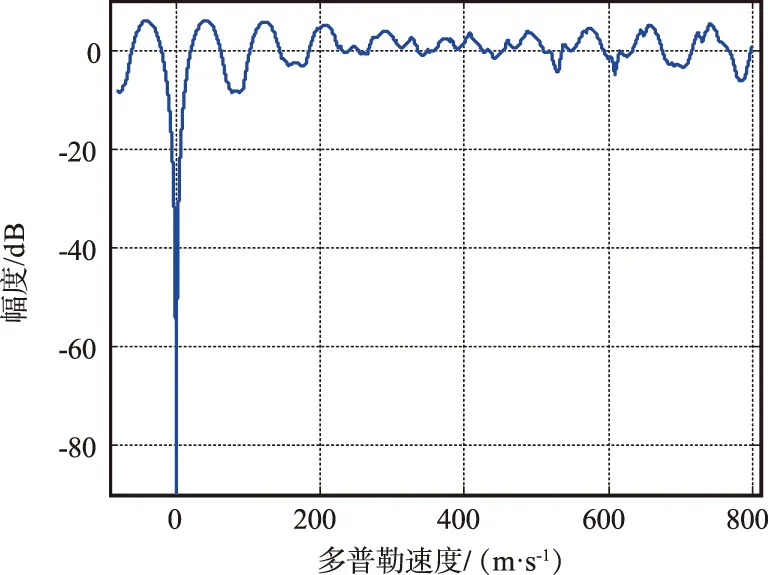
枚举法:假设4脉冲参差比为K1:K2:K3:K4,且有K1 (4) (5) 式中,Kmin和Kmax分别为最小参差码和最大参差码;r为最大参差比,在式(4)、式(5)中,满足r=K4/K1,r通常由系统允许的休止期决定;Kav为搜索区间的参差码,通过解该方程组可得Kav值的取值范围。 在r<1.2,K1最小取值为307,N=4的情况下,有: 若通常参差码Kav取整,选择范围为323≤Kav≤353,K1为最小参差码,不能大于Kav的下限,则K1取值范围为: 307≤K1≤323。 K4为最大参差码,不能小于Kav的上限,上限为K1乘以最大参差比r,即323×1.2,则K4取值范围为: 353≤K4≤387, 则Kav都不能超出K1,K4的搜索区间,有: 307≤Kav≤387。 俄式摆动法是采用设定的参差码的方法,使发射脉冲重复周期满足以下摆动规律: T1T1+2ΔTT1+1/2ΔTT1+3ΔTT1+1/3ΔT+…+T1。 (6) 通过对T1,ΔT的合理选择,可以得到一组参差码。这种选择方法基于工程设计经验,可以快速得到一组参差重复周期,算法效率较高,缺点是不一定是最优解。 本文提出了一种基于枚举法与俄式摆动法相结合的算法。通常,在允许的门限范围内,MTI滤波器基本符合最大参差比越大,第一零点深度越浅的规律。在该示例中,由俄式摆动法可知最大参差比: r=T4/T1。 (7) 因此,通过设定最大参差比r的值,可以首先确定T1和T4,通过俄式摆动法求得ΔT,继而可确定T2,T3。这样,可以得到一组初始脉冲重复周期。 设定最大参差比r范围,可以得到几组初始重复周期。同时,还可以增加雷达系统限定的约束条件,所有的脉冲重复周期之和不能超过一帧驻留时间,如超过帧驻留时间,可以将该组脉冲重复周期剔除。 为了进一步减少搜索量,对得到几组初始重复周期求相应MTI滤波器综合幅频响应,在目标可能出现的最大速度范围内,若等效第一盲速以外凹口深度要比等效第一盲速凹口深,则舍去该组初始重复周期。 其次,对比筛选剩下的几组脉冲重复周期的综合幅频响应的通带内平坦度,选取通带平坦度较好的,可给定一个约束值,在约束值范围内的都可保留。通带平坦度为频率响应超过零之后的均方根: (8) 式中,σs为通带平坦度;xi为通带范围内幅频响应曲线的幅度值。 然后基于优化准则在小范围内对一组重复周期的T2,T3进行微调。定义的优化准则为: ① 综合幅频响应曲线等效第一盲速凹口的深度大于指定值; ② 通带内平坦度小于指定值。 选取的最优参差比可最优先满足条件①,其次是条件②,最后将条件①和条件②相减最大值作为最终约束条件。 改进的优化搜索流程如图2所示。 图2 优化搜索流程Fig.2 Search process optimization 设定仿真条件为:T1=307,最大参差比1.19 在仿真条件下,使用2.1节枚举法进行运算,可以得到: 307≤Kav≤383。 该区间有77个数,可从中任取出4个组合,得到符合条件的参差码排列组合数量为676 640组。分别用这些参差码求相应MTI滤波器综合幅频响应,再对比等效第一盲速凹口、带内平坦度等指标,耗费的时间最长,算法效率最低。 在仿真条件下,使用2.2节俄式摆动法进行运算,有效条件为T1=307。依据工程经验,令ΔT=T1/15,取整后得到1组固定的参差码:307,347,317,368,313。得到的MTI滤波器的综合幅频响应如图3所示。 图3 俄式摆动法得到的MTI滤波器综合幅频响应Fig.3 The comprehensive amplitude-frequency response of the MTI filter obtained by the Russian wobble method 这种方法得到参差比的效率最高,但同时也无法验证这种方法得到的滤波器幅频响应是否为最优解。 在仿真条件下,使用2.3节改进的优化搜索法进行运算,可以得到36组初始重复周期。通过对参差比的优化,得到一组改进的参差MTI滤波器,该滤波器的综合幅频响应如图4所示。由图可见该组滤波器具有较浅的第一零深和比较好的通带平坦度,基本可满足MTI滤波器设计要求。 图4 几组不同参差比的MTI综合幅频响应Fig.4 MTI comprehensive amplitude-frequency responses of several sets of different stagger-code ratios 在该组重复周期中选取一组第一零深最浅,且通带平坦度最好的一组曲线,其综合幅频响应曲线如图5所示。 图5 优化后的MTI滤波器综合幅频响应Fig.5 Comprehensive amplitude-frequency response of the optimized MTI filter 由图5可以看出,该方法的算法效率比俄式摆动法低,但较枚举法更高;对比算法效果(图3和图5)可以看出,该方法的等效第一盲速凹口的深度更浅,且通带内更为平坦。 采用该滤波器参差比优化搜索方法设计的MTI用于某相控阵雷达,图6为MTI对消前的雷达显界面,图7为MTI对消后的雷达显界面。 图6 MTI对消前雷达显示界面Fig.6 Radar display interface before MTI cancellation 图7 MTI对消后雷达显示界面Fig.7 Radar display interface after MTI cancellation 由图可见,采用该设计方法设计的MTI滤波器可有效抑制地物杂波,该参差比优化设计方法有效可行。 本文介绍的5脉冲4参差的设计优化结果,对于脉冲数较多,参差数大于4的重频周期,也同样可行。 本文详细介绍了一种改进的参差MTI滤波器设计方法,设计将传统的枚举法与工程中采用的俄式摆动法相结合,得到初始的脉冲参差比,将等效第一盲速凹口深度和滤波器通带平坦度作为择优条件,搜索到优化的参差比,从而达到优化设计MTI滤波器的目的。该方法的算法效率优于枚举法,节省了数十万的试错机会,算法性能优于俄式摆动法。对比仿真结果发现,得到的MTI滤波器综合幅频响应等效第一盲速凹口的深度更浅,且通带内更为平坦,具有更好的滤波器特性。该MTI滤波器参差比优化搜索方法已成功应用于某相控阵雷达,设计方法也可以作为其他MTI滤波器设计的参考。
2.2 俄式摆动法
2.3 改进的优化搜索法


3 仿真与测试




4 结束语
