基于伸缩步长法的高坝大库放空时间计算研究

李大成，蒲小芳，宋 雄，黄文波，吴 迪

(中国电建集团贵阳勘测设计研究院有限公司，贵州 贵阳 550081)

1 研究背景

随着经济社会发展的需要，我国在水资源开发条件好、地形地质条件合适地区建设有许多高坝大库。高坝大库在实现水资源调控、合理配置水资源及缓解日益加剧的水资源供需矛盾等方面发挥着重要作用，是促进经济社会又好又快发展的重要工程措施[1]。高坝大库也存在安全风险，加强高坝大库运行安全风险分析工作，提高对其安全风险预防和控制能力，确保高坝大库建设及运行安全，是关系到人民生命财产安全和国家经济社会可持续发展的热点问题[2]。我国高坝大库工程建设和运行经验表明，设置放空设施可有效降低库水位，在降低工程事故发生率、减轻事故灾害影响、提高工程安全运行保障等方面效益显著，可避免重大灾难性事故的发生，为工程检修、重大灾难应急抢险提供最直接有效的支持[3-7]。放空时间是从启动放空时的库水位降至放空过程中所能达到的最低库水位的时间，是高坝大库放空设施设计、应对工程检修和应急抢险科学决策的重要参数。

目前，水库放空相关研究主要集中在放空建筑物优化设计[8-9]、放空数值模拟[10-11]、多通道协同放空[12]、深度放空[7]等方面。张丹等[8]针对下坝水库地形地貌、地质条件较复杂、岩体较破碎易形成滑坡、崩塌、偏压、泥石流等问题，优选“利用导流隧洞改为有压取水/放空隧洞”的“一洞三用”取放水方案。王春柳[9]通过多方案优化设计与分析，解决了狮溪水库取水洞、放空洞及导流洞“三洞合一”的布置方案在施工过程中相互影响的难题。李昂[10-11]利用RNGk-ε紊流模型和标准壁面函数模拟非恒定紊流，利用VOF模型追踪水流自由界面，通过数值模拟计算得到了精度较高的放空全时域过程。李远程等[12]结合工程实例论证了各种泄水建筑物的协同放空流程，说明了增加低位泄水建筑物的必要性和改进放空建筑物布置以提高放空能力的可行性。杨家修等[7]针对高坝枢纽放空系统存在放空深度有限、放空速度慢、放空时段单一及放空能力不满足应对突发险情要求的技术难题，基于反向水推力和分层流道接力泄水的原理，提出了连续多级闸门联合挡水的新型放空系统解决方案。

然而，放空时间计算相关的研究较少。宋萌勃[13]通过实例说明了放空时间计算的解析法，建立了一种有利于水库控制运用的多轴相关图。叶伟红[14]在分析计算水库放空时间的微积分法、图解法、调洪演算置零法的基础上，提出了以库水位下降、库容减少为特征的计算机程序方法。马淑君等[15]以天生桥一级水电站为实例，详细介绍了水库放空时间计算的数解法和图解法。由于水库水位-面积-库容方程、水库水位-泄流流量方程概化难度大，放空系统可能由多个泄流设施组成，难以通过微积分法、解析法计算放空时间。图解法虽直观易掌握，但存在作图工作量大、耗时多、精度有限等局限性。

高坝大库放空系统一般由多层放空设施组成，闸门启闭受作用水头限制，泄流曲线常呈现突变现象(水库水位降低至某一水位，泄流能力突然加大或减小)，难以采用常规的微积分法、解析法、图解法及数值解法计算放空时间。针对此问题，本文提出以泄流曲线突变水位为控制，将泄流曲线分段，各分段泄流曲线采用伸缩步长法离散，基于离散水位区间水量平衡推算高坝大库放空时间的方法，通过某案例工程放空时间计算验证该方法的可行性及合理性，可为国内外高坝大库放空时间计算提供经验借鉴和参考。

2 研究方法

2.1 基本原理

水库放空时，由于放空设施作用水头随时间变化，下泄流量亦随之变化，即为非稳定流。根据水流连续方程，在dt时间内水库来泄水量(dV=Qdt)，等于水库水位下降而减少的库容dV，即

dV=Qdt=-Adz

(1)

式中，A为水库库面面积；Q为与水库水位(面积)相对应的扣除来水后的下泄量。

水库放空时间为

(2)

采用微积分法计算水库放空时间时，需建立水库水位-库面面积-下泄流量曲线方程，而这些方程往往是分段非线性的，致使微分方程变得很复杂，难以积分求解。在实际计算中，通常采用数值解法计算水库放空时间。

在某一时段t内，水库的水量平衡方程式为

(3)

水库水位-面积-库容曲线一般根据实测地形图量算得到，采用一系列离散点据表示，通常假定相邻离散点之间的水库面积、库容是线性变化的，各水库水位对应水库面积、库容可通过线性插值得到。水库放空设施的泄流能力一般根据放空建筑物尺寸按经验公式计算得到，为连续曲线，采用数值解法计算水库放空时间时需对水库水位-泄流流量曲线进行合理离散。

2.2 水库水位-泄流流量曲线离散

水库放空系统通常由溢洪道、泄洪洞、放空洞等多个泄流设施组成，水库水位-泄流流量曲线为分段连续曲线，数学模型为

(4)

式中，qz为水库水位Z对应的泄流流量；f1(Z)、…、fn(Z)为各放空设施泄流能力数学公式；Qe为机组发电流量；Znormal、Zdead分别为水库正常蓄水位、死水位；Zpoint1、…、Zpointn分别为水库水位-泄流流量曲线突变点对应水位。

水库水位-泄流流量曲线通常采用水位等间距离散方法(如等间距为2、1、0.5 m等)，等间距的选取存在一定的随意性，难以保证相邻离散点之间的泄流流量可采用线性概化，导致水库放空时间计算成果精度难以控制，如何科学合理离散水库水位-泄流流量曲线是计算水库放空时间的关键。

为合理离散水库水位-泄流流量曲线，本文引入伸缩步长法[16]，伸缩步长法具有数学模型简单、可等误差控制、离散点据适中等优点。基本原理为设水库泄流设施泄流能力方程为q=f(Z)，建立如图1所示的曲线。

图1 伸缩步长法离散泄流系统泄流能力曲线原理

以点A(ZA，qA)为起点，水位初步步长取为z，z值一般取允许误差δ的5～10倍，沿Z的方向以z值前进一步，到达点B(ZB，qB)，即ZB=ZA+z、qB=f(ZB)；连接点A、点B，计算AB直线段与曲线q=f(Z)的最大间距δα；若δα≥δ，则需缩短步长z，重新计算AB直线段与曲线q=f(Z)的最大间距δα，直到最大误差值δα小于允许误差值δ。

为简化AB直线段与曲线q=f(Z)的最大误差值δα的数学模型，以及便于计算程序编制，沿Z轴方向按等分形式将步长z分为若干等分点，计算出与各等分点对应的AB直线段与曲线q=f(Z)的误差值，并从中找出最大的误差值，即为AB直线段与曲线q=f(Z)的最大误差值δα。

假设点Z为水位初步步长z上的一个等分点(见图1)，点Z对应的AB直线段与曲线q=f(Z)的误差值为ED。过点Z作Z轴的垂线与曲线q=f(Z)和AB直线段分别相交于点D和点C，再过点D作AB直线段的垂线，交于点E，则

(5)

(6)

CD=k(ZT-zA)+qA-f(ZT)

(7)

2.3 放空时间计算流程

高坝大库放空出库流量需考虑各放空设施泄流能力和机组发电流量，受闸门启闭作用水头限制和机组发电水位要求，泄流曲线常呈现突变现象。若以计算时段为控制推求时段末水库水位时，难以合理处理泄流曲线突变情况；需以泄流曲线突变水位和放空平衡水位(水库放空接近底部时，入库流量与出库流量相等时对应的水位)为控制点，将泄流曲线分为多段曲线，各段泄流曲线采用伸缩步长法进行离散，并计算各相邻离散水位的放空时间，统计水库从启放水位下降至放空平衡水位所需要的时间，即为水库放空时间，计算流程如图2所示。

图2 基于伸缩步长法的高坝大库放空时间计算流程

基于伸缩步长法的高坝大库放空时间计算公式为

(8)

(9)

3 实例研究

3.1 工程概况

某工程正常蓄水位2 895.0 m，死水位2 815.0 m，调节库容24.33亿m3，属年调节水库，为一等大(1)型工程。工程放空系统由溢洪道、泄洪洞、第一层放空洞、第二层放空洞及引水发电等多个设施组成。溢洪道为洞式溢洪道，设置3个开敞式孔口，孔口尺寸为15 m×22 m(宽×高)，堰顶高程2 873.0 m。泄洪洞采用无压洞型式，进水塔底板高程为2 827.0 m，顶高程2 907.0 m，工作闸门为1孔，孔口尺寸为7 m×13 m(孔-宽×高)。第一层放空洞进水塔底板高程为2 786.0 m，设置一扇检修闸门和一扇工作闸门，孔口尺寸均为7 m×15.5 m，闸门最大工作水头72.0 m(即最大工作水位2 856.0 m)。第二层放空洞进水塔底板高程为2 745.0 m，设一扇检修门和一扇工作门，孔口尺寸均为7 m×15.5 m，闸门最大工作水头72.0 m(即最大工作水位2 817.0 m)。引尾水系统布置于右岸，由塔式进水口、引水隧洞、压力钢管、尾水隧洞、尾水调压室及尾水闸室等建筑物组成，机组满发流量为1 201 m3/s。

3.2 放空设施开启顺序

工程放空设施开启顺序为：

(1)水库水位在溢洪道堰顶高程2 873.0 m以上时，放空系统为溢洪道+泄洪洞+引水发电系统。

(2)水库水位在第一层放空洞最大工作水位2 856.0 m与溢洪道堰顶高程2 873.0 m之间时，放空系统为泄洪洞+引水发电系统。

(3)水库水位在泄洪洞底板高程2 827.0 m与第一层放空洞最大工作水位2 856.0 m之间时，放空系统为泄洪洞+第一层放空洞+引水发电系统。

(4)水库水位在第二层放空洞最大工作水位2 817.0 m与泄洪洞底板高程2 827.0 m之间时，放空系统为第一层放空洞+引水发电系统。

(5)水库水位在死水位2 815.0 m与第二层放空洞最大工作水位2 817.0 m之间时，放空系统为第一层放空洞+第二层放空洞+引水发电系统。

(6)水库水位在第一层放空洞底板高程2 786.0 m与死水位2 815.0 m之间时，放空系统为第一层放空洞+第二层放空洞。

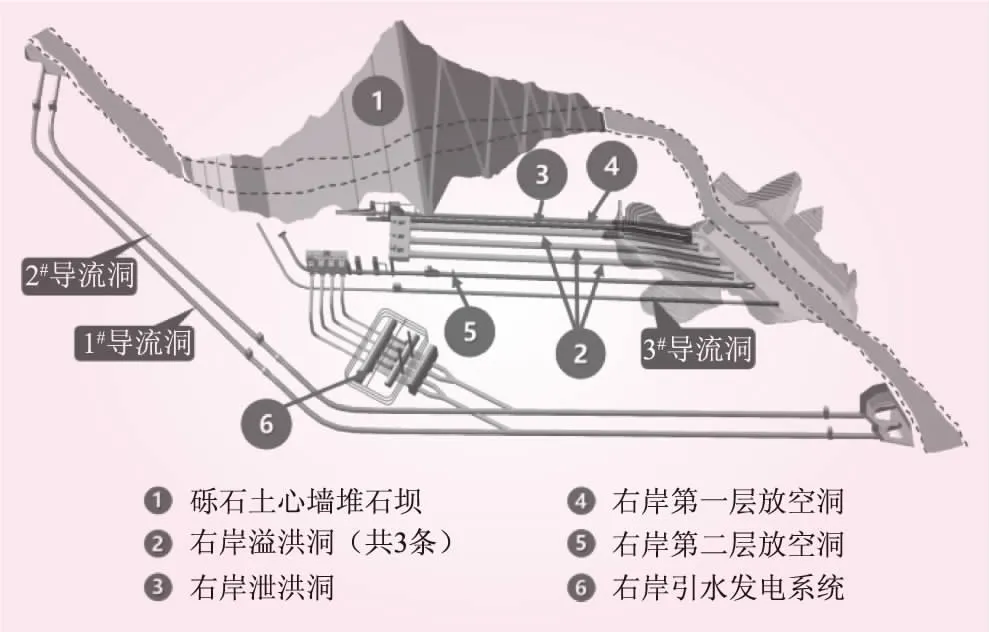
图3 某工程枢纽平面布置示意

(7)水库水位在第二层放空洞底板高程2 745.0 m与第一层放空洞底板高程2 786.0 m之间时，放空系统为第一层放空洞。

3.3 放空时间计算

3.3.1 基本资料

工程坝址径流、洪水成果见表1、表2，工程库容曲线、泄流曲线如图4、图5所示。

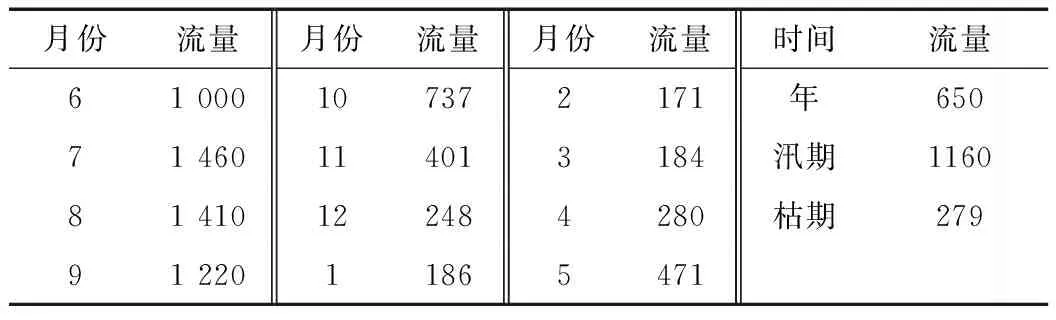
表1 工程坝址多年平均径流成果 m3/s

表2 工程坝址设计洪水成果

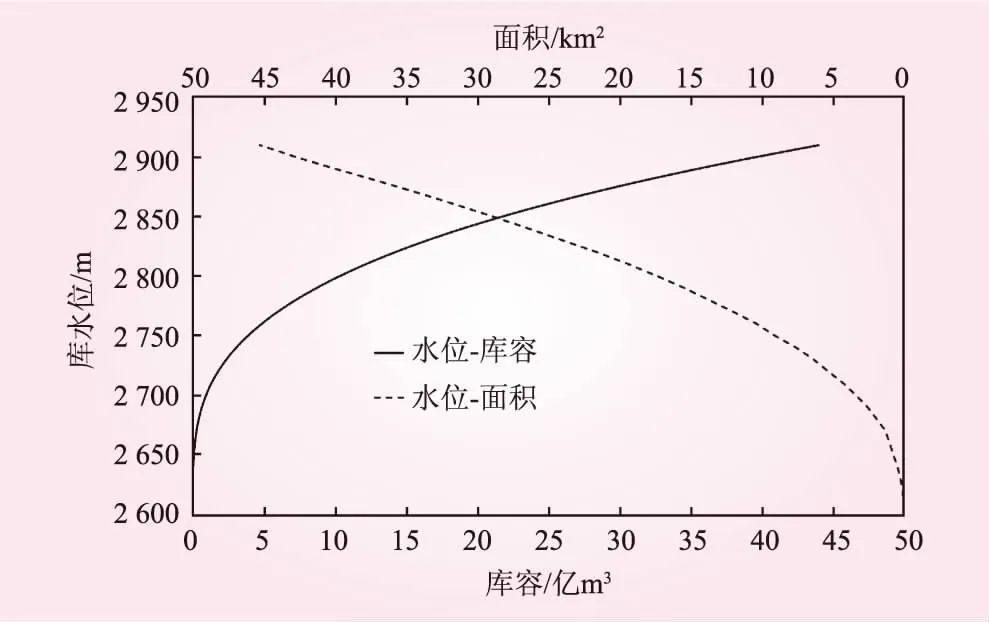
图4 工程水库水位-面积-库容曲线

图5 工程放空系统泄流曲线

3.3.2 计算工况

以应急放空工况为例，分别采用常规方法与伸缩步长法计算工程放空时间。放空计算边界条件为①入库流量按汛期和非汛期多年平均流量考虑；②出库流量考虑机组全部过流，鉴于工程下游河段有集镇，按20年一遇洪水标准控制下泄流量；③启放水位为正常蓄水位。

表3 常规方法和伸缩步长法计算的工程放空时间成果对比

3.3.3 计算结果

根据前述基本资料和方法，采用常规方法和伸缩步长法计算的工程放空时间成果见表3、图6和图7。

图6 常规方法和伸缩步长法计算的放空过程图(汛期)

图7 常规方法和伸缩步长法计算的放空过程图(枯期)

根据表3的计算结果可知，工程库水位从正常蓄水位下降至死水位，伸缩步长法计算的放空时间比常规方法短8.53%～9.79%；库水位从正常蓄水位下降至平衡水位，伸缩步长法计算的放空时间较常规方法短11.6%～11.93%。主要原因为常规方法根据已知时段初水位和入库流量，通过时段水量平衡试算时段平均下泄流量推求时段末水位，时段末水位存在跨越突变水位情况，导致该时段平均下泄流量难以真实反映时段初、末水位之间的泄流曲线变化情况，而伸缩步长法根据泄流曲线变化情况，合理调整泄流曲线离散步长，可较为真实反映泄流曲线。因此，采用伸缩步长法计算多层放空设施的高坝大库放空时间是可行的且精度可靠，可为高坝大库放空设施设计、应对工程检修和应急抢险科学决策的提供合理参数。

4 结 论

本文分析了目前高坝大库放空时间计算存在的问题，针对常规方法难以合理解决泄流曲线存在突变情况的高坝大库的放空时间计算问题，提出以泄流曲线突变水位为控制，将泄流曲线分段，采用伸缩步长法离散各分段泄流曲线，基于离散水位区间水量平衡推算高坝大库放空时间的方法。伸缩步长法具有数学模型简单、误差可控、离散点据适中等优点，离散后的各直线段可较好地代表高坝大库多层放空设施的泄流曲线。以某工程应急工况放空时间计算为例，验证了采用伸缩步长法计算高坝大库放空时间的可行性、合理性及可靠性，可为工程放空设施设计、应对工程检修和应急抢险科学决策的提供合理参数，亦可为国内外高坝大库放空时间计算提供经验借鉴和参考。