采用凸轮驱动的QFP电路分离模具
2021-08-10李庆生汪宗华汪宗宝
李庆生,汪宗华,汪宗宝
(1.铜陵文一三佳科技股份有限公司,安徽 铜陵244000;2.安徽荻港海螺水泥股份有限公司,安徽 芜湖241200)
在使用引线框架封装的电路中,QFP类产品采用四边管脚的封装方式。基于QFP产品的这种特点,它只能采用吸盘吸住产品的方式从引线框架上分离,用装盘的方式来收料(Tray off)。其所使用的分离模具虽然需承载的负荷不高(2 000~3 000 N),但要求稳定可靠,在一个冲切周期内完成检测、定位分离、保持、复位等动作。为此,模具不但需要上下模都能动作,而且相互之间的运动关系必须满足时序要求。一般考虑的是用两套伺服电机来驱动,通过PLC协调上下模之间的运动来实现。考虑到模具的负荷不高,通过一套伺服电机驱动一对凸轮的方式来实现上下模的时序关系,虽然设计上凸轮机构更复杂一些,但整个机构能做到更紧凑,成本更低,也更加稳定可靠。
1 模具结构
模具的整体结构如图1所示,整幅模具分为上下模两部分,采用下置式驱动。模具安装到装置上时,装置上的“顶出块连接钩”(件17)和“拉杆连接钩”(件18)分别扣住模具上的“顶出块”(件14)和“拉杆”(件15)。生产过程中,“顶出块连接钩”先行动作,由“顶出块”推动下模向上运动,完成检测定位动作。此时,上模由“拉杆”带动,向下运动到产品的分离位置,然后由下模再次向上运动完成产品的分离[1]。
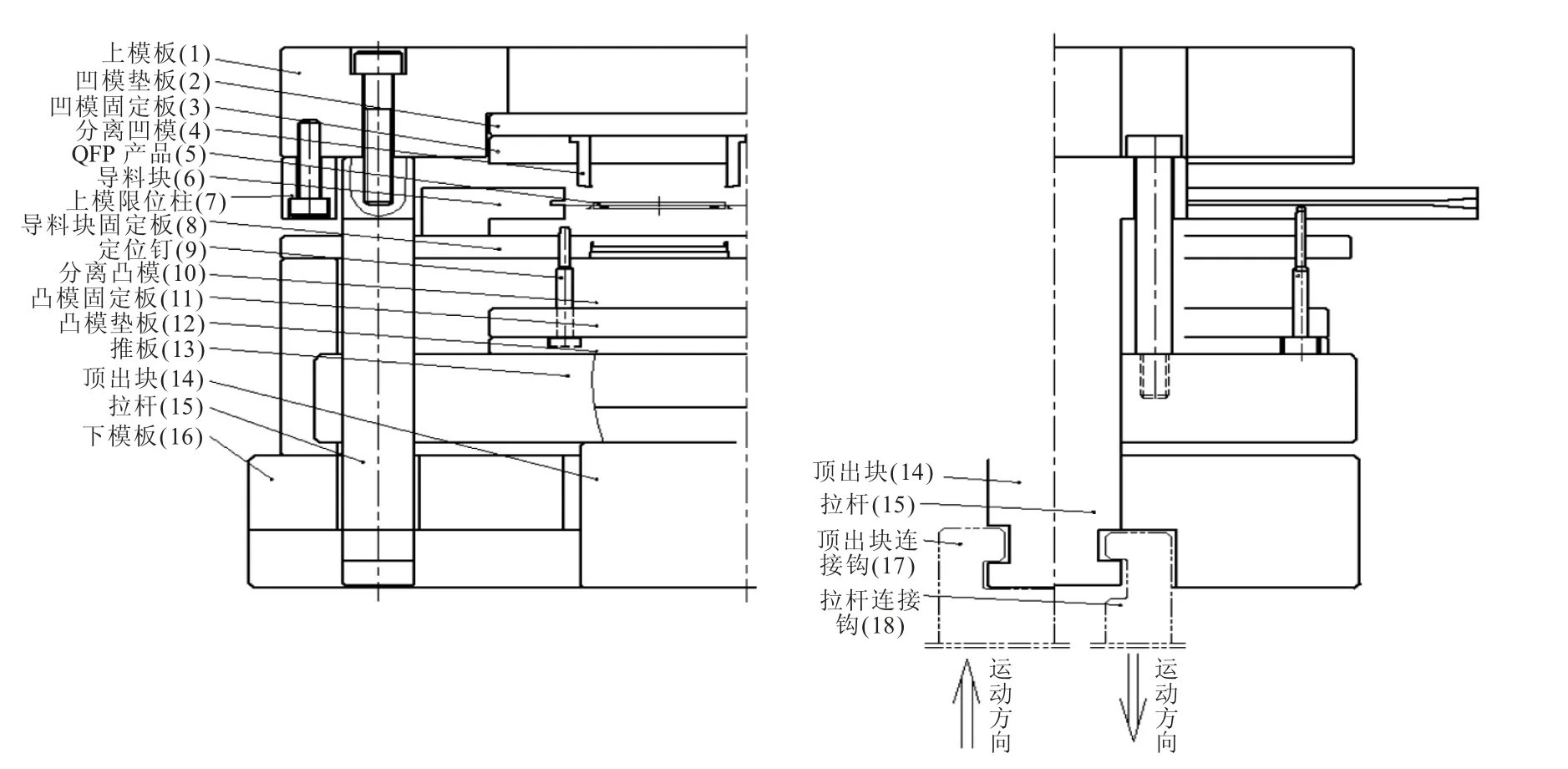
图1 分离模具结构
2 时序关系分析
如图2所示,模具在从“开模位置”向上运行3.2 mm到达“检测位置”的过程中,“检测针”插入引线框架相应的孔内,完成检测和最初的定位。如果产品没有处于正确的位置,检测针就进不了框架相应的孔内,从而触发“检测针传感器”完成检测。在从“检测位置”运行到“分离开始位置”的过程中,上模向下运行4.5 mm,使“分离凹模”(件4)到达产品的分离位置,同时下模继续向上运行5.8 mm,使“分离凸模”(件10)含住产品的下胶体,完成分离动作前的准备工作。“分离凸模”(件10)从“分离开始位置”继续向上推动1.5 mm,切断引线框架和产品的连接部分(tiebar),把产品从引线框架上分离。然后,模具会处于一种保持状态,等待吸盘从模具中吸出分离后的产品,待产品从模具中吸出后,模具才会复位,从而完成一个冲切循环。
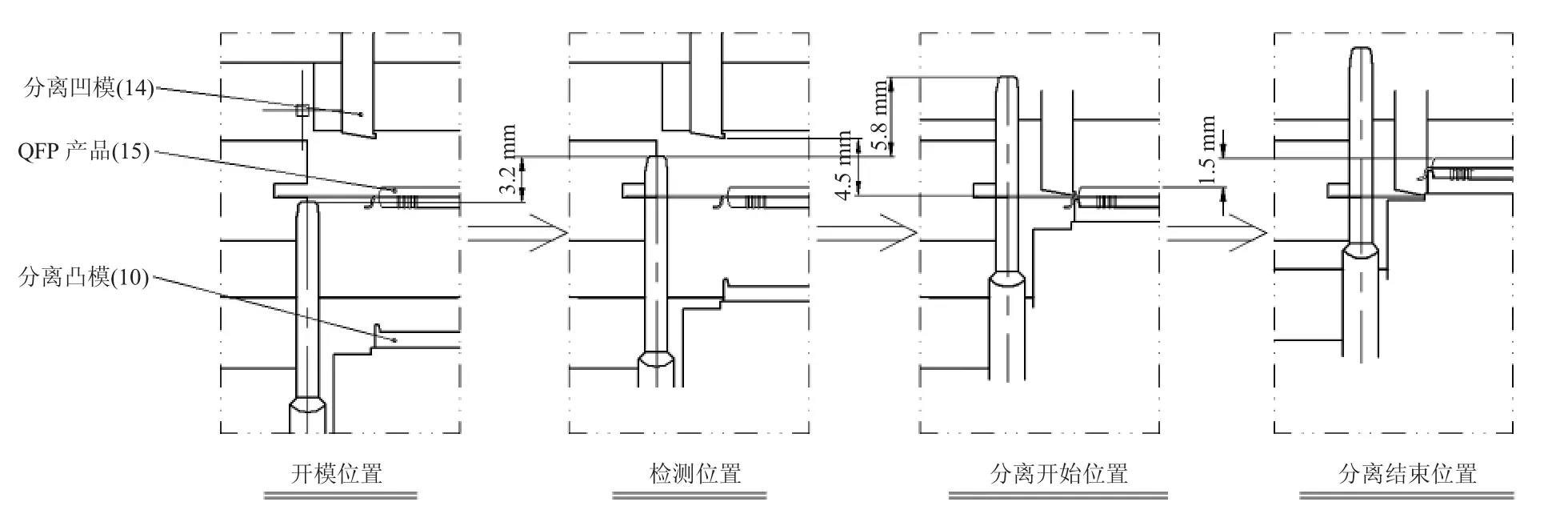
图2 时序关系分析图
3 凸轮时序设计
有了时序关系分析,就可以设计实现时序关系的凸轮机构。其中最关键的是要绘制凸轮时序图,如图3所示。除了要满足动作之间的逻辑关系,还需要分配好每个动作所花费的时间。假设设计的分离速度为60次/min,那么凸轮每转一度所需的时间就是2.78 ms。例如,分配给检测动作的区间角度是0°~36°,那么所分配的时间就是100 ms。合理的时序分配,需要遵循下面3个原则:
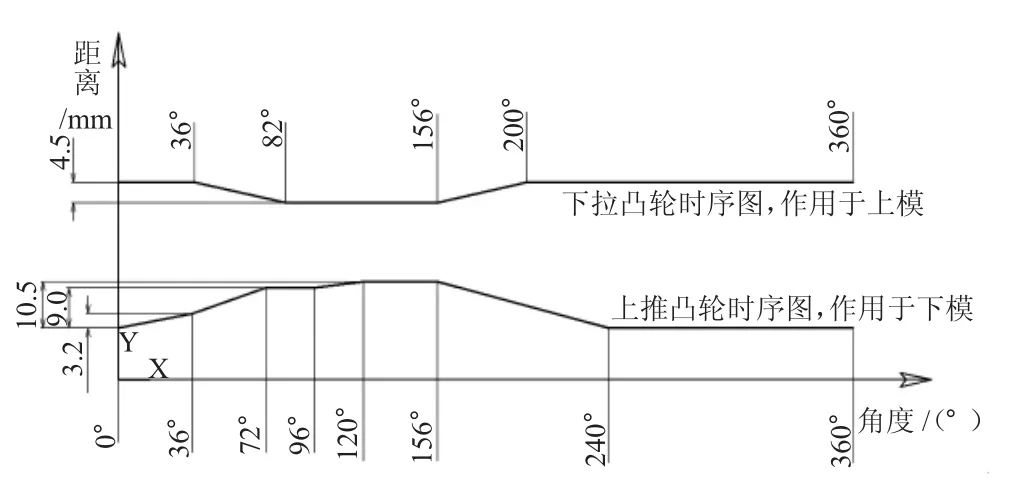
图3 凸轮时序图
(1)如果从动件需要做逻辑判断,譬如说检测位传感器需要给出检测信号时,需要给从动件留出足够的信号检测及反馈时间;
(2)避免从动件运行过程中出现过大的压力角,每种类型的加速度曲线都有最大压力角限制;
(3)需要考虑其他部件执行所需要的时间。譬如上推凸轮中的120°~156°区间是模具的保持段,在这段时间内模具保持产品的分离状态不动,以配合装置的吸盘从模具中吸出产品。
4 凸轮从动件运动规律的选择
在选择凸轮从动件运动规律时,应该避免由于速度突变引起刚性冲击和加速度突变引起的柔性冲击。在目前常用的多项式运动规律和组合运动规律中,要求最大速度、最大加速度、最大跃度都是最小值的运动规律是没有的,应根据不同的情况进行选择,但需遵循下列原则:
(1)高速轻载,优先选择加速度比较小的改进梯形运动规律;
(2)低速重载,优先选择速度比较小的改进等速运动规律;
(3)中速中载,优先选择速度、加速度、跃度都比较合适的改进正弦加速度运动规律。
在本文中,选择的是改进正弦加速度运动规律,因为这种运动规律无冲击,行程始末采用周期较短的正弦加速度,同时行程中部速度和加速度变化比较平缓,速度及转矩小,比较适合模具的负荷较小,速度也相对不高,但要求运行平稳。变形正弦加速度区间行程公式如式(1):
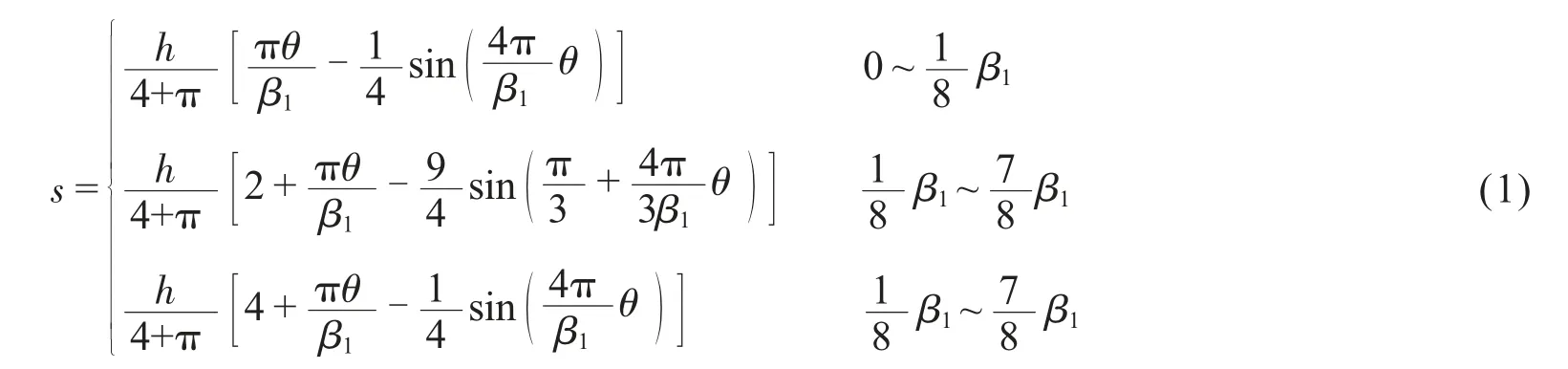
式(1)中,s为凸轮的行程,β1为凸轮运行的区间角度,h为凸轮的升程或回程,θ为凸轮运行的角度。
5 用Pro/e软件自动生成凸轮轮廓曲线
以驱动上模的下拉凸轮为例,从参数规划开始,利用Pro/e强大的参数化能力,设计一个由布局驱动的单停留改进正弦加速度盘型凸轮。
5.1 参数规划
Pro/e通过“布局”来定义参数和参数的传递。在“布局”中,以概念的方式来定义参数和注释零件,通过图表和草绘参照,可清晰地建立各项参数和关系。在零件设计中,通过声明“布局”来获取相关的参数,这样可以很好地管理数据,优化设计流程。同时,可通过直接修改“布局”中的参数来驱动零件的更改,实现了自动生成同族零件的功能。如图4、表1所示,利用Pro/e自带的“布局”功能,在“布局”内对凸轮进行参数规划,并对各项参数进行赋值并设置关系。
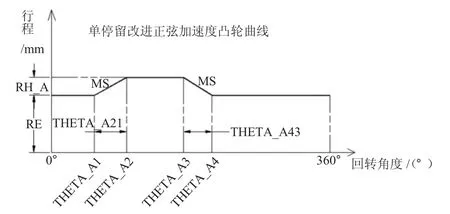
图4 布局及参数定义
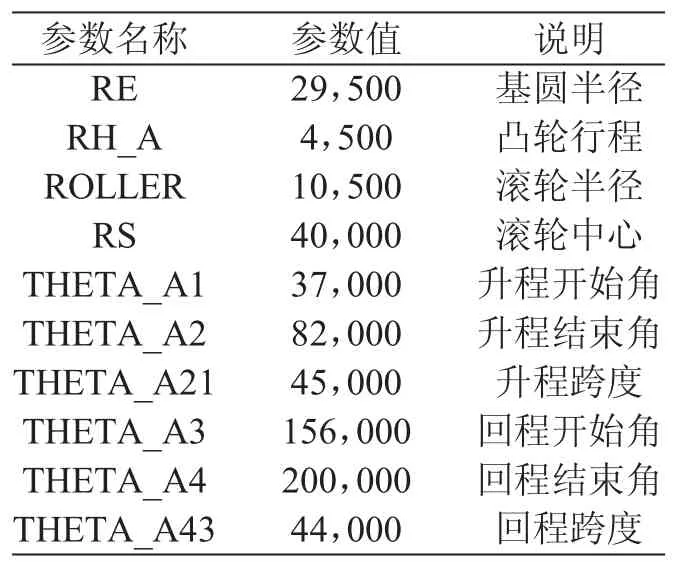
表1 布局参数表及参数关系设置
5.2 凸轮设计
在Pro/e中,使用“零件”模块来设计凸轮,首先在零件模块中声明先前建立的“布局”,来获取“布局”中的参数(同一个布局中的参数可以传递到不同的零件)。在球坐标系中通过关系来生成滚轮中心的运行曲线,也就是凸轮的理论轮廓线,凸轮的实际轮廓是由理论轮廓偏置滚轮半径来实现,如图5所示。下面是生成凸轮理论轮廓线的程序清单:
/*定义升程段曲线第一区间,采用球坐标系(rho,theta,phi)
t1_a=0.125*theta_a21*t /*t1_a,升程区间一,0~1/8 theta_a21
k1=rh_a/(4+pi)
k2=pi*t1_a/theta_a21
/*定义升程段第一区间的曲线方程
rho=rs+k1*(k2-0.25*sin(4*k2*(180/pi))) /*(180/pi)是将弧度转换成度
theta=90
phi=theta_a1+t1_a
/*定义升程段曲线第二区间
t1_a=1/8*theta_a21+3/4*theta_a21*t/*t1_a,升程区间二,(1/8~7/8)theta_a21
k1=rh_a/(4+pi)
k2=pi*t1_a/theta_a21
/*定义升程段第二区间的曲线方程
rho=rs+k1*(2+k2-2.25*sin((pi/3+(4/3)*k2)*(180/pi)))
theta=90
phi=theta_a1+t1_a
/*定义升程段曲线第三区间
t1_a=7/8*theta_a21 +1/8*theta_a21*t/*t1_a,升程区间三,(7/8~1)theta_a21
k1=rh_a/(4+pi)
k2=pi*t1_a/theta_a21
/*定义升程段第三区间的曲线方程
rho=rs+k1*(4+k2-1/4*sin(4*k2*(180/pi)))
theta=90
phi=theta_a1+t1_a
/*定义回程段曲线第一区间
t1_a=1/8*theta_a43*t /*t1_a,回程区间一,(1~7/8)theta_a43
k1=rh_a/(4+pi)
k2=pi*t1_a/theta_a43
/*定义回程段第一区间的曲线方程
rho=(rs+rh_a)-k1*(k2-1/4*sin(4*k2*(180/pi)))
theta=90
phi=theta_a3+t1_a
/*定义回程段曲线第二区间
t1_a=1/8*theta_a43+3/4*theta_a43*t /*t1_a,回程区间二,(7/8~1/8)theta_a43
k1=rh_a/(4+pi)
k2=pi*t1_a/theta_a43
/*定义回程段第二区间的曲线方程
rho=(rs+rh_a)-k1*(2+k2-2.25*sin((pi/3+(4/3)*k2)*(180/pi)))
theta=90
phi=theta_a3+t1_a
/*定义回程段曲线第三区间
t1_a=7/8*theta_a43+1/8*theta_a43*t /*t1_a,升程区间三,(1/8~0)theta_a43
k1=rh_a/(4+pi)
k2=pi*t1_a/theta_a43
/*定义回程段第三区间的曲线方程
rho=(rs+rh_a)-k1*(4+k2-1/4*sin(4*k2*(180/pi)))
theta=90
phi=theta_a3+t1_a
6 结束语
由于是通过程序直接生成凸轮轮廓,消除了通常通过取点方式来拟合所生成轮廓的误差。在实际加工中,CNC或线切割工序可以直接调用Pro/e文档来加工凸轮。在本文所涉及的QFP类分离模具中,由于时序关系是固定的,使用了一对凸轮机构来实现对原有伺服系统的替代。实际生产中该凸轮机构运行稳定可靠,完全能够满足使用要求。说明在某些时序固定的情况下,用凸轮机构取代昂贵的伺服系统来实现特定的运动要求,是完全可以实现的。
