利用参数自适应多点最优最小熵反褶积的行星轮轴承微弱故障特征提取

王朝阁 李宏坤 胡少梁 胡瑞杰 任学平

摘要： 针对行星轮轴承故障振动信号受复杂传递路径、强背景噪声和齿轮振动干扰的影响，导致故障特征微弱难以提取的问题，提出一种参数自适应的多点最优最小熵反褶积（parameter adaptive multipoint optimal minimum entropy deconvolution adjusted，PA?MOMEDA）的行星轮轴承微弱故障诊断方法。为克服MOMEDA依赖人为经验选取主要影响参数的不足，建立多目标优化新指标，通过粒子群算法优良的寻优特性来自动确定最佳的影响参数，使用参数优化的MOMEDA对行星轮轴承故障信号进行最佳解卷积运算。针对MOMEDA解卷积信号存在严重边缘效应的问题，设计一种波形延伸策略对解卷积信号进行自适应补偿，提高了MOMEDA对微弱故障冲击特征的解卷积性能。对提升的解卷积信号进行包络解调处理，即可从其包络谱中提取到明显的故障特征频率。通过行星轮轴承故障仿真和工程实验数据分析表明，相比传统的MOMEDA方法、MCKD方法和快速谱峭度方法，该方法能成功地提取微弱的故障冲击特征且更加明显，提高了行星轮轴承故障诊断的准确性和鲁棒性。

关键词： 故障诊断; 行星齿轮箱; 行星轮轴承; 特征提取; 多点最优最小熵反褶积（MOMEDA）

中图分类号： TH165+.3; TH133.33    文献标志码： A    文章编号： 1004-4523（2021）03-0633-13

DOI：10.16385/j.cnki.issn.1004-4523.2021.03.022

引  言

行星齿轮箱具有传动平稳、体积小巧、减速比大和效率高等优点，已被广泛应用于直升机、重型卡车、风力发电和舰船等大型复杂机械设备中[1]。行星轮轴承作为齿轮箱中关键零部件，不仅为行星齿轮提供可靠稳定的支撑，而且还承担着较大的工作载荷。然而，行星齿轮箱的工作环境通常比较恶劣，长期运行在高负荷、强冲击和高污染的工况下，极易导致行星轮轴承出现点蚀、擦伤、脱落和断裂等局部损伤。行星轮轴承一旦出现故障，将直接造成齿轮箱运行状况恶化，继而导致设备及整个动力传输系统受到毁坏，后果极为严重[2]。因此，研究有效可靠的行星轮轴承故障诊断技术对于保证设备稳定安全运行十分必要。

通常，行星轮轴承内圈固定在行星轮轴上，外圈安装在行星轮轴孔中，因此行星轮轴承不仅围绕行星轮轴自转，而且还随行星架公转。然而，这种独特的运转方式使行星轮轴承的故障诊断面临诸多棘手的问题：（1）由于行星轮轴承随着行星架进行公转，故障信号到达传感器的传递路径随时间不断改变，使故障信号呈现出明显的非线性;（2）故障振动信号经历复杂传递路径后能量严重衰减，故障特征变得微弱且被强噪声掩盖;（3）在运转过程中，故障振动信号与齿轮啮合振动之间相互耦合、相互干扰，导致轴承故障特征很难辨识。因此，消除传递路径与齿轮啮合影响，增强微弱故障特征信息是行星轮轴承故障检测与识别急需解决的关键问题。

目前，关于行星轮轴承故障诊断方面的研究比较少，学者们大多是针对传统的平行轴齿轮箱滚动轴承故障诊断进行研究，提出了快速谱峭度、经验小波变换和共振稀疏分解等方法[3?5]，并取得了较好的应用效果。然而，直接使用上述方法对行星轮轴承故障信号进行分析，往往不能取得令人满意的结果，这是由于行星轮轴承的信号特征非常复杂。为了提取行星轮轴承故障特征，Fan等[6]将传感器直接安装在行星架上获取轴承故障信号，这种方式虽然可以避免传递路径和齿轮啮合振动的影响，但在实际工程中由于费用和设计的局限性，内置传感器并不适用于每个行星齿轮箱。齿轮箱中故障冲击信号向外传递的过程可看作是冲击信号与传递通道的线性卷积过程，原始故障冲击信号的提取则可看作是解卷积处理。Endo等[7]首次将最小熵反褶积（minimum entropy deconvolution，MED）应用于齿轮箱故障检测，取得了良好的效果。但 MED方法在解卷积过程只能突出局部几个故障脉冲成分，并不能反映故障的真实情况。同时，在迭代过程中寻找的滤波器并不一定是全局最优滤波器[8]。随后，McDonald等[9]在MED的基础上提出了最大相关峭度解卷积（maximum correlation kurtosis deconvolution， MCKD）方法，实现了对周期性脉冲的解卷积。但该算法中故障周期、滤波器长度、平移次数等参数的选取较为困难，若参数选取不当将产生误诊现象[10?11]。为了弥补MED和MCKD方法的局限性，McDonald等[12]提出了多点优化最小熵反褶积修正 （multipoint optimal minimum entropy deconvolution adjusted，MOMEDA） 算法，它是一種新的非迭代盲解卷积增强技术。该算法引入时间目标向量来确定待解卷积脉冲序列的位置和权重，并应用多点峭度值确定故障发生周期，从而实现对连续多点故障冲击脉冲的提取[13?14]。然而，在MOMEDA算法中故障周期搜索范围和滤波器长度的选取完全依赖人为主观经验，这很大程度上影响故障脉冲序列提取的准确性。此外，解卷积信号存在严重的边缘效应，特别是当滤波器长度较大时，会造成信号中重要的故障信息丢失，从而限制了MOMEDA的应用。

针对上述问题，本文提出一种参数自适应的多点最优最小熵反褶积（parameter adaptive multipoint optimal minimum entropy deconvolution adjusted，PA?MOMEDA）方法。首先通过建立多目标优化新指标来自适应地确定故障周期搜索范围和滤波器长度，然后根据信号局部特点，设计一种波形延伸策略对解卷积后的信号进行补偿，从而有效地克服边缘效应的影响，提高了MOMEDA对微弱故障冲击成分的解卷积增强性能。信号仿真和行星轮轴承实验数据分析表明，该方法能有效、准确地实现行星轮轴承微弱故障的识别与诊断，为工程实际应用提供了一种新思路。

1 参数自适应的MOMEDA算法

1.1 MOMEDA原理

由于行星齿轮箱复杂的运转方式，实际的行星轮轴承故障信号将包含多个分量，则获取的行星轮轴承故障信号可表示为

式中  为采集的振动信号;为故障产生的脉冲序列;为系统其他波动干扰;为背景噪声成分;，和分别为不同输入对应的系统传递函数。

MOMEDA的核心思想是通过非迭代的形式寻求全局最佳FIR滤波器，然后进行解卷积运算提取故障脉冲序列，并最大限度消除背景噪声和其他干扰成分的影响。解卷积的过程为

式中  表示信号的长度;为滤波器的长度。

为了提取振动信号中连续的周期性脉冲序列，MOMEDA算法在解卷积时将多点D?范数作为目标函数，通过求解多点D?范数的最大值使解卷积效果达到最佳[12]。即：

式中  为目标向量，它决定待解卷积目标脉冲的位置和权重。解卷积的效果取决于对冲击序列定位的准确度。

MOMEDA的求解可以通过对滤波器系数进行微分求解式（4）极值问题。

式中  为样本的一个脉冲;是用于扩展目标向量的窗口函数。在实际应用中，由于故障周期不一定是采样周期的倍数，因此非整数应该进行四舍五入取整。为了选取合适的并度量提取脉冲序列的效果，引入了多点峭度（Mkurt）的概念[13]

在实际应用中，通过设定故障周期的预测范围和步长，逐步迭代得到目标向量，当中的脉冲间隔等于故障周期时，Mkurt谱中会出现明显的峰值，根据最大峰值所对应的周期求解得到的输出信号即为提取的故障冲击序列。

1.2 输入参数的自适应选取

MOMEDA算法的输入参数包括窗函数、滤波器长度和故障周期的搜索区间。输入参数的正确选取对提高MOMEDA的性能至关重要。

（1）窗函数。窗函数用于进一步扩展目标向量，它能够提高频谱的清晰度和故障冲击序列提取的准确性。考虑到计算效率和解卷积增强效果，本文采用长度为3的矩形窗。

（2）滤波器长度。直接影响着脉冲序列提取效果。为了确保提取到的冲击序列能覆盖到故障的整个频带，滤波器长度应该满足[10]

式中  为信号的采样频率，为故障特征频率。然而，增加滤波器长度会使解卷积信号的长度减少为，这会造成故障信息的严重丢失。同时，增加将消耗更多的计算时间。因此，本文设置滤波器长度选取范围为。

（3）故障周期搜索范围。和分别为故障周期搜索的初始值和最终值。根据行星轮轴承特征频率计算公式，可获得各单元（内圈、外圈和滚动体）特征频率和故障周期（为内圈故障周期;为外圈故障周期;为滚动体故障周期）。由于轴承各单元间存在关系，所以得到。文献[14]已证明当搜索区间包含故障周期时，最终值不会对故障冲击序列的提取产生影响，因此，根据行星齿轮箱的实际运行情况取。在本文中，针对行星轮轴承不同单元的故障形式，分别在区间范围内对故障周期的初始值进行选取。

（4）优化参数和。为了选取最优的参数组合，本文构造多目标优化的新指标来自适应地确定滤波器长度和故障周期搜索初始值。时域中，采用自相关函数最大值（autocorrelation function maximum，AFM）的均方根来衡量解卷积后信号中包含的周期性故障冲击成分[15]。该指标的核心是自相关函数，若解卷积后信号中的主要成分为噪声，其自相关函数会很快衰减为0，AFM值必然非常小且接近0;若解卷积后信号中含有明显的周期性故障冲击成分，其自相关函数是周期性的，AFM值较大。因此，用AFM指标来衡量解卷积运算对故障冲击序列的提取效果，其表达式如下

式中  为自相关函数的最大值;为要计算的自相关函数中的延迟数。

若解卷积信号中含有越多的故障冲击成分，对应包络谱中会出现越显著的故障特征频率。包络谱将会严重地偏离正态分布，最终导致包络谱峭度（envelope spectrum kurtosis，ESK）值变大。因此，用ESK指标来衡量解卷积信号在频域中所含故障频率信息的丰富程度。信号的ESK计算公式为：

式中  表示包络谱的幅值，为的均值。

本文将解卷积后信号的时域AFM和频域ESK联合起来构建一个新的复合指标（composite index，CI），并将其作为MOMEDA中参数优化的目标函数，其定义如下

通过粒子群优化方法（particle swarm optimization，PSO）[16?17]选取CI的最大值來自适应地确定MOMEDA中最佳输入参数组合，从而提升MOMEDA对行星轮轴承微弱故障冲击的解卷积能力。

1.3 信号波形延伸策略

MOMEDA解卷积后的信号存在边缘效应，导致信号长度相比原始信号减少了很多样本点。针对该问题，根据解卷积信号左边界处的局部特性，采用信号波形延伸方法，将解卷积信号恢复到与原信号相同的长度，从而有效地保留解卷积信号的周期性。信号波形延伸方法的具体步骤如下：

步骤1：寻找信号的极值点。确定解卷积信号所有的局部极值点及其位置。

步骤2：确定对称中心。根据信号在左边界的局部特征来确定信号延伸时的对称中心。设a，b和c分别为信号的前三个局部极值点，若，如图1（a）所示，则选取极值点a作为对称中心;若，如图1（b）所示，则选取极值点b作为对称中心;若，如图1（c）所示，则选取极值点a作为对称中心;若，如图1（d）所示，则选取极值点b作为对称中心。

步骤3：信号波形延伸。选取对称中心后面一定数量的样本点作为扩展对象，然后取对称中心的镜像，得到扩展的信号波形，如图1中红实线所示。

1.4 参数自适应的MOMEDA

基于上述讨论，首先构建新的复合指标CI作为MOMEDA中参数优化的目标函数，利用PSO优良的寻优特性，在无任何先验知识的条件下，自动选取最佳影响参数;然后，采用波形延伸策略将最佳解卷积后的信号自适应地恢复到与原始信号相同的长度，从而保证其完整的周期性。PA?MOMEDA算法在行星轮轴承微弱故障诊断中的具体实现步骤如下：

步骤1：获取行星轮轴承故障振动信号;

步骤2：计算轴承各元件故障周期，根据1.2节参数选取原理，设置故障周期初始值的搜索范围和最终值，滤波器长度取值范围;选取长度为3的矩形窗作为窗函数;

步骤3：初始化PSO各项数值，本文设置粒子个数为30，最大迭代次数为20，恒惯性权重为0.9，学习因子为1.5。以参数组合作为粒子，随机产生一定数目的参数组合作为粒子初始位置，随机初始化每个粒子的移动速度;

步骤4：以复合指标CI作为适应度函数，比较个体与种群的适应度值，并更新个体和种群全局最优值。通过下式更新种群粒子的速度与位置，循环迭代，转到步骤3，直到满足最大循环次数，获取最终的优化参数组合;

步骤5：利用参数优化后的MOMEDA对轴承故障信号进行解卷积运算。根据1.3节波形延伸策略，对解卷积后信号进行波形延伸，得到提升信号;

步骤6：将提升的解卷积信号做包络解调处理，提取故障特征频率并与理论值对比，从而判别行星轮轴承的故障类型。诊断方法的流程如图2所示。

2 仿真信号分析

2.1 行星轮轴承外圈故障模型

为检验所提方法，建立行星轮轴承外圈故障信号模型。该信号模型由轴承故障冲击振动，齿轮啮合振动、其他零部件正常旋转振动和随机噪声这4种成分构成，其方程如下

当行星轮轴承外圈出现故障时，在运转过程中会产生一系列丰富的冲击信号，并激起系统其他元件的共振;同时，由于系统阻尼的存在，冲击信号会衰减[18]。根据行星轮轴承独特的运转方式，综合考虑轴承自转引起的载荷区通过效应、齿轮啮合力与故障点冲击力作用方向角变化以及轴承公转引起的传递路径变化等调制作用，建立的行星轮轴承外圈故障振动模型如下

式中  为脉冲的数量;代表振动传递路径和激振力方向角时变效应引起的调幅作用;和为幅值;为外圈相对于行星轮轴的自传频率;为行星架的旋转频率;为指数衰减脉冲，为轴承系统的衰减系数;为轴承元件的共振频率;为连续两次脉冲发生的时间间隔，轴承故障特征频率为;为第次冲击的微小误差，使其服从标准差为的正态分布。

行星齿轮箱运转时，受行星轮通过效应的影响，啮合点处的振动信号将被调制，因此齿轮的啮合振动可表示为

式中  为幅值，为齿轮啮合频率。

行星齿轮箱通常呈现周期性运转，所以用高、低谐波分量分别表示不同部件的旋转振动

为添加到仿真信号中信噪比为SNR=-6 dB的高斯白噪声。各仿真信号的参数值如表1所示。

2.2 行星轮轴承故障仿真实验

仿真信号采样频率设置为5120 Hz，所用分析数据为15360点。把表1中数值分别代入式（21）?（23）中，获得外圈故障冲击、齿轮啮合振动、其他零部件旋转振动和随机噪声如图3所示。图4为混合仿真信号及其FFT频谱和包络谱。由图4可知，轴承故障激发的微弱周期性冲击完全淹没在背景噪声中，从其FFT频谱和包络谱中未能提取与外圈相关的特征频率。因此，传统的时域、频域和包络解调方法对行星轮轴承微弱故障失去诊断能力。

为提取轴承外圈微弱的故障冲击特征，按1.2节参数选取原理，设置故障周期初始值和濾波器长度的取值范围分别为和。本文方法处理结果如图5所示。图5（a）为解卷积信号的CI值随种群进化代数的变化关系。由图5（a）可知，PSO寻优过程中种群进化到第7代得到解卷积信号最大的CI值，搜寻的最佳参数组合为[100，1485]。最佳解卷积信号及其包络谱如图5（b）和（c）所示。可以看到，解卷积信号波形中清晰地出现了等间隔周期性冲击特征，同时信号的长度与原始信号相等，从而有效地克服了边缘效应的影响，保存了重要的故障信息;在对应的包络谱中外圈故障特征频率及其倍频处呈现较突出的谱峰。由此可判断行星轮轴承外圈出现了故障，这与仿真结果相一致。

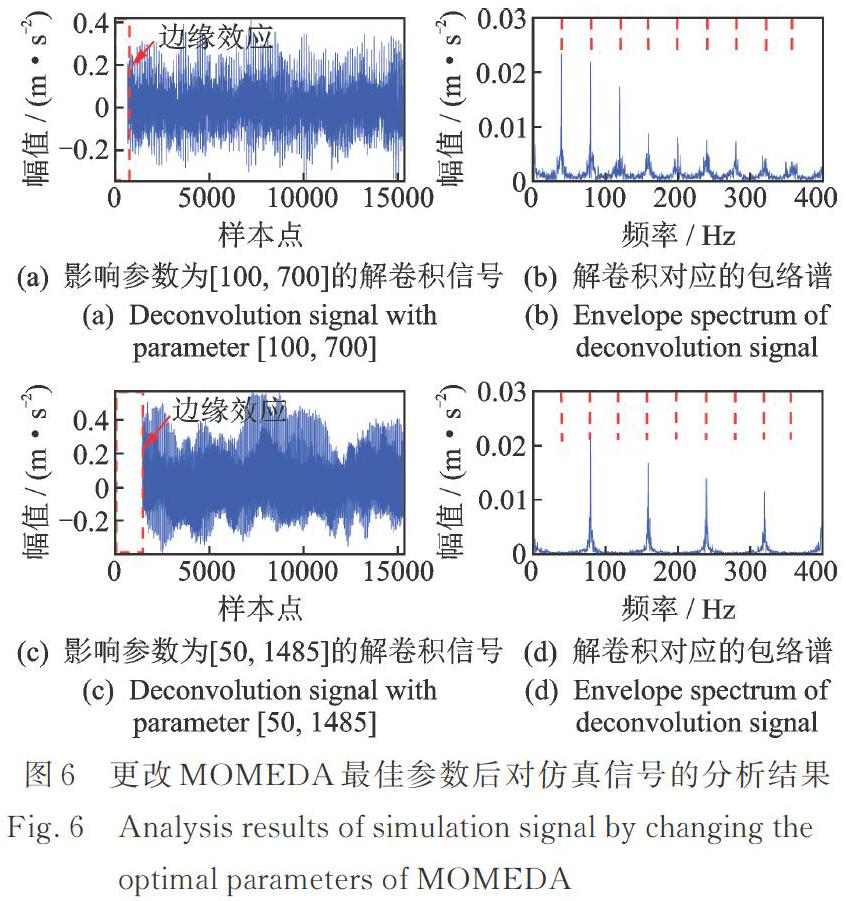
为验证本文方法获取最优参数组合的准确性，随机更换中的某一参数，使用更换参数后的MOMEDA对图4（a）中的仿真信号进行处理。图6（a）和（b）是将最优参数组合[100，1485]中的滤波器长度更改为700得到的结果。与图5（b）相比，原始MOMEDA方法存在严重的边缘效应，解卷积后信号的长度明显缩短。同时，在图6（b）对应的包络谱中倍频处谱线并不明显，且谱线的整体幅值低于图5（c）。图6（c）和（d）是将最优参数组合[100，1485]中的故障周期初始值更改为50获得的结果，解卷积信号的左端同样出现了边缘效应，其包络谱中提取到的频率成分为85.3 Hz及其倍频。可见，噪声严重时更改最佳故障周期初始值后，原始MOMEDA方法未能成功提取到轴承外圈故障特征。上述结果表明，主观随机的参数选取对解卷积效果会产生严重的影响，甚至提取不到目标频率成分，而本文方法能够有效避免这一现象，实现故障冲击的最优解卷积。

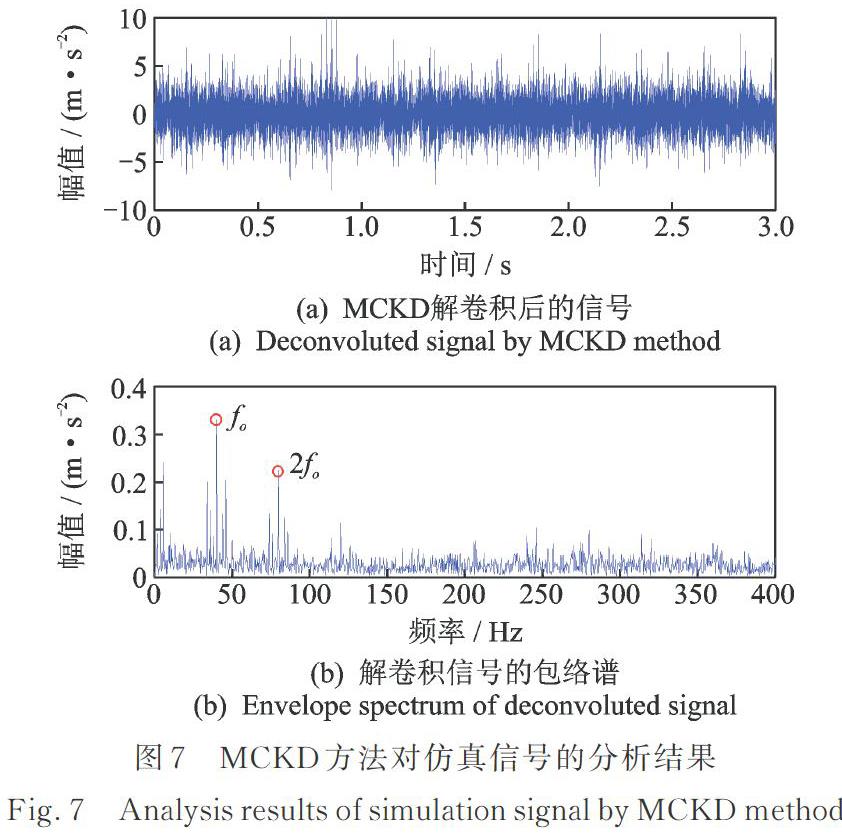
作为对比，分别利用MCKD方法和FSK方法对图4（a）中的仿真信号进行处理。图7为MCKD方法处理的结果。由图7可知，经MCKD解卷积后信号波形中呈现出微弱的冲击特征，但这些冲击的规律性并不显著，包络谱中仅能看到外圈特征频率及倍频。图8为FSK方法滤波后的结果。由图8可知，滤波后信号的波形中无明显的周期性冲击特征，包络谱中也未提取到外圈特征频率。对比图5中PA?MOMEDA分析结果，MCKD方法和FSK方法都难以提取到明显的轴承外圈故障特征信息，处理结果并不理想。

为进一步验证PA?MOMEDA方法在微弱特征提取中的优势，采用时域和频域指标来综合地评价其性能。时域采用一阶的相关峭度（first?shift correlated kurtosis，CK1）[19]来评价信号中周期性冲击特征的增强效果，其表达式如下

式中  为被分析信号;为故障周期。此外，频域采用改进的故障特征系数（fault feature coefficient，FFC）指标[20]评估包络谱中故障特征频率对应谱线的清晰度，其表达式为

式中  为轴承故障特征频率;为被分析信号包络谱的幅值。表2为PA?MOMEDA与MOMEDA，MCKD和FSK方法处理混合故障仿真信号的对比。由表2可知，PA?MOMEDA具有较大的CK1和FFC值，这表明本文方法可以更加完整、准确地提取外圈微弱故障特征信息，具有理想的分析效果。

3 实验验证

3.1 实验说明

为验证所提方法在实际行星轮轴承故障诊断中的有效性，在Spectra Quest公司设计的工业动力传动故障诊断综合实验台上开展行星轮轴承故障实验，实验系统如图9所示。该实验台主要由交流驱动电机、行星齿轮箱、2级平行轴齿轮箱与磁力加载器等组成。行星齿轮箱参数如表3所示。本实验以行星齿轮箱中型号为HK1010的行星轮轴承为研究对象。表4为行星轮轴承的结构参数。实验时在行星轮轴承的外圈和滚针上人为地进行损坏分别来模拟外圈和滚动体局部损伤。行星轮轴承故障件如图10所示。本次实验使用PCB352C33型加速度传感器（量程范围：±50g，频率范围：0.5?10 kHz，灵敏度为100 mV/g）采集故障振动信号。传感器固定在行星齿轮箱壳体顶部的垂直、水平和轴向的测点上。选用DT9837数据转换仪和一台安装DAQ软件的电脑作为本次实验的数据采集系统。实验时，行星齿轮箱恒定输入转速为1380 r/min，数据采样频率设置为5120 Hz，所用数据长度为15360点。在该实验条件下，计算行星齿轮箱中齿轮与行星轮轴承各元件特征频率如表5所示[21]。

3.2 实测信号分析

3.2.1 行星轮轴承外圈故障信号

图11为垂直方向传感器收集到的行星轮轴承外圈故障信号及其FFT频谱和包络谱。由图11可知，外圈故障时域波形中难以观察到有规律的冲击特征;FFT频谱中频率成分主要集中在500?1500 Hz内，在低频段找不到与轴承外圈损伤相关的特征频率;包络谱中也未呈现出相应的外圈故障特征频率，噪声与其他无关干扰频率较为突出。因此，通过传统的时、频域分析和包络谱方法无法从原始故障信号中提取表征行星轮轴承健康状态的特征信息。

为揭示隐藏在动态信号中的因轴承外圈损伤所产生的微弱故障征兆，利用本文方法对轴承外圈故障信号进行分析。按1.2节参数选取原理，故障周期初始值和滤波器长度取值范围分别设置为和。根据行星轮轴承故障周期理论计算公式得到：。图12为本文方法处理的结果。由图12（a）可知，种群进化到第5代时获取解卷积信号的最大CI值，搜寻的最优参数组合为[147.27， 1902]。图12（b）和（c）为最佳解卷积信号及其包络谱。可以看到，通过解卷积运算，隐藏在动态信号中的周期性冲击特征被清晰地揭露出来，噪声及其他干扰被有效地去除。同时，解卷积信号未出现边缘效应，信号长度与原始信号相等，从而更好地保留了信号中重要的微弱特征信息;包络谱中外圈故障特征频率及其倍频处具有较明显的谱线，且在整个频谱中占主导地位。因此，上述分析结果表明行星轮轴承外圈出现了故障，这与实验设置一致。

为检验获取的最佳参数组合在实际行星轮轴承外圈故障信号中的可靠性，随机更换中的某个参数，利用更改参数后的原始MOMEDA方法对外圈故障信号进行处理。图13（a）和（b）是将最优参数组合[147.27， 1902]中的滤波器长度更改为1000得到的结果。与图12（b）相比，原始MOMEDA方法解卷积信号的左端出现了严重的边缘效应，导致部分周期性冲击成分丢失。同时，在图13（b）对应的包络谱中外圈故障特征频率及部分倍频处的谱线并不明显，且谱线的整体幅值低于图12（c）。图13（c）和（d）是将最优参数组合[147.27， 1902]中的故障周期初始值更改为50后的结果，解卷积信号的左端同样出现了较严重的边缘效应;此外，对应包络谱中识别到的频率为85.3 Hz及其倍频成分。由此可知，更改最佳故障周期初始值后，原始MOMEDA方法未能成功提取微弱的外圈故障特征。

作为对比，分别采用MCKD方法和FSK方法对轴承外圈故障信号开展分析。图14为MCKD方法的处理结果。可以看出，MCKD仅提取出部分冲击成分，同时在图14（b）的包络谱中，可见许多幅值较大的噪声干扰频率，外圈故障特征频率及其倍频不易被识别。图15为FSK方法的分析结果。由图15可知，经FSK滤波后信号中出现了强弱不等的冲击特征，但这些冲击的周期性并不清晰。在图15（c）滤波信号的包络谱中，除了明显的行星架转频外，轴承外圈故障特征频率成分未被提取。由对比可知，MCKD方法和FSK方法都难以将行星轮轴承外圈故障产生的微弱周期性冲击特征清晰地提取出来，处理结果不如图12中PA?MOMEDA方法理想。表6为PA?MOMEDA与MOMEDA，MCKD和FSK方法的直观对比。从表6可知，PA?MOMEDA所对应的CK1和FFC值最大，这表明本文方法在轴承外圈微弱故障特征提取中具有更大的优势。

3.2.2 行星轮轴承滚动体故障信号

图16为垂直方向传感器检测到的行星轮轴承滚动体故障信号及其FFT频谱和包络谱。由图16可知，表征滚动体故障的周期性冲击和特征频率被信号中的强噪声所淹没，从其时域波形、FFT频谱及包络谱中都难以提取出相应的滚动体故障特征信息。因此，傳统的时、频域分析和包络谱方法无法检测出微弱的行星轮轴承滚动体故障。

采用本文方法，分别设置故障周期初始值和滤波器长度的取值范围为和。图17为PA?MOMEDA方法得到的最优解卷积结果。图17（a）中，种群进化到第7代获得解卷积信号的最大CI值，搜寻到的最优参数组合为[234.3， 1348]。图17（b）为最佳解卷积信号，可清晰观察到等间隔的周期性冲击特征，同时，解卷积信号左端未出现边缘效应，有效地避免了微弱故障特征信息的丢失。在图17（c）解卷积信号的包络谱中，滚动体故障特征频率及其倍频处呈现出较明显的谱线。因此，上述分析结果表明行星轮轴承滚动体出现了故障，这与实验设置相符。

为验证最佳参数组合在实际行星轮轴承滚动体故障信号中的可靠性，随机更改中的某一参数，利用参数更改后的原始MOMEDA算法对滚动体故障信号进行处理。图18（a）和（b）是更改最优参数组合[234.3， 1348]中的滤波器长度为1000得到的结果。与图17（b）相比，原始MOMEDA方法存在严重的边缘效应。同时，在对应的包络谱中滚动体故障特征频率的倍频成分变得模糊，且谱线的整体幅值低于图17（c）。图18（c）和（d）是将最优参数组合[234.3， 1348]中的故障周期初始值更改为50后的结果，其中解卷积信号左端出现了明显的边缘效应;此外，在其包络谱中提取到的频率成分为61.2 Hz及其倍频。由此可知，更改最佳故障周期初始值后，原始MOMEDA方法未能成功提取微弱的滚动体故障特征。

作为对比，分别采用MCKD方法和FSK方法对滚动体故障信号开展分析。图19为MCKD方法处理的结果。由图19可知，解卷积信号的波形中出现了部分冲击分量，对应的包络谱中虽然在滚动体故障特征频率及其倍频处存在谱线，但整个谱图中其他干扰频率的幅值较大，妨碍对故障特征的辨识。FSK方法分析结果如图20所示，滤波后信号中可见一些冲击特征，对应的包络谱中，行星架转频及其倍频能够被识别，但滚动体故障特征频率未能显现，该方法无效。与本文方法对比（图17），MCKD方法虽可以提取部分故障冲击特征，但其在噪声抑制和抗干扰方面表现不足，此外，FSK方法無法将微弱的滚动体故障特征有效地提取出来，不具有诊断能力。表7为PA?MOMEDA与MOMEDA，MCKD和FSK方法的直观对比。由表7可知，PA?MOMEDA方法具有最大的CK1和FFC值，这再次证明本文方法在微弱滚动体故障特征识别中具有更突出的优势。

4 结  论

本文提出了一种参数自适应的MOMEDA故障诊断方法，解决了行星轮轴承微弱故障特征难以提取和识别的问题。通过行星轮轴承故障仿真和工程实验数据的分析可知，该方法能够有效增强微弱的周期性故障冲击特征，在行星轮轴承故障诊断和预测中具有明显的优势。

（1）PA?MOMEDA方法通过构建新的复合指标作为参数寻优的目标函数，利用粒子群算法优良的全局搜索特性自适应地确定最优的影响参数，从而避免参数选取时人为主观因素的干扰，实现最优的解卷积结果。

（2）提出的波形延伸策略能够对解卷积信号进行自适应补偿，使其恢复到与原信号相同的长度，克服了边缘效应的影响，有效地保留了信号中重要的微弱特征信息，从而显著提高了MOMEDA的解卷积增强性能。

（3）通过与传统的MOMEDA，MCKD和快速谱峭度方法对比，本文PA?MOMEDA方法能够提取到更加清晰明显的故障特征频率及其丰富的倍频成分，实现行星轮轴承微弱故障的准确识别与诊断。

参考文献：

[1] 雷亚国， 孔德同， 李乃鹏， 等. 自适应总体平均经验模式分解及其在行星齿轮箱故障检测中的应用[J].机械工程学报， 2014， 50（3）： 64-70.

Lei Yaguo， Kong Detong， Li Naipeng， et al. Adaptive ensemble empirical mode decomposition and its application to fault detection of planetary gearboxes[J]. Journal of Mechanical Engineering， 2014， 50（3）： 64-70.

[2] Wang T， Chu F， Feng Z. Meshing frequency modulation index-based kurtogram for planet bearing fault detection[J]. Journal of Sound and Vibration， 2018， 432： 437-453.

[3] Antoni J， Randall R. The spectral kurtosis： Application to the vibratory surveillance and diagnostics of rotating machines[J]. Mechanical Systems and Signal Processing， 2004， 20： 308-331.

[4] 邓飞跃，强亚文，杨绍普，等. 一种自适应频率窗经验小波变换的滚动轴承故障诊断方法[J]. 西安交通大学学报， 2018， 52（8）： 22-29.

Deng Feiyue， Qiang Yawen， Yang Shaopu， et al. A fault diagnosis method of rolling bearings with adaptive frequency window empirical wavelet transform[J]. Journal of Xi'an Jiaotong University， 2018， 52（8）： 22-29.

[5] 李  星， 于德介， 张顶成. 基于最优品质因子信号共振稀疏分解的滚动轴承故障诊断[J]. 振动工程学报， 2015， 28（6）： 998-1005.

Li Xing， Yu Dejie， Zhang Dingcheng. Fault diagnosis of rolling bearing based on resonance-based sparse signal decomposition with optimal Q-factor[J]. Journal of Vibration Engineering， 2015， 28（6）： 998-1005.

[6] Fan Z， Li H. A hybrid approach for fault diagnosis of planetary bearings using an internal vibration sensor[J]. Measurement， 2015， 64： 71-80.

[7] Endo H， Randall R B. Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter[J]. Mechanical Systems and Signal Processing， 2007， 21（2）： 906-919.

[8] Cheng Y， Zhou N， Zhang W， et al. Application of an improved minimum entropy deconvolution method for railway rolling element bearing fault diagnosis[J]. Journal of Sound and Vibration， 2018， 425： 53-69.

[9] McDonald G L， Zhao Q， Zuo M J. Maximum correlated kurtosis deconvolution and application on gear tooth chip fault detection[J]. Mechanical Systems and Signal Processing， 2012， 33： 237-255.

[10] Miao Y， Zhao M， Lin J， et al. Application of an improved maximum correlated kurtosis deconvolution method for fault diagnosis of rolling element bearings[J]. Mechanical Systems and Signal Processing， 2017， 92： 173-195.

[11] Lyu X， Hu Z， Zhou H， et al. Application of improved MCKD method based on QGA in planetary gear compound fault diagnosis[J]. Measurement， 2019， 139： 236-248.

[12] McDonald G L， Zhao Q. Multipoint optimal minimum entropy deconvolution and convolution fix： Application to vibration fault detection[J]. Mechanical Systems and Signal Processing， 2017， 82： 461-477.

[13] Wang Z， Du W， Wang J， et al. Research and application of improved adaptive MOMEDA fault diagnosis method[J]. Measurement， 2019， 140： 63-75.

[14] Zhou C， Ma J， Wu J， et al. A parameter adaptive MOMEDA method based on grasshopper optimization algorithm to extract fault features[J]. Mathematical Problems in Engineering， 2019， 1971： 1-22.

[15] Chen D， Lin J， Li Y. Modified complementary ensemble empirical mode decomposition and intrinsic mode functions evaluation index for high-speed train gearbox fault diagnosis[J]. Journal of Sound and Vibration， 2018， 424： 192-207.

[16] Trelea I C. The particle swarm optimization algorithm： Convergence analysis and parameter selection[J]. Information Processing Letters， 2003， 85（6）： 317-325.

[17] Cheng Y， Wang Z， Zhang W， et al. Particle swarm optimization algorithm to solve the deconvolution problem for rolling element bearing fault diagnosis[J]. ISA Transactions， 2019， 90： 244-267.

[18] Feng Z，Ma H，Zuo M J. Vibration signal models for fault diagnosis of planet bearings[J]. Journal of Sound and Vibration， 2016， 370： 372-393.

[19] Li Z， Chen J， Zi Y， et al. Independence-oriented VMD to identify fault feature for wheel set bearing fault diagnosis of high speed locomotive[J]. Mechanical Systems and Signal Processing， 2017， 85： 512-529.

[20] Hoseinzadeh M S， Khadem S E， Sadooghi M S. Quantitative diagnosis for bearing faults by improving ensemble empirical mode decomposition[J]. ISA Transactions， 2018， 83： 261-275.

[21] Feng Z， Ma H， Zuo M J. Spectral negentropy based sidebands and demodulation analysis for planet bearing fault diagnosis[J]. Journal of Sound and Vibration， 2017， 410： 124-150.

作者簡介： 王朝阁（1992-），男，博士研究生。电话：18342236929;E-mail： dutwcg@163.com

通讯作者： 李宏坤（1984-），男，教授。电话：13084158910;E-mail： lihk@dlut.edu.cn