机械振源数估计的四线性平行因子方法研究
2021-08-09李志农朱亚静王冬
李志农 朱亚静 王冬

摘要: 针对三线性平行因子模型在机械振源数盲估计方法中存在的不足,即由于维度的限制只能对振动信号的部分信息建模,信号中的时间序列信息被忽略。将三线性平行因子的机械振源数估计方法扩展至四维,提出一种基于四线性平行因子的机械振源数估计方法。所提出的方法中,在三维的基础上增加了第四个维度(时间维),利用四线性交替最小二乘法迭代更新载荷矩阵,用核一致诊断法估计振源数。提出的方法既继承了三线性平行因子的独特优势,同时,又包含了更完整的振动信号的信息。相比三线性平行因子机械振源数估计方法,同组分数条件下四线性平行因子比三线性平行因子得到的核一致值更高,估计更加准确。仿真结果表明,提出的方法优于三线性平行因子机械振源数估计方法。实验结果进一步验证了提出的方法的有效性。
关键词: 故障诊断; 四线性平行因子; 盲源分离; 机械振源数估计; 四线性交替最小二乘
中图分类号: TH165+.3; TN911.7 文献标志码: A 文章编号: 1004-4523(2021)03-0619-07
DOI:10.16385/j.cnki.issn.1004-4523.2021.03.020
引 言
传统的机械故障源盲分离往往假设信号源数是已知的,例如,文献[1]提出的旋转机械监测预处理盲分离方法和文献[2]提出的用于壳体结构振源数目估计的独立分量分析方法,这些方法都是在信号源数已知的条件下进行盲分离。然而,在实际工程中,机械故障源数往往是未知的,为此,需要探讨关于源数未知条件下的机械故障盲分离方法。目前,基于源数估计的机械故障源盲分离方法取得了一些进展[3?6],例如,文献[3]结合分数傅里叶变换和盲分离理论的思想提出了一种机械故障源分离方法。文献[4]基于小波包分析思想提出了一种机械振动源数估计方法。然而,这些机械故障源数盲估计算法都属于二维数据处理方法,采用矩阵分解,并附加了一些约束条件。一般来说,矩陣分解不是唯一的,除非施加约束性条件,如正交性、Toeplitz和恒模特性等。但实际应用中并不能满足这些苛刻的约束条件,所以需要寻求新的方法解决这一问题。
近年来,平行因子模型(PARAFAC)[7?8]因具有分解唯一性的优势备受关注,它起源于平行比例分布原则,因其优势,平行因子理论在许多领域得到快速发展,例如化学分析领域[9]、无线通信领域[10]、环境化学计量领域[11]、故障诊断领域[12]。特别在信号处理和故障诊断领域内平行因子模型现已成为一种新型的、有力的研究手段。例如文献[13]将平行因子理论应用到阵列多参数的联合估计中。文献[14]将三维平行因子应用到机械振源数估计之中,该方法可有效估计机械振源数目。但是实际的应用中,使用现有的三维平行因子进行机械振源数估计时,只能对采集信号的传感器数目、振动信号的分段数以及每个数据段包含的数据点数信息进行建模,振动信号中的时间序列信息被完全忽略,振动信号包含的信息不完整,所以有必要将三维平行因子机械振源数估计方法扩展至四维。目前,平行因子三维至四维的扩展取得初步的进展[15?17]。例如,文献[15]提出一种基于四线性平行因子的雷达角度和频率联合估计算法。文献[16]提出一种应用于环境分析的交变加权剩余约束四次线性分解模型。这些文献都表明四线性平行因子分解不仅保持了三线性分解唯一性的优点,而且数据收敛更加平稳,所含的信息更加全面,更不容易陷入局部最优化。但是在机械振源数估计方面三维平行因子到四维平行因子的扩展还是空白的。
为此,针对现有的三线性平行因子在故障盲分离中存在的不足,本文将三维平行因子扩展至四维即引入(时间维)解决振动信号时序信息被忽略的问题,提出了一种基于四线性平行因子的机械振源数估计方法。它是在三维的基础上引入第四维(时间维)并将四线性平行因子盲分离方法和核一致检测相结合,利用四线性交替最小二乘进行更新拟合,并且得出了最佳组分数下的载荷矩阵,能够有效地估计振源数目。
1 四线性平行因子模型
四线性成分模型分解如图1所示。
其中,Xq为一个四维矩阵,将Xq分解为大小分别为的相关矩阵A,B,C,D。G为一个维数为,并且超对角元素为1,其他元素为0的四维核对角矩阵,G也是一个四维残差矩阵;Eq为四维残差矩阵。
四维矩阵的四线性成分模型标量形式通常可以表示为
四线性平行因子模型是基于四线性成分模型分解理论,采用四线性交替最小二乘理论得到模型的最优解。四线性平行因子模型将四维矩阵X铺展成二维矩阵形式,沿四个方向进行交替分解得到,其有如下四种不同的模型表述形式
式中 是对角化算子,表示选矩阵A的第i行作为新生成矩阵的主对角线元素,矩阵其余的位置均为零。其他对角化算子,,表示含义与表示的含义相似。
2 基于振源估计的四线性平行因子盲分离模型构建
对于N个源信号构成的信号向量集,它的线性瞬时混叠模型可以表示为
式中 A为L×N维的混合矩阵,为N个源信号残余向量集。为L维观测信号。假定一个时间段内每一个传感器采集M个数据点(共N个传感器),将传感器采集到的信号中心化处理,然后将进行中心化处理后的观测信号均分成不重叠的J个数据段,每一个数据段包含M/J个数据点记其为K,每一个数据段对应的采集时间为h,则共分为t/h个时间段记其为I。则线性混叠模式也可以表示为
3 振源数的估计
四维数据用四线性平行因子分析方法计算其最佳组分数时,用核一致诊断算法(CORCONDIA)[18]来预先估计正确的成分数来确定机械振动信号的振源数。核一致诊断法通过计算核一致值(core?consistency)来确定体系的成分数,其计算公式如下
式中 是模型的组分数;式(14)反映了不同组分数时理想情况下的核心阵与最小二乘拟合阵的拟合程度。为拟合阵G的元素;是超对角阵T的元素。T为平行因子模型中的超对角阵,它是在理想情况下取正确组分数时用Tucker3[19]方法得到的核心阵;G为用Tucker3方法得到的最小二乘拟合阵。一般认为核一致值为80%到100%模型有效,40%到80%之间的值表示模型可能有效,但有轻微的特异性或相关性,而低于40%的值意味着模型无效。
4 仿真研究
为验证提出的方法的有效性,在此,先进行仿真研究,仿真源信号如下
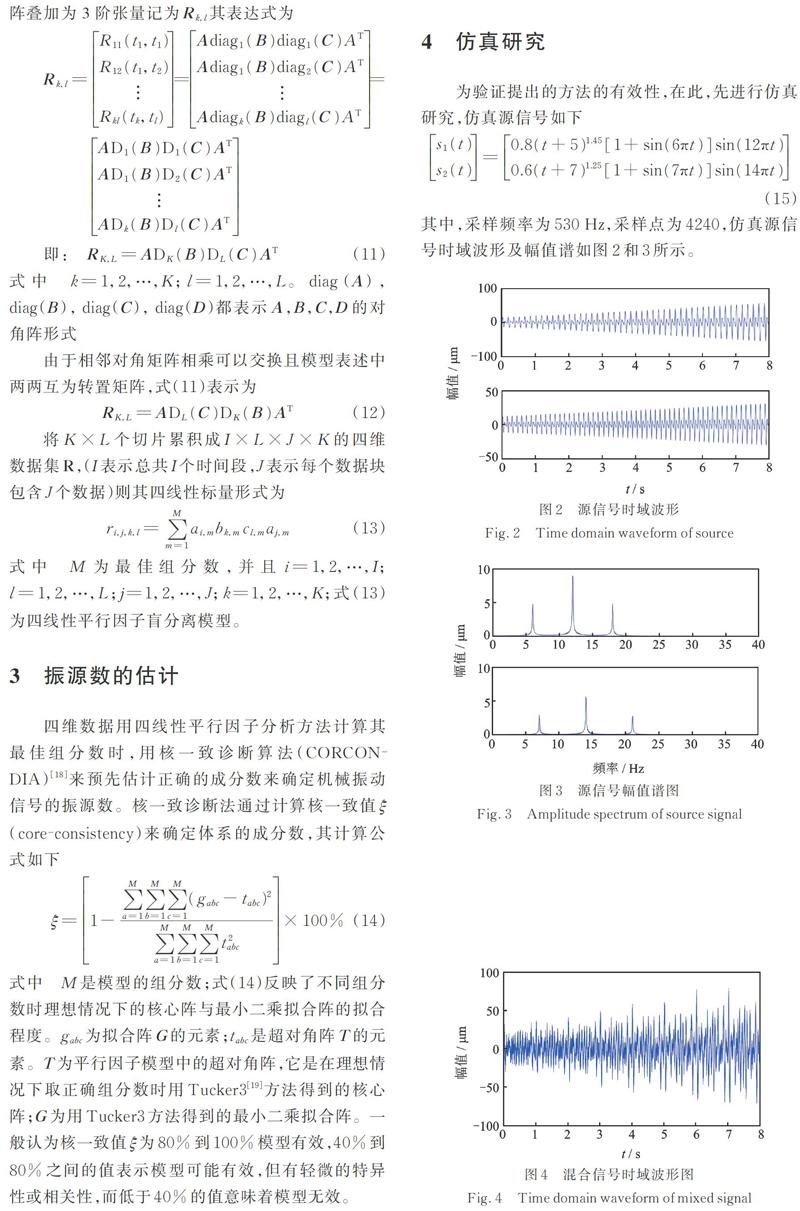
其中,采样频率为530 Hz,采样点为4240,仿真源信号时域波形及幅值谱如图2和3所示。
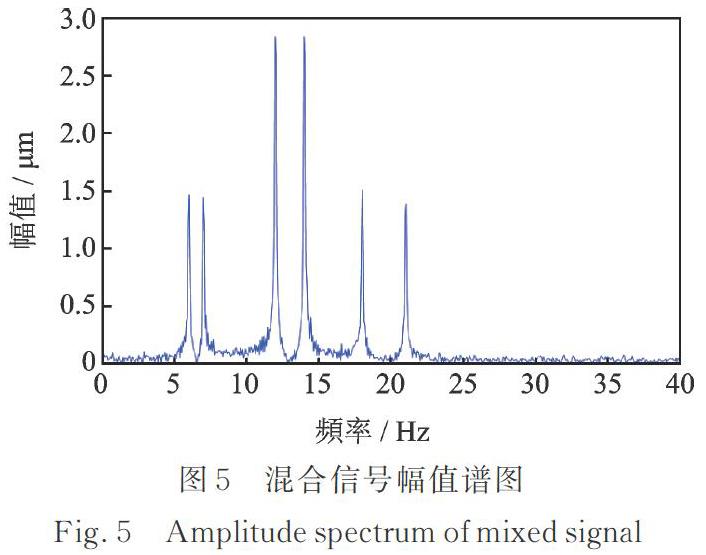
设置混合矩阵A为[0 1]区间的随机数,根据线性瞬时混叠模型得到虚拟观测信号。混叠后的虚拟观测信号的时域波形图和幅值谱图分别如图4和5所示。由图4和5可知,在混合信号时域波形图中无法辨识源信号特征频率,两个仿真信号的特征频率完全混叠在一起。
通过核一致检测算法估计最佳组分数(即振源数),使用四线性最小二乘法进行迭代,计算其核一致值、残差平方和与迭代次数,若核一致值大于80%,且残差平方和低于1000和迭代次数低于30000,算法有效(一般而言,残差平方和为每一次迭代残差平方的累加,当残差低于10-6并且不再减少时迭代结束)。
由图6可知,当组分数为2时,核一致值为100%,当组分数为3时,核一致值为0。核一致值在2时满足核一致检测的条件并且在之后发生突变,当组分数为2时,迭代次数低于30000,残差平方和小并且满足限制条件,说明最佳组分数值为2即振源数为2,算法有效。在组分数值为2时得到的4个分解载荷如图7所示,载荷矩阵B,D分解形式相同,符合式(12)中四线性平行因子盲分离模型。
为了体现本文方法的优越性,在此给出了三线性平行因子源数估计方法的结果,如图8所示。当组分数为2时,核一致值为65%,当组分数为3时,核一致值为0,即振源数为2。虽然核一致值为2时满足核一致检测的条件,但是其核一致值低于80%,表明模型可能有效,即不能够非常准确估计振源数目。而本文提出的方法在组分数为2时,核一致值为100%,组分数为3时,核一致值为0,表明模型有效,且能够非常准确地估计振源数目,而不是“可能”。这是因为四维平行因子振源数估计方法增加了振动信号中的时间序列信息,包含信息更全面,得到的源数估计值也更加可靠。对比三线性平行因子同组分数下的迭代次数,四线性迭代次数更少。对比同组分数下残差平方和,如表1所示,四线性平行因子的的残差平方和更小,相比于三线性平行因子,收敛更加平稳。
5 实验研究
为了进一步验证四线性平行因子机械振源数估计方法的有效性,在此,将提出的方法应用到机械设备滚动轴承故障源数估计中。实验设备由一个小电机,传感器,时间计数器,功率计等设备构成。电机负载为0,电机转速约1797 r/min,相应的转频为fr=29.17 Hz,采样频率为48000 Hz,用电火花加工技术,分别在轴承内圈和轴承外圈设置两个故障。在驱动端,轴承内圈设置0.1778 mm的点蚀故障,轴承外圈设置0.5334 mm的点蚀故障。加速度传感器安放在电机壳体上,用两个加速度传感器采集信号,采样点数为10240,获得2通道观测信号,采集到的观测信号时域波形如图9所示。
首先,将采集到的数据进行中心化处理,并将处理后的观测信号分成不重叠的16段数据块,相对应的时间段为16,每一个数据段包含256个数据点。其次,将各段信号块之间的时滞协方差叠加成3阶并计算其时滞协方差矩阵,然后将这个3阶张量在时间段上叠加为4阶,用核一致诊断算法估计最佳组分数(振源数),用四线性最小二乘法进行迭代,计算其残差平方和与迭代次数,得到的结果如图10所示。
由图10可知,当组分数为2时,迭代次数在合理的范围,残差平方和满足限制条件并且核一致值远大于80%,当组分数等于3时核一致值接近0。核一致值在组分数等于2时满足核一致检测的条件并且在组分数等于3时发生突变,所以最佳组分数为2,即振源为2。
6 结 论
针对三线性平行因子只能对振动信号的部分信息建模,信号中的时间序列信息被完全忽略的缺陷,本文提出一种基于四线性平行因子的机械振源数估计方法。该方法将三线性平行因子扩展到四线性,增加了振动信号时间序列信息,弥补了三线性建模时只能对部分信息建模的缺陷,使數据包含的信息更完整。用四线性交替最小二乘法拟合迭代,同组分数下四线性得到的残差平方和比三线性的更小,表明四线性平行因子相比于三线性收敛更加平稳。用核一致诊断算法得到该模型下的最佳组分数(振源数目),同组分数条件下四线性比三线性得到的核一致值更高,更符合核一致估计条件。相比于三线性得到的可能有效的估计结果,四线性平行因子的估计更加准确。最后利用仿真和实验验证了提出的方法的有效性。
参考文献:
[1] Gelle G, Colas M, Servière C. Blind source separation: A new pre-processing tool for rotating machines monitoring?[J]. IEEE Transactions on Instrumentation and Measurement, 2003, 52(3): 790-795.
[2] 成 玮,何正嘉,张周锁. 基于独立分量分析的壳体结构振源数目估计方法[J]. 机械工程学报, 2014,50(19): 73-79.
Cheng Wei, He Zhengjia, Zhang Zhousuo. Estimation method of vibration source number of shell structure based on independent component analysis[J]. Journal of Mechanical Engineering, 2014, 50(19): 73-79.
[3] 李志农, 吕亚平, 岳秀廷. 基于分数Fourier变换的机械故障源盲分离方法的研究[J]. 轴承, 2010,(6): 47-50.
Li Zhinong,Lü Yaping, Yue Xiuting. Research on blind separation of mechanical fault sources based on fractional Fourier transform [J]. Bearing,2010,(6): 47-50.
[4] 毋文峰, 陈小虎, 苏勋家, 等. 机械振动源数估计的小波方法[J]. 机械科学与技术, 2011, 30(10): 1679-1682.
Wu Wenfeng, Chen Xiaohu, Su Xunjia, et al. Wavelet method for estimating mechanical vibration sources[J]. Mechanical Science and Technology, 2011, 30(10): 1679-1682.
[5] 张洪渊,贾 鹏,史习智,等. 确定盲分离中未知信号源个数的奇异值分解法[J]. 上海交通大学学报,2001, 35(8): 1155-1158.
Zhang Hongyuan, Jia Peng, Shi Xizhi, et al. Singular value decomposition method for determining the number of unknown signal sources in blind separation[J]. Journal of Shanghai Jiao Tong University, 2001, 35(8): 1155-1158.
[6] LEl Huang, TEND Long, WU Shunjun. Source enumeration for high-resolution array processing using improved Gerschgorin radii without eigcn dccomposition[J]. IEEE Transactions on Signal Processing, 2008,56(12): 5916-5925.
[7] Harshman R A. Determination and Proof of Minimum Uniqueness Conditions for PARAFAC[J]. UCLA Working Papers in Phonetics, 1972, 22(1): 111-117.
[8] Carroll J D, Chang J J. Analysis of individual differences in multimensional scaling via an N-way generalization of “Eckart-Young” decomposition[J]. Psychometrika, 1970, 35(3): 283-319.
[9] Lee B M, Seo Y S, Hur J. Investigation of adsorptive fractionation of humic acid on graphene oxide using fluorescence EEM-PARAFAC[J].Water Research,2015, 73: 242-251.
[10] Zhang Xiaofei, Cao Renzheng, Zhou Ming. Noncircular-PARAFAC for 2D-DOA estimation of noncircular signals in arbitrarily spaced acoustic vector-sensor array subjected to unknown locations[J]. EURASIP Journal on Advances in Signal Processing, 2013: 107
[11] 张卉枫. 三维化学计量学方法应用于环境检测和药物分析[D]. 长沙:湖南大学, 2007.
Zhang Huifeng. Application of three-dimensional chemometrics in environmental detection and drug analysis [D]. Changsha: Hunan University, 2007.
[12] 杨 诚. 平行因子分析在多故障源盲分离中的应用研究[D]. 南昌:南昌航空大学, 2018.
Yang Cheng. Application of parallel factor analysis in blind separation of multiple fault sources[D]. Nanchang: Nanchang Hangkong University, 2018.
[13] 许凌云. 阵列多參数联合估计算法及应用的研究[D]. 南京:南京航空航天大学,2012.
Xu Lingyun. Research on the algorithm and application of array multi-parameter joint estimation [D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2012.
[14] 杨 诚, 李志农. 采用PARAFAC的欠定盲分离中机械振源数估计方法[J].华侨大学学报(自然科学版), 2018, 39(3): 337-342.
Yang Cheng, Li Zhinong. Using PARAFAC's method for estimating the number of mechanical vibration sources in underdetermined blind separation[J]. Journal of Overseas Chinese University (Natural Science Edition), 2018, 39(3): 337-342.
[15] 李建峰, 张小飞. 基于四线性分解的双基地MIMO雷达的角度和多普勒频率联合估计[J]. 航空学报, 2012, 33(8): 1474-1482.
Li Jianfeng, Zhang Xiaofei. Joint angle and Doppler frequency estimation of bistatic MIMO radar based on quadrilinear decomposition[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(8): 1474-1482.
[16] Liu Tingting, Zhang Ling, Wang Shutao, et al. Four-dimensional data coupled to alternating weighted residue constraint quadrilinear decomposition model applied to environmental analysis: Determination of polycyclic aromatic hydrocarbons[J]. Spectrochimica Acta Part A, Molecular and Biomolecular Spectroscopy, 2018,193: 507-517.
[17] Wang Z, Cai C, Wen F, et al. A quadrilinear decomposition method for direction estimation in bistatic MIMO radar[J]. IEEE Access, 2018, 6: 13766-13772.
[18] Bro R, Kiers H A. A new efficient method for determining the number of components in PARAFAC models[J]. Journal of Chemometrics, 2003, 17(5): 274-286.
[19] Tucker L. Some mathematical notes on three-mode factor analysis[J]. Psychometrika, 1966, 31: 279-311.
作者簡介: 李志农(1966-),男,教授。E-mail:lizhinong@tsinghua.org.cn
