基础激励下带金属外层的多黏弹性层纤维增强层合板的动力学模型
2021-08-09李晖荣万崇刘洋李小彭官忠伟
李晖 荣万崇 刘洋 李小彭 官忠伟
摘要: 以包含三层黏弹性材料、二层纤维增强材料和金属外层的多黏弹性层纤维增强(MVFLM)层合板为例,建立其在基础激励作用下的动力学模型。将坐标系设置在层合板结构的中心层,使用高阶剪切变形理论(考虑多个黏弹性层的剪切应变影响)和经典层合板理论分别对纤维层和金属层进行建模,进而获得MVFLM层合板的位移场函数;将基础激励等效成均布惯性力载荷,基于能量法获得系统的动能、势能和外力功,并利用正交多项式法表示边界条件对应的振型函数,成功求解具有多个黏弹性层的MVFLM层合板的固有频率、模态振型和振动响应;分别通过与已有计算结果进行对比以及实例测试,验证了所建立的动力学模型的有效性。
关键词: 动力学; 纤维增强层合板; 多黏弹性; 高阶剪切变形
中图分类号: TB301.2;TB334 文献标志码: A 文章编号: 1004-4523(2021)03-0610-09
DOI:10.16385/j.cnki.issn.1004-4523.2021.03.019
引 言
随着中国空军对高性能运输机、超音速战斗机、高速直升机等飞行器的加速列装以及动力装备的升级换代,带来了日益严峻的飞行器振动控制问题。带金属外层的多黏弹性层纤维增强 (multiple viscoelastic?layered fiber?reinforced laminate with outside metal?layers, MVFLM)复合材料是近年来出现的应用于航空航天结构上的一种新型的结构功能一体化材料[1?2],由高分子黏弹性层与纤维树脂层交替铺设,并与金属外层粘接而成,具有重量轻、减振降噪能力强、抗冲击性能好、抗疲劳性能突出、耐腐蚀、易于维修、成本较低等诸多优点,可在飞行器等武器装备的振动及噪声治理中发挥关键作用[3?4]。
目前,人們在关于带黏弹性层的纤维增强层合板动力学特性的研究中,基本都是将黏弹性材料作为芯层。通常采用外层材料的位移来表达黏弹性芯层位移,且绝大多数建模与分析研究都局限在三层层合结构上。例如,Nayak等[5]应用高阶剪切变形理论建立了以聚氯乙烯泡沫材料为核心的三明治板的理论模型,研究了材料性能、结构尺寸和自由、固支、悬臂等多种边界条件对固有频率特性的影响。Huang等[6]使用一阶剪切变形理论推导了该类型三明治层合板的振动方程,讨论了约束层厚度、黏弹性芯层厚度对固有频率和损耗因子的影响。Yang等[7]使用一阶剪切变形理论建立了带黏弹性芯层的三明治层合板的理论模型,研究了边界条件和纤维角度等参数对振动特性的影响。Cupia?和Nizio?[8]计算了带黏弹性芯层的纤维/树脂三层层合板在简支边界条件下的固有频率和损耗因子,发现在弹性层剪切模量升高时,理论模型在无量纲固有频率和损耗因子的计算上有一定的误差。Araújo等[9]在简支边界下对具有频率依赖性的三明治板(黏弹性材料为芯层)进行了解析建模,通过优化各层厚度,纤维角度等变量,在自由振动条件下获得了中心位移最小的最优化参数。Lu等[10]分析了单点简谐激励下该类型三明治板在简支边界下的共振与非共振响应,并与NASTRAN软件计算结果进行了对比,还分析了不同激励点对响应的影响。Arvin等[11]基于有限元方法,计算了单点简谐激励下该类型三明治梁的强迫振动。Wang等[12]应用哈密顿原理推导出了该类型三明治板的控制方程,分析了黏弹性芯层弹性模量对固有频率的影响,并得到了自由振动下水平和垂直方向的振动响应。
然而,人们针对MVFLM复合材料梁、板、壳结构的建模与分析研究较少。仅有Fujimoto等[13?14]测试获得了带有多个黏弹性夹层的纤维增强复合材料梁的自由衰减振动,并讨论了黏弹性材料不同排布位置对弹性模量和损耗因子的影响。试验表明,该类型结构具有较高的阻尼性能,多个黏弹性夹层可有效抑制拉伸载荷导致的材料失效,使极限荷载提高3%?15%。Fujimoto等[15]还研究了碳纤维增强三明治层合板(带聚乙烯基材料芯层)的阻尼特性,通过测试验证该类型层合板相对于传统纤维材料板的阻尼性能优势,其所在的科研团队[16]还对基于多层聚乙烯材料的碳纤维/树脂层合梁结构进行了静力学仿真与测试,并讨论了材料损耗因子的温度依赖性等问题。但上述研究缺乏建模分析过程与公式推导步骤,理论求解方式也含糊不清,且大部分集中在静力学和材料的力学参数求解上。另外,Castel等[17]使用高阶剪切变形理论建立了多层层合板结构的理论模型,但只用算例验证了该模型在三层夹心板固有频率计算上的有效性,并未对更复杂的多层结构进行建模和求解,也未关注振动响应问题。
通过上述文献调研可知,在分析带有多黏弹性层的纤维增强层合板结构的动力学问题时,建模中多采用纤维外层位移表达黏弹性芯层位移的方法,以达到减少未知数求解个数的目的。但该建模方法无法对三层以上的MVFLM层合板结构进行计算,建模的通用性不足,且并未考虑基础激励载荷的影响(实际工况下飞行器的复合材料蒙皮、地板、隔板等都可能受到基础激励载荷的作用)。为了解决上述问题,本文以包含三层黏弹性材料、二层纤维增强材料和金属外层的MVFLM层合板为例,建立其在基础激励作用下的动力学模型。最后,对中间层分别为二层和三层的黏弹性材料的两类MVFLM层合板进行实例研究,进而验证理论模型的有效性。
1 理论模型
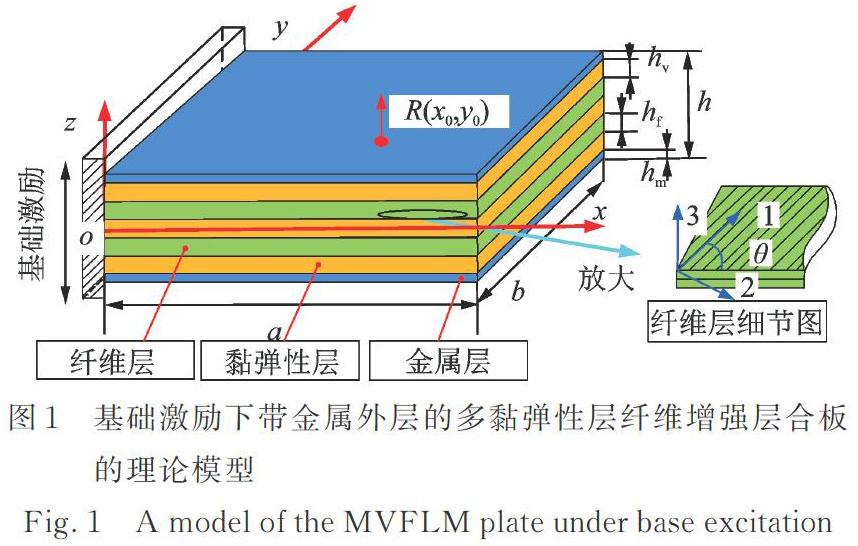
下面以包含三层黏弹性材料和二层纤维增强材料的MVFLM层合板为例,建立其在基础激励载荷作用下的动力学模型,如图1所示。
将黏弹性层中面作为参考平面,并建立坐标系xoy ,并在板厚方向设置坐标轴z,板长为a,板宽为b,板厚为h,其中金属层厚度为hm,黏弹性层厚度为hv,每个纤维层厚度均相同且为hf。该类型层合板受到基础激励载荷的作用,假设所关注的振动响应点为R(x0,y0)。另外,在纤维层中1代表纤维纵向,2代表纤维横向,3代表垂直于1?2平面的方向,且纤维方向与整体坐标系x轴的夹角为θ。
首先,根据高阶剪切变形理论,并考虑黏弹性层的剪切应变问题,将黏弹性层的位移场函数表示为[18]
式中 为高阶项系数,和分别为中面法线以x和y为轴向的偏转距离。
由于纤维层和金属层的yz和xz方向上的剪切应变可以忽略。MVFLM层合板中存在黏弹性层,所以不能忽略中面层位移的影响。另外,假设纤维层,金属层和黏弹性层结合紧密,则中面层位移,,可假设为同一个变量。所以纤维层和金属层位移场可以简化为
将已考虑x,y,yz,xz和xy方向影响的应力?应变表达式(6)和(7)代入(9)?(11)后,可分别获得MVFLM层合板弯曲振动时各层的动能和应变能。
式中 M和N为Ritz法求解时对应的截断系数,Amn,Bmn,Cmn,Dmn,Emn為待定Ritz参数,ω为角固有频率,Pm(ξ)和Pn(η)为正交特征多项式。其具体的表达式为
式中 Bk和Ck为系数参数,?(ξ)和φ(η)为确定边界条件的多项式函数,它们的表达式为
式中 W(ζ)为正交化过程中使用的加权函数,通常取1,而p,q,r,s的取值与层合板的边界条件有关,可根据自由、简支和固支不同的边界条件分别取值为0,1,2。对于图1中理论模型对应的悬臂边界条件,p=2,q=r=s=0。
将式(18)代入到式(12)中,并分别令cos(ωt)=1和sin(ωt)=1,可得含有待定Ritz参数的最大动能,最大势能和均布惯性力做功的最大值表达式为
根据参考文献[19],为保证足够的计算精度,通常M和N取8,则K,M分别为5(MN)阶方阵(即320阶)。特征向量q由五个子向量组成,即q={A B C D E},其中A=[A11 … Amn],m=1,2,…,M;n=1,2,…,N;B,C,D,E与A形式相同。若使式(23)有解,则q的系数矩阵行列式需为0。如此,利用式(23)便可求得层合板的固有频率和模态振型。再将计算获得的特征向量q代入公式(16)中,便可获得MVFLM层合板的各阶模态振型。
接下来,对层合板的阻尼矩阵C进行求解。假设可利用测试技术,首先获得模态阻尼比。由于比阻尼、模态损耗因子和之间有如下关系
则根据模态应变能法,可获得模态损耗因子与材料各个方向损耗因子的关系如下
式中 表示MVFLM板总的应变能,表示材料在各个方向上的应变能。
如此,可将材料损耗因子矩阵(为对角矩阵),表示为
根据耗散能的定义,将其表示为
式中 为MVFLM板的体积。
根据参考文献[20],通过对式(27)中的Ritz参数进行求导,可获得阻尼矩阵C。进一步,考虑基础激励载荷的影响,将式(14)和阻尼矩阵C代入到式(22)中,就可求得层合板的振动响应。由于通常实验获取的是绝对振动响应,其包括了结构自身的振动响应与基础激励位移之和。因此,可将基础激励下MVFLM层合板的振动响应表示为
2 实例研究
2.1 与文献结果对比
以文献[8]中所用的多层层合板为对象,使用本文的建模方法和求解公式,所获得的简支边界条件下的固有频率计算结果如表1所示,该层合板的长宽分别为a =304.8 mm,b=348.0 mm,纤维层厚度h1=h3=0.762 mm,黏弹性层厚度h2=0.254 mm,纤维层的弹性模量、剪切模量、泊松比和密度分别为E1=E3=68.9 GPa,黏弹性层的弹性模量、剪切模量、泊松比和密度分别为G2 =0.896 MPa。
通过对表1数据进行分析可知,本文与文献[8]获得的层合板前5阶固有频率偏差最大不超过6%,进而可初步证明本文模型及其计算方法的正确性。另外,需要说明的是,由于文献[8]只给出了三层层合结构的固有频率分析结果,本文为了方便对比,将第1部分建立的理论模型进行了退化处理,即在相同的层数下求解获得其固有频率。
2.2 实测结果对比
分别制备中间层为二层黏弹性材料和三层黏弹性材料的MVFLM层合板A和层合板B。其中,MVFLM层合板A的长、宽、厚尺寸分别,MVFLM层合板B的长、宽、厚尺寸分别270 mm×200 mm×2.35 mm各个金属外层厚度为0.3 mm,材料为钛合金,黏弹性层为0.5 mm,材料为ZN33,纤维层厚度为0.75 mm。
两种MVFLM层合板的铺层数量及铺设方式如表2所示。纤维层材料为TC500碳纤维/E21环氧树脂,铺设参数为,共有5层,每个铺层具有相同的厚度和纤维体积分数。纤维纵向弹性模量,纤维横向弹性模量,泊松比,剪切模量G12=G13=G23=4 GPa,密度。黏弹性层弹性模量,泊松比,剪切模量,密度。金属层弹性模量Em=108 GPa,剪切模量,泊松比,密度。
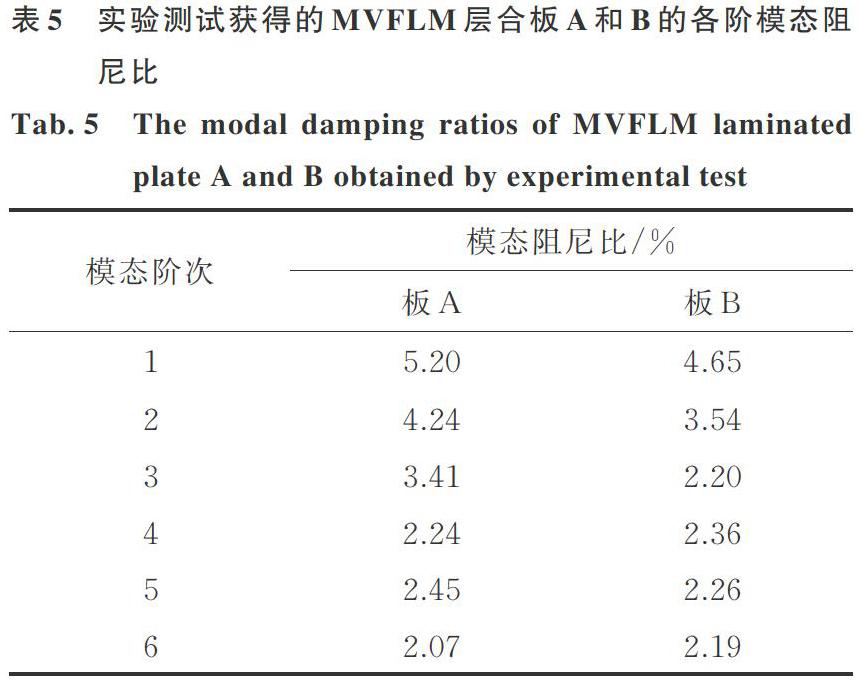
首先,在悬臂边界下进行实验,利用PCB 086C01模态力锤对两类MVFLM层合板进行模态测试,实验系统如图2所示,通过LMS采集分析仪分别记录脉冲激励信号和Polytec PDV?100激光测振仪获得的响应信号,再利用LMS Test.Lab 14A软件生成频响函数后,可利用PolyMax法辨识出悬臂边界下MVFLM层合板各阶模态参数,表3,4和5分别列出了测试获得的板A和板B的前6阶固有频率、模态振型和阻尼结果(为了节省篇幅,板B的振型未给出)。同时,为了方便比较,将利用Matlab程序计算获得的MVFLM层合板固有频率和振型结果也一并列入表3和4中。
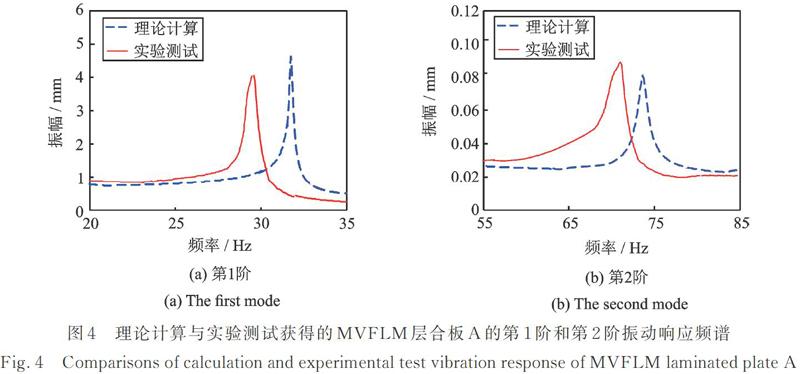
然后,搭建图3所示的实验系统来测试两类MVFLM层合板的振动响应。采用金盾EM?1000F电磁振动台对其进行基础激励,仍采用非接触激光测振仪获取响应信号(激光测点位置如图2所示)。实验时,需选取包含各阶固有频率的频率范围进行正弦扫频测试,在记录获得原始时域信号并经过分时段FFT变换操作后[21?22],可获得相应的频谱图。进一步,对频谱曲线峰值或指定的频率点(对应于非共振频率)进行辨识,可获得各阶共振响应和非共振响应结果。以获取第1阶和第2阶共振响应为例,图4给出了1g基础激励幅度下测试获得的频谱曲线。
最后,将在表5中通过测试获得的阻尼结果代入到分析模型中并生成阻尼矩阵,并在相同的激励幅度和响应测点位置,对两类MVFLM层合板的共振及非共振响应进行计算。表6和7给出了1g激励幅度下实验测试和理论计算获得的两类MVFLM层合板对应的共振及非共振响应结果,并给出理论与测试的误差。
通过对上述结果进行分析可知:(1) 利用该理论模型计算获得的MVFLM层合板A的固有频率最大误差为9.8%,层合板B的固有频率计算误差最大也不超过9.3%,且计算获得的模态振型形态与测试振型相一致,由此可知该模型在分析MVFLM层合板固有特性时具有较高的计算精度;(2) 计算获得的MVFLM层合板A的共振响应的最大误差为14.3% (板B最大误差12.5%),非共振响应的最大误差为14.3% (板B最大误差为14.9%)。由此可知,通过引入测试获得的模态阻尼比后,利用该模型计算获得的MVFLM层合板的共振及非共振响应也处于误差允许的范围内。这进一步验证了该理论模型的有效性,可以利用其实现对MVFLM层合板动力学参数的可靠预测和分析。
但仍有必要对上述误差的原因进行分析,其可能主要来自理论建模方面。由于在建模过程中忽略接触层的层间应力,纤维层的横向剪切应力、以及复合材料参数分散性的影响,并且由于理论模型中不同的材料层层数较多,导致模型简化后每一层细小的误差会产生累积。
3 结 论
本文采用理论与实验相结合的方法,对两种类型的MVFLM层合板的动力学参数进行了计算。通过与文献[8]计算获得的三层层合板固有结果进行对比后,发现结构的前5阶固有频率计算偏差最大不超过6%;通过与中间层分别为二层和三层黏弹性材料的MVFLM层合板的实际测试结果进行对比,发现两类层合板的固有频率最大误差不超过9.8%,共振及非线性响应的计算误差在7.7%?14.9%之间。上述计算分析误差都处于可接受的范围内,因而证明了本文所建立的动力学模型及其分析方法的有效性。
参考文献:
[1] 孟 光,瞿叶高.复合材料结构振动与声学[M].北京:国防工业出版社,2017:1-7.
Meng Guang, Qu Yegao. Vibration and Acoustics of Composite Structures[M]. Beijing: National Defense Industry Press, 2017: 1-7.
[2] 李 晖, 孙 伟, 许 卓, 等. 纤维增强复合薄板振动测试与分析方法[M]. 北京:机械工业出版社,2019:1-20.
Li Hui, Sun Wei, Xu Zhuo, et al. Vibration Test and Analysis Methods of Fiber-Reinforced Composite Thin Plates[M], Beijing: China Machine Press, 2019: 1-20.
[3] Treviso A, Van Genechten B, Mundo D, et al. Damping in composite materials: Properties and models[J]. Composites Part B: Engineering, 2015, 78: 144-152.
[4] 齊红宇, 温卫东, 崔海涛. 含孔复合材料层合板疲劳寿命预测研究[J]. 航空动力学报, 2003, 18(5): 658-661.
Qi Hongyu, Wen Weidong, Cui Haitao. Fatigue life predication of notched composite material laminates[J]. Journal of Aerospace Power, 2003, 18(5): 658-661.
[5] Nayak A K, Moy S S J, Shenoi R A. Free vibration analysis of composite sandwich plates based on Reddy's higher-order theory[J]. Composites Part B, 2002, 33(7): 505-519.
[6] Huang Z, Qin Z, Chu F. Vibration and damping characteristics of sandwich plates with viscoelastic core[J]. Journal of Vibration and Control, 2016, 22(7): 1876-1888.
[7] Yang C, Jin G, Ye X, et al. A modified Fourier-Ritz solution for vibration and damping analysis of sandwich plates with viscoelastic and functionally graded materials[J]. International Journal of Mechanical Sciences, 2016, 106: 1-18.
[8] Cupia? P, Nizio? J. Vibration and damping analysis of a three-layered composite plate with a viscoelastic mid-layer[J]. Journal of Sound & Vibration, 1995, 183(1): 99-114.
[9] Araújo A L, Soares C M M, Soares C A M, et al. Optimal design and parameter estimation of frequency dependent viscoelastic laminated sandwich composite plates[J]. Composite Structures, 2010, 92(9): 2321-2327.
[10] Lu Y P, Clemens J C, Roscoe A J. Vibrations of composite plate structures consisting of a constrained-layer damping sandwich with viscoelastic core[J]. Journal of Sound & Vibration, 1992, 158(3): 552-558.
[11] Arvin H, Sadighi M, Ohadi A R. A numerical study of free and forced vibration of composite sandwich beam with viscoelastic core[J]. Composite Structures, 2010, 92(4): 996-1008.
[12] Wang T, Sokolinsky V, Rajaram S, et al. Consistent higher-order free vibration analysis of composite sandwich plates[J]. Composite Structures, 2008, 82(4): 609-621.
[13] Fujimoto J, Tamura T, Ugo R. Dynamic mechanical properties for CFRP/damping-material laminates[C]. INTER-NOISE and NOISE-CON Congress and Conference Proceedings. Institute of Noise Control Engineering, 1991, 1991(4): 735-738.
[14] Fujimoto J, Tamura T, Todome K, et al. Mechanical properties for CFRP/damping-material laminates[J]. Journal of Reinforced Plastics and Composites, 1993, 12(7): 738-751.
[15] Fujimoto J, Tamura T. Development of CFRP/damping-material laminates[J]. Advanced Composite Materials, 1998, 7(4): 365-376.
[16] Tanimoto T, Fujimoto J, Tamura T, et al. Static and fatigue properties of CFRP/damping-material laminates[C]. 32nd Structures, Structural Dynamics, and Materials Conference, Baltimore, USA, 1991.
[17] Castel A, Loredo A, El Hafidi A. A comparison between models for the study of static and dynamic behavior of heterogeneous multilayer composite plates[J]. 2013: hal-00849758f.
[18] Meiche N E, Tounsi A, Ziane N, et al. A new hyperbolic shear deformation theory for buckling and vibration of functionally graded sandwich plate[J]. International Journal of Mechanical Sciences, 2011, 53(4): 237-247.
[19] Mahi A, Bedia E A A, Tounsi A. A new hyperbolic shear deformation theory for bending and free vibration analysis of isotropic, functionally graded, sandwich and laminated composite plates[J]. Applied Mathematical Modelling, 2015, 39(9): 2489-2508.
[20] Li H, Niu Y, Mu C, et al. Identification of loss factor of fiber-reinforced composite based on complex modulus method[J]. Shock and Vibration, 2017: 6395739.
[21] Li H, Wu H S, Zhang T N, et al. A nonlinear dynamic model of fiber-reinforced composite thin plate with temperature dependence in thermal environment[J]. Composites Part B: Engineering, 2019, 162: 206-218.
[22] Li H, Lü H Y, Sun H, et al. Nonlinear vibrations of fiber-reinforced composite cylindrical shells with bolt loosening boundary conditions[J]. Journal of Sound and Vibration, 2021, 496: 115935.
作者簡介: 李 晖(1982-),男,博士,博士后,副教授。电话:13709850965;E-mail:lh200300206@163.com
