钝体摆动间接激励式压电风力发电机的研究
2021-08-09阚君武廖卫林林仕杰张忠华黄鑫文一杰王淑云
阚君武 廖卫林 林仕杰 张忠华 黄鑫 文一杰 王淑云
摘要: 为满足风场环境中传感监测系统的自供电需求,提出一种钝体摆动间接激励式压电风力发电机,利用圆柱形钝体涡激振动产生的往复摇摆带动磁铁间接激励密封腔内压电换能器振动发电。介绍了发电机结构及工作原理,并进行了理论和试验研究,证明了其结构和原理的可行性。研究结果表明:其他条件确定时,输出电压随柔性梁长度和换能器质量增加以及耦合器的质量降低而增加,锁频带宽随柔性梁长度增加以及耦合器和换能器的质量降低而增加;此外,存在最佳负载电阻使输出功率达到最大。
关键词: 压电; 风力发电机; 涡激振动; 间接激励; 风场环境
中图分类号: TN384; TK83 文献标志码: A 文章编号: 1004-4523(2021)03-0577-07
DOI:10.16385/j.cnki.issn.1004-4523.2021.03.015
引 言
近年来,为满足风场环境中传感监测系统的自供电需求,避免使用化学电池造成环境污染,基于压电机理的俘能技术已成为国内外学者的研究热点[1?3]。当前,壓电发电机已广泛应用于回收自然环境中流体能[4?5]、旋转动能[6]、振动能[7]、人体运动能[8]等能量,其中,流体能作为绿色清洁能源的代表之一,回收利用价值显著。
在流体能量收集方面,压电式发电机相较于电磁式、静电式等俘能器具有结构简单、高功率密度/转换效率、易于实现微小化与集成化等优点[9]。现有的压电风力发电机大致可归为三类:①风车式[10],通过叶轮获取流体能,再由钢球、拨盘等部件激励压电振子振动发电,结构复杂、可靠性较低,仅用于流体黏度/流速低、使用空间不受限的场合;②谐振腔式[11],利用高速气流冲击谐振腔后经谐振腔放大的激振力激励压电振子振动发电,常用于超高流速场合能量收集,但对谐振腔长度要求高、流速适应性较差;③流致振动式[12],利用气流流经钝体产生的涡激升力驱动压电振子弯曲发电,结构简单、流速适应性强,适用于流速变化大的环境。
现有的流致振动式压电风力发电机,主要有涡激振动式、驰振式与颤振式等。其中,驰振式发电机与颤振式发电机多采用梁式压电振子结构,以弛振与颤振方式激励压电振子振动发电,因而存在可靠性低、稳定性较差等问题[13]。涡激振动式压电风力发电机通过气流流经钝体后所生成的旋涡迫使钝体后方的压电振子弯曲发电[14],或利用气流流经钝体时产生的周期性升力驱动连接有悬臂梁式压电振子的钝体沿垂直气流方向往复摆动[15?16]以带动压电振子弯曲变形发电。此类发电机在工作时存在“锁频”现象[16](当脱涡频率fω与系统固有频率fn相近时,钝体将产生共振现象,振幅突然增大,压电振子发电量较大),可有效提高发电机的能量收集效率,因此具有重要的研究价值。现有的涡激振动式风力发电机虽不断完善,但仍存在发电能力及环境适应性较差(仅在很窄的风速范围内有效工作)、可靠性低(压电振子与气体直接耦合时冲击较大且易变形过大而损坏)等缺陷。
为改善涡激振动式风力发电机在环境适应性、可靠性、发电能力等方面的不足,提出一种钝体摆动间接激励式压电风力发电机以满足复杂风场环境中传感监测系统的自供电需求。利用圆柱形钝体与风场耦合作用产生涡激振动,并通过磁铁间接激励密封腔内的压电振子振动发电,具有可靠性高(压电振子置于密封腔内,有利于将脆弱关键部件密封,避免风速过大时压电振子与气流直接耦合损坏压电振子,提升了发电机在恶劣气候环境中的适应性)、发电能力与环境适应性强(可通过改变发电机的结构参数,调节发电机的输出特性)等优点。
1 风力发电机的结构及工作原理
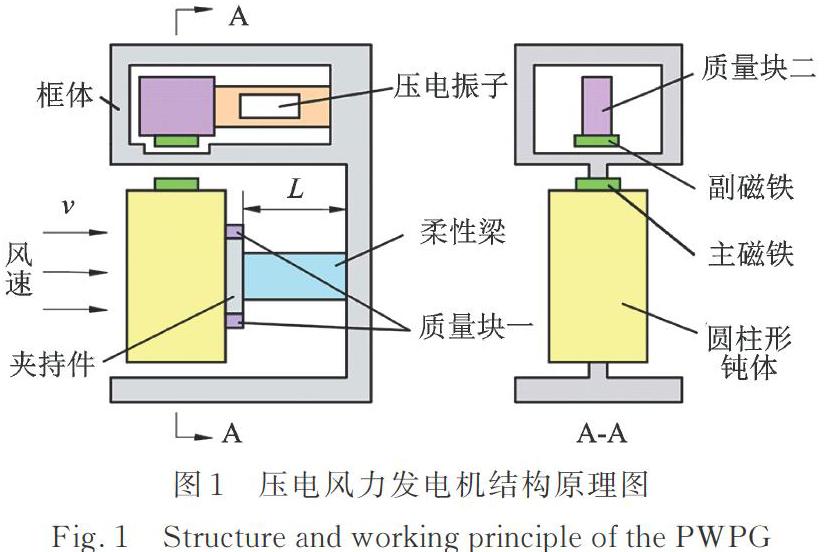
本文提出的钝体摆动间接激励式压电风力发电机具体结构如图1所示。柔性梁一端固定在框架,自由端通过夹持件安装有圆柱形钝体,其中夹持件上下两端对称安装有质量块一,圆柱形钝体上端固定有主磁铁;压电振子一端安装有质量块二及副磁铁,且副磁铁与主磁铁正对安装、相互吸引,另一端固定在密封腔内壁上。工作时,压电风力发电机通过摆动的钝体和磁铁间接激励压电振子,避免了气流直接冲击压电振子,具有可靠性高、流速适应性强等优点。
图2为圆柱形钝体摆动时流场的脱涡尾迹图。根据流体动力学理论,气流流经钝体后将在其背流面形成卡门涡街(图2所示),涡街脱落时钝体将受到y向的升力FL。由于连接钝体的柔性梁一端固定,因此钝体将产生y向弧形摆动,并通过主、副磁铁间的吸引力间接激励压电振子振动发电,实现了流体能到电能的非接触式转换。
现有研究表明,可将周期性升力FL作为钝体摆动时的主要激振力,忽略阻力对y向振动的影响,其中,升力FL与升力系数CL可表示为[16]:
式中 ρ为空气密度,为圆柱体迎风面的特征尺寸,D和H分别为钝体直径和长度,v为风速。
由于圆柱形钝体产生“锁频”现象时钝体振幅较大,且发电机具有较好的发电性能。因此,若能够通过参数匹配降低系统固有频率fn,使其在较低脱涡频率fω(即低风速)下出现“锁频”现象,将有助于改善发电机的输出性能。脱涡频率fω与系统固有频率fn的表达式为:[17]
式中 St为与雷诺数Re相关的Strouhal数,雷诺数Re=v·D/(为运动黏度),其对升力FL及Strouhal数St都有较大的影响,K与M分别为系统等效刚度与等效质量。由此可见,通过改变v,K,M可调节脱涡频率与系统固有频率,该措施有望实现系统固有频率与脱涡频率相匹配,从而达到锁频目的。
2 发电机的激励与响应特性分析
以往研究表明,压电振子的发电能力主要由结构尺寸及其动态响应所决定,生成的电压、单位时间内产生的电能及最大输出功率可表示为[18]:
式中 η为与压电振子结构尺度及材料参数有关的系数;K2,Fcy,y2分别为压电振子等效刚度、所受的磁力和变形量;s=2πfω=2πSt·v/D为涡激圆频率,Cf为自由电容。上述公式表明,当其他参数确定时,可通过提高压电振子变形量与振动频率提高发电能力。
虽然涡激振动式压电流体发电机已有较多的理论及试验成果可借鉴,但是本文提出的风力发电机中压电振子与流体不直接耦合(钝体由升力激励,通过主副磁铁间的相互作用力实现间接激励压电振子振动发电),此类发电机的有关动态响应及发电特性未有报道,故首先需要从理论上研究发电机的响应特性。为便于分析,仅考虑发电机在y方向振动位移量,并对振动过程做了相应假设(如:假设压电振子是小变形弹性基,符合欧拉?伯努利梁的假设条件等)。根据机械振动和流体动力学知识,可将该发电机简化为以磁力Fcy相关联的两自由度弹簧?阻尼?质量系统(如图3所示)。其中,耦合器系统由柔性梁、质量块一、夹持件、主磁铁及圆柱形钝体构成,换能器系统由压电振子、质量块二及副磁铁构成。因此,发电机的振动微分方程为
式中 y1(t)为圆柱体y向振动位移量;M1和M2分别为等效耦合器质量和等效换能器质量;C1=c0+c1为耦合器系统等效阻尼,co为系统结构阻尼,c1为气流附加阻尼;C2=c2+cpp为换能器系统等效阻尼,c2和cpp分别为结构阻尼和压电阻尼;K1及K2分别为耦合器及换能器系统的等效刚度;压电振子等效机电耦合系数为=[(oc2+nsc2)M2Cf ];R为负载电阻,Vg为负载电阻两端电压;Fcy为主副磁铁间在y方向上的切向磁力,其大小与主副磁铁间距、正对面积及磁铁自身参数有关,在振动过程中随时间变化。由于磁铁间非线性要素繁多,且尚无准确切向磁力计算公式可借鉴,故难以通过计算公式表征切向磁力Fcy的大小。鉴于此,本文通过建立磁极模型对切向磁力进行仿真计算,结果如图4所示。
在图4中,θ为主副磁铁所连接柔性梁与压电梁在摆动过程中存在的偏差角。仿真获取了-20°<θ<20°范围内切向磁力Fcy的大小(实际范围约-10°<θ<10°)。由图可知,磁力Fcy与θ角间具有很强的非线性与波动性,磁力Fcy有效值大体上随θ角的增大先增后减。磁力在发电机中主要起连接耦合器与换能器的作用,在后续测试中将选取合适尺寸磁铁以保证工作时换能器与耦合器不发生脱离。
综上,可见风速v(影响脱涡频率)、柔性梁长度L(影响等效刚度,进而改变系统固有频率)、耦合器质量M1及换能器质量M2(影响等效质量,进而改变系统固有频率)等因素均对风力发电机的性能有较大影响。然而,由于实际风场分布较为复杂,且难以获取CL,Fcy及c1等关键参数精确值求解动力学方程,因此下文将通过试验分析的方法研究上述结构参数与风速对发电机输出性能的影响规律。
3 试验测试与分析
在现有研究资料中,康庄等 [19]对采用不同质量比γ*钝体的压电发电机进行了初步探究,其研究结果表明:发电机采用高质量比(γ*=13)圆柱体时输出电压到达最大值后与以往发电机电压输出特性有很大不同,其不随风速的进一步增大而迅速降低,而是在一定风速范围内保持稳定,且稳定输出电压对应的风速带较宽,其中质量比γ*定义为
式中 分别为钝体质量及钝体振动时位移流体质量。王艺等 [20]指出,采用高质量比钝体(γ*>10)的压电发电机在振动初期便可认为已进入锁频状态,振动特性较好。
为利用高质量比钝体这一特性,试验选取了合适的高质量比钝体参数并确定了待研究参数的试验范围。用于探究试验参数对输出电压与输出功率影响规律的发电机样机及测试系统如图5所示,试验的相关参数如表1所示,其中,压电振子基板为经热处理的铍青铜,压电陶瓷材料为PZT?4。試验所用仪器设备包括鼓风机(额定转速2800 r/min)、变频器(变频范围0?50 Hz)、DS5042M型数字存储示波器、风速仪、可调电阻器、整流电路等。试验中通过调节变频器频率ft改变风速v大小(二者线性关系良好),变频器步长1.0 Hz,实际风速范围为0?24 m/s。此外,将压电振子所产生电压的最大值作为输出电压值Vg。
在试验中,为获得压电风力发电机在风场中的振动情况,利用示波器截取输出电压Vg时域波形图并利用Matlab对输出电压Vg进行了FFT分析,获得了图6所示幅频特性曲线,进而汇总得到压电振子振动频率与风速的关系曲线(以改变柔性梁长度为例),如图7所示。
由图6可见,电压波形峰值并非理想的正弦波,含有随机振动成分,存在一个振动主频f及多个振动次频相叠加的现象,可根据输出电压变化情况反映发电机振动情况。由图7可知,采用高质量比钝体时发电机在低风速下便直接进入锁频状态,保证了发电机有良好的振动特性。下文将进一步分析结构参数与风速对发电机输出电压/功率的影响。
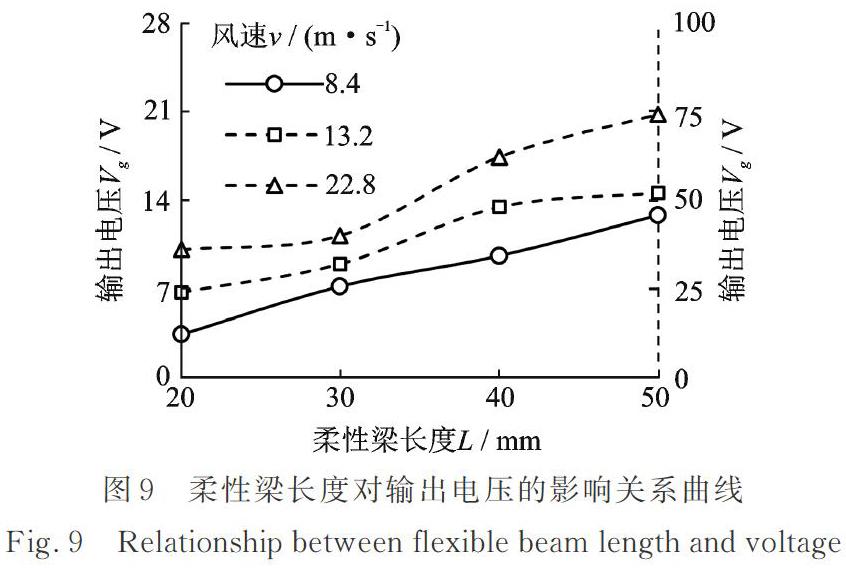
图8为柔性梁长度L不同时输出电压Vg与风速v的关系曲线。由图可知,在不同梁长下输出电压均随风速的增大先增大后趋于平缓:当v≤13.2 m/s时Vg随v增大而增大,且增速逐渐加快;当v≥13.2 m/s后,Vg的增速较为平缓。此外,当L≤30 mm时,Vg较为稳定且有轻微下降趋势;当L>30 mm后,Vg变化较平稳且仍呈现上升趋势。此外,由图8可知锁频带宽随柔性梁长度的增大而增加。另一方面,由图9柔性梁长度L对输出电压Vg的影响关系曲线可知,柔性梁长度对输出电压影响显著:相同风速下,L越长,Vg越大。产生上述现象的原因在于:风速较低时,升力随风速增大而增大,柔性梁长度越长系统刚度值越小,钝体越容易起振且振幅增大;风速较高时,因非线性流固耦合作用力及磁铁间磁力的耦合作用,压电风力发电机振幅将趋于稳定。综上,可通过改变柔性梁长度调节发电机输出电压及锁频带宽。
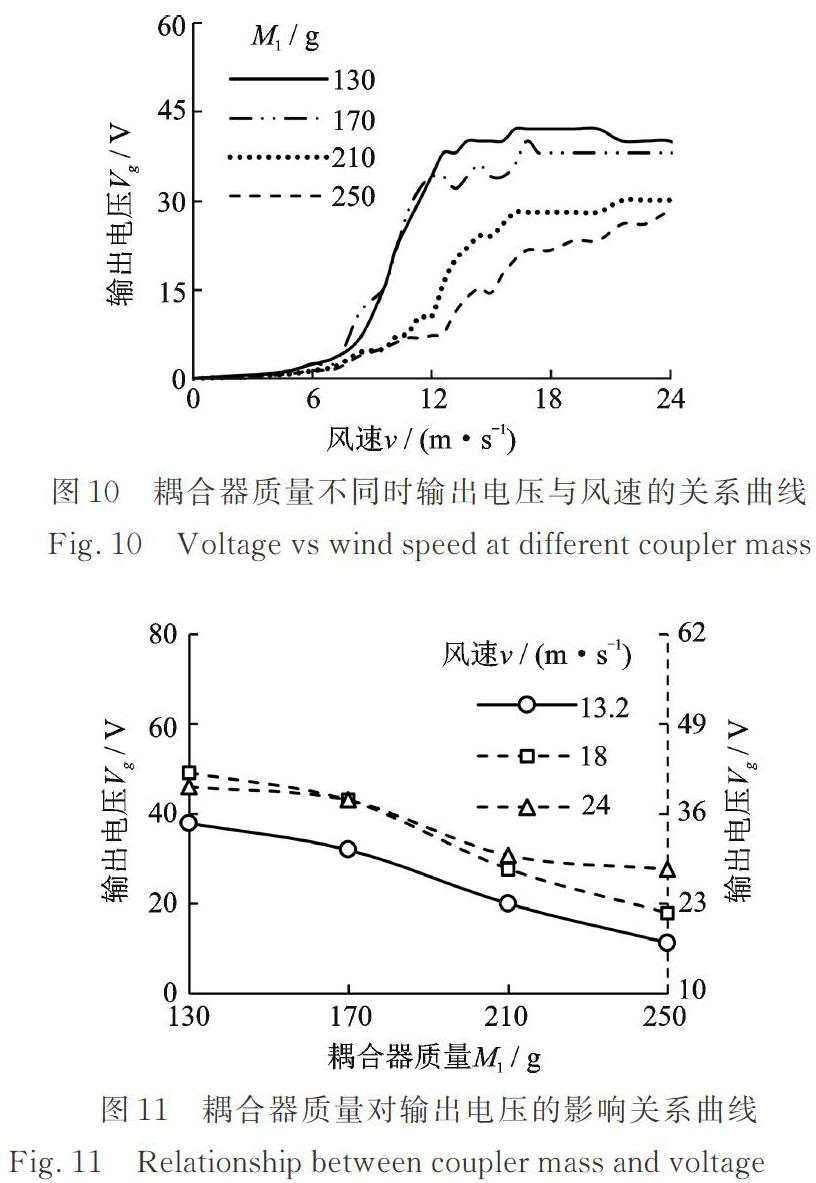
图10为耦合器质量M1不同时输出电压Vg与风速v的关系曲线。据图可知,耦合器质量对发电机的输出电压有较大影响,且锁频带宽随耦合器质量的增大而变窄。当M1≤170 g时,输出电压Vg随风速v先增大后趋于平缓;当M1>170 g后,Vg增速随v的增大而增大,其增速先急后缓且仍呈现上升趋势。由图11耦合器质量M1对输出电压Vg的影响关系曲线可知,风速v(v>13.2 m/s)相同时,输出电压Vg随耦合器质量M1的增大而近线性减小。产生上述现象的原因在于增加耦合器质量M1后,钝体达到一定振幅时所需升力及风速均增大。通过上述分析易知,可通过降低耦合器质量提升/拓宽发电机电压输出性能/锁频带宽,且增加耦合器质量可降低高风速下的振幅,提升安全性及可靠性。
图12为换能器质量M2不同时输出电压Vg与风速v的关系曲线。由图可知,增大换能器质量可在高风速(v≥21 m/s)时提升发电机输出电压,但相应的锁频带宽会降低。当v≤12 m/s时,不同M2对应的Vg值相差不大;在12 m/s 至此,已分析并获得了柔性梁长度L、耦合器质量M1及换能器质量M2对压电风力发电机电压输出特性的影响规律。为进一步探究上述结构参数对发电机输出功率的影响规律,下文对风速24 m/s时的三种不同参数组合(A [L=30 mm,M1=130 g,M2=50 g],B [L=50 mm,M1=90 g,M2=10 g],C [L=30 mm,M1=130 g,M2=10 g])进行功率试验。 图14为风速不同时发电机输出功率P与负载电阻R的关系曲线。从图中可知,经整流后,输出功率随负载电阻的增大而先增后减,即存在最佳负载Ropt使输出功率最大。此外,当负载一定时,风速对发电机输出功率影响显著。在最佳负载电阻Ropt=1000 kΩ及风速为22.8 m/s时,发电机输出功率达到最大值4.84 mW。最佳负载电阻是由于压电陶瓷内阻和外部电阻的不同匹配特性决定的。 4 结 论 为改善现有压电风力发电机在环境适应性、可靠性、发电能力等方面的不足,提出了一种钝体摆动间接激励式压电风力发电机。从理论和试验两方面研究了柔性梁长度、耦合器质量、换能器质量及风速对发电机输出电压、锁频带宽及输出功率的影响规律,并得到了以下结论: (1)输出电压随风速的增大而先增大后趋于平缓;风速较低时,输出电压随风速增大而增大,且增速较缓;当风速升高时,输出电压将迅速增大至最佳输出电压值,此后输出电压保持稳定。由此可见,该发电机可在较大风速范围内输出较高电压,即发电机锁频带宽较宽、发电性能较好; (2)柔性梁長度、换能器质量与耦合器质量对发电机的发电特性及锁频带宽有较大影响,采用以下措施可有效提高发电机的发电能力:风速较低时(v≤13.2 m/s),增加柔性梁长度可提升输出电压;较高风速时(13.2 m/s (3)在任一风速下,发电机的输出功率均随负载电阻的增大而先增压减,存在最佳负载1000 kΩ使发电机输出功率最大。当风速为22.8 m/s时,最大输出功率达4.84 mW。 本文证明了钝体摆动间接激励式压电风力发电机原理的可行性,为满足风场环境中传感监测系统的自供电需求提供了一种可行的方法。 参考文献: [1] 王光庆, 崔素娟, 武海强, 等.多稳态压电振动能量采集器的动力学模型及其特性分析[J].振动工程学报,2019,32(2):252-263. Wang G, Cui S, Wu H, et al. Dynamical model and characteristics of a multi-stable piezoelectric vibration energy harvester[J]. Journal of Vibration Engineering, 2019, 32(2): 252-263. [2] Zhang Z, Wang S, Kan J, et al. A pneumatic piezoelectric vibration energy harvester based on the compressed air-transducer-structure interaction[J]. Energy Conversion & Management, 2020, 213: 112861. [3] 阚君武, 文欢, 王淑云,等. 磁铁夹持式压电俘能器输出性能分析与试验[J].振动工程学报, 2019, 32(1):80-86. Kan J, Wen H, Wang S, et al. Performance analysis and test of a piezoelectric energy harvester based on magnets holding[J]. Journal of Vibration Engineering, 2019, 32(1):80-86. [4] Kan J, Fan C, Wang S, et al. Study on a piezo-windmill for energy harvesting?[J]. Renewable Energy, 2016, 97: 210?217. [5] Bibo A, Daqaq M F. Energy harvesting under combined aerodynamic and base excitations[J]. Journal of Sound and Vibration, 2013, 332(20):5086-5102. [6] Kan J, Fu J, Wang S, et al. Study on a piezo-disk energy harvester excited by rotary magnets?[J]. Energy 2017, 122: 62?69. [7] Fan K, Chang J, Chao F, et al. Design and development of a multipurpose piezoelectric energy harvester[J]. Energy Conversion & Management, 2015, 96:430-439. [8] Fan K, Liu Z, Liu H, et al. Scavenging energy from human walking through a shoe-mounted piezoelectric harvester[J]. Applied Physics Letters, 2017, 110(14):143902. [9] Hobbs W, Hu D. Tree-inspired piezoelectric energy harvesting[J]. Journal of Fluids & Structures, 2012, 28(1):103-114. [10] Yang Y, Shen Q, Jin J, et al. Rotational piezoelectric wind energy harvesting using impact-induced resonance[J]. Applied Physics Letters, 2014, 105(5):053901. [11] Zou H, Chen H, Zhu X. Piezoelectric energy harvesting from vibrations induced by jet-resonator system[J]. Mechatronics, 2015, 26: 29-35. [12] Wang J, Geng L, Ding L, et al. The state-of-the-art review on energy harvesting from flow-induced vibrations[J]. Applied Energy, 2020, 267: 114902. [13] Yang Y, Zhao L, Tang L. Comparative study of tip cross-sections for efficient galloping energy harvesting[J]. Applied Physics Letters, 2013, 102(6):064105. [14] Song R, Shan X, Lü F, et al. A study of vortex-induced energy harvesting from water using PZT piezoelectric cantilever with cylindrical extension[J]. Ceramics International, 2015, 41:S768-S773. [15] Dai H, Abdelkefi A, Yang Y, et al. Orientation of bluff body for designing efficient energy harvesters from vortex-induced vibrations?[J]. Applied Physics Letters, 2016, 108(5):053902. [16] 王淑云, 严梦加, 阚君武, 等. 间接激励式压电风力俘能器[J]. 光学精密工程, 2019,(5):1121-1127. Wang S,Yan M,Kan J,et al. Study of piezoelectric wind energy harvester with indirect excitation[J]. Optics and Precision Engineering, 2019,(5):1121-1127. [17] Liu F, Zou H, Zhang W, et al. Y-type three-blade bluff body for wind energy harvesting?[J]. Applied Physics Letters, 2018,112:233903. [18] 王淑云, 富佳伟, 阚君武, 等.一种脱涡纵振式压电管道气流发电机[J]. 机械工程学报, 2019, 55(8): 24-29. Wang S, Fu J, Kan J, et al. A pipe airflows piezoelec- tric energy harvester with longitudinal vibration excited by vortex shedding[J]. Journal of Mechanical Engineering, 2019, 55(8): 24-29. [19] 康莊, 张橙. 雷诺数对圆柱体涡激振动特性影响研究[J]. 华中科技大学学报(自然科学版), 2017,45(11):79-84. Kang Z,Zhang C. Impact of Reynolds number on vortex-induced vibration performance of cylinder[J]. J. Huazhong University of Science & Technology (Natural Science Edition) , 2017,45(11):79-84. [20] 王艺, 陈伟民, 林缅. 锁频阶段涡激振动圆柱的附加质量研究[C]. 2006年度海洋工程学术会议,南宁,中国,2006. Wang Y, Chen W, Lin M. Study on additional quality of vortex-induced vibrating cylinder in frequency-locked phase[C]. Ocean Engineering Conference, Nanning, China, 2006. 作者简介: 阚君武(1965-),男,教授,博士生导师。电话:(0579)82286598; E-mail: jutkjw@163.com 通讯作者: 张忠华(1980-),男,教授,硕士生导师。E-mail: zhangzhh@zjnu.cn
