一种非线性宽频压电能量收集系统的动力学特性分析

刘久周 张凤玲 辛健强 王润 董永朋 屈强

摘要： 提出了一种基于同步开关电路的非线性宽频压电能量收集器，并利用高阶谐波平衡法对能量收集系统的频域响应、能量输出功率及其影响因素等内容展开了理论研究，同时利用Hill法对系统的稳定性进行了分析。研究结果表明在基于同步开关电路的能量收集系统中引入副梁，可以大大拓宽能量收集系统工作频带;适当减小同步开关电路的电容比，虽然会降低能量收集系统在共振峰附近的能量收集能力，但可以拓宽系统的工作带宽;能量收集系统的工作带宽随副梁与质量块间初始间隙的减小以及副梁刚度的增大而拓宽，可根据振动能量源频率带宽及能量的频域分布规律，对系统关键参数进行匹配设计，以获得更好的能量收集效果。

关键词： 振动能量收集; 非线性; 同步开关电路; 高阶谐波平衡法; 动力学特性

中图分类号： TN712+.5; O322    文献标志码： A    文章编号： 1004-4523（2021）03-0567-10

DOI：10.16385/j.cnki.issn.1004-4523.2021.03.014

引  言

压电能量收集系统以压电材料作为媒介，将系统中结构振动的机械能转化为电能，进而通过外接能量收集电路将产生的电能收集起来。收集的能量可以为系统内的电子元件供能，降低系统对电源的需求，因此压电能量收集系统在机械、电子等领域具有广阔的应用前景，受到了研究人员的广泛关注[1]。

早期的被动线性压电能量收集系统，存在能量收集效率低、工作带宽较窄、对振动环境变化敏感等缺陷[2?3]。针对被动线性压电能量收集系統的缺陷，近年来以同步开关电路为代表的半主动能量收集电路成为研究人员关注的热点。基于压电材料的同步开关能量收集（Synchronized Switch Harvesting， SSH）技术是一种典型的半主动压电能量收集技术，最早由Richard等提出[4]。其工作原理为：在粘贴于结构上的压电片两电极之间连接有同步开关电路，压电片随结构的振动发生弹性形变，当压电片电极电压达到极值时，电路中的同步开关元件自动迅速闭合，电极电压方向发生“翻转”，然后开关又迅速断开，这使得压电片电极之间始终保持较高的电压水平，进而使其收集能力相对于被动的压电能量收集系统得到大大提升。

目前应用最广泛的同步开关能量收集器是基于电感元件的同步开关能量收集器（Synchronized Switch Harvester Based on Inductor， SSHI），电路中的电感元件可以在一定程度上增大压电片的电压幅值，从而提高系统的能量收集效果，整个能量收集系统通过集成电路的方式实现，实现起来也较为方便[5]。但SSHI电路中压电片电压幅值受限于电路的品质因子，而电路品质因子又是电路自身的固有特性，取值会受到限制，因此SSHI技术的能量收集效果也将受限于电路的品质因子[6]。Ji等[7]在研究中发现，利用负电容元件替换电路中的电感元件，形成的基于负电容的同步开关能量收集器（Synchronized Switch Harvester Based on Negative Capacitor， SSHNC），不仅能保证电压的“翻转”和放大，还能避免SSHI技术的能量收集效果受限于电路自身品质因子的缺点。在此基础上，研究人员又开发了自供能同步开关能量收集电路[8?9]，即利用收集到的电能给开关电路提供能量，实现了电路系统能量上的自给自足，扩大了同步开关能量收集技术的适用范围。

为了拓宽压电能量收集系统的工作频带，研究人员试图在能量收集系统中引入非线性因素，利用非线性系统动力学的特性，在更宽的频带内获得较好的能量收集效果。Liu等[10]和Zhao等[11]基于悬臂梁模型，在线性压电能量收集系统中引入冲击梁，使振动主梁与冲击梁构成一个双线性系统，拓宽了能量收集系统的工作带宽。Wu等[12]利用一个两自由度模型研究了三次非线性对线性压电能量收集电路的影响。文献[13?15]利用磁场作用在线性压电能量收集系统中引入双稳态非线性，采用时域分析方法对能量收集系统动力学特性进行了分析，并利用悬臂梁系统对分析结果进行了试验验证。Wang等[16]以悬臂梁为模型，在线性压电能量收集系统中同时引入双稳态和双线性因素，其研究表明双线性因素可以使双稳态压电能收集系统的能量收集效果进一步获得提升。

分析发现，现有文献中的研究大多是在线性压电能量收集电路中引入非线性因素，并利用时域分析方法或试验研究的方法对能量收集系统的动力学特性进行研究。而由于同步开关电路自身的非线性特点等因素，在效果更好的同步开关能量收集系统中引入非线性因素，进一步提升同步开关电路工作带宽和能量收集效果的相关研究鲜有报道。本文提出了一种基于同步开关电路的非线性宽频压电能量收集系统，在同步开关能量收集系统中引入具有冲击作用的副梁，探索在更宽的频带内获得较好的能量收集效果的方法，并从理论上对能量收集系统的动力学特性进行了研究。

1 能量收集系统动力学模型

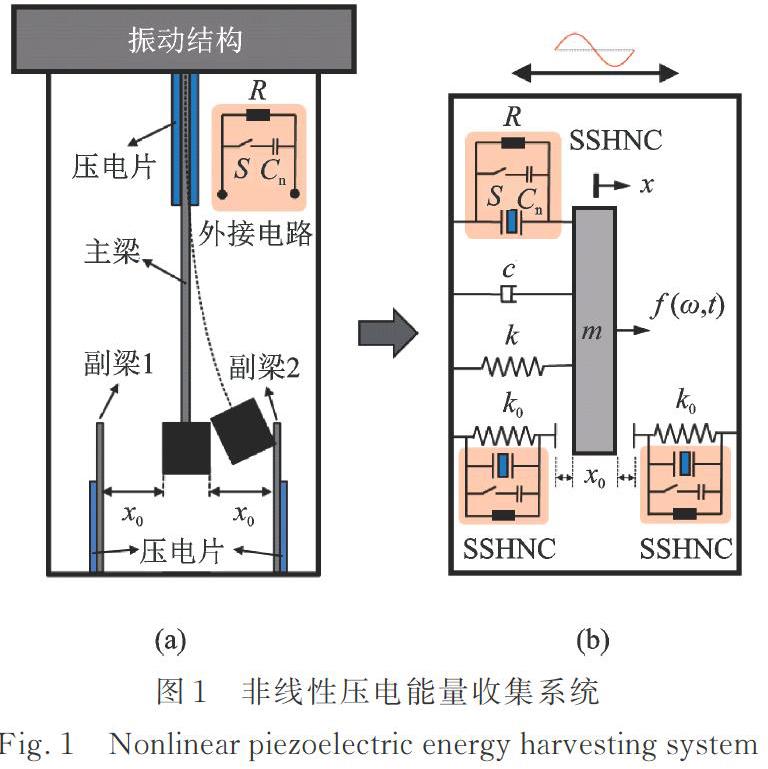
压电能量收集系统如图1（a）所示：在与振动结构相连的刚性框架内设置一个悬臂梁（后文称之为“主梁”），悬臂梁与其自由端的刚性质量块构成“弹簧?振子”系统。悬臂梁自身质量相对于质量块可以忽略，悬臂梁主要提供“弹簧?振子”系统的刚度。在刚性框架中与质量块两侧距离为的位置分别再设置一个悬臂梁（后文分别称之为“副梁1”和“副梁2”），当结构发生振动时，刚性框架随之运动，连接质量块的主梁也随之振动，当振动幅值足够大时，副梁与质量块发生接触并随之振动（忽略碰撞造成的能量损失）。副梁质量相对于质量块也可以忽略，其主要作用为在与质量块发生接触时改变“弹簧?振子”系统的刚度。在主梁及副梁根部位置分别粘贴有压电片，压电片的正压电效应可以将悬臂梁因振动产生的应变能转化为电能，进而通过压电片电极之间外接的同步开关电路收集起来，以实现对结构振动能量的收集。

由于三个悬臂梁的质量相对于质量块可以忽略，且压电片粘贴在梁根部，压电片主要感受悬臂梁一阶模态振型的应变，能量收集系统主要收集梁的一阶振动能量，这样，对图1（a）中的能量收集系统动力学特性的分析可以转化为对图1（b）所示系统的分析。图1（b）中为质量块质量，为主梁的刚度，为副梁的刚度，为机械阻尼系数，为副梁与质量块之间的初始间隙。在质量块振动的过程中，除了受到激振力的作用，还会受到压电片产生的机电耦合作用力，以及副梁产生的作用力，因此，整个能量收集系统的动力学方程可以表示为

如图1（b）所示，在压电片两电极之间连接一个同步开关（用表示，实际中利用电路实现），以及一个负电容元件（表示，实际中通过模拟电路实现）。同步开关电路在实现电压方向“翻转”同时，还能实现电压幅值的“放大”，进而提升了与开关元件并联支路的能量收集能力，这种同步开关电路被称为基于负电容的同步开关能量收集器（SSHNC）。

对于SSHNC系统，在一个振动周期中，压电片电极电压与振动位移之间的关系如图2所示。在实际中，同步开关的作动时间一般远小于结构振动周期，即在一个振动周期中，开关处于闭合状态的时间远小于开关处于断开状态的时间[5]。由压电传感方程可知[6]，同步开关闭合前后的电压幅值，以及结构振动幅值之间存在如下关系

式中  为压电片的内置电容，为压电片的力系数，实际中这两个参数均可通过试验测得[6]。为了方便，在进行理论分析时可以忽略开关闭合的瞬间[17?19]，结合式（2）及开关电路的工作原理可得SSHNC电极电压的表达式为

式中  表示符号函数，为SSHNC電路中负电容值的大小与压电片内置电容值之比，即

从表达式（2）可以看出，电压的幅值与成正比，且为结构振动位移及振动速度的非线性函数，因此具有SSHNC的机电耦合系统为典型的非线性系统，文献[6?7]的相关实验研究验证了式（3）的合理性。在式（3）中，由于，因此等号右边第一项的绝对值始终大于或等于第二项的绝对值，也就是说电压的方向始终与结构的振动速度的方向相反。由此可见，在收集量的同时，SSHNC还将产生一个阻碍“弹簧?振子”系统振动的机电耦合作用力，且力的大小与压电片电极电压成正比[7]，其数学表达式为

由同步开关电路的工作原理可以看出，同步开关电路不同于以往基于电路谐振的线性能量收集系统[2]，电路不需要与系统进行“调谐”，因此基于同步开关电路的能量收集系统具有更宽的工作频带。

当质量块与副梁接触时，副梁会对质量块产生反作用力。由于副梁根部粘贴有压电片并连接有能量收集电路，除了副梁自身刚度产生的反作用外，压电片也会对副梁产生机电耦合作用力，而该力最终也将通过副梁传递到质量块上。因此，共包含两部分，其表达式为

式中  为副梁自身刚度产生的作用力，该作用力具有“双线性”的特点（如图3所示），其数学表达式如下式所示

文献[11]的相关实验研究验证了式（7）的合理性。

为压电片通过副梁对质量块的非线性机电耦合作用力，其大小与副梁根部压电片电极电压成正比，数学表达式为：

为使研究具有更广泛的意义，对能量收集系统的非线性机电耦合动力学方程（1）进行无量纲化，无量纲原则为

将上述无量纲原则带入式（1）可得能量收集系统的无量纲非线性机电耦合动力学方程为

其中，无量纲非线性力数学表达式分别为：

2 频域分析方法

2.1 非线性系统频域响应计算方法

方程（10）含有多种非线性因素，其动力学特性的分析（特别是频域响应的求解）存在一定的难度。虽然直接积分法求解非线性动力学方程的计算精度很高，但计算效率较低，如果采用直接积分法获得系统的频响曲线，会耗费大量的计算时间。谐波平衡法作为一种经典的非线性系统求解方法具有很多优势，几乎能够处理包括几何非线性、接触非线性、材料非线性在内的各种强/弱非线性问题，是一种高效、可靠的计算方法[17?19]。但是，对于强非线性系统，只保留一阶谐波的谐波平衡法很难保证求解精度[20]，由此发展了保留更多谐波阶次的高阶谐波平衡法（Multi?Harmonic Balance Method， MHBM）。

任意离散非线性系统的自由振动方程可以表示为如下形式

式中  为系统所受的非线性力。首先将系统的周期解展开成傅里叶级数的形式

式中  为计算过程中保留的谐波阶次，保留的谐波阶次越多，计算结果越精确，计算量也会随之上升。

将非线性系统振动幅值的傅里叶系数写成向量的形式为

同理，将系统激振力及非线性力展开成傅里叶级数的形式：

激振力及非线性力的傅里叶系数的向量形式为：

将式（11）和（13）代入式（10）中，利用伽辽金过程将非线性系统的动力学微分方程组从时域转换到频域，得到非线性系统的频域代数方程组

式中  为动刚度矩阵，其表达式为：

其中矩阵子块表达式为

对于较为复杂的系统，利用高阶谐波平衡法（MHBM）求解时，当保留的谐波阶次大于3（即）时，方程组（21）的解析形式难以直接写出，此时可以采用Cameron等[20]提出的时频转换（Alternation Frequency/Time Domain Method， AFT）技术，利用快速傅里叶变换程序完成分析过程中的正逆傅里叶变换。

在使用牛顿迭代法对非线性代数方程组（21）进行求解时，为确保非线性求解过程的收敛性，可以引入弧长延拓技术。弧长延拓技术包括“预测步”和“校正步”两个基本步骤，其基本思路为：

对方程进行泰勒展开，并保留一阶精度可得

式中  为预测步的增量向量。为保证预测点与初始点之间的距离始终为，可以得到如下关系

根据式（24）和（25）可以求得预测步的增量向量。由增量向量可以获得预测点的位置为，然后对预测点进行校正：以为中心，为半径的圆与函数“曲线”的交点即为系统的解。因此，非线性方程组校正后的解可由以下方程确定

一般选择合适的，并经过数次校正之后就可以获得收敛的非线性系统的频域响应，非线性系统频域响应计算流程如图4所示。

2.2 非线性系统稳定性分析方法

与线性系统不同，非线性系统可能存在不稳定的周期解，本文采用Hill法[21]对周期解的稳定性进行分析。假设非线性系统周期解受到一个扰动，则时域响应可以写为

将代入方程（14）中，并利用谐波平衡法将时域中的非线性方程组转化为频域中的非线性代数方程组

对式（34）对应的特征方程进行求解，可以获得一系列的复特征值。当系统的全部复特征值的实部都小于0时，方程的解稳定，当存在实部大于0的特征值时，方程的解不稳定。

2.3 算例分析

利用MHBM法对经典的Duffing系统的频域响应进行求解（计算过程中保留5阶谐波），并利用Hill法对解的稳定性进行分析。Duffing系统的动力学方程为

不同激励频率下，特征值实部如图5所示，对应的频响曲线如图6所示。通过与文献[22]中典型的Duffing系统计算结果进行对比，表明当保留足够多的谐波阶次时（保留的谐波阶次数可根据非线性系统的具体性质来确定，一般谐波阶次大于5即可保证足够的求解精度），利用MHBM能够比较精确地求解非线性系统的频域响应，同时Hill法可以对频域响应的稳定性进行分析，后续将利用该方法对能够收集系统的频域特性进行分析。

3 能量收集系统动力学特性

3.1 能量收集系统频域响应

当副梁无量纲刚度，同步开关电路无量纲机电耦合系数（如无特殊说明，后文中取值均为0.1），电容比，无量纲激振力幅值为1，副梁与质量块初始间隙分别为，和时，系统频响曲线及其稳定性如图7所示。从图中结果可以看出，当初始间隙较大（）时，由于质量块无法与副梁发生接触作用，压电片的非线性力不能使能量收集系统频响曲线产生“歪头”现象。随着初始间隙的减小，质量块将与副梁发生接触，进而使系统频响曲线产生向右“歪头”的现象，且副梁与质量块之间的初始间隙越小，频响曲线向右“歪头”越明显。当初始间隙，副梁刚度分别为，和时，系统频响曲线及其稳定性如图8所示。可见，副梁与质量块之间的初始间隙一定时，副梁刚度越大，频响曲线向右“歪头”越明显。

初始间隙及副梁刚度一定时，当激励频率由小到大或由大到小变化时，系统频响曲线将会出现非线性系统典型的“跳跃”现象（如图9所示）。当频率由小到大变化时，能量收集系统产生较大振幅的频带更宽。由于压电片电极电压与悬臂梁根部应变水平成正比，而能量收集效果与压电片电极电压正相关，因此当振动频域由小到大逐渐变化时，副梁的存在可以拓宽能量收集系统的工作频带，获得更好的能量收集效果，接下来我们将针对这种情况进行分析。

3.2 能量收集系统频域输出功率

能量收集系统中主梁压电片电压以及两个副梁上压电片的电压分别用，和表示。当副梁刚度，同步开关电路电容比，副梁与质量块初始间隙，激振力幅值为1，激振频率为时，在两个完整振动周期内能量收集系统中压电片电压，及振动位移的时域曲线分别如图10和11所示。显然，在整个振动周期内主梁上的能量收集系统一直具有能量收集作用，而只有当质量块与副梁发生接触并使副梁发生变形时，副梁上的能量收集系统才具有能量收集作用。

为了对系统的能量收集效果进行评估，定义压电片在一个振动周期内向外电路输出的能量與振动周期之比为能量平均输出功率（后文简称“输出功率”），其物理意义为能量收集电路在单位时间内向外输出能量的平均值。对于压电片，输出功率可以表示为

式中  为压电片的输出功率，为压电片在一个振动周期内输出的电能，为主梁的振动周期，为压电片的无量纲内置电阻值，为外接电路中的无量纲电阻值。整个能量收集系统的总输出功率为

由式（37）可以看出，当外接电路中的电阻值与压电片内阻值相等时，压电片总输出功率最大，因此在后续分析中，均取。后续将利用输出功率作为评价指标，对不同参数下系统的能量收集效果进行评估，进而对系统设计参数进行优化。

当同步开关电路电容比为，无量纲激振力幅值为1，不同初始间隙及不同副梁刚度下，系统的总输出功率分别如图 12和 13所示。从图中的结果可以看出，虽然副梁会使同步开关能量收集系统在共振峰值附近的能量收集能力降低，但使得工作带宽大大拓宽，系统在整个工作频带上能够收集更多的能量。因此，在同步开关电路和副梁的共同作用下，使得该能量收集系统相比于以往的基于线性电路的双稳态能量收集系统更加适合于宽频域能量收集。

3.3 系统参数对能量收集效果的影响

3.3.1 同步开关电路参数对能量收集效果的影响

式（3）表明，压电片电极电压幅值主要取决于同步开关电路电容比，而电压幅值直接影响能量收集系统的输出功率，因此对输出功率具有决定性影响。当副梁系统参数（和）一定时，不同电容比下系统频响曲线及总能量输出功率曲线分别如图14和15所示。可以看出，当激振力幅值一定时，同步开关电路电容比越大，系统在共振峰附近的振动峰值越小，能量收集系统在共振峰值附近的能量收集能力越强。当电容比过大（如）时，系统振动幅值过小，质量块与副梁无法相互接触，副梁无法起到拓宽能量收集系统工作带宽的作用。因此，适当减小电路中的电容比，虽然会降低系统在共振峰附近的能量收集能力，但可以拓宽系统的工作频带。实际中可根据能量源的频率变化范围来选择同步开关电路的电容比，以兼顾能量收集系统的工作带宽和能量收集效率。

3.3.2 副梁參数对能量收集效果的影响

取同步开关电路电容比，当副梁刚度时，初始间隙对系统的输出功率及工作带宽的影响规律如图16所示。而当初始间隙时，副梁刚度对系统的输出功率及工作带宽的影响规律如图17所示。可见，副梁与质量块的初始间隙以及副梁刚度对能量收集系统工作带宽以及输出功率具有较大影响。副梁与质量块的初始间隙越小，副梁的刚度越大，能量收集带宽越宽，但最大输出功率也会有所下降。需要指出的是，由于同步开关能量收集电路自身的能量收集能力较强[4?5]，因此即使输出功率有所下降，同步开关电路相比于传统的被动能量收集系统依然具有很好的能量收集效果，应根据振动环境的频率变化范围以及激振力幅值水平，对能量收集器进行合理的设计，进而获得更好的能量收集效果。

副梁的无量纲刚度时，初始间隙对副梁输出功率占系统总输出功率的百分比的影响规律如图18所示。当初始间隙为时，副梁刚度对副梁输出功率占比的影响规律如图19所示。根据分析结果可知，当初始间隙较小，副梁刚度也较小时，副梁的能量收集效果较好（占总输出功率的10%左右）。可见，虽然主梁的输出功率仍在能量收集系统的总输出功率中占主导，但在特定频带内，副梁上布置的能量收集器也会为整个系统的能量收集带来比较可观的贡献。

4 结  论

在基于同步开关电路的压电悬臂梁能量收集系统中引入副梁，形成一种非线性宽频压电能量收集系统，并利用高阶谐波平衡法对系统频域响应及能量收集效果进行了理论研究，为该非线性宽频能量收集系统的应用提供依据。分析结果显示：①非线性同步开关电路的引入，拓宽了传统线性压电能量收集电路的工作频带，而副梁的引入可以进一步拓宽基于同步开关能量收集系统的工作带宽。在同步开关电路和副梁共同作用下，使得该能量收集系统相比于以往基于线性电路的双稳态能量收集系统更加适合于宽频域能量收集;②适当减小同步开关电路的电容比及副梁与质量块间的初始间隙、增大副梁刚度，虽然会降低系统在共振峰附近的能量收集能力，但可以拓宽系统的工作频带;③实际中振动能量源往往具有宽频特点，因此，除了保证共振峰附近的能量收集能力，还要关注一定频带宽度上的总能量收集效率。需结合振动能量源频率带宽及能量的频域分布规律，对系统关键参数进行匹配设计，以获得最佳能量收集效果。

参考文献：

[1] Mitcheson P D， Yeatman E M， Rao G K， et al. Energy harvesting from human and machine motion for wireless electronic devices[J]. Proceedings of the IEEE， 2008，96（9）：1457-1486.

[2] Leland E S， Wright P K. Resonance tuning of piezoelectric vibration energy scavenging generators using compressive axial preload[J]. Smart Material Structures， 2006， 15（5）：1413-1420.

[3] Hagood N W， von Flotow A. Damping of structural vibrations with piezoelectric materials and passive electrical networks[J]. Journal of Sound and Vibration， 1991， 146（2）： 243-268.

[4] Richard C， Guyomar D， Audigier D， et al. Semi-passive damping using continuous switching of a piezoelectric device[C]. Smart Structures and Materials 1999： Passive Damping and Isolation International Society for Optics and Photonics， Newport Beach， CA， USA，1999：104-111.

[5] Richard C， Guyomar D， Audigier D， et al. Enhanced semi-passive damping using continuous switching of a piezoelectric device on an inductor[C]. Smart Structures and Materials 2000： Damping and Isolation， Newport Beach， CA， USA， 2000： 288?299.

[6] 季宏丽. 飞行器结构压电半主动振动控制研究[D]. 南京： 南京航空航天大学， 2012.

Ji Hongli. Research on piezoelectric semi-active vibration control of aircraft structures[D]. Nanjing： Nanjing University of Aeronautics and Astronautics， 2012.

[7] Ji H， Qiu J， Cheng J， et al. Application of a negative capacitance circuit in synchronized switch damping techniques for vibration suppression[J]. Journal of Vibration & Acoustics， 2011， 133（4）：041015.

[8] Lallart M， Guyomar D， Jayet Y， et al. Synchronized switch harvesting applied to self-powered smart systems： Piezoactive microgenerators for autonomous wireless receivers[J]. Sensors and Actuators A： Physical， 2008， 147（1）： 263-272.

[9] Eltamaly A M， Addoweesh K E. A novel self-power SSHI circuit for piezoelectric energy harvester?[J]. IEEE Transactions on Power Electronics， 2017，32（10）：7663-7673.

[10] Liu S， Cheng Q， Zhao D， et al. Theoretical modeling and analysis of two-degree-of-freedom piezoelectric energy harvester with stopper[J]. Sensors and Actuators A： Physical， 2016， 245：97-105.

[11] Zhao D， Wang X， Cheng Y， et al. Analysis of single-degree-of-freedom piezoelectric energy harvester with stopper by incremental harmonic balance method[J]. Materials Research Express， 2018，5（5）：055502.

[12] Wu Yipeng， Ji Hongli， Qiu Jinhao， et al. A 2-degree-of-freedom cubic nonlinear piezoelectric harvester intended for practical low-frequency vibration[J]. Sensors and Actuators A： Physical， 2017， 264： 1?10.

[13] Gao Y J， Leng Y G， Fan S B， et al. Performance of bistable piezoelectric cantilever vibration energy harvesters with an elastic support external magnet[J]. Smart Materials and Structures， 2014，23（9）：1-14.

[14] Lan Chunbo， Qin Weiyang. Enhancing ability of harvesting energy from random vibration by decreasing the potential barrier of bistable harvester[J]. Mechanical Systems and Signal Processing， 2017，（85）：71-81.

[15] Fang Hongbin， Wang K W. Piezoelectric vibration-driven locomotion systems——Exploiting resonance and bistable dynamics[J]. Journal of Sound and Vibration， 2017，391： 153-169.

[16] Wang Chen， Zhang Qichang， Wang Wei. Low-frequency wideband vibration energy harvesting by using frequency up-conversion and quin-stable nonlinearity[J]. Journal of Sound and Vibration， 2017， 48（2）： 169-181.

[17] Liu Jiuzhou， Li L， Huang X， et al. Dynamic characteristics of the blisk with synchronized switch damping based on negative capacitor?[J]. Mechanical Systems and Signal Processing， 2017，95： 425-445.

[18] Liu J， Li L， Fan Y. A comparison between the friction and piezoelectric synchronized switch dampers for blisks?[J]. Journal of Intelligent Material Systems and Structures， 2018， 29（12）：2693-2705.

[19] Liu Jiuzhou， Li Lin， Fan Yu， et al. A modified nonlinear modal synthesis scheme for mistuned blisks with synchronized switch damping?[J]. International Journal of Aerospace Engineering， 2018， 2018： 8517890.

[20] Cameron T M， Griffin Jerry H. An alternation frequency/time domain method for calculation the steady-state response on nonlinear dynamic system?[J]. Journal of Applied Mechanics， 1989， 56（1）：149-154.

[21] Zhou B， Thouverez F， Lenoir D. Essentially nonlinear piezoelectric shunt circuits applied to mistuned bladed disks[J]. Journal of Sound and Vibration， 2014， 333（9）： 2520-2542.

[22] Laxalde D. Stability analysis of periodic orbits in the framework of Galerkin approximations?[J]. 2011：hal-00655521.

作者简介： 刘久周（1988?），男，工程师。电话：13401177057; E-mail： liujiuzhou123@126.com