黄土高原坡度因子的多重分形谱特征
2021-08-09夏积德丛佩娟李俊锋
夏积德, 丛佩娟, 李俊锋
(1.杨凌职业技术学院, 陕西 杨凌 712100; 2.水利部 水土保持监测中心, 北京 100053; 3.陕西测绘地理信息局, 陕西 西安 710054)
地形因子是水土流失、水文过程模拟的参数,科学量化地形因子对于水土流失这一地理界面过程的研究具有极为重要的意义。大量研究发现,自然界中大部分区域的地表形态复杂多变,呈现出明显的不均匀性和分形特征,即具有以非整数维形式充填空间的形态特征。若仅采用普通分形维数的方法并不能详细且全面地反映不同区域条件、不同尺度下的地形因子特征。在多重分形理论被提出后,由于其采用广义维数和多重分形谱来描述分形客体,考虑了对象属性在几何支集的空间奇异性分布这一特点[1],即能考虑到复杂分形体内部不同区域呈现出不同分形特征,因而逐渐被用于包括地形地貌学在内的各种地理学相关研究。沈中原等[2]借助多重分形理论构建了海拔信息空间分布概率计算模型;张建兴等[3]探讨了黄土高原若干流域的河网分形特征并基于此建立起产沙模数模型;王民等[4-5]运用多重分形理论及其实现方法分析了大理河流域地表形态的多重分形特征。这些研究多运用分形理论表征区域地貌形态的综合特征[6],但对于黄土高原地区地形因子(如坡度)的多重分形研究还很少涉及。因此,本文运用多重分形理论来研究黄土高原地区地形因子的特点,旨在为黄土高原地区开展地形因子方面的研究提供参考。本研究对区域水文过程、水土流失预报模型的建立具有积极意义。
1 研究区概况
黄土高原地处中国中北部地区,辖内蒙古、山西、陕西、宁夏、甘肃、青海、河南7个省区,东西跨越1 000 km多,南北跨越近750 km,总面积约为6.40×104km2,海拔高度介于1 000~3 000 m,是中国4大高原之一。黄土高原整体表现出西北高东南低的特点,宁夏西南方的六盘山和山西西部的吕梁山将整个黄土高原划分为3个部分,在此划分基础上进一步按照地形地貌特点将黄土高原划分为山地区、黄土丘陵区、黄土塬区以及河谷平原区4种类型。山地区主要包括马衔山地区、拉脊山地区、六盘山地区、子午岭地区、太行山地区和吕梁山地区,海拔跨度大、地形地貌差异较大,由于长期受重力、流水以及风力等侵蚀因素的影响,山地区的地貌侵蚀现象严重,沟壑明显,坡度较大;丘陵区作为黄土高原地区较为典型的地形地貌区域有着十分广阔的分布区域,其占据了超过黄土高原地区一半的面积。丘陵区在黄土高原分布范围辽阔,不同区域的丘陵区之间还存在不小的差异;黄土塬区中分布着大量塬面,塬面顶部十分平坦,地形复杂程度较低。与之形成强烈对比的是塬面周围陡峭的沟壑,这些沟壑分布在一个又一个塬面之间,使得黄土塬区内部的地形地貌形成了十分大的反差,地形复杂度对比强烈;河谷平原区以关中平原最具代表性,关中平原位于陕西省中部,呈东西带状分布,地形较为单一,多为平原,在长期的冲击下形成了平坦开阔的地貌景观。
2 研究方法
在黄土高原不同地貌类型区内选择合适的研究区,获取各子研究区的DEM(来源于地理空间数据云(http:∥www.gscloud.cn/,空间分辨率为30 m×30 m,并在GIS中提取得到坡度因子的栅格数据;随后,采用盒维数的计算方法,计算得到坡度因子的多重分形谱并对其主要参数及图像特征进行对比分析。
2.1 多重分形谱的计算
盒维数方法是一种基于统计学原理的计算多重分形的方法,具有简便且易于理解的特点,经常被用于地形地貌多重分形的计算[7]。盒维数是用一系列紧密相连的正方形盒子去覆盖分形体,即将研究对象分为很多个(假设有i行j列总计N个)尺度大小为r的正方形网格单元[8],然后计算每个网格单元内的概率测度。对于坡度因子来说,概率测度的大小可以用坡度概率函数表示,每个小网格单元的坡度概率函数的计算公式为:
(1)
式中:Pij(r) 表示位于第i行第j列的网格的坡度概率函数;Air(r)表示位于第i行第j列的网格内的坡度统计值;N表示网格单元的总个数,其在数值上满足:N=i×j。
根据公式(1)并结合多重分形理论[9-10]可知,坡度概率函数可以粗略衡量一个网格单元区域的地形特点,数值越小表示该网格区域内坡度越小,具有越平坦的地形特点,如塬面、平原等;反之,坡度概率函数的数值越大表示网格区域内的坡度越大,地形起伏程度越大,如峁、坡面等。
在盒维数方法中,检验一个研究对象是否具有多重分形特征,有一个配分函数的概念[11],配分函数的计算公式如下:
(2)
式中:Xq(r)表示分形体的配分函数;Pij(r)表示位于第i行第j列的网格的坡度概率函数;q表示阶矩,可以取任意实数,配分函数中q的取值直接影响着不同的概率测度在整个配分函数上所占比重的大小。
对于给定的一对r和q,都可以通过公式(1)和公式(2)计算得到一个配分函数。在盒维数方法中,如果研究对象具有多重分形特征,那么配分函数Xq(r)和r之间应该满足以下的关系[12]:
Xq(r)∝rτ(q)
(3)
式中:τ(q)是关于q的一个表达式,在探讨研究对象是否具有多重分形特征的过程中无关紧要。
根据上述关系可知,对两边同时取对数,lnXq(r)和lnr满足线性关系。因此绘制以lnr为横轴,lnXq(r)为纵轴的散点分布图,对其拟合,如果lnXq(r)—lnr图像为一系列斜率不等的直线,则表明研究对象具有多重分形特征[13],可以进一步计算其多重分形谱及其特征参数。
本研究利用Chhabra等[14]提出的一种建立在盒维数方法基础上的通过拟合参数计算多重分形谱的方法来计算多重分形谱。这种方法需要设立一个经过归一化处理的测度集μij(q,r),其计算公式如下:
(4)
在这个测度集的基础上结合多重分形的概念,可以通过下面的公式来计算多重分形中的奇异指数α和分形维数f(α):
(5)
(6)
奇异指数α是一个标度指数,它是反映分形体内各个小区间的奇异程度的一个量,α的数值与其所在的位置有关。将分形上具有相同α值的小区间数记为f(α),基于此可以得到α—f(α)的函数图像,称为奇异谱。横坐标的范围是多重分形谱奇异指数α的分布范围,α的大小反映该部分的奇异程度。
在计算时,常常按照公式(5)和公式(6)的数学几何意义借助拟合的方法来得到α和f(α)的值。将公式(5)处理可得:
(7)
公式(7)根据一次函数相关概念及其图像性质可知α为∑μij(q,r)·lnPij(r)—lnr图像的斜率,类似地,f(α)为∑〔μij(q,r)·lnμij(q,r)〕—lnr图像的斜率。
首先确定一个q值,保持阶矩q不变而改变尺度r,每选取一个r进行计算,按照公式(1),(2),(4)就可以得到一个对应的∑μij(q,r)·lnPij(r)—lnr和∑〔μij(q,r)·lnμij(q,r)〕,通过在二维坐标系中进行拟合便可得到每个q对应的奇异指数α和分形维数f(α)。改变阶矩q的值,便能得到一系列的α和f(α),而多重分形谱就是以α为横坐标,f(α)为纵坐标的图像。
2.2 特征参数的取值
(1) 格网大小(尺度)r的选取。根据多重分形理论,格网的大小直接影响到格网的总数量和每个格网的概率测度,这两个因素决定着多重分形计算过程中的效率和准确性,因此从简便、可实施的角度出发,需选取大小为30 m整数倍的格网来覆盖研究区。结合所选4个研究区坡度数据的实际情况,规定一个栅格大小即30 m为一个单位,通过反复试验最终选取格网尺度大小为20,30, 40,…,190,200个单位,亦即600,900,1 200,…,5 700,6 000 m,共19种。
(2) 阶距q取值范围的确定。公式(3)配分函数中q的取值直接影响着不同的概率测度在整个配分函数上所占比重的大小[15],当q取正值且取值越大,配分函数越能反映具有较大坡度概率函数的那些网格单元的特征和性质;当q取负值且取值越小,则配分函数越能反映具有较小坡度概率函数的那些网格单元的特征和性质。因而q的取值对配分函数的计算结果影响很大,不同区域坡度的位置分布和大小范围不同,各研究区q的取值范围也不同,研究表明,在地形地貌多重分形的计算中,q值分布在0左右且通常介于±30之间[4]。
本研究对每一个子研究区在-50~50之间等间距选取不同的q值,通过盒维数计算多重分形谱的方法验证q是否在合适的区间。在初步确定q的合适区间后继续加密q的取值,最终得到每个研究区阶矩q的最佳取值范围见表1。

表1 研究区q最佳取值范围
3 结果与分析
3.1 坡度概率分布特点
为更详细、系统地了解各研究区坡度大小的分布情况,对4个研究区的坡度进行统计(图1)。可以看出,山地区、黄土丘陵区、黄土塬区、河谷平原区的坡度介于0°~10°之间的栅格占比分别为35.80%,35.50%,60.75%,>99.99%;介于10°~20°之间的栅格占比分别为24.23%,40.59%,16.94%,<0.01%;介于20°~30°之间的栅格占比分别为20.48%,20.92%,13.74%,0%;介于30°~40°之间的栅格占比分别为15.76%,2.89%,7.54%,0%;介于40°~50°之间的栅格占比分别为3.63%,0.10%,1.02%,0%;介于50°~60°之间的栅格占比分别为0.1%,0%,0.01%,0%。
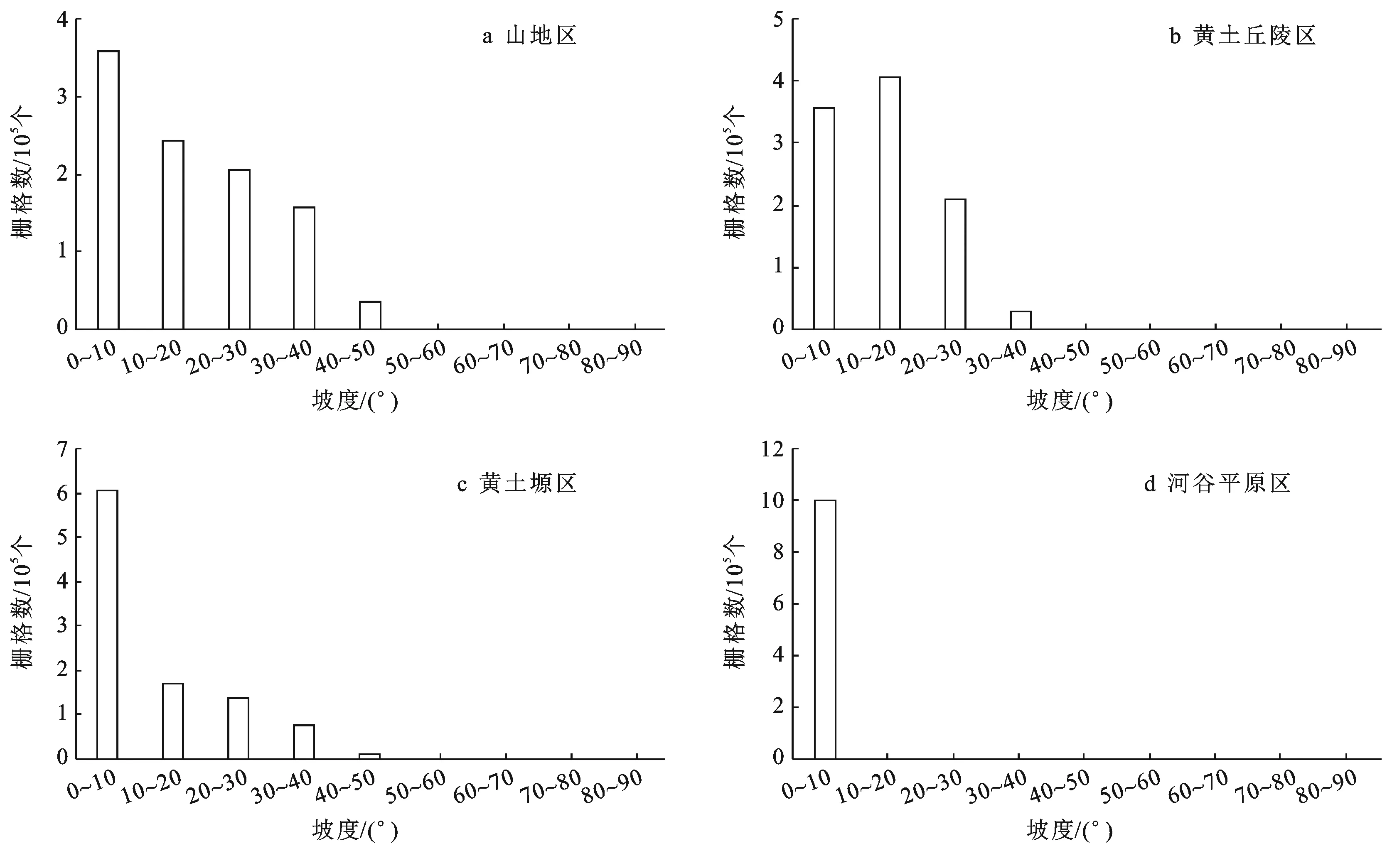
图1 研究区不同地形坡度统计
由统计结果得知:①山地区的坡度分布区间最大,大部分栅格处于0°~20°这一中小坡度区间,坡度大于40°的区间在4个研究区中占比最高;②黄土丘陵区坡度介于0°~10°区间内的占比最少,坡度大部分位于10°~20°这一坡度范围内。同时,大于30°的坡度占比较小,因此在黄土丘陵研究区内大坡度的地形较少,地形特点较为均一;③黄土塬区有大面积的平坦塬面,坡度大部分介于0°~10°之间,因此坡度值往往很小,由于所选研究区面积固定为30 km×30 km,在这样一个较大的范围内不可避免地包括了塬面周围的切沟、坡面等非塬面地形,因此也存在少量坡度大于20°的非塬面特征栅格;④河谷平原区的坡度统计图特征十分明显,几乎所有栅格的坡度均介于0°~10°之间,在4个研究区中地形最为平坦。
3.2 多重分形特征检验结果
在计算坡度信息多重分形谱前需要先验证研究对象是否具有多重分形特征。为此,在平面坐标系中,以lnr为横坐标,lnXq(r)为纵坐标,绘制出每个研究区的lnXq(r)曲线,4个研究区坡度地形因子绘制的lnXq(r)—lnr曲线见图2。
从图2中可以看出,每个研究区在各自合适的q范围内,当尺度对数满足3.0≤lnr≤5.3时,配分函数对数与尺度对数之间存在很好的线性关系,表明黄土高原区域上述4个研究区的坡度信息具有明显的多重分形特征,可以进行多重分形谱的计算。

图2 研究区不同地形lnXq(r)-lnr特征
3.3 坡度信息多重分形谱及其参数
以坡度数据为基础,利用多重分形理论原理和计算方法得到研究区坡度信息多重分形谱散点分布图(图3)及其参数结果(表2)。由图3的多重分形谱可以看出,不同研究区的多重分形谱均为凸函数。在一个研究区内,多重分形谱函数值随着坡度奇异指数的增加均呈现出先递增后递减的变化特征。而在各研究区之间,坡度多重分形谱的对称性、图像分布范围均有不同,这是由于各研究区多重分形谱参数的差异导致的。通过对多重分形谱图的二维坐标系进行拟合,得到各研究区详细的多重分形谱参数信息见表2。
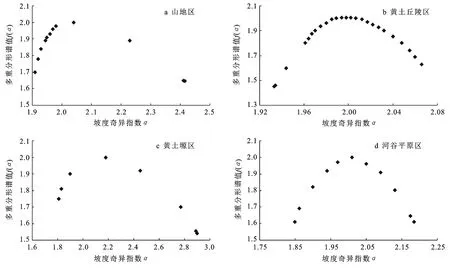
图3 研究区不同地形多重分形谱特征

表2 研究区多重分形特征参数
从多重分形谱参数统计表中可以看出,最小坡度奇异指数的最大值为1.94,出现在黄土丘陵区,最小值为1.82,出现在黄土塬区,说明在4个研究区中,坡度最大的地貌单元出现在黄土塬区(奇异指数最小值对应的是坡度最大地貌单元的性质);最小坡度奇异指数相应的多重分形谱值的最大值为1.78,出现在黄土塬区,最小值为1.45,出现在黄土丘陵区,这说明最小坡度奇异指数对应的地貌类型单元在黄土塬区所占比例最大,这与鲁克新等[16]的研究结果相一致,在黄土丘陵区所占比例最小,即坡度最大的子区域在黄土塬区占比最高,而在黄土丘陵区占比最低;最大坡度奇异指数的最大值为2.90,出现在黄土塬区,最小值为2.07,出现在黄土丘陵区,说明地形特征最简单的地貌单元出现在黄土塬区;最大坡度奇异指数所对应的多重分形谱值最大值为1.63,出现在河谷平原区,最小值为1.56,出现在黄土塬区,说明最大坡度奇异指数对应的地貌类型单元在河谷平原区所占比例最大,在黄土塬区所占比例最小。黄土塬区对应的坡度奇异指数的极值最大,为1.08,山地区次之,为0.50,然后是河谷平原区的0.35,而黄土丘陵区为0.13。
在多重分形谱左端点值与右端点值之差这个参数上,从绝对值的大小来看,黄土塬区最大,数值为0.22,说明该研究区最小坡度奇异指数对应的地貌单元所占比例与最大坡度奇异指数对应的地貌单元所占比例的差异性最大,黄土丘陵区次之,差异性最小的是河谷平原区。从正负的角度来看,黄土丘陵区和河谷平原区为负值,山地区、黄土塬区为正值,说明前两个研究区的大坡度地貌单元所占比重较后两个研究区要小。
4 讨论与结论
目前,已有大量研究者采用简单分形维数、多重分形谱和联合多重分形等方法来表征复杂地貌的形态及其特征[17],但对于坡度因子的多重分形研究还很少涉及。本研究在DEM数据的基础上,将黄土高原按照不同地形地貌划分为山地区、黄土丘陵区、黄土塬区、河谷平原区,并对坡度因子的多重分形谱图像和多重分形特征参数进行了对比分析,总结出各自区域的多重分形谱特点,为后续开展黄土高原地形因子方面的研究打下了基础,对区域水文过程、水土流失预报模型的建立具有积极意义。
像元尺度的选取是地形因子分形维数计算的关键,像元尺度在范围之外时,地形因子的分形计算没有意义。本研究对研究区的多重分形特征进行验证,结果表明尺度对数满足3.0≤lnr≤5.3时,黄土高原地区坡度地形因子的配分函数对数与尺度对数之间的线性关系良好,表明黄土高原区域上述4个研究区的坡度信息具有明显的多重分形特征,可以进行多重分形谱的计算。
不同地形的多重分形谱图以及特征参数都有着明显的差异,其横坐标奇异指数α的大小反映该区域的奇异程度,这一参数的数值越大,表明分形体坡度特征的分异现象越大,其内部越不均匀、越复杂,两极化趋势越明显,α最小值、最大值所对应的多重分形谱值记为f(αmin),f(αmax),描述了小坡度单元区域和大坡度单元区域在整个研究区域内所占的比例高低。通过多重分形谱的研究可以发现,最小坡度奇异指数的最小值为1.82,相应的多重分形谱值的最大值为1.78,最大坡度奇异指数在4个研究区内最大,所对应的多重分形谱在4个研究区最小为1.57,说明坡度最小地貌单元在黄土塬区所占比例最小,坡度最大的地貌单元出现在黄土塬区且占比最高。黄土丘陵区、河谷平原区则表现出较小的奇异指数变化范围,黄土丘陵区最小坡度奇异指数的最小值为1.94,最大值为2.07,河谷平原区最小坡度奇异指数的最小值为1.85,最大值为2.19,相比之下地形较为均一。
通过多重分形谱与统计直方图对照研究可以发现,在4个研究区中,黄土塬区有不少坡度达到了40°,且坡度最大的地貌单元出现在黄土塬区且占比最高,在地势平坦的塬面出现这种情况是由于所选研究区面积固定为30 km×30 km,而单个塬面通常面积有限,在这样一个较大且规则的范围内不可避免地包括了塬面周围的切沟、坡面等非塬面地形,因此其坡度统计中也存在少量坡度大于20°的非塬面特征栅格,这也是黄土塬区的多重分形谱中奇异指数最小、对应的多重分形谱值在4个研究区中最大的原因,同时也反映了研究区地形复杂的特点。结合多重分形理论的相关知识发现,本研究结果与实际情况有着较好的对应,表明基于多重分形理论与方法对黄土高原地区的地形因子进行量化研究是可行的,为黄土高原地区开展地形因子方面的研究提供了参考,对区域水文过程模拟、水土流失预报模型的建立具有积极意义。可为黄土高原的地貌学研究、土壤侵蚀研究和水土保持规划工作的开展提供技术支持和帮助。
