四种元件的分数阶电路无源综合方法研究

梁贵书，张 静

(华北电力大学 电气与电子工程学院，河北 保定 071003)

0 引 言

传统电路综合理论已趋于完善，但分数阶元件的引入又给电路综合带来了新的挑战。由于分数阶导抗函数的复杂性，现阶段还无法提出通用的分数阶电路无源综合方法，只能对不同形式的分数阶导抗函数表达式采取不同的电路综合方法。

在多分数阶电路综合的研究中学者们进行了大量探索。文献[1]和[2]讨论了由单一分数阶电容与传统RLC元件组成的单口网络驱动点函数的实现问题。文献[3]和[4]研究了由两个分数阶元件(分数阶电容器或分数阶电感器)和一些电阻器组成的无源电网实现一类阻抗函数可实现性的充分必要条件。文献[5]从拓扑结构入手讨论了分数阶双二次阻抗函数最多可用4个元件以及5个元件实现的问题,然后拓展至六元件。文献[6]将分数阶函数进行变量代换，通过多变量谱分解[7]的方法给出了三变量导抗函数的达林顿无源综合方法。文献[8]通过阻抗换标和变量代换对两种元件电路和三种元件电路进行了综合，给出了综合方法。文献[10]讨论了分数阶网络的W域无源综合方法。

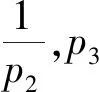
本文的其余部分组织如下：第1节将介绍一些预备知识。第2节给出了分数阶4种元件电路导抗函数的判别方法。第3节阐述了分数阶四种元件组成的分数阶电路的综合方法和具体的综合步骤，并给出了几个实例。第4节给出了综合方法的实例。第5节是文章的结论。

1 预备知识

1.1 分数阶元件

分数阶电感的伏安关系为

(1)

式中：α表示分数阶电感元件的阶次，本文简称(元件的)元次；Lα表示分数阶电感值，称为伪电感，其单位为H/s1-α。当0≤α≤1时，分数阶电感是无源的[28]。分数阶电感的符号如图1所示。

图1 分数阶电感的符号Fig.1 Circuit notations for fractional capaciton

零状态下分数阶电感的复频域伏安关系可写为

U(s)=LαsαI(s)

(2)

分数阶电容的伏安关系为

(3)

式中：α表示分数阶电容的元次；Cα表示分数阶电容值。当0≤α≤1时，分数阶电容是无源的[28]。分数阶电容的符号如图2所示。

图2 分数阶电感的符号Fig.2 Circuit notations for fractional inductor

1.2 分数阶无源四种元件电路

分数阶电路元件比整数阶电路更丰富，在此给出分数阶四种元件电路的定义。分数阶无源四种元件电路，本文简称分数阶四种元件电路，是指包含四种分数阶无源元件(包含传统的电容和电感)，或包含电阻与三种分数阶电抗元件的无源电路。

所含种类共包括CαCβCγCδ、LαCβCγCδ、LαLβCγCδ、LαLβLγCδ、LαLβLγLδ、RLαCβCγ、RLαLβCγ、RLαLβLγ、RCαCβCγ、LαCαCβCγ、LαLβCαCγ、LαLβLγCα、RLαCαCβ、RLαLβCα、LαLβCαCβ十五种情况。

分数阶四种元件电路的阻抗函数中最多包含四种元次。四元次阻抗函数的一般表达式为

(4)

式中：α、β、γ、δ分别表示阻抗函数对应电路中的四个元次。

1.3 阻抗换标与变量代换

对于一个单口无源网络，若对电路中所有阻抗进行换标因子为sγ的阻抗换标，那么驱动点阻抗也将变为原来阻抗的sγ倍，即Z′in=sγZin。在阻抗换标后，电路元件的种类会发生改变。

1.4 多变量正实矩阵与电抗矩阵的定义

定义1[6]一个多变量n×n矩阵Z(p1,p2,…,pk)是正实的，当且仅当

(1)对于实数pi(i=1,….k)，Z(p1,p2,…,pk)是实矩阵；

(3)当pi(i=1,….k)位于各自的扇形域内时，Z(p1,p2,…,pk)+ZH(p1,p2,…,pk)是半正定埃尔米特矩阵。

定义2[6]一个k变量n×n矩阵X(p1,p2,…,

pk)称为k变量电抗矩阵，是指

(1)X(p1,p2,…,pk)是正实矩阵；

(2)[X(p)+X(-p)]+[X(p)+X(-p)]T≡0n。其中，p=[p1,p2,…,pk]。

2分数阶四种元件电路导抗函数的判定方法

通过确定每个元次所含元件的种类数，可求得所有元次所含的元件的种类数。如果满足电抗函数中所有元次的元件种类和为4，或阻抗函数中所有元次的元件种类和为3，则可以确定此函数是分数阶四种元件导抗函数。通过1.2节分数阶四种元件电路的电路类型可知，分数阶4种元件电路导抗函数的元次个数应该是2或3或4。为了更好的表述，定义以下符号：k表示元次个数，且k∈{2,3,4}；(c+l)i表示电路中所含阶次为τi的电容电感的种类数，(c+l)i∈{1,2}；r表示电路中电阻的存在情况，且r∈{0,1}。在电路中，若只含有sτi的电容或电感则(c+l)i=1，若两者都有则(c+l)i=2；若Z(s)是电抗函数，则r=0，若Z(s)是阻抗函数则r=1。

分数阶4种元件阻抗函数判据：

下面给出一种判断电路中含有阶次为τi的分数阶元件种类数的方法。令阻抗函数Z(s)中sτi=s，sτj=cj(cj为任意正常数，j=1,2,…,k且j≠i)。即将电路中阶次为τi的分数阶电容、分数阶电感分别置换为整数阶电容、电感，将其余阶次分数阶电容和电感置换为电阻。通过改变cj的值，判断电路是否振荡，如果函数极点存在共轭复根，则(c+l)i=2，否则(c+l)i=1。

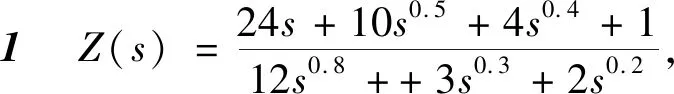
(5)

3四种元件电路导抗函数的无源综合

3.1 阻抗换标与变量代换

同样，为了方便理解，定义以下符号：τi(i=1,2,…,k),τi∈(0,1]是导抗函数中所含的元次；γa(a=1,2,3,4)是阻抗换标时用到的中间量，γa=-τi或τi或0；sγ是换标因子。

阻抗换标中间量γa的取值：根据元次τi所含元件种类依次确定γa的值。首先，根据元次τ1确定γa，若元次τ1仅含电容元件时，取γ1=-τ1；若元次τi仅含电感元件时，取γi=τi；若元次τ1含电容和电感元件时，取γ1=τ1,γ2=-τ1。其次，按照相同方法，根据τ2,…,τk确定γa(a的值在上一步的基础上顺延)。最后，若函数是阻抗函数，取γ4=0。

所以需要判断仅含一种元件的元次τi是含有电容元件还是电感元件。判断方法：令阻抗函数Z(s)中sτi=s，sτj=1(j=1,2,3,4且j≠i)，得Z″(s)。若Z″(s)极点的留数是正实数，则元次τi仅含电容元件，若Z″(s)极点的留数是负实数，则元次τi仅含电感元件。

分数阶四种元件电路导抗函数的无源综合步骤：

(1)确定四个中间量γa的值。

(3)进行变量代换

(a4=1,2,3,4;a4≠a1,a2,a3)，得函数Z(p1,p2,p3)。当且仅当2γa3-γa1-γa2≠0，2γa4-γa1-γa2≠0，γa2-γa1≠0，同时成立时，Z(p1,p2,p3)是三变量电抗函数。

通过三变量电抗函数综合方法对三变量电抗函数进行综合，无源实现为一个三变量电抗网络。

将所得无源网络进行逆变换，得到对应的分数阶四种元件电路。

3.2 三变量电抗函数综合方法

引理1[14]如果一个k变量正实矩阵X0(p1,p2,…,pk)在任意pi(1≤i≤k)的复平面无穷处有极点，那么X0(p1,p2,…,pk)可分解为

引理2[6]三变量电抗函数X(p1,p2,p3)最终可以实现为一个由p1类型的电抗、p2和p3类型的电感、理想变压器、回转器组成的单端口网络。

综合X0(p1,p2,p3)步骤如下：

(1)根据独立极点，分解函数X0(p1,p2,p3)，利用利用经典综合法实现单变量电抗函数X1，X2和X3。

(2)综合X(p1,p2,p3)，先提取p3型单位电感。

对X(p1,p2,p3)进行洛朗级数展开，得到

(6)

用g(p1,p2,p3)表示X(p1,p2,p3)最小公分母

(7)

令r×r的矩阵Nr-1(p1,p2)为

Nr-1(p1,p2)=

(8)

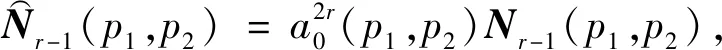
当r是奇数，且a0(p1,p2)=-a0(-p1,-p2)时，

(9)

其他情况下，

(10)

之后将M(p1,p2)分为Mi(p1,p2)，Mi(p1,p2)是k×1的矩阵，即

(11)

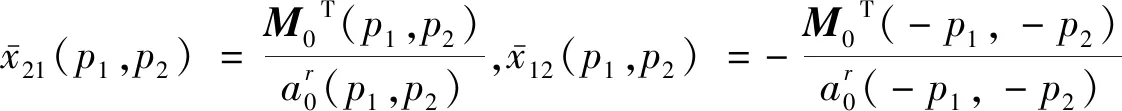
(12)

Ω(-p1,-p2)MT(-p1,-p2)

(13)

(3)将X0(p1,p2,p3)，X1，X2和X3网络串联。

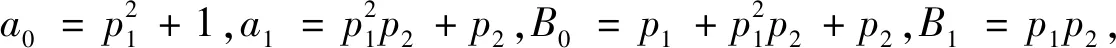
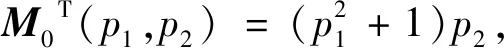
提取极点后，正好可分为两个单变量矩阵，实现的最终网络为

图3 导抗函数的网络Fig.3 Network of reactance function

对于一些满足如下定理的导抗函可以用以下综合方法。

引理3[20]一个正实有理函数Z(p1,p2,p3)=

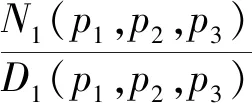
(1)degpiZ(p1,p2,p3)=1(i=2,3)

上面两个方程中的正号对应于负载等于pi(i=2,3)，负号对应于负载等于1/pi(i=2,3)。如果满足以上三个条件，那么综合过程是可以实现的，并且分为如图4四种情况。

图4 四种情况Fig.4 Four situations

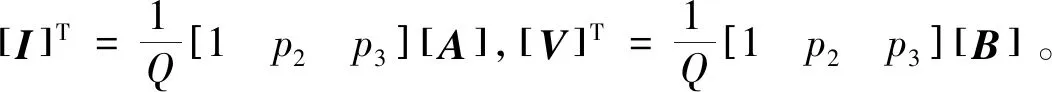
定理 当分数阶四种元件电路的两个阶次μ，δ分别只含有一个元件，其他阶次元件个数任意时，一定可以实现成驱动阻抗在端口1，且端口2和端口3分别接负载sμ，sδ的三端口网络。

证明 设电路中所含阶次为α，β，μ，δ，且其中阶次为μ，δ只含有一个元件，为了方便表述，设每种阶次所含的元件都是分数阶电感元件，所以换标中间量分别是γ1=α,γ2=β,γ3=μ,γ4=δ。

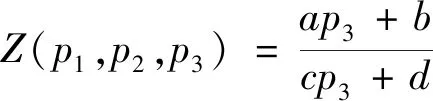
abcd是关于变量p1,p2的多项式，a′b′c′d′是关于变量p1,p3的多项式。

可知Z一定可以实现为如图5所示的网络[29]，因为原网络除p3元件外都是互易元件，所以N(p1,p2)一定是一个互易的二端口网络。

图5 二端口网络Fig.5 Two-port network

假设如图所示的二端口的开路阻抗矩阵为

表明上述综合过程是可行的，端口2和端口3分别为p2和p3，由端口电压电流性质可知

可知矩阵B是可逆的，得

最终网络实现如图6所示。

图6 最终实现的网络Fig.6 Finally realized network

对于另一类特殊的满足引理4的导抗函数可实现成一个单变量网络串联双变量网络。

引理4[29]多变量正实函数：Z(p1,p2,p3)，可以被分解为

Z(p1,p2,p3)=Z1(p1,p2)+Z2(p3)

(14)

的充分必要条件为

(15)

通过这个引理可以将三变量函数分解成一个单变量电抗函数和双变量电抗函数，再利用双变量电抗函数综合方法将其实现。

4 应用实例

分数阶电路模型在生物医学和生物学有广泛应用。在生物阻抗测量领域，由于Cole阻抗模型[30]结构简单且能与测量数据良好匹配，常用其表征生物组织和生化材料。Cole阻抗模型并不是唯一的。其中，由三个电阻和三个分数阶元件组成的电路，可以用于拟合从柳树根、茎、电极界面采集的阻抗数据，通过阻抗参数监测根系生长。下面通过一个例子来进行这种Cole模型的实现。

例4 根据参考文献[30]可知一个Cole模型阻抗表达式如式

所含的阶次分别α=0.5,β=0.7,μ=0.9。

根据分数阶四种元件判据可知此导抗函数是分数阶四种元件电路。然后确定阻抗换标中间量的值，经计算得元次α,β,μ都只含分数阶电容元件，所以取阻抗换标中间量为γ1=-0.5,γ2=-0.7,γ3=-0.9，此导抗函数是阻抗函数，所以γ4=0。

ZB(s)=s0.25·

=(s-0.25×4-0.45-0.65+s-0.25×2-0.45-0.65+

s-0.25×3-0.65+3s-0.25×3-0.45+

s-0.25-0.65+2s-0.24-0.45+2s-0.25-0.25+1)÷

(s-0.25×4-0.45+s-0.25×3+s-0.25×2-0.45+s-0.25)

根据引理4，可以将Z1(p1,p2)分解为Z1(p1,p2)和Z2(p3)

Z(p1,p2,p3)=Z1(p1,p2)+Z2(p3)=

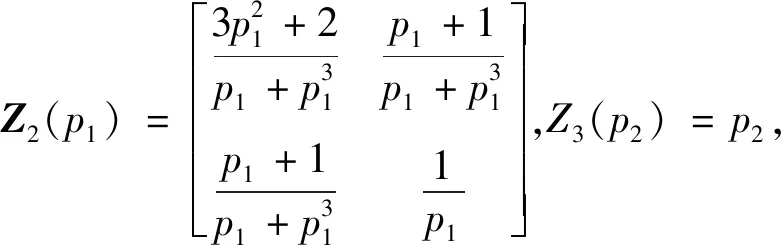
图7 在P域内实现的网络Fig.7 Network implemented in P domain

将电路中的变量反代换，且每个电路元件除阻抗换标因子sγ，得到电路图8。对所得电路进行仿真验证，“数学计算”是指基U(s)=I(s)Z(s)的分数阶阻抗函数Z(s)的数学计算；“电路仿真”是指通过改进节点法得到的分数阶网络端口电压。在图9中“数学计算”与“电路仿真”是一致的，所以综合网络的结果是正确的。

图8 导抗函数在s域内实现的网络Fig.8 Network realized by immittance function in s domain

图9 端口正弦稳态电压响应Fig.9 Network realized by immittance function in s domain

5 结 论

研究分数阶电路综合问题，能够推动电气工程领域器件设备的分数阶建模应用和精细仿真研究。本文提出了分数阶四种电路的判据和无源综合方法，通过示例，验证了方法的有效性。证明了当分数阶四种元件电路的两个阶次μ，σ分别只含有一个元件，其他阶次元件个数任意时，一定可以实现成驱动阻抗在端口1，且端口2和端口3分别接负载μ，σ的三端口网络。文中方法适用于任意的分数阶四种元件电路。本文的工作为后续分数阶多种元件电路综合研究奠定了基础。