基于独立分量分析的地震信号盲源分离及应用
2021-08-08孟会杰曾华会徐兴荣张小美
孟会杰,苏 勤,曾华会,徐兴荣,刘 桓,张小美
(中国石油勘探开发研究院西北分院,兰州 730020)
0 引言
实际采集的地震资料受野外采集条件的影响,通常包含严重的噪声干扰,资料信噪比较低,成像精度差。因此,地震资料的去噪优化处理对油气勘探至关重要[1]。提高地震资料信噪比是整个资料处理流程的关键,尤其是针对目前的复杂油气藏勘探,必须保证一定的信噪比。然而,由于实际采集的地震资料包含的噪声类型复杂多样,因此,在地震资料处理过程中寻找有效的去噪方法至关重要。
许多专家学者根据噪声和有效信号的特点,提出了不同的噪声去除方法来对地震资料进行处理。例如,基于域变换和滤波理论的噪声压制方法,包括t-x域、f-x滤波、f-k滤波、K-L变换等,这类方法主要是通过将待处理信号转换到某种域空间来消除噪声[2-5]。还有基于稀疏变换的去噪方法,如小波变换、Randon 变换、Curvelet 变换等[6-8],这些方法主要是通过将地震数据转换为稀疏域,然后对稀疏系数作阈值处理,再将处理后的稀疏系数转换到时空域达到去噪的目的[8-13]。通常这种变换为了达到所需要的去噪效果,在采用阈值函数对稀疏系数进行处理时,一般都是滤除小系数,保留少数较大的稀疏系数,即可反映原始数据的主要特征,这类方法也经常被用于实际资料处理中。然而,利用此类算法进行处理时,确定合适的阈值或者滤波器算子对去噪效果具有较大的影响,如果阈值较小或者滤波器算子较短,信噪分离程度低,处理后的资料中仍会存在较多噪声;反之,如果完全将噪声从资料中去除,难免也会伤及有效信号。
Herault 等[14]在一次计算机神经网络大会上首次提出盲源分离方法。独立分量分析(ICA)算法是随盲源信号分析理论发展而来的一种独立源信号提取算法,该概念最早是由Comon[15]提出。ICA 算法的基本思想是假设源信号相互独立,根据混合信号的高阶统计量信息,可以提取混合信号的各独立分量,并最终得到相互独立的源信号的最佳近似值。后经不断改进,该算法在各领域得到广泛应用。实际采集的野外地震资料,其有效信号和随机噪声是由不同信号源产生的,满足相互独立的特点。因此,可以利用ICA 算法对地震资料随机噪声进行压制。国内许多专家学者对ICA 算法进行了改进,并应用于地震资料噪声压制中,取得了不错的效果。刘喜武等[16-17]利用ICA 方法,在地震信息处理中进行了初步的应用研究,发现该方法在地震信号特征提取与信号分离方面具有应用前景;吕文彪等[18]对ICA 方法进行了改进,利用两部特征值分解法去除噪声;李大卫等[19]为提高分离信号的质量,引入模拟退火算法,大幅度提高了地震资料的信噪比;张念等[20]对ICA 算法数学模型进行求解分析,并利用FastICA 算法对仿真地震信号进行了去噪测试;张银雪等[21]提出一种步长自适应ICA 算法,实现了对叠前地震信号的去噪;王维强等[22]利用EMD 对信号自适应分解的优点,结合ICA 算法,实现了随机噪声和有效信号的分离;袁星虎等[23]将五阶收敛速度的牛顿迭代式引进FastICA 算法,实现了对混合地震信号的分离;逯宇佳等[24]将ICA 算法与动态时间规整(DTW)算法相结合,实现了对非平缓地层中随机噪声的压制。
标准的ICA 模型要求观测信号数大于等于源信号数,且传统的ICA 算法是基于相同道或者相似道数据的多次观测,而实际地震资料通常是由成千上万的道记录组成,直接利用ICA 算法进行去噪,效果不一定理想。实际地震资料道数较多,每一道地震数据可以看成是一个独立的一维信号,如果针对每一道进行单独处理,则观测信号数小于源信号数,标准ICA 模型转化为一个欠定问题的求解,也就是从一个观测信号中分离出多个源信号。相空间重构是随混沌理论发展而来一种信号重构技术,是非线性动力学去噪方法的理论基础,被广泛应用于低维信号到多维信号的重构。根据Takens 嵌入定理[25],一维信号经过重构后可以转换到等价的多维相空间中,并可反映原始信号的系统动力学特征,其关键在于相空间重构参数(嵌入维数和时间延迟)的选取,准确地重构参数可以保证重构后的相空间能充分反映原始信号的动力学特征。重构参数选取的方法也比较多,在实际数据处理中,可以通过一个固定值来确定2 个参数,该固定值被称为时间窗,可以表示为:tw=(m-1)τ,其中m为嵌入维数,τ为时间延迟,通过一个参数的变化来确定另一个参数,从而确定最佳的2 个参数组合。然而,这2 个参数的选取不应该是相互独立的,而应该与时间窗有关,且随着时间窗的变化而变化[26]。1999 年Kim 等[27]提出了一种C-C 算法,该算法利用和嵌入维数有关的关联积分,并对其进行求解,可以同时确定这2 个重构参数,同时,该方法计算量相对较小,而且获得的结果也更为准确。
本文提出一种基于相空间重构的地震信号单通道盲源分离算法,来对地震资料进行处理。首先,利用C-C 算法确定信号的重构参数;然后,利用相空间重构技术将一维信号进行重构;最后,对重构后的高维信号利用ICA 算法结合数据自身的高阶统计特性,对有效信号和噪声进行分离,进而提取有效信号记录,从而达到保真去噪的目的,为后期精细解释提供质量更高的处理结果。。
1 方法原理
1.1 相空间重构
野外采集的地震信号一般是由有效信号和噪声2 个部分组成,因此,每一道地震信号也都可以看作是一个由噪声和有效信号组成的一维时间序列。针对每一道地震信号,利用ICA 算法进行处理是一个欠定问题(观测信号数小于源信号数),所以要对一维信号进行重构。本文采用相空间重构技术,将一维信号重构到高维的相空间中,相空间重构的过程可简单描述为:假设时间序列为x(ti),i=1,2,…,n,n为采样点数;令时间延迟为τ,嵌入维数为m,根据Takens 嵌入定理,则可以重构一个m维相空间:
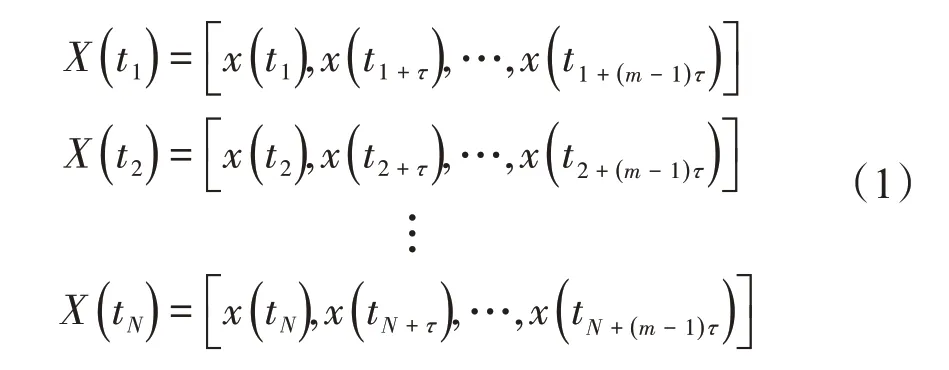
式中:X(·)表示相空间中的相点;N是相空间中的相点数,N=n-(m-1)τ。
1.2 重构参数选取
重构参数对相空间重构结果具有很大的影响,进而直接影响到最终去噪的效果。为了确定准确的重构参数,本文采用C-C 算法[27]对重构参数进行计算,计算过程可描述为
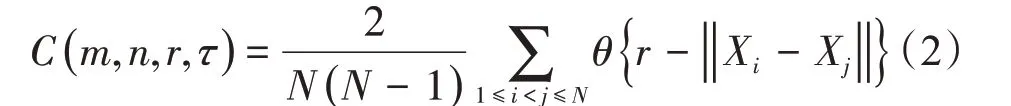
式中:C为定义的关联积分表达式;Xi为重构的相空间中第i个相点。
定义如下函数:
对时间序列进行不同划分来确定合适的时间延迟,具体的划分方法如下:实际观测的某一时间序列x={x1,x2,…,xn},当时间序列被划分为一个子序列,即t=1 时,划分后的时间序列就是该时间序列本身。

当t=2 时,原时间序列可被划分为{x1,x3,…,xn-1}和{x2,x4,…,xn} 2 个子序列,此时有
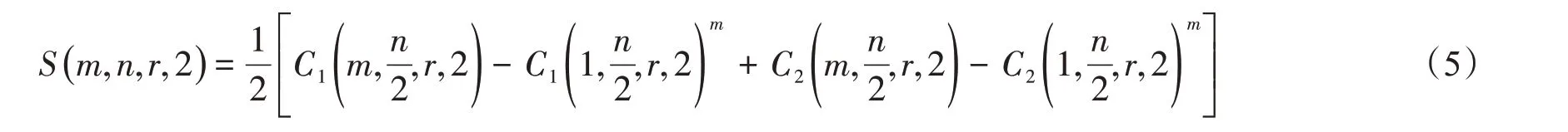
当时间序列被划分为t个子序列时,则有
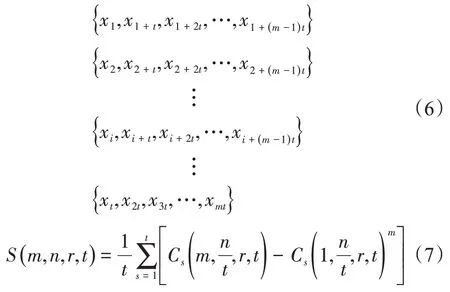
当n→∞时,
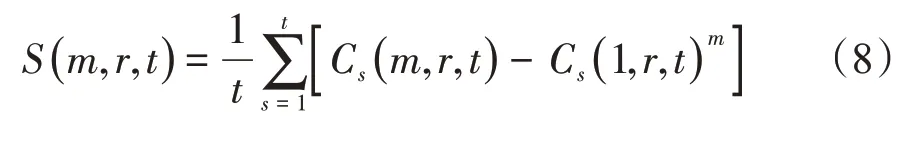
定义r对应最大值和最小值的差量:
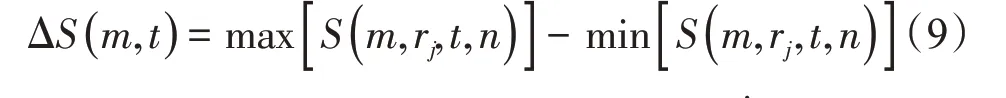
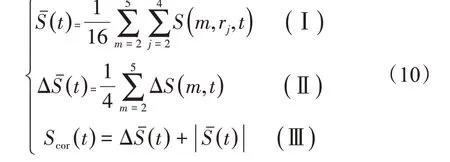
σ为时间序列的标准差,根据式(10),可以同时确定时间序列的重构参数,式(10-Ⅱ)的第一个极小值点的对应值就是所要选取的时间延迟值,根据式(10-Ⅲ)的最小值点可以确定对应的时间窗口,根据选取的时间延迟和确定的时间窗,利用公式tw=(m-1)τ,可以得到合适的嵌入维数值,进而将低维时间序列重构到高维相空间中。
1.3 独立分量分析
独立分量分析(ICA)算法是随盲源分析理论发展而来的一种独立源信号提取算法。该算法要求观测信号数,也就是待处理的信号数要大于源信号的个数,且源信号需相互独立,服从非高斯性分布。地震资料中的有效信号和随机噪声通常是相互独立的,另外,地震子波通常也是非高斯分布的。根据测井数据的统计结果可以得出,有效波的反射系数是超高斯分布的[28],地震信号是地层反射系数与地震子波褶积的结果。因此,地震信号恰好满足这一特点。所以,可以利用该算法对地震资料进行处理。
ICA 算法的去噪过程可以简单描述如下:
假设有n个独立的源信号可以表示为:S=[s1,s2,…,sn],通过一个混合矩阵A,A=[a1,a2,…,an]与S进行混合,可以得到混合后的观测信号X,其表示为
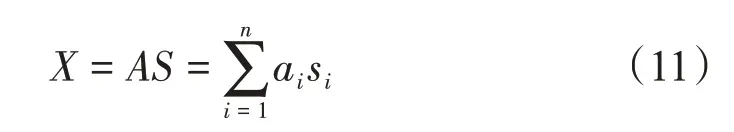
式(11)就是一个标准的ICA 模型,实际情况下,观测信号是已知的,混合矩阵和源信号是未知的。假设混合矩阵是一个可逆矩阵,那么,ICA 算法的本质就是求解一个分离矩阵W,也就是混合矩阵的逆矩阵,来实现对观测信号X的分离,得到分离信号
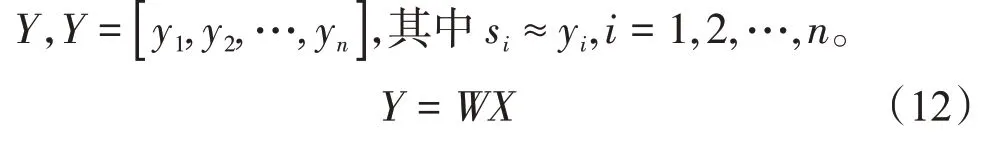
因此ICA 算法的核心就是分离矩阵的求取,在源信号和混合矩阵未知的情况下,首先对观测信号进行预处理包括白化和中心化,中心化的目的是使得每一个观测信号的均值为零,白化是指对经过中心化处理后的多维信号,通过一个变换矩阵进行线性变换处理,变为每个分量具有单位方差且互不相关的信号,对信号进行白化处理的目的是使分离算法收敛速度更快并且更稳定。
在求解分离矩阵时,选取负熵作为非高斯性的度量方式,可以表示为
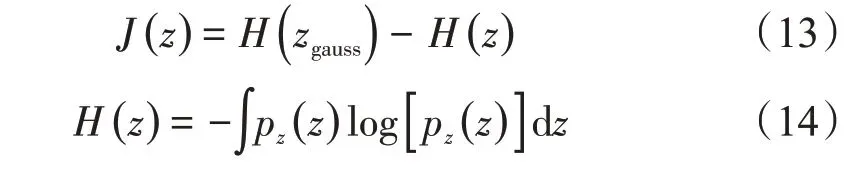
式中:z是经过白化和中心化预处理后的观测信号;zgauss为与矩阵z具有相同协方差矩阵的高斯随机向量;H(·)为随机变量的微分熵;pz(·)为随机变量的概率。
由于其不易求取,因此,式(13)和式(14)可分别变换为
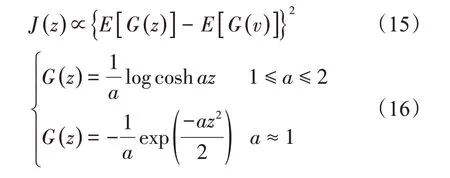
v是零均值、单位方差的高斯变量,G(·)的取值类型比较多,式(16)仅是其中的2 种,对不同类型的信号取值不同,对式(15)进行推导,可得到ICA算法的迭代式[20]为
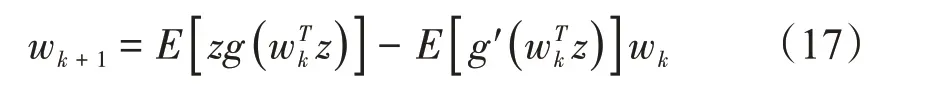
式中:g和g′分别是G(·)的一阶导数和二阶导数;w为分离矩阵W的行向量。
设定一个迭代终止条件和迭代次数,通过更新迭代求解得到所有的w,即得到最终要求的分离矩阵W。图1 是ICA 算法的处理流程图。
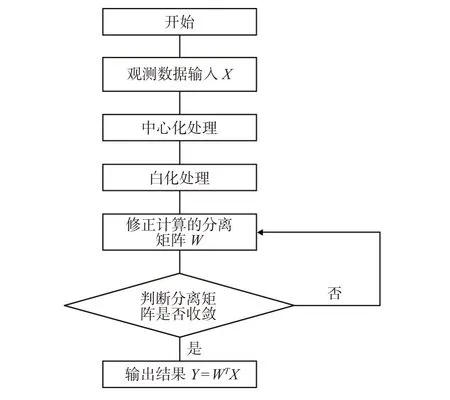
图1 ICA 算法流程图Fig.1 Workflow of ICA algorithm
1.4 基于相空间重构的地震信号盲源分离算法应用
利用本文方法对实际地震资料进行处理,整个处理过程可简单描述如下:
(1)针对每一道地震信号,利用C-C 算法计算信号的重构参数——嵌入维数和时间延迟;
(2)利用计算的重构参数,根据Takens 嵌入定理,利用相空间重构技术对地震信号进行重构,将一维信号重构到高维相空间中,从而满足ICA 算法的处理条件;
(3)对重构后的数据分别进行中心化和白化预处理;
(4)对预处理后的数据,利用ICA 算法进行信噪分离处理,最终得到分离后的噪声信号和有效信号,达到保真去噪的目的。
2 合成数据测试
为了验证本文方法的可行性,利用该方法分别对合成数据和实际数据进行处理,合成数据分为2个,一个简单的一维信号和一个简单的二维线性模型,一维合成信号[图2(a)]子波采用雷克子波,合成信号的采样点数为2 000 个,采样间隔为1 ms。对原始合成信号添加随机噪声[图2(b)],得到含噪的地震记录[图2(c)];然后,利用本文方法对含噪信号进行去噪处理,分别得到去噪后的有效信号[图2(d)]和去除的噪声[图2(e)]。

图2 单道合成数据测试Fig.2 Single channel synthetic data test
为得到较好的去噪效果,需要确定合适的重构参数,利用C-C 算法对单道含噪信号计算重构参数(图3)。图3(a)第一个极小值点对应的τ值为计算的时间延迟τ=5;通过图3(b)确定时间窗τw=15;利用时间延迟、嵌入维数以及时间窗三者之间的关系:tw=(m-1)τ,计算得到嵌入维数m=4。利用计算的重构参数,根据Takes 嵌入定理,可以对原信号进行相空间重构(图4)。
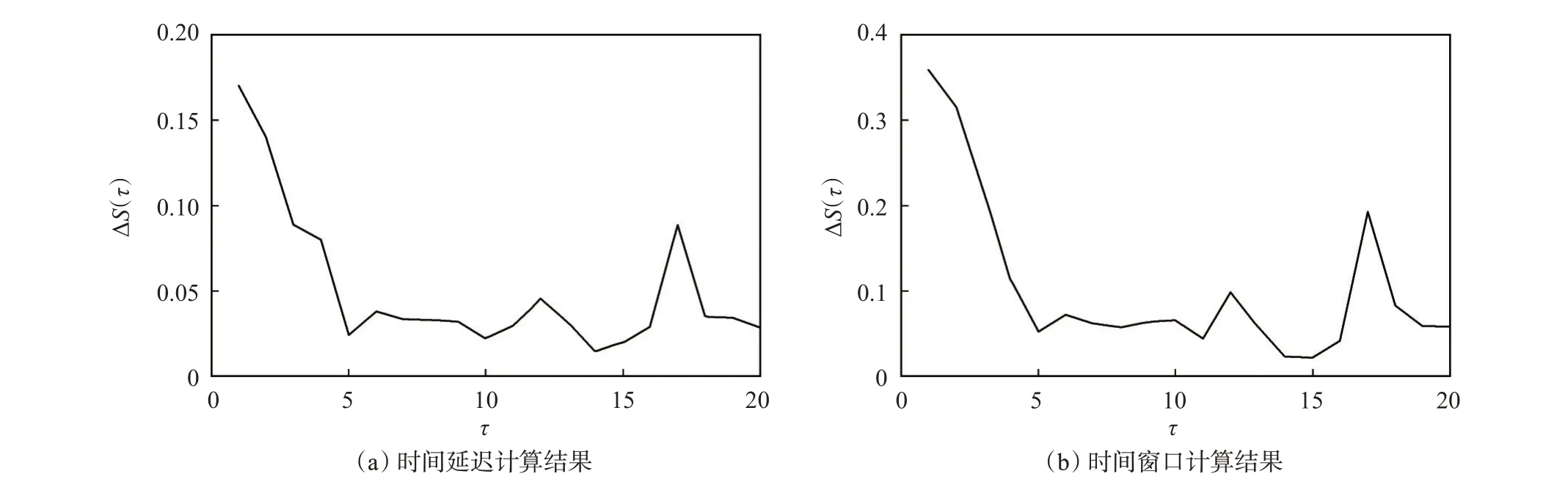
图3 C-C 算法计算结果Fig.3 Calculation results of C-C algorithm
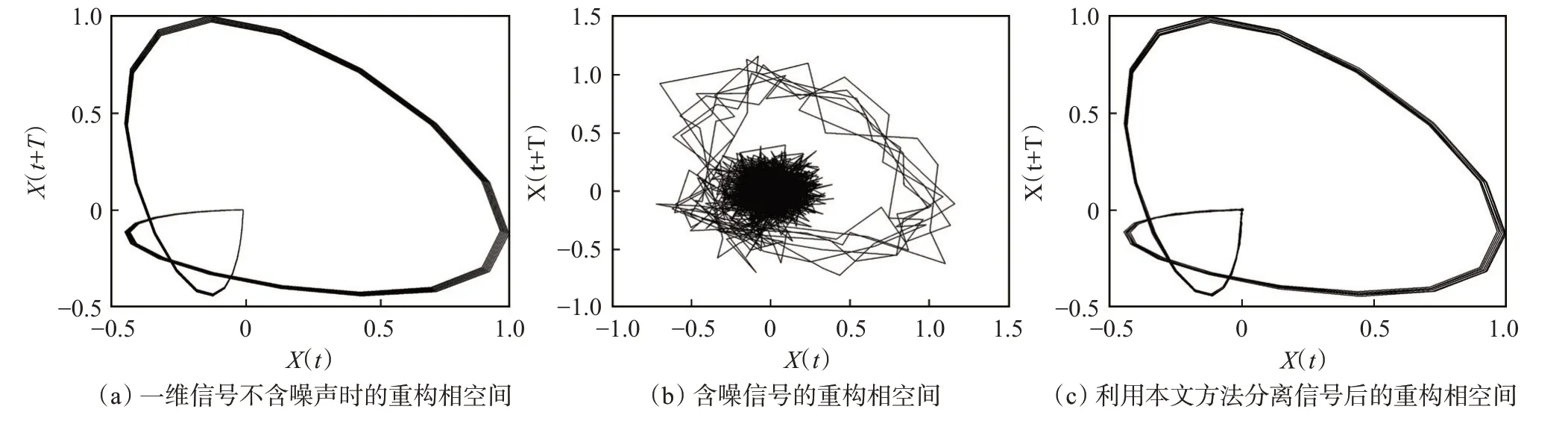
图4 相空间重构结果Fig.4 Result of phase space reconstruction
本文又利用二维线性模型进行去噪测试,二维线性模型如图5(a)所示,对该模型数据添加一定程度的噪声[图5(b)],然后,利用本文方法对含噪数据进行去噪处理,信噪分离结果分别如图5(c)和图5(d)所示。从分离的有效信号和噪声结果上可以看到,随机噪声得到了有效去除,有效信号更容易识别,资料的信噪比以及分辨率也得到了大幅度的提高。

图5 模拟数据去噪结果Fig.5 Denoising results of simulated data
3 实际资料处理
在实际资料处理中,随机噪声的去除方法也比较多。大多数去噪方法都是在资料具有一定的信噪比基础上进行随机噪声压制,而且在处理过程中,由于容易伤及有效信号,所以,针对随机噪声的压制一般都比较慎重,尤其是当资料信噪比较低时,有效地去除随机噪声更为困难。
本文选取四川盆地某地区三维资料的部分叠加剖面,从剖面整体来看,浅层噪声比较发育,部分噪声信号能量强[图6(a)]。利用f-xRNA 随机噪声压制方法对该资料进行处理后,叠加剖面上部分噪声得到了有效压制,信噪比较之前也得到了一定的改善[图6(b)],但是,还是可以明显看到部分异常噪声。使用本文方法进行处理后的效果相比RNA要更好一些,噪声去除相对更彻底,尤其是针对有效信号比较弱的浅层区域,经过处理后有效信号更加突出,资料信噪比、分辨率更高[图6(c)]。此外,从去除的噪声剖面[图6(d)]上来看,利用本文方法在消除噪声的同时,对有效信号几乎没有损伤。
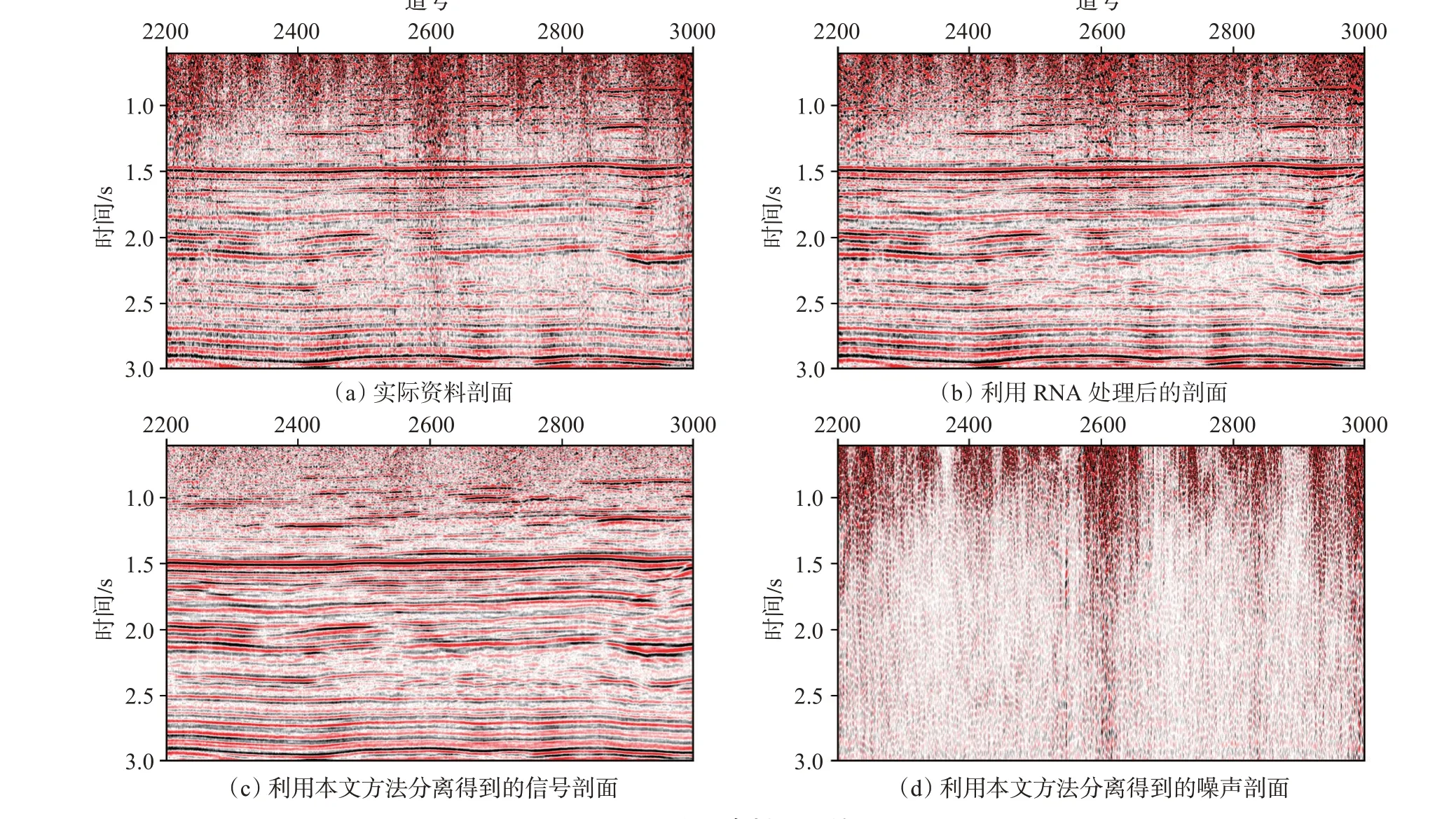
图6 实际资料处理结果Fig.6 Processing results of actual data
4 结论
(1)单通道盲源信号分离是一种欠定问题求解,已知信息较少,需要估计的未知因素比较多,本文基于相空间重构理论,可以将低维信号重构到高维相空间,进而满足多通道盲源分离算法的要求,易于求解。
(2)重构参数的选取对相空间重构具有重要影响,进而影响最终的信噪分离效果,本文采用C-C算法,根据信号自身的特征,可以准确地计算时间延迟和嵌入维数的值,进而为相空间重构提供准确合适的重构参数。
(3)根据重构相空间中噪声和有效信号重构轨道的几何特征差异,利用ICA 算法,结合数据自身的高阶统计特性,可以有效的实现信噪分离,合成数据和实际数据处理结果证明,该方法可以有效分离源信号,达到保真去噪的目的。
