基于模糊BP神经网络雷达导引头的性能评价∗
2021-08-08吕卫民胡文林
岳 炯 吕卫民 胡文林
(海军航空大学 烟台264001)
1 引言
20世纪六十年代,美国加州大学Zedeh在集合论的基础上研究了模糊数学处理方法[1],提出了模糊集、隶属函数、语言变量和模糊推理的概念,随后又提出了模糊逻辑理论的概念,首次将模糊理论和人工智能发展方向联系在一起。1992年第一届模糊系统的国际会议首次召开及专刊IEEE Transac⁃tion on Fuzzy system的创办[2],标志着模糊理论成为一个具有重要意义的新的研究领域。
模糊神经网络是将模糊系统和神经网络结合在一起,以神经网络为基础,利用模糊系统将各环节参数模糊化,将运算规则模糊化的新型算法。模糊神经网络有多种组合形式,目前应用较为广泛的是利用神经网络进行模糊逻辑推理,新的结合模型一方面具有模糊逻辑推理强大的结构表达能力,另一方面又具有神经网络强大的学习适应能力。
2 模糊系统
在经典集合理论中,两个集合的关系只有“属于”和“不属于”两种状态,但是在实际应用中,往往不会把界限划分的这么明显,比如:A的年收入比B多很多,这个“很多”表达的意思比较模糊,没有明确的定义界限,就是个模糊集合。1965年,美国加州大学Zedeh以集合论为基础研究了模糊数学处理方法,有效解决了模糊性事件的定量描述,创造师,研究方向:装备系统工程。胡文林,男,博士研究生,研究方向:系统工程。了模糊理论新的研究领域。
2.1 模糊集合和隶属函数
1)模糊集合。模糊集合是经典集合论的推广,在经典集合理论中,对两个集合之间的“属于”和“不属于”关系的特征函数描述只有“1”和“0”两个表达方式[3]。

Zedeh将经典集合理论中特征函数的取值范围由简单的数字集合{0 ,1}延伸到可连续取值的闭区间[0 ,1]。同时引入了模糊集的概念,记论域U中一模糊集为A,A的隶属函数为μA,μA(u)表示的是论域中元素u对模糊集A隶属程度的大小,两个模糊集相等则其分别对应的隶属函数也相等。
2)隶属函数。隶属函数如上所述,是表示与模糊集合接近程度的函数,反映事物走向的一个渐变过程,通过得到集合的隶属函数,能够对模糊集合进行定量分析[4]。在给定论域U上的一个模糊集合A用一个取值在[0,1]范围内的隶属函数μA(u)来表示,当u隶属A程度越大,μA(u)的取值越接近于1,当u隶属A程度越小,μA(u)取值越接近于0。即U隶属集合A的程度表示为

常见隶属函数主要有高斯函数和三角型隶属函数两种[5]。
(1)高斯函数[6]。高斯函数表达式为

(2)三角型隶属函数[7]。三角型隶属函数表达式为

2.2 模糊逻辑
在模糊集合中,对模糊概念或模糊性事物的描述语句称作模糊命题,模糊命题[8]是普通命题的推广,其运算法则同模糊集合运算类似。模糊命题是指具有模糊性的陈述句,通常用大写字母表示,将模糊命题转化成取值在[0 ,1]范围内的变量,其称之为模糊命题变量,通常用小写字母表示。设模糊命题X和Y,对应的真值分别为x=μA(X)和y=μA(Y),则x,y∈[0,1],
模糊命题的几种常见运算如下[9]:
1)X∧Y的真值x∧y=min(x,y);
2)X∨Y的真值x∨y=max(x,y);
4)X→Y的真值x→y=xˉ∨y。
2.3 模糊推理
模糊推理[10]是指在确定的模糊规则下,由已知的模糊命题推理出新的模糊命题的一个过程,模糊推理常用“If…,then…”形式,其中“If…”部分是前提,“then…”部分是结论。主要有广义前向推理和广义反向推理两种,广义前向推理是已知前提求结论,广义反向推理是已知结论求前提。
模糊推理的具体过程有以下步骤[11]:
1)模糊化。将输入量进行模糊化处理,换句话说就是将输入量转换成模糊集合,并求得隶属函数相对应模糊集合的隶属度,此步骤的模糊化主要分为非单值模糊化和单值模糊化两种方式。
2)规则库。是若干模糊控制规则的集合,大多以“if…then…”形式进行模糊条件判断,规则库主要是根据研究对象特征和相关领域内专家经验总结而成,对于一个已知规则的模糊条件可用模糊算子表示得到一个数值,数值表示模糊条件对于规则的匹配结果。
3)推理机。对每个规则赋予一个权值来进行模糊蕴涵,每个规则的蕴涵过程是给定一个单值作为输入,输出是一个模糊集合。
4)去模糊化。将聚类输出的模糊集作为输入,输出是一单值。
其推理过程如图1所示。

图1 模糊推理系统
3 模糊BP神经网络
模糊BP神经网络[12]是将模糊系统和BP神经网络系统有机结合的算法模型,这一模型同时兼具模糊系统知识结构表达能力和BP神经网络系统的自学适应性能力,目前这一算法在数据预测、综合评价、智能控制方面得到很好的应用。
模糊BP神经网络是在BP神经网络的结构基础上,将输入、输出、权值和学习算法等因素模糊化,将传递函数用模糊算子来代替,将“领域知识”用模糊集合来表示。模糊系统和BP神经网络具备一定关联性,原理基础是二者都是有基本神经元构成,拓扑结构相似,在理论上模糊系统能以任意精度逼近一个非线性函数,BP神经网络具有很强的映射能力,通过反复训练也能满足拟合精度要求,模糊系统可以处理显性逻辑问题,二者主要区别就是对网络结构中各项参数的描述不同。
模糊BP神经网络建立的设计思想是将模糊系统中的模糊化处理、模糊推理过程中模糊规则和隶属函数用神经网络来表示,利用神经网络算法提高模糊系统精度。模糊神经网络可以说是一种改进型神经网络,在具有自学自适应功能的同时,也具备了模糊推理功能,从而进一步增强了神经网络的透明度和解释能力。在构建模糊神经网络前,对各层节点的确定和优化十分重要。第一层输入层节点数是由研究对象系统的输出数,设节点数为m;第二层模糊化层、第三层规则层和第四层归一化层的节点数一致,设为n;五层是输出层。

图2 模糊BP神经网络模型
第一层:输入层。节点直接与输入变量相连并由输入层输至下层,可表示为

第二层:模糊化层。模糊化层的作用是将输入层的输入变量模糊化,然后再定义模糊子集,通过各模糊子集的隶属函数,将输入变量转化成对应模糊子集的隶属度[13],下面隶属函数用高斯函数来表示。
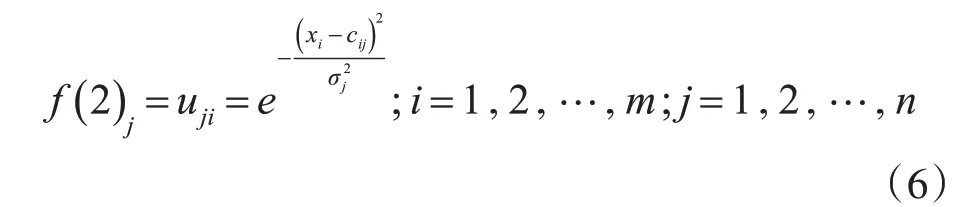
其中cij表示第i输入节点模糊化层中第j个模糊子集隶属函数的中心值,σj是模糊化层第j个模糊子集隶属函数的宽度。
第三层:规则层。该层的输出为各节点所有输入信号的乘积,即规则层是用于匹配模糊化处理过的数据和模糊规则。
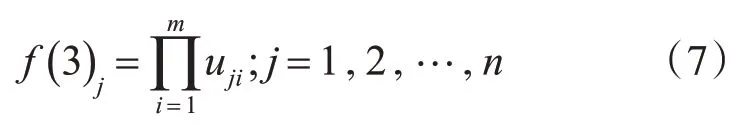
第四层:归一层。将每个规则层输出的模糊子集归一化处理成一个单独的模糊集。

第五层:输出层。将规则层的输出进行反模糊处理,最后得到整个模型的输出值。

其中ωji是归一层到输出层各模糊集合模糊集合的连接权值。
对于模糊BP神经网络模型,利用BP神经网络对模糊隶属函数的参数cij、σj和输出层连接权值ωji进行训练调节,以达到逼近模型输入输出明确的函数关系的目的。设模型的期望输出为Fj,实际输出为oj,模型的输出函数记作Ej,则可得到如下关系式:
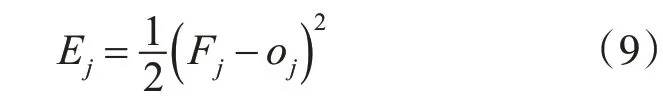
则上述三个参数的调整为

其中η是学习率,i=1,2,…,m;j=1,2,…,n。
4 模糊BP神经网络的改进
利用BP神经网络在反向转播过程中利用误差不断修正连接权值阈值的功能,对模糊隶属函数的参数cij、σj和输出层连接权值ωji进行调节。

与常规权值调整公式中常数项动量因子α0不同,改进后的动量因子是一个变量,其取值受前面输出误差的影响,且大小随输出误差比值大小做调整。按照经验可知,α0∈( )0,1,误差调整总体呈下降趋势。现令

则参数cij、σj和ωji调整为
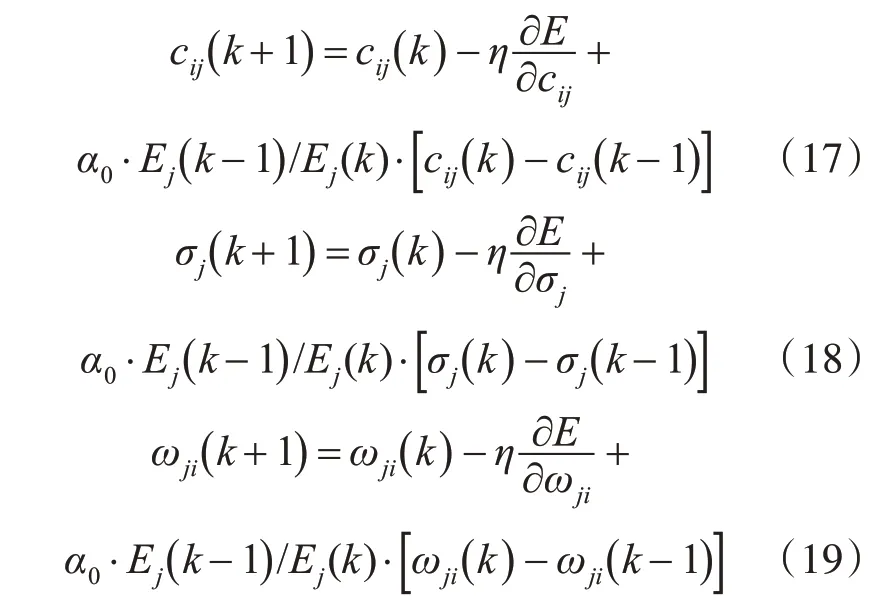
此外,学习速率η的取值对网络的训练性能也同样有一定影响,通常为一常数。η取值过小,会延长训练时间,训练收敛减慢;η取值过大,对网络稳定性降低起一定作用。综合考虑训练时间和稳定性两方面因素,参照预先设定的误差参数,提出对η取值进行调整,当网络输出误差较上一层输出超出设定值,则减小η值,反之增加,直至网络训练收敛达到预期。η取值如下:

通过自动调整η来实现始终以最大允许速率对网络进行训练。
5 实例应用
某型防空导弹系统是目前我国正在服役的主要防空武器系统之一,具有精度高、覆盖面广和机动性强等特点。该型导弹雷达导引头是整个导弹的重要部件,其工作性能的好坏直接影响整个导弹的战斗效能。导引头故障发生有多种影响因素导致,这些因素和故障的发生很难有明确的数学表达式来表示,故障和影响因素之间往往呈现模糊性和随机性特征。
导引头的性能检测主要是电测检测,主要检测对象是导引头各部件,所测量参数主要选择磁流管电流、电源电压、自动功率调节值、跟踪性能参数,用四个性能参数来进行导引头性能状态的评价。下面根据2013~2017年各季度对该型雷达导引头的各项性能参数测试数据来对导引头2018年性能状态进行预测评价。
1)输入层参数
记输入层各参数集合磁流管电流I、电源电压U、自动功率调节值P、跟踪性能参数Q。
将各测量参数进行归一化处理:

其中xmax和xmin分别代表四个检测参数在相应指标取值范围内的最大值和最小值。则各参数输入在[0,1]区间取值。
2)隶属函数选取
每个输入量都有各自的隶属函数,并产生多个模糊规则,三角型隶属函数适用于解决线性问题,但导引头故障发生多数属于累计失效,呈非线性函数关系,将各输入量对应的隶属函数选择为高斯隶属函数。

3)模型建立及训练
按照四项指标参数变化情况对导引头整体性能状态影响大小来对四项指标进行权重赋值,根据经验数据总结,四个参数权重取值分别为0.29、0.19、0.30、0.22,将各性能参数加权后生成导引头性能完好率作为模糊BP神经网络的输出。根据导引头被测性能参数特点,确定模型输入节点数为4,输出节点数为1,中间层节点的选择对网络精度和由经验公式(r取1~10)可得,中间层节点数选7。设网络训练次数为1500,训练目标0.0001,各参数权值wji的初始取值分别为0.29,0.0152,将训练输出与实际数据作对比,当误差在允许范围内,则训练结束,否则不断调整隶属函数参数,直至达到理想输出。下面利用实测数据对改进前后模型进行训练,并对比两模型训练收敛速率大小。
由图3可见,改进后的模糊BP神经网络训练速率要比传统模糊BP神经网络快。
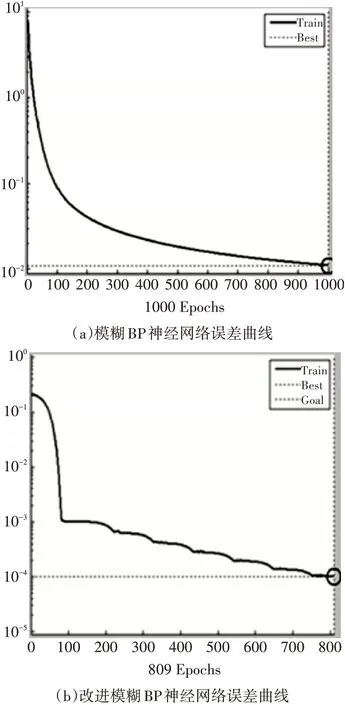
图3 改进前后模糊BP神经网络训练收敛速率曲线
4)导引头性能状态的预测
利用改进模糊BP神经网络对隶属函数各参数进行调整训练。观察改进前后模糊BP神经网络的运算速度和预测精度,对2018年导引头性能状态预测见表2。

表2 改进前后FNN模型预测数据及误差表

表1 导引头各参数实测数据及性能评价表(2013年~2017年)
由图3和表2可见,改进后的模糊BP神经网络在运算速率和预测误差都比改进前的模型有一定程度的提高,说明改进后模糊BP神经网络在导引头性能状态预测方面有更好的适用。但是从效果上来看,运算速率和预测精度的改进效果都不太明显,这可能取决于模糊推理系统和BP神经网络的融合程度,需要进一步论证。
6 结语
本文在传统模糊系统和BP神经网络的基础上将两种算法结合成新的组合模型,并在组合模型的基础上,通过调整BP神经网络结构中的动量因子和学习速率的重新赋值来调整模糊系统中隶属函数的取值。改进后的模糊BP神经网络模型兼具两种算法的优点,且在理论上收敛速度更快,运算精度更高。根据雷达导引头性能评价实测数据,通过运算仿真实验表明,改进后的模糊BP神经网络训练收敛速率更快,误差精度也有一定程度的提高,从而证明改进模糊BP神经网络模型对导引头性能状态评价具有很好的适用性。
