热浮力对球床反应堆内燃料球表面对流传热的影响

姚强 郭雪岩 杨帆

摘要：采用大涡模拟（LES ）方法研究了低雷诺数（Re =1015）下热浮力对球床面心立方（FCC ）单元内的局部流动和传热的影响。为了精确求解燃料球接触面附近的流场，球间接触点表达为面接触，采用结构化网格处理。研究结果表明：热浮力的存在会抑制球床各层平均速度的波动;靠近燃料球表面处的相对时均速度和相对时均温度受热浮力影响变化较大;在中心流场区域，热浮力的存在会减小流场中速度分布的不对称性，使速度最大降低约10%，时均温度至少升高约20%;球表面上尤其在顶部及接触面附近受热浮力影响明显，努塞尔数 Nu最大降低约6%。

关键词：热浮力;球床反应堆;大涡模拟;面心立方;面接触

中图分类号： TK11+2    文献标志码： A

Effect of thermal buoyancy on the convective heat transfer on the surface of fuel pebbles in a pebble bed reactor

YAO Qiang，GUO Xueyan，YANG Fan

（School of Energy and Power Engineering， University of Shanghai for Science and Technology， Shanghai 200093， China）

Abstract：In this paper， large eddy simulation （LES） method was adopted to study the influence of thermal buoyancy at low Reynolds number （Re =1015） on local flow and heat transfer in a face- centered cubic （FCC） of a pebble bed. The plane-plane contact among the pebbles and structured grid were adopted to accurately solve the flow field near the interface of fuel pebbles. It is found that the existence of thermal buoyancy could restrain the fluctuation of averaged velocity at each layer. The influence of thermal buoyancy on relative time-averaged velocity and relative time-

averaged temperature near the surface of fuel pebbles was great. In the center of flow field， the existence of thermal buoyancy could reduce the asymmetry of velocity distribution. The velocity decreased by 10% at most and the time-averaged temperature increased by 20% at least. On the spherical  surface，  especially  at  the  top  and  near  the  interface，  obvious  influence  of thermalbuoyancy was observed. And the Nusselt number Nu number decreased by 6% at most.

Keywords：thermal buoyancy; pebble bed reactor; large eddy simulation; face-centered cubic; plane-plane contact

球床式高溫气冷堆是第四代核反应堆类型之一。在球床反应堆中，氦气作为冷却剂，核燃料嵌在石墨慢化剂中并可以维持很高的温度。这种结构可以保证燃料不会熔化，使反应堆具有良好的固有安全性[1–4]。该堆型具有结构简单、燃料元件适合批量生产以及燃料球装卸方便等特点。

目前，很多学者对球床中的流动和换热特点进行了研究。孟现柯等[5]用由碳钢球堆积成球床，以蒸馏水为工质，采用电磁感应加热方式研究了球床通道内部的换热特性; Jia 等[6]用黑色玻璃球堆积成球床，以水为工质研究了不同床型对内部工质流动情况的影响。考虑到实验成本和复杂性，多数实验结果很难为球床反应堆提供可靠的参考依据。Lee 等[7]于2007年采用k 一"湍流模型比较了不同球间间隙对流场分布的影响;2014年，Ferng等[8]用雷诺应力湍流模型、非结构网格对体心立方（ BCC ）人工间隙和点接触两种接触方式的共轭模型的模拟结果进行了分析比较;2012—2015年， Shams 等[9–11]采用 q?DNS 方法、多面体网格对面心立方（FCC ）人工间隙模型进行了分析，发现在两球之间的狭窄区域存在射流现象及速度场、温度场分布的不对称性;2017年，蒋旭等[12]采用大涡模拟（ LES ）方法、结构网格研究了 BCC堆积模型的流场和温度场，通过与k一"湍流模型计算结果对比发现，采用 LES 方法能够更好地捕捉流场中的涡结构，瞬时温度变化更具参考价值。采用数值方法可以更容易获得更多的流场、温度场的信息，但多数学者采用数值方法时均只考虑球床在强制对流情况下的流动传热特性，而忽略了热浮力的影响。 Huang 等[13]对矩形腔内湍流混合对流特性进行了实验和数值研究，分析了浮力的影响，通过与实验结果进行对比，确定了 LES 方法在混合对流计算中的精度;Guardo等[14–15]采用数值方法，对随机球床内超临界二氧化碳在高压下的混合对流传质进行了分析，研究表明，对于层流状态下的超临界流体，可以直观地看到流量和流动方向对传质量的影响，在助流状态下，会得到更大的传质量。研究表明，混合对流中浮力的影响不可忽略，但对球床内流动和传热的研究还不够充分。

本文将采用 LES 方法、结构网格研究热浮力对球床反应堆内 FCC 面接触单元的燃料球表面及局部流动与传热的影响。

1几何模型与数值方法

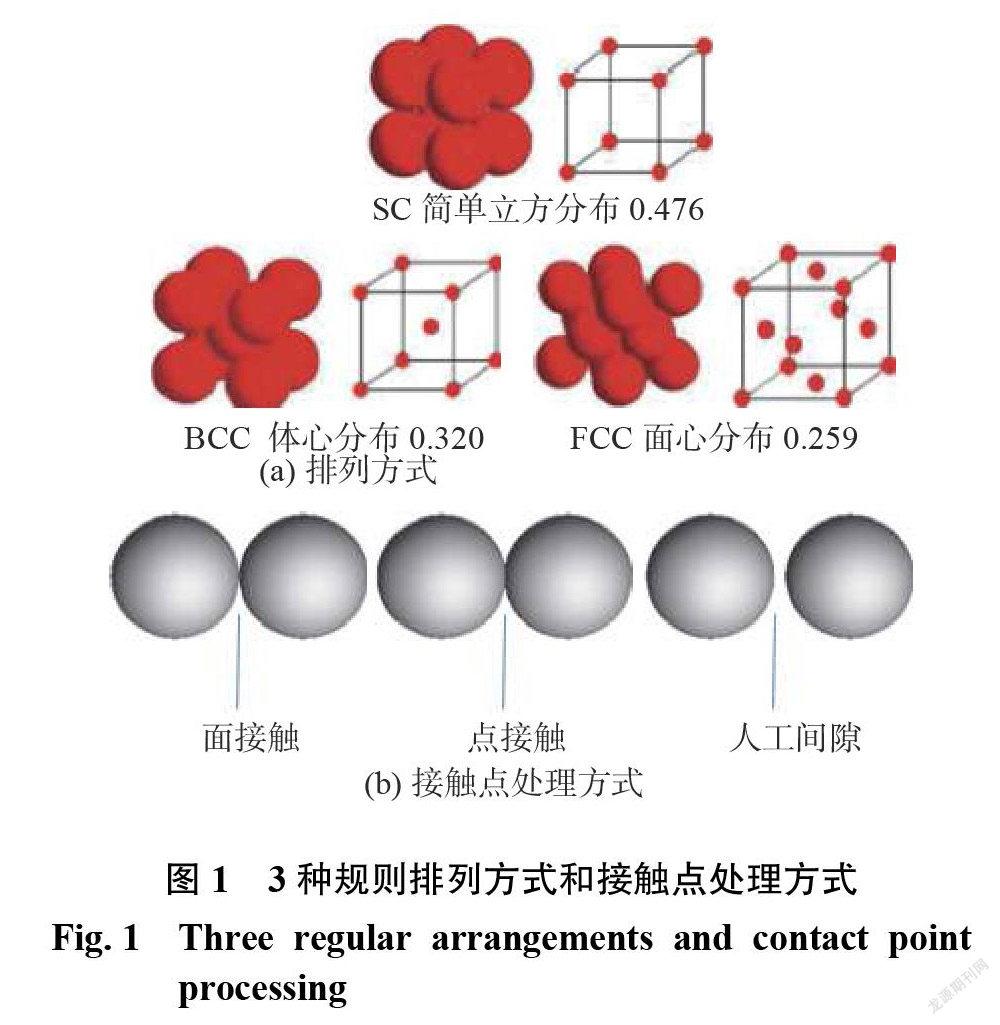
球的规则排列方式主要有3种[16]：简单立方（ SC ），体心立方（ BCC ），面心立方（FCC ）。球床内部燃料球堆积结构可以看作是3种方式的随机组合。两球的接触点一般有3种处理方式：人工间隙、点接触、面接触。3种规则排列方式和接触点处理方式如图1所示。由于3种排列方式中 FCC 结构空隙率最小，而实际球床中燃料球的无规则堆积必然使球床的空隙率最小化，因此本文选择燃料球的 FCC 排列方式，又考虑到两球在接触位置会存在一定程度的变形，对接触点的处理方式选择了面接触，由此得到了一个 FCC 单元。考虑到计算资源有限及为避免受进、出口效应影响，本文中采用4个 FCC 单元堆积模型，几何模型如图2所示。主要参数参考 Shams 等[11]中的值。燃料球球面材料为石墨，直径为60 mm，接触变形部分是燃料球直径的1%，内部冷却工质为氦气。边界条件及参数、物性参数分别如表1、2所示。

考虑热浮力时，密度采用Boussinesq近似，计算 Gr/Re2= g*αv?tl/v2=0.024，其中： g*为本文中采用的重力加速度， g*= gαv（ Tmax一Tmin），Tmax和Tmin分别为;αv为体积膨胀系数;?t为进、出口温差;l为特征长度;v为流体进口速度; Gr 为格拉晓夫数;Re 为雷诺数。复合对流中，采用Gr/Re2作为判断自然对流影响程度的判据。一般认为，当Gr/Re2≥0.01时，自然对流的影响不能忽略。本文中重力方向与流动方向相同，热浮力方向与流动方向相反。

为了能够捕捉更多的瞬时流场信息，采用 LES 方法进行研究。亚格子模型采用动态Smagorinsky?Lily 模型，其优点在于具有一定的自适应性，得出的结果更可靠。

2网格适用性验证

为了提高计算结果的准确性，对所采用的 FCC 面接触模型进行结构网格创建，采用 ICEM 软件将流场区域划分成多个六面体几何结构并建立对应的六面体块，最后通过将几何体与对应的六面体块进行关联，成功完成了结构网格的划分，并对近壁面网格进行了加密。 FCC 面接触单元网格如图3所示。

为了验证近壁面网格加密方法的适用性，对 Shams 等[12]采用的 FCC 人工间隙模型，采用相同的结构网格划分方法进行全结构化网格的划分。在相同的边界条件和进、出口参数条件下，采用 LES 方法进行计算，获取了在垂直来流方向上近球面到中心流场区域的时均速度分布。图4为近壁面加密网格适用性验证结果。4（a）为提取数据位置。图4（ b）为 LES 和 q?DNS 方法结果对比，其中，横坐标表示的位置与纵坐标表示的时均速度都进行了无量纲化，并与 Shams等[14]的 q?DNS 数据进行对比;为时均速度， U为时均速度，Umax为最大时均速度;（Z 一Zmid）为在中心流场区域所提取线上的数据点 Z 相对中间位置Zmid的坐标;D 为燃料球直径。结果显示，与近球面处计算结果高度一致，由此说明近壁面的网格加密方法适用于该球床模型的数值计算。

为验证网格无关性，分别对网格数为720万、503万、325万的模型进行了计算，并整理对比了进、出口速度，温度差。以720万网格下的计算结果为标准，计算出另外两种网格数下得到的数据误差。网格無关性验证结果如表3所示，结果显示3种网格数的计算结果无明显差异，这说明325万网格已可满足计算要求，

网格数的增加对计算结果无明显影响。由于采用了 LES 方法，为了能更好地捕捉内部流场信息，本文中用于计算的网格数取为503万。

3计算结果与分析

在所研究的流场区域沿流动方向取相同的截面，获取截面上的平均速度，各层截面位置及平均速度、温度变化如图5所示。结果显示，在进、出口处速度变化较大，存在明显的进、出口效应，扰动较为剧烈。进口处受影响的程度相对较大，并持续到第3层截面之后。从第4层截面开始，流速呈现对称性波动，表明流动已基本稳定。可以发现，自第4层截面之后，热浮力影响效果明显，受热浮力影响的流体流速相对较低，说明热浮力的存在对流速起到抑制作用。第2层截面之后，每层温度均有升高，相邻两层温差ΔT 为7 K。为了进一步研究流场内部的流动和传热情况，通过以上的分析，选取第5层和第7层截面之间的 FCC 单元作为流场研究区域，选取3号中心球分析球面换热情况。

3.1热浮力对速度和温度场的影响

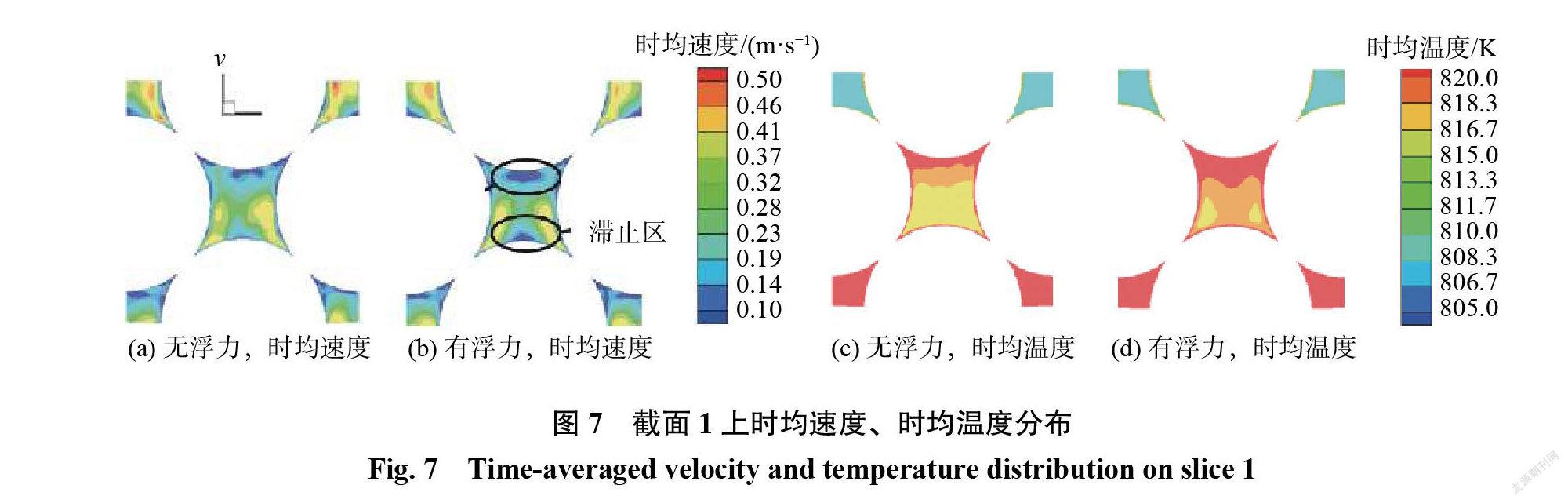
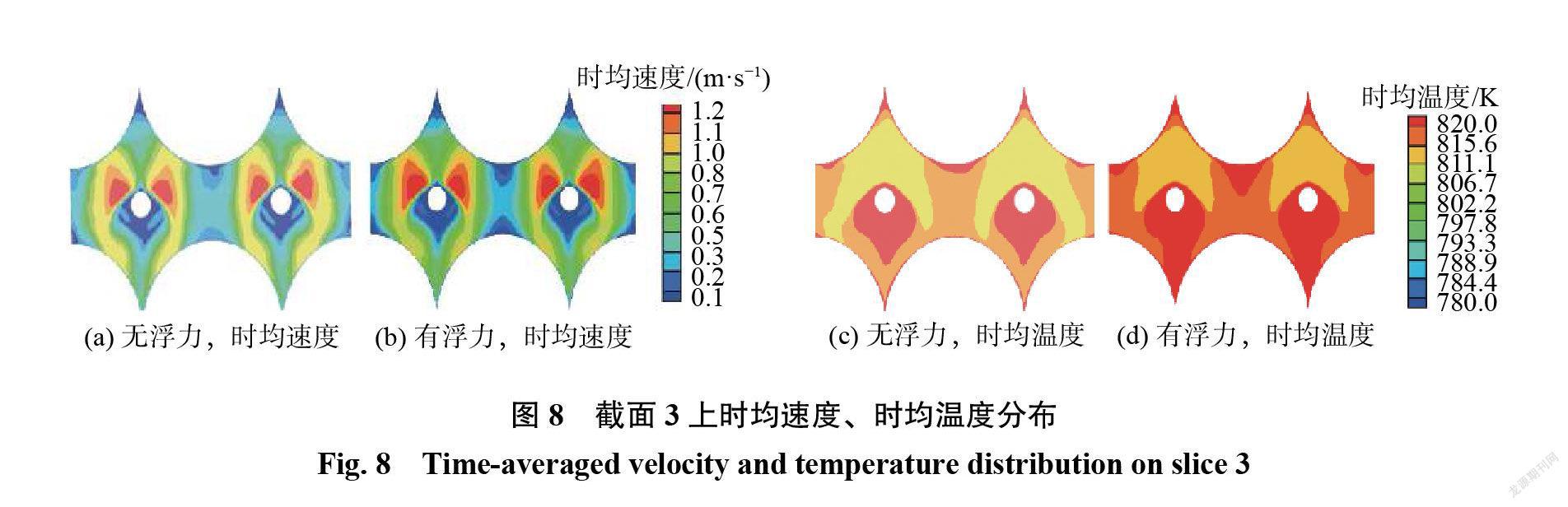
在所研究的 FCC 单元内选取截面1、2、3，流场区域各截面位置及截面上流线图如图6所示。获取截面1、3上的时均速度和时均温度分布，结果如图7、8所示。可以发现热浮力对局部流场速度与温度分布影响较为明显。在截面1的速度场中，受热浮力影响，低速区域增大，尤其在燃料球底部和顶部对应的尾流区和滞止区位置，低速区域明显增大。温度场中，低速区域的增大使高温区域随之增大，且在中心区域，尾流区温度较高。截面3与接触面相切，对比速度分布，在尾流区和滞止区同样可以发现与截面1中相同的现象。在接触面处热浮力存在时，流体速度会在发生分离的位置略微增加，之后的速度都会相对减小。截面上的平均温度相对较高，接触面处较为明显，高温区域延伸较长。这再次说明热浮力的存在对流速起到抑制作用。

为了解速度和温度在球面和中心流场区域之间的变化情况，在截面1上中心区域沿流动方向和垂直流动方向各取一条截线，如图9所示。提取线上的时均速度和时均温度分布，并与不考虑热浮力的分布进行了对比，结果如图10所示，其中：Vb、Tb 分别为考虑热浮力时的时均速度和时均温度;Vn、Tn 分别为不考虑热浮力时的时均速度和时均温度。分析截线1上提取到的时均速度和温度分布（相对于中心点）：沿 X 正方向，在近球面位置热浮力对速度和温度的影响并不明显;远离球面后，热浮力的影响开始增强。在热浮力影响下，相对中心点的对称位置处较低的速度被提高，较高的速度被降低，最终减少了速度分布的不对称性，也同样减少了温度分布的不对称性，截线上的温度有所提高，考虑到速度差的减小，降低了湍流强度，削弱了换热。相对于不考虑热浮力的情况，靠近球面位置，速度和温度的相对变化较大（速度最大降低70%，相对层间温差，温度最大增加43%）。远离球面后速度和温度相对变化趋于平缓，在中心流场区域速度相对变化范围在10%以内，温度平均增加约20%。

分析截线2上提取到的时均速度分布，沿 Y 负方向（流动方向），不考虑热浮力时，由上一个中心球底部到下一个中心球顶部，速度先快速增大，后缓慢增大，在中间偏下的位置达到峰值，后缓慢减少，至靠近球面位置急剧降低最后接近滞止，速度受滞止区和尾流区影响明显。在考虑热浮力后，由速度分布可以明显发现，相对中心点呈良好的对称性，截线上速度相对减小，峰值位置更靠近中心点。靠近球面处速度剧变的情况有所缓和，从一定程度上减少了由于速度变化大引起的湍流强度。从时均温度分布可以发现，考虑热浮力后，高低温差减小，中心区域截线上平均温度有所增加。靠近球面位置，时均速度和温度的相对变化较大，速度几乎滞止（相对层间温差，温度最大增加50%）。靠近中心流场区域，速度和温度的相对变化有所减小，温度最少升高约20%。

3.2热浮力对燃料球表面对流换热的影响

图11为3号中心球表面温度分布。由图中可见，热浮力的存在使球面部分位置温度相对升高，尤其在燃料球的顶部、侧面的4个接触面中间部分以及底部较为明显。本文中定义努塞尔数 Nu = hD/λ，h = q/（T 一 Tin），其中：h为对流换热系数;λ为氦气热导率;q为热流密度;T为球面上不同位置温度; Tin为氦气进口温度。球面Nu 分布如图12所示。对比发现，热浮力存在时，燃料球顶部及接触面附近的 Nu 明显降低，高 Nu 区域明显减小，且差异较明显的位置分布在燃料球的上半球面。由时均速度分布情况，顶部附近流场速度相对减小，减弱了对流换热，使局部 Nu 降低。由图6截面1、2、3上流线图可以发现，流场中的涡多集中在接触面后沿及燃料球底部的尾流区域，扰动较为剧烈。这说明热浮力的存在削弱了换热强度，而涡的存在增强了局部扰动，削弱了热浮力的影响。

为进一步了解顶部和接触面附近的换热情况，在球面上3个特殊位置取3条截线，截线3、4、5，取线位置如图13所示。球面3条截线上 Nu 分布如图14所示。通过对比每条截线上的 Nu分布可以发现，球面顶部换热最好，接触面附近由于接触面的阻碍作用 Nu较小，换热较差。在考虑热浮力的情况下，球面相同位置的 Nu 会相对减少，最大差值约为球面平均 Nu 的6%，即热浮力的存在對对流换热起到抑制作用。沿流动方向，位于球面不同位置，热浮力影响的程度也有所不同。由图中可以看出，燃料球的上半部分受热浮力的影响较大，而下半部分由于流体扰动较强受热浮力影响较小，这与分析球面 Nu 分布的结果一致。

4结论

采用 LES 方法，在考虑热浮力的情况下，对球床反应堆 FCC 面接触结构内的流动和传热进行了研究。通过对比分析整个球床各层的平均速度变化，局部流场中速度、温度场的分布及中心燃料球表面的温度、Nu 分布，得到热浮力对球床反应堆局部流动和传热影响的几点规律：

（1）低雷诺数下热浮力的影响不能忽略，热浮力的存在对球床中各层平均速度变化起到阻碍作用，会抑制速度产生较大的波动。

（2）在局部流场区域，时均速度、时均温度受热浮力影响明显。靠近球面位置，相对时均速度和相对时均温度变化较大。在中心区域，热浮力的存在会减小流场中速度分布的不对称性，速度最大降低约10%，时均温度最少升高约20%。

（3）相对来流方向，燃料球上半部分，尤其在燃料球顶部及接触面附近，受热浮力影响 Nu 减小，最大降低6%，削弱了换热。流体流过接触面接近球底部，涡结构增加，扰动剧烈，削弱了热浮力影响。

参考文献：

[1] 雷鸣泽.高温气冷堆产业推广及应用前景[J].中国核电， 2018， 11（1）：26-29.

[2]吴宗鑫. 我国高温气冷堆的发展 [J]. 核动力工程， 2000， 21（1）：39 - 43，80

[3] 符晓铭， 王捷.高温气冷堆在我国的发展综述[J].现代电力， 2006， 23（5）：70-75.

[4] 吴宗鑫， 肖宏才.模块式高温气冷堆的安全特性[J].高技术通讯， 1994（11）：34-38.

[5] 孟现珂， 孙中宁， 徐广展，等.含内热源堆积球床对流换热特性的实验研究[J].哈尔滨工程大学学报， 2012， 33（9）：1122-1126.

[6] JIA X L， GUI N， YANG X T， et al. Experimental studyof flow field characteristics on bed configurations in thepebble bed reactor[J]. Annalsof Nuclear Energy， 2017， 102：1-10.

[7] LEE  JJ，  PARK  G  C，  KIM  K  Y，  et  al. Numericaltreatment of pebble contact in the flow and heat transferanalysis  of  a  pebble  bed  reactor  core[J]. Nuclear Engineering and Design， 2007， 237（22）：2183-2196.

[8] FERNG Y M， LIN K Y. CFD investigation of thermal-hydraulic characteristics in a PBR core using differentcontact  treatments  between  pebbles[J]. Annals  of Nuclear Energy， 2014， 72：156-165.

[9] SHAMS  A，  ROELOFS  F，  KOMEN  E  M  J，  et  al.Optimization of a pebble bed configuration for quasi-direct numerical simulation[J]. Nuclear Engineeringand Design， 2012， 242：331-340.

[10] SHAMS A， ROELOFS F， KOMEN E M J. Quasi-directnumerical simulation of a pebble bed configuration. PartⅠ： flow （velocity） field  analysis[J]. Nuclear EngineeringandDesign， 2013， 263：473-489.

[11] SHAMS  A，  ROELOFS  F，  KOMEN  E  M  J，  et  al.Numerical  simulation  of  nuclear  pebble  bedconfigurations[J]. Nuclear Engineering and Design， 2015， 290：51-64.

[12]蔣旭， 郭雪岩.球床反应堆流动与传热的 CFD 分析：燃料球尺度[J].能源工程， 2017（6）：8-13，19.

[13] HUANG  YY，  YANG  G，  WU  J  Y. Large  eddysimulation and experimental study of turbulent mixedconvection inside a cavity with large Rayleigh number：effect of buoyancy[J]. BuildingandEnvironment， 2019， 151：268-279.

[14] GUARDO A， COUSSIRAT M， RECASENS F， et al.CFD study on particle-to-fluid heat transfer in fixed bedreactors： convective  heat  transfer  at  low  and  highpressure[J]. Chemical  Engineering  Science， 2006， 61（13）：4341-4353.

[15] GUARDO A， COUSSIRAT M， RECASENS F， et al.CFD studies on particle-to-fluid mass and heat transferin packed beds： free convection effects in supercriticalfluids[J]. Chemical Engineering Science， 2007， 62（18-20）：5503-5511.

[16] OOMS A. Pebble flow in a high temperature reactor[R].Physics  of Nuclear  Reactor. PNR-131-2008-003. TU Delft， The Netherlands， 2008.