预应力锚索的张拉次序对闸墩应力及变形的影响研究

王己海，费文平

（1.四川大学水力学与山区河流开发保护国家重点实验室，成都610065；2.四川大学水利水电学院，成都610065）

0 引 言

预应力闸墩是保证大型泄水建筑物安全的重要结构，这种采用预应力锚索与闸墩结合的技术能够有效改善闸墩的应力状态，确保在弧门推力的作用下闸墩结构的安全可靠。在预应力锚索与水推力的共同作用下，闸墩结构的应力与变形状态变得更加复杂，很难从理论上对应力与变形进行计算分析，而对预应力锚索影响闸墩应力与变形的可能因素成为了主要的研究方向。

多年以来，国内外的学者与工程师对改善预应力闸墩的应力与变形的可能因素做了许多研究，并取得了一定的成果。国际上，预应力闸墩最早在20 世纪50年代末期应用于突尼斯的梅列格溢洪道上。在20 世纪60年代，美国在哥伦比亚河修建瓦那庞溢洪道工程时，采用了14束每束张拉力为2 900 kN 的锚索锚固［1］。随着有限元方法及计算机技术的发展，数值模拟技术得到了迅猛发展，国际上出现大量的商业数值模拟软件。其中较为著名的通用大型有限元软件有ANSYS、ABAQUS、MSC.NASTRAN 和MSC.MARC 等［2-4］。在国内，在闸墩结构优化方面，朱暾等［5］提出了闸墩颈部开槽结构，该型式可以显著提高混凝土的抗裂能力，改善闸墩的应力分布状态；胥润生［6］提出“深槽+锚孔”的结构方式，大大节省了锚索数量，优化了施工步骤；中国水电院提出了一种新的简支传力梁结构，使锚索预应力通过传力梁的支座传给锚块，并将预应力转移到弧门推力作用线附近，使预应力总吨位与弧门推力之比接近1.0。在锚索设计方面，郭宏磊等［7］通过有限元及弹性理论为基础并结合模型试验，对锚固区的开裂部位及应力分布规律进行研究，提出了一种新型锚块形式；杨晓红等［8］对预应力闸墩主锚索的布置方式进行了研究；张发明等［9］提出了有关预应力锚索设计参数的优化方法；李守巨对闸墩裂缝的形成机理及加固措施等进行研究，并提出了合理的预应力锚索加载方案和锚索布置形式；二滩水电站采用了新型的闸墩预应力锚固技术-U 形锚固式［10］；马吉明等［11］等提出了一种新型的无黏结弯曲预应力锚索结构。

综上所述，目前对预应力闸墩的研究主要是从改变闸墩的结构设计或预应力锚索的形式、空间布置、加载分级等角度出发，几乎没有考虑过锚索张拉顺序对预应力闸墩结构的影响，在施工中也常常被忽略。但随着预应力闸墩布置锚索数量越来越多，布置形式越来越复杂，锚索的张拉次序将成为影响闸墩结构安全的重要因素。

为了弄清不同锚索张拉次序对闸墩结构的影响，本文提出了一种能够有效改善闸墩结构受力状态的预应力锚索张拉方式——交错式对称张拉法。以四川某水库2 号溢流坝段为例，建立闸墩计算模型，拟从数值仿真的角度分析主、次锚索不同的张拉次序对闸墩结构的影响，并从主、次锚索作用方式的角度对改变锚索张拉次序对闸墩产生影响的机理进行探讨。

1 预应力闸墩的模拟方法

1.1 预应力混凝土的模拟

对于有限元建立预应力混凝土结构模型一般有两种方法。一种是直接用荷载代替力筋影响作用于结构，即为等效荷载法；另一种用不同的有限元单元分别模拟钢筋和混凝土，可以获得详细的预应力混凝土结构力学行为，即为实体力筋法［12］。

等效荷载法将预应力筋与混凝土形成一个整体，无法反映出预应力混凝土结构真正的变形行为；不考虑预应力筋的布置导致张拉的具体过程无法模拟，力筋处的混凝土受力结果也不能保证其可靠性［12］。

实体力筋法将混凝土和锚索分别采用不同的单元模拟，锚索的预应力可以采用降温法和初应变法进行施加。降温法需要设置相关单元的实常数，并可以模拟预应力的损失状态。初应变法一般不考虑预应力加载过程产生的损失［12］。

本次建模采用实体力筋法建立预应力闸墩模型，并采用降温法来模拟预应力的施加。

1.2 本构模型

1.2.1 预应力锚索的本构模型

将预应力锚索视为线弹性材料，即假定锚索在加载或卸载中，应力-应变呈线性关系（以锚索的弹性模量E为斜率的直线），其表达式为：

式中：σ为应力；ε为应变；E为锚索的弹性模量。

1.2.2 混凝土的本构模型

将混凝土视为理想弹塑性材料，采用Drucker-Prager 材料模型，即采用Drucker-Prager 准则判别混凝土是否进入塑性状态，并采用相关联的流动法则［13］，其表达式如下：

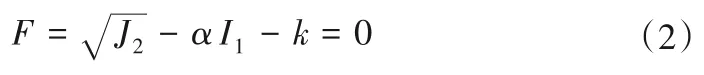
式中：I1和J2分别为应力张量的第一不变量和应力偏张量的第二不变量，其中参数α和k可以用混凝土的黏聚力C和内摩擦角φ来表示：

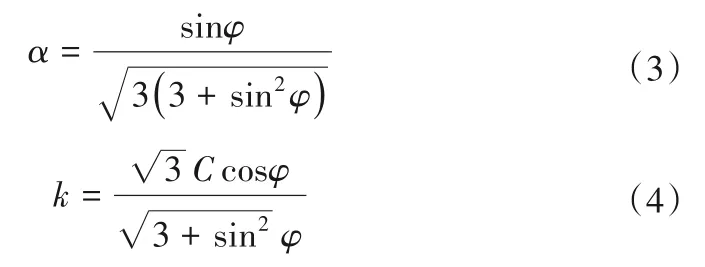
1.3 锚索张拉次序的方法

根据预应力闸墩锚索张拉的基本原则：预应力锚索采用分批、分级对称张拉的方式进行，先张拉次锚索、后张拉主锚索，先张拉监测锚索、后张拉非监测锚索［14］。本文根据这一基本原则，对预应力锚索的张拉次序拟定两种不同的张拉形式，分别为行列式对称张拉、交错式对称张拉。

在对称张拉的基础上，取对称区域的左上角1/4 为例，采用依次张拉的方式对锚索进行张拉［如图1，左上角1/4 区域的张拉顺序为1→2→3→5→7→9（行式张拉法）或为2→5→9→1→3→7（列式张拉法）］，这种方式为行列式对称张拉法。

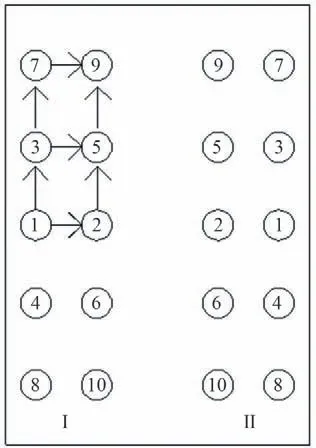
图1 行列式对称张拉法示意图Fig.1 Sketch of determinant symmetric tension method

在对称张拉的基础上，取对称区域的左上角1/4 为例，采用跳序张拉的方式对锚索进行张拉，张拉的次序为交错式（如图2，左上角1/4 区域的张拉顺序为1→2→4→6→7→9），这种方式为交错式对称张拉法。

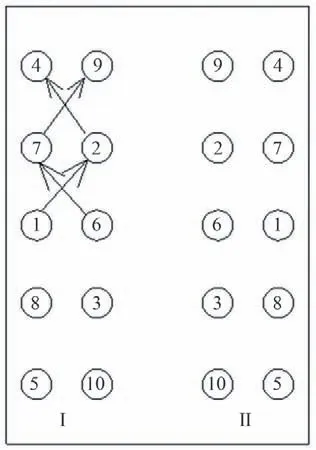
图2 交错式对称张拉法示意图Fig.2 Sketch of staggered symmetrical tension method

2 工程概况

四川某水库工程溢流坝段为混凝土重力坝，由5 孔开敞式实用堰组成，建基面高程为336.00 m，最大坝高39.80 m，堰顶高程为350.00 m，闸墩采用预应力闸墩。孔口净宽14 m，中墩厚为5 m，边墩厚为4.5 m，每个闸孔设有弧形工作闸门。工作门孔口尺寸为14 m×22 m（宽×高），采用弧形闸门液压启闭。该水库溢流坝段从左至右有1～5 个闸孔，对应闸孔底板分缝为4 个坝段，其中：1号溢流坝段为闸孔1+闸孔2的左侧段；2号溢流坝段为闸孔2 右侧段+闸孔3 左侧段；3 号溢流坝段为闸孔3 右侧段+闸孔4左侧段；4号溢流坝段为闸孔4右侧段+闸孔5。

预应力锚索布置分别为：主锚索单边闸墩布置2排，内侧立面为5 层放射状布置，外侧立面为7 层放射状布置，总共12 束。单根锚束预应力4 000 kN（永存锚固力），设计张拉力5 000 kN，超张拉力5 500 kN。水平向布置14 根次锚索，单束永存锚固力2 000 kN，设计张拉力2 350 kN，超张拉力2 585 kN。在正常蓄水位350.00 m 情况下，弧门总推力50 000 kN，分摊到两侧的弧门支座推力F均为25 000 kN。

2号溢流坝段预应力锚索采用后装后张法无黏结预应力施工，分主锚索和次锚索。主锚索顺流向、呈放射状布置，每束主锚索由32 根钢绞线构成；次锚索垂直于流向水平布置，每束次锚索由14根钢绞线构成。主锚索张拉力端设在锚块下游位置，补偿张拉力端设在上游预留孔位置，次锚索锚固于锚块两侧。其中主锚索分为两组，第一组锚索中心距闸墩迎水面60 cm，共7 束，从上到下编号分别为A1～A7（B1～B7），第二组锚索中心距闸墩迎水面120 cm，共5 束，从上到下编号分别为A8～A12（B8～B12）；次锚索共14束，编号为C1～C14。主锚索剖视图如图3，次锚索剖视图如图4。

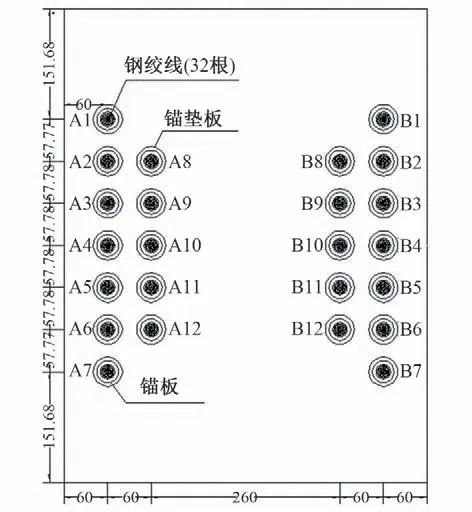
图3 主锚索布置图Fig.3 Layout of main anchor cable

图4 次锚索布置图Fig.4 Layout of sub-major anchor cable

根据上述锚索布置形式，分别采用行列式对称张拉与交错式对称张拉的方式拟定如下4种张拉方案，其中方案一、二采用行列式对称张拉法，方案三、四为交错式对称张拉法。（根据对称性以下方案只列出非对称部分锚索张拉次序）

方案一：

主锚索的张拉次序为：A10→A9→A8→A4→A3→A2→A1

次锚索的张拉次序为：C7→C6→C4→C5→C3→C2→C1

方案二：

主锚索的张拉次序为：A4→A10→A3→A9→A2→A8→A1

次锚索的张拉次序为：C7→C6→C4→C5→C3→C2→C1

方案三：

主锚索的张拉次序为：A4→A10→A3→A8→A1→A9→A2

次锚索的张拉次序为：C7→C3→C5→C6→C4→C1→C2

方案四：

主锚索的张拉次序为：A10→A3→A8→A1→A4→A9→A2

次锚索的张拉次序为：C7→C3→C2→C6→C4→C1→C5

3 不同锚索张拉次序对闸墩结构的影响

本文以四川某水库溢流坝段2 号溢流坝段为例，采用上述两种不同的锚索张拉次序方式，拟定4种锚索张拉次序方案，针对2 号溢流坝段的闸墩两侧闸门关闭工况，对不同的锚索张拉次序对闸墩结构的影响进行分析。

3.1 计算模型

根据该水库2 号溢流坝段设计参数为依据，拟定闸墩两侧闸门关闭的工况施加水荷载、重力荷载以及弧门水推力，建立如图5 所示有限元模型。该模型利用ANSYS 软件建模，其中混凝土采用三维实体单元和理想弹塑性材料并采用Drucker-Prager屈服准则，锚索采用杆单元和线弹性材料，模型结构部分共有节点10 089 个，单元数8 484 个。计算模型具体数值参数如表1所示。

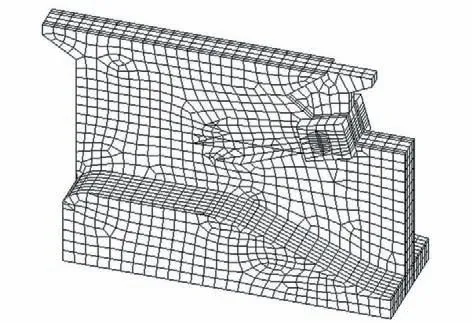
图5 预应力闸墩的数值模型Fig.5 Numerical model of prestressed gate pier

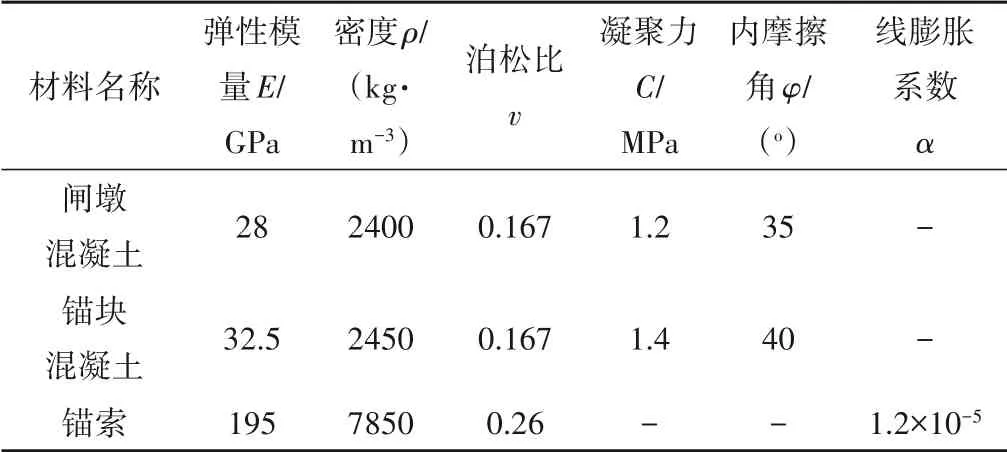
表1 数值计算参数表Tab.1 Parameters for numerical modelling

3.2 不同的锚索张拉次序对锚索应力的影响

图6～图8为不同张拉方案下锚索最大应力的变化。图6为锚索施压后次锚索最大应力值。图7～图8 为锚索施压后主锚索最大应力值。

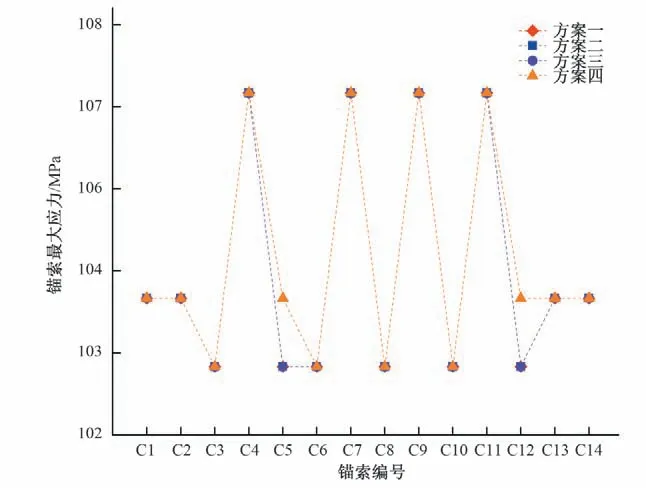
图6 不同方案下次锚索C1～C14的应力变化Fig.6 Stress variation of sub-major anchor cable C1～C14 under different schemes

从图6 中可以看出，各锚索在不同张拉方案下的最大应力值没有明显变化。除了C5 号和C12 号锚索在方案四下的最大应力值比其他方案下的最大应力值大了1%左右，其他次锚索在不同张拉方案下的最大应力值基本一样，说明改变张拉次序对次锚索的应力影响不大。

从图7 中的A1～A12 号锚索可以看出，方案一与方案二的不同编号的锚索之间应力值变化不大，但方案一比方案二的同一编号锚索的应力大，而方案三与方案四的不同编号的锚索之间应力值变化较大，方案三与方案四相同编号锚索的应力相差不大。而图中A8～A12 号锚索，方案一与方案二的不同编号的锚索之间应力值变化较大，且方案一比方案二相同编号锚索的应力值更小，而方案三与方案四的不同编号的锚索之间应力波动不大，方案三与方案四相同编号锚索的应力相差不大。

从图7～图8 中可以看出，采用行列式对称张拉法（方案一、方案二）与采用交错式对称张拉法（方案三、方案四）在同一编号主锚索的应力值上有明显变化，同时不同主锚索之间的应力分布规律也有变化，说明改变张拉次序对主锚索的应力有较大的影响。

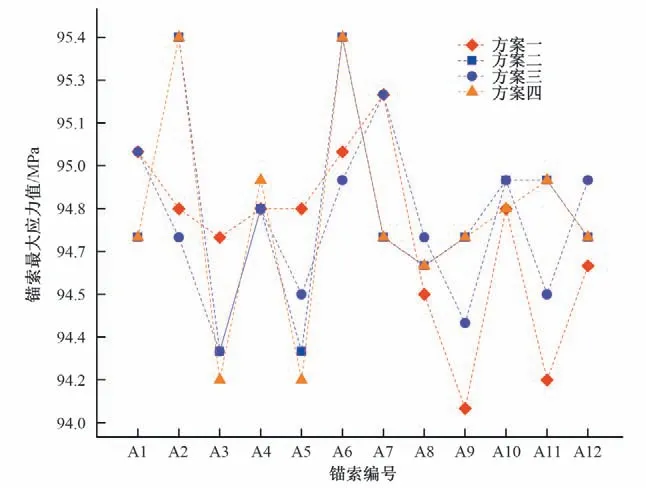
图7 不同方案下主锚索A1～A12的应力变化Fig.7 Stress variation of main anchor cable A1～A12 under different schemes

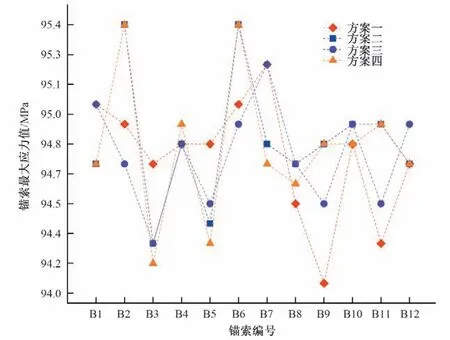
图8 不同方案下主锚索B1～B12的应力变化Fig.8 Stress variation of main anchor cable B1～B12 under different schemes

对比图7 与图8，闸墩两侧相对应编号的锚索应力值基本相同，且在同一侧的锚索中上下对称的锚索应力值相差并不大。不同方案下，锚索应力值的区别主要是非对称区域锚索不同张拉次序引起的。

3.3 不同的锚索张拉次序对闸墩应力的影响

图9为预应力锚索张拉施压后方案一与方案三闸墩内部的应力等值线图，等值线的序号后为其所代表的应力数值。从图9 中不同方案下闸墩的应力等值线图可以看出，尽管采用了相同的有限元计算模型并施加了相同的荷载，仅在改变锚索的张拉次序的情况下，锚索对混凝土的预压效果却产生了差别。以闸墩锚块为例，方案一的最大拉应力值为2.16 MPa；方案三的最大拉应力值为1.05 MPa。从整体的范围来看，采用交错式对称张拉的方式张拉后，预压区内混凝土的拉应力大部分减小到0.5 MPa 以内，而采用行列式对称张拉的方式张拉后，仍有很大范围的混凝土拉应力超过1 MPa。同时，方案一的预压效果主要集中在锚固两端，对中间部位的混凝土预压效果较差。而方案三的应力分布更加分散，预压效果得到了一定的改善。

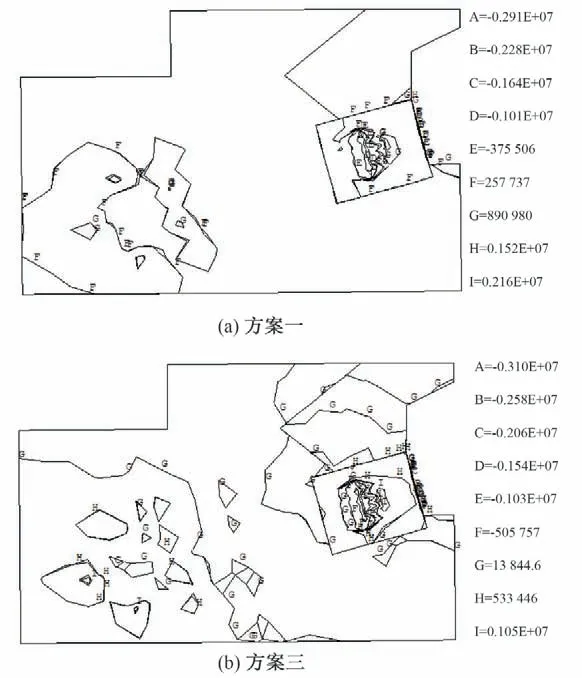
图9 方案一与方案三预压后闸墩内的σ1等值线图（单位：Pa）Fig.9 Contours of σ1 in the gate pier prestressed by scheme 1 and scheme 3

图10～图11 为预应力锚索张拉施压后，方案二与方案四的主、次锚索锚定面上应力等值线。图10为次锚索锚定面的应力等值线图，从图10 中可以看到，方案二和方案四的应力值与应力分布并没有明显的差别，最大拉应力值均在1.05 MPa 左右。图11 为主锚索锚定面的应力等值线图，从图11 中可以看到，方案二的最大应力值和方案四的最大应力值差别明显变大，方案二的最大拉应力值达到了1.66 MPa，同时有一定范围的混凝土拉应力超过了1 MPa。方案四的拉应力值明显更小，最大值为0.78 MPa 左右。同时可以看出，在锚定面上应力主要集中在锚索范围的边缘区域，对于采用两种不同的张拉次序在次锚索锚定面上应力没有明显差别，且应力分布规律基本相同，而主锚索锚定面上应力出现了明显变化，方案二的最大应力值比方案四的最大应力值大一倍左右，且方案二的拉应力区（等值线G所对应的区域）主要在布置锚索区域边缘，方案四的拉应力区（等值线H所对应的区域）主要在布置锚索区域的两侧。

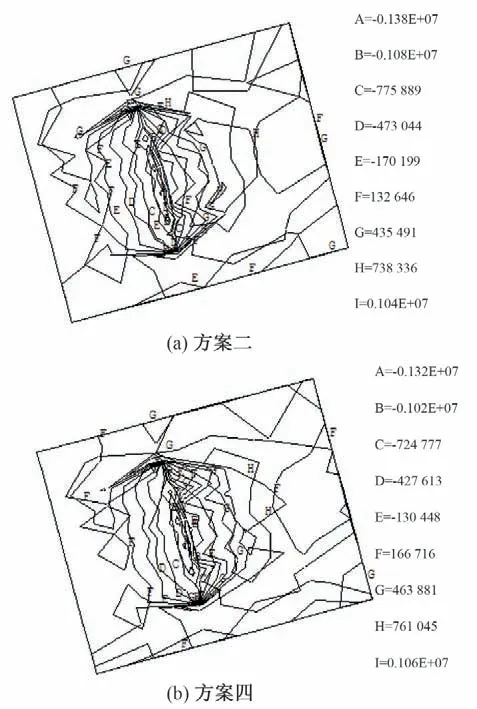
图10 方案二与方案四预压后次锚索锚定面上σ1等值线图（单位：Pa）Fig.10 Contours of σ1 on the anchoring surface of sub-major anchor cable by scheme 2 and scheme 4

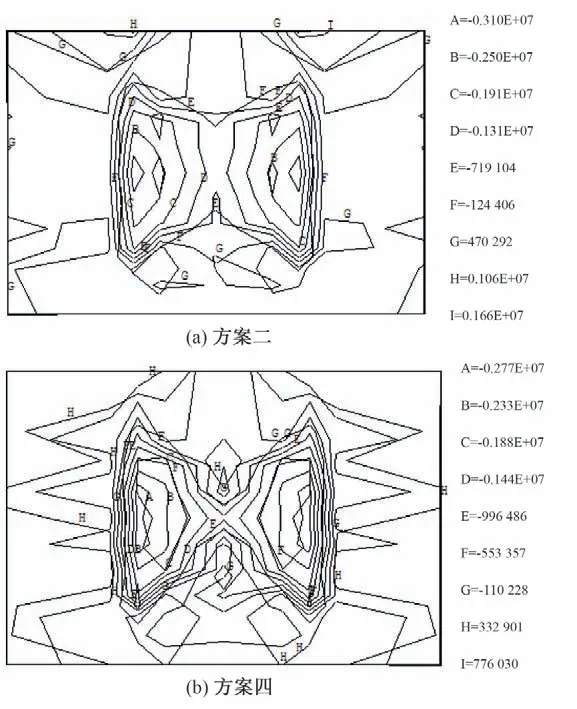
图11 方案二与方案四预压后主锚索锚定面上σ1等值线图（单位：Pa）Fig.11 Contours of σ1 on the anchoring surface of major anchor cable by scheme 2 and scheme 4

图12为不同方案典型部位的应力值变化图，根据锚索张拉后闸墩应力分布情况选取典型部位，比较不同方案下的应力值变化。选取应力分布比较集中的部位分别为，闸墩主锚索上游锚固端（节点号：58208）；闸墩锚块主锚索锚定面上部（节点号：53562）；闸墩锚块主锚索锚定面下部（节点号：58147）；闸墩锚块次锚索锚固端上部（节点号：235650）；闸墩锚块次锚索锚固端下部（节点号：235715）。从图12中不同方案下节点的应力值变化可以看出，次锚索锚固端上下部位应力值完全一样，不同方案之间的应力变化不大，变化值都在0.2 MPa 以内；而主锚索上游锚固端的应力值与次锚索锚固端的应力呈现一种对称分布。在主锚索锚定面下部区域不同方案的应力值并没有明显变化。但是在主锚索锚固端的上部可以看出应力值发生了显著改变，从方案二到方案三应力值有一个明显的下降，说明相比行列式对称张拉法来说，交错式对称张拉法能够明显改善闸墩锚块上部的应力状态。

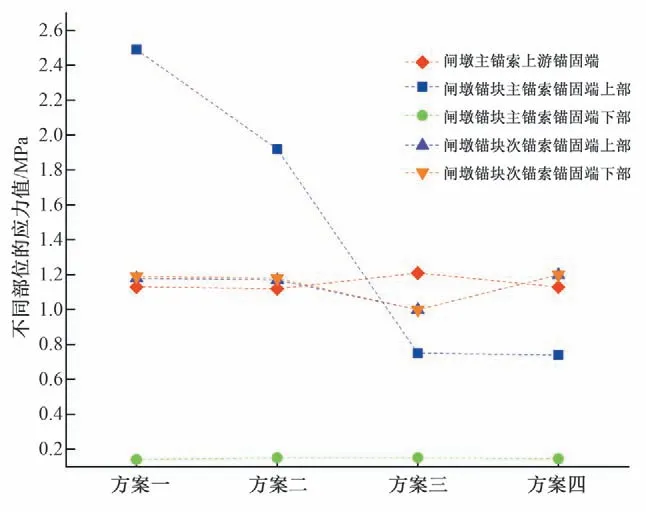
图12 不同方案下典型部位应力变化Fig.12 Stress changes of typical parts under different schemes

3.4 不同的锚索张拉次序对闸墩变形的影响

图13～图15 为不同方案典型部位的位移值随荷载步的变化图。根据闸墩位移变化的变化情况选取典型部位，选取主锚索锚固端的中心部位作X向位移分析；选取锚块主锚索锚定面的下部作Y向位移分析；选取次锚索锚固端的中心部位作Z向位移分析。从图13～图15 中可以看到，采用不同张拉次序方案在张拉的过程中闸墩的位移会发生改变，但是在张拉完成时所有方案的位移值都相同。说明改变锚索张拉次序只会影响张拉过程中闸墩的变形，对闸墩的最终变形影响较小。

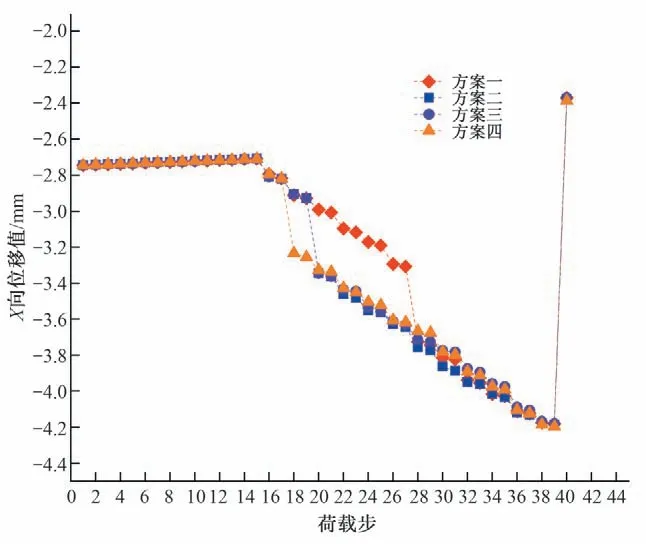
图13 不同方案闸墩X向的位移变化Fig.13 X-direction displacement change of pier in different schemes

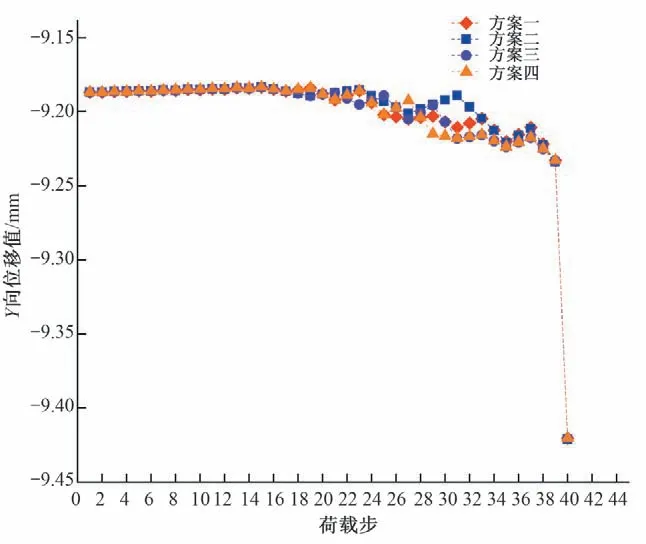
图14 不同方案闸墩Y向的位移变化Fig.14 Y-direction displacement change of pier in different schemes

图15 不同方案闸墩Z向的位移变化Fig.15 Z-direction displacement change of pier in different schemes

3.5 不同的锚索张拉次序对闸墩的应力与变形影响机制的探讨

通过上述有限元计算结果可以看出，预应力锚索采用交错式对称张拉方式可以使闸墩混凝土的拉应力分布更均匀，从而降低拉应力的最大值，改善闸墩的受力状态。结合锚索的应力分布和混凝土的应力与变形变化，对闸墩的影响有以下认识：

（1）改变锚索的张拉次序可能会改变锚索的应力大小，对主锚索而言效果更为明显，次锚索改变并不明显。考虑到主、次锚索的布置和作用，推测这种改变效果的差异可能是与锚索的作用点和施加的荷载大小有关。闸墩上主锚索是沿弧门推力方向平行布置，作用点接近弧门推力作用线方向，主要承担弧门推力。次锚索一般垂直于主锚索布置方向，主要抵消荷载产生的次生拉应力对锚块的不利影响［15］。在预应力闸墩结构中，主锚索承担主要的外荷载，张拉力会较大，而次锚索承担的荷载更小，张拉力也会更小。因此，改变张拉次序对次锚索的影响相对更小。

（2）锚索张拉次序的改变会改变锚索与混凝土的受力状态。预应力结构是在结构受到荷载作用之前，对混凝土预压来发挥混凝土抗压强度高的优势，使混凝土处于弹性工作状态。相比行列式对称张拉的方式，交错式对称张拉会使锚索来承担更多的拉应力，从而降低混凝土的拉应力。这样的应力分布更能充分发挥两种材料的特性，锚索可以承受很大的拉应力，而混凝土则要避免受拉。同时，在交错式对称张拉后的闸墩，只有小部分的拉应力偏大，且均在1 MPa 左右作用在混凝土集中受压区的边缘，范围很小。这种应力分布符合结构要求，且对闸墩受力状态得到极大的改善。

（3）锚索张拉次序的改变对闸墩最终变形的影响较小。这可能是在锚索预应力、水压力及结构自重的共同作用，结构绝大部分处于弹性状态，在总荷载不变的情况下，锚索张拉次序的改变，只是改变了荷载施加的顺序，而对闸墩最终变形的影响较小。

4 结 论

本文以四川某水库闸墩为例建立预应力闸墩的有限元计算模型，利用两种不同类型的张拉方式得到了预应力锚索应力、闸墩混凝土应力与预应力锚索张拉次序之间的关系，对比研究后发现交错式对称张拉的这种方式能够明显改善结构的受力状态。同时，通过对主、次锚索的作用方式和锚索应力、混凝土应力与变形对比，探讨了改变锚索次序对闸墩受力影响的作用机理，得到结论如下。

（1）通过改变锚索张拉次序的方法可以有效改善闸墩的受力状态。改变预应力闸墩锚索的张拉次序会改变预应力锚索与闸墩混凝土之间的应力分配，从而改善闸墩的受力状态。

（2）计算结果表明，采用交错式对称张拉法张拉预应力锚索会使锚索承担的拉应力变大，混凝土承担的拉应力变小，减轻应力集中的影响。

（3）改变锚索的张拉次序对闸墩的最终变形影响较小。在张拉过程中改变锚索张拉的次序，会导致张拉过程中闸墩变形的改变。但在所有锚索张拉完成后，闸墩的荷载保持一致，最后的变形相差不大。

（4）当闸墩采取无黏结直锚索布置时，采取交错式对称张拉的方式会使预应力闸墩的受力更加合理，对拉应力区的预压效果更好。但对改变预应力锚索张拉次序对闸墩结构影响的机理还需要进一步深入研究，同时，随着弯曲锚索的应用，U 形锚索的使用频率增加，交错式对称张拉法同样对U 形锚索的施工与设计提供了新的思路。