月牙肋岔管有限元结构计算基本原则与方法

申 艳，黄永松，冯浩文

（华北电力大学可再生能源学院，北京102206）

1 问题的提出

由于具有受力明确合理、设计方便、水流流态好、水头损失小、结构可靠、制作安装容易等特点，在国内外大中型常规和抽水蓄能电站地下埋管中，月牙肋岔管被广泛应用。但由于埋藏式月牙肋岔管体形及作用机理复杂，用传统的解析方法难以得到理想的计算结果。有限单元法是随着电子计算机的发展而迅速发展起来的一种现代计算方法，它能够模拟复杂的体形和边界条件，且计算精度可靠，是一种有效的结构数值分析手段。有限单元法在方案优化、敏感性分析、计算精度以及研究成本等方面较其他的分析方法有明显的优势。因此，钢岔管设计宜采用三维有限元法进行结构分析。

岔管有限元结构分析的专业性较强，对分析人员的力学基础、研究对象的作用机理和程序熟练程度有较高的要求。在分析过程中，单元类型的选择、网格密度的选取、模型范围的选取、闷头及支撑的模拟方式、边界约束条件等因素对计算结果和分析结论都有一定的影响。因此，有必要对上述各种因素进行系统地分析与评估，提出一套适合埋藏式月牙肋岔管有限元结构计算的基本规定。

2 月牙肋钢岔管有限元结构计算的基本规定

2.1 单元类型的选择

在进行单元类型对有限元计算成果影响分析时，根据月牙岔管的受力特点，对管壳和肋板采用不同单元型式进行研究。月牙肋岔管是一个复杂的空间三维结构，通常可以采用壳单元或实体单元进行模拟。其中壳单元可简化模拟厚度方向尺度远小于整体结构尺寸的模型，一般认为某一方向尺度（厚度方向）小于整体结构尺寸的1/10，且沿厚度方向的应力可忽略的特征的结构。月牙肋岔管的肋板是岔管的加强构件，通常可以采用壳单元或实体单元进行模拟。由于肋板厚度较厚，且在进行肋板应力分析时，肋板厚度方向的应力也需要被关注，故通常在进行有限元结构分析时采用精度较高的八节点实体单元来模拟肋板。

2.1.1 管壳单元

为研究管壳单元类型对计算结果的影响，以圆管段为例分别采用壳单元和实体单元模拟进行有限元结构计算，埋管状态采用点点接触模拟围岩的作用，将结果与解析解进行对比分析。分析表明：当采用4 节点壳单元或8 节点实体单元模拟管壳，采用点点接触单元模拟围岩的作用，单元网格尺寸与主管半径的比值为0.1 时，两种类型的单元均能较好地反应钢管在明管状态和埋管状态下的应力状态，计算成果基本相同，且与理论计算结果也基本一致，管壳采用壳单元和实体单元的计算精度均能满足工程要求。

2.1.2 肋板单元

为研究肋板单元类型对计算结果的影响，以丰宁抽水蓄能电站钢岔管为例，保持钢岔管体形及管壳有限元网格不变，肋板按实体单元和壳单元分别建立有限元模型并进行结构计算。分析表明：

肋板的单元类型对管壳和肋板的应力都有一定的影响。无论明管状态还是埋管状态，单元类型对靠近肋板的管壳影响较大。壳单元与实体单元相比，局部膜应力相对差别均在8%以内，而局部膜应力+弯曲应力则差别较大，差值一般在±（10%～50%）范围，明管状态最大差别可达79%，埋管状态下最大也达69%。对远离肋板的管壳的影响较小，无论是局部膜应力还是弯曲应力，壳单元与实体单元相比差别均较小，相对差别一般不足3%。造成以上结果的原因，主要是两种单元在模拟肋板平面内的刚度时有较大差别所致。

肋板的单元类型对肋板的应力影响程度与管壳相比要大些。明管状态下在两种类型单元的计算结果最大差别为5.4%，出现在部位为肋板腰部断面内侧；埋管状态下，两种类型单元的计算结果最大差别为6.8%，出现部位为肋板腰部断面外侧。

由于肋板沿板厚方向承受拉应力，因此肋板Z向应力也是值得关注的。然而，采用壳单元无法模拟肋板厚度方向受力特点，难以较全面反应肋板的应力状态，而实体单元能较好的模拟肋板的应力状态，因此建议肋板采用实体单元模拟。

2.1.3 网格密度

有限元分析结果的精度与离散模型的网格密度密切相关。模型网格过稀，会对计算精度甚至计算结果产生不利影响，模型网格过密，又会导致有限元模型的规模过大，影响有限元分析的效率。如何在保证计算精度的前提下，划分合理密度的有限元网格，提高计算效率，是需要关注的问题。为说明不同网格密度对月牙肋钢岔管有限元结构计算精度的影响，分别选择对称“Y”形钢岔管和非对称“Y”形钢岔管进行分析，对称“Y”形钢岔管以丰宁钢岔管为例，非对称“Y”形钢岔管以引子渡2 号钢岔管为例。为研究网格密度对计算结果的影响，对同样的钢岔管模型，单元尺寸（C）与公切球半径（R）的比值分别取0.26、0.2、0.13、0.1、0.07 进行计算分析，关键点的位置示意见图1，关键点Mises 应力相对误差与网格密度的关系曲线见图2～图9。通过圆管段的有限元计算结果与解析解计算结果进行对比可知：采用壳单元简化模拟管壳，采用点点接触单元模拟围岩的作用，当C/R=0.1 时，能够较好地反应钢管明管状态和埋管状态下的受力情况，有限元的计算结果与解析解十分接近，明管的计算误差不超过0.3%，埋管的计算误差不超过1.3%。由于岔管应力计算没有解析解，本文假定认为网格密度最大的C/R=0.07 方案的计算结果最接近于理论解，应力相对误差是其他方案的应力值相对于网格密度最大的C/R=0.07 方案的应力值而言的。

图1 关键点位置示意图Fig.1 Schematic diagram of the locations of key points

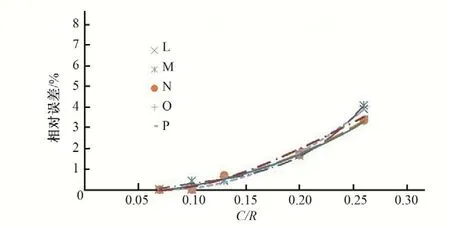
图2 关键点中面Mises应力相对误差与网格密度的关系曲线（对称钢岔管明管状态）Fig.2 Relationship between mean surface Mises stress relative error and grid density at Key points（Open pipe state of symmetric Bifurcation pipe）

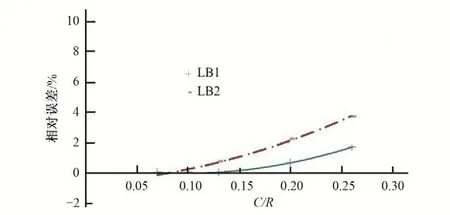
图3 肋板关键点Mises应力相对误差与网格密度的关系曲线（对称钢岔管明管状态）Fig.3 Relationship between Mises stress relative Error of Key floor points and Grid Density（With symmetric Bifurcation pipe open pipe state）

图4 关键点中面Mises应力相对误差与网格密度的关系曲线（对称钢岔管埋管状态）Fig.4 Relationship between mean surface Mises stress relative error and grid density at Key points（Buried state of symmetric Bifurcated steel tubes）

图5 肋板关键点Mises应力相对误差与网格密度的关系曲线（对称钢岔管埋管状态）Fig.5 Relationship between Mises stress relative Error of Key floor points and Grid Density（Buried state of symmetric Bifurcated steel tubes）

图6 关键点中面Mises应力相对误差与网格密度的关系曲线（卜形钢岔管明管状态）Fig.6 Relationship between mean surface Mises stress relative error and grid density at Key points（Asymmetric Y bifurcation pipe state）

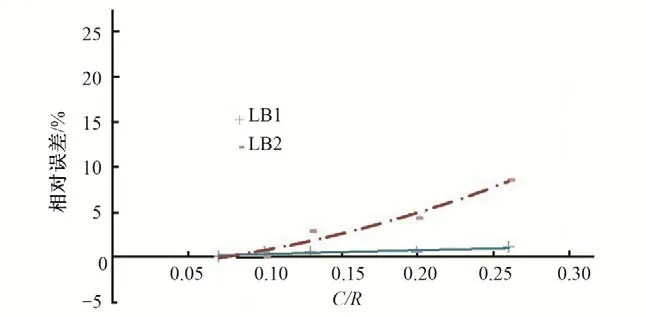
图7 肋板关键点Mises应力相对误差与网格密度的关系曲线（卜形钢岔管明管状态）Fig.7 Relationship between the Mises stress relative error of key floor points and grid density（Asymmetrical Y bifurcation pipe open pipe state）

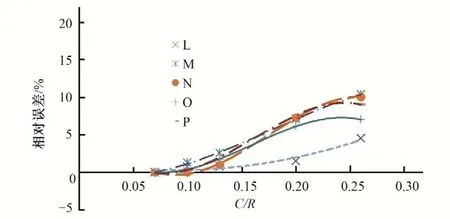
图8 关键点中面Mises应力相对误差与网格密度的关系曲线（卜形钢岔管埋管状态）Fig.8 Relationship between mean surface Mises stress relative error and grid density at Key points（Asymmetric Y bifurcation pipe state）

图9 肋板关键点Mises应力相对误差与网格密度的关系曲线（卜形钢岔管埋管状态）Fig.9 Relationship between the Mises stress relative error of key floor points and grid density（Asymmetrical Y bifurcation pipe open pipe state）

计算成果表明：对于钢岔管有限元计算而言，单元尺寸越小，结果会越精确，计算的相对误差越小。随着单元尺寸的缩小，应力值的相对误差下降很快，但当单元尺寸C/R小于0.1后，随着单元尺寸缩小，应力值的误差降低变得缓慢。无论是明管状态还是埋管状态，当C/R小于0.1时，计算误差相对较小，一般不超过2%，在有限元结构计算时，建议网格密度参数C/R的比值在0.08～0.10之间选取，既能保证计算精度，又不至于模型的规模太大而影响计算分析效率。

2.2 模型范围

为研究模型范围对计算结果的影响，分别以丰宁抽水蓄能电站对称“Y”形钢岔管，和引子渡2号钢岔管非对称Y形钢岔管为例进行说明。对同样的钢岔管模型，支管的长度（L）与主、支管半径（R）的比值分别取1.0、2.0、3.0、4.0、6.0 进行计算分析，关键点的位置示意见图1，关键点Mises应力与模型范围的关系曲线见图10～图17。计算结果表明：模型范围参数L/R从1～6之间变化时，明管状态下，对称钢岔管肋板及腰线折角M、L 点的应力对模型范围较为敏感；非对称Y形钢岔管支管转折点J、M、N、O 的应力对模型范围较为敏感。埋管状态下，受围岩的约束，特征点的Mises 应力变化较小，表明埋管状态下的计算结果对模型范围不敏感。

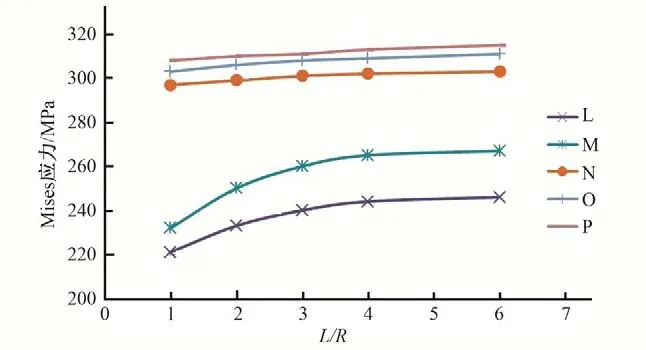
图10 关键点中面Mises应力与模型范围的关系曲线（丰宁钢岔管明管状态）Fig.10 Relationship between Mises stress on the midface of key points and model range（Open pipe condition of Fengning steel bifurcation pipe）

图11 肋板关键点Mises应力与模型范围的关系曲线（丰宁钢岔管明管状态）Fig.11 Relationship between Mises stress on key floor points and model range（Open pipe condition of Fengning steel bifurcation pipe）

图12 关键点中面Mises应力与模型范围的关系曲线（丰宁钢岔管埋管状态）Fig.12 Relationship between Mises stress on the midface of key points and model range（Buried state of Fengning steel bifurcation pipe）

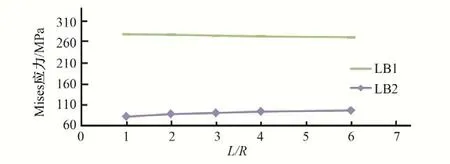
图13 肋板关键点Mises应力与模型范围的关系曲线（丰宁钢岔管埋管状态）Fig.13 Relationship between Mises stress on key floor points and model range（Buried state of Fengning steel bifurcation pipe）

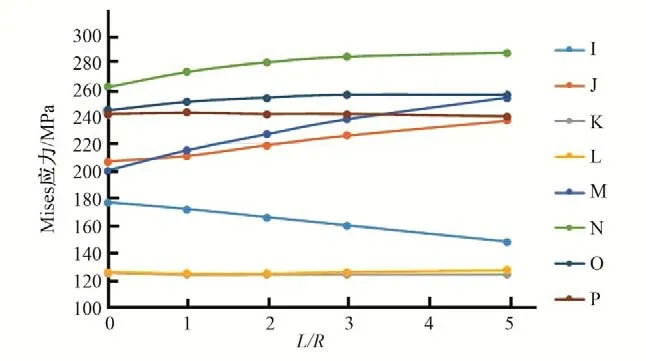
图14 关键点中面Mises应力与模型范围的关系曲线（引子渡2号钢岔管明管状态）Fig.14 Relationship between Mises stress on the midface of key points and model range（Open pipe condition of Yinzidu No.2 steel bifurcation pipe）

图15 肋板关键点Mises应力与模型范围的关系曲线（引子渡2号钢岔管明管状态）Fig.15 Relationship between Mises stress on key floor points and model range（Open pipe condition of Yinzidu No.2 steel bifurcation pipe）

图16 关键点中面Mises应力与模型范围的关系曲线（引子渡2号钢岔管埋管状态）Fig.16 Relationship between Mises stress on the midface of key points and model range（Buried state of Yinzidu No.2 steel bifurcation pipe）

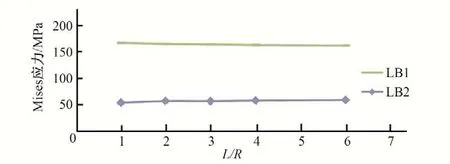
图17 肋板关键点Mises应力与模型范围的关系曲线（引子渡2号钢岔管埋管状态）Fig.17 Relationship between Mises stress on key floor points and model range（（Buried state of Yinzidu No.2 steel bifurcation pipe）

计算范围对计算成果影响主要体现在两方面，一是计算边界约束对钢岔管主体的影响，二是由于钢岔管体形复杂，在内水压力作用下，沿钢岔管轴线会产生不平衡力，如果模型范围选取过大，会导致计算结果误差增大。因此，在明管状态下，钢岔管计算范围受上述两个因素影响，不宜过大，通过计算分析，L/R在3～4 范围内选取比较合适。对埋管状态，由于受到围岩的约束，这种不平衡力对计算成果的影响较小，以计算边界约束条件的影响为主，因此，在选择有限元模型范围时，建议主、支管的长度（L）与主、支管半径（R）的比值取3～4为宜。当岔管公切球与支管直径相差较大时，宜对支管长度适当延长。

2.3 水重及结构自重的影响

通过对丰宁岔管水压试验工况下是否考虑水重及结构自重的有限元计算结果对比分析可知：

（1）无论是否考虑水重及结构自重，岔管的应力分布规律基本相同。相比较而言，是否考虑水重及结构自重，对肋板应力分布的影响较为明显。

（2）当试验压力采用7.3 MPa 时，水重和结构自重所占比重较小，是否考虑水重及结构自重，特征点的应力相差通常不超过10%；当试验压力采用3.7 MPa 时，水重和结构自重所占比重适中，是否考虑水重及结构自重，特征点的应力相差通常不超过20%；当试验压力采用1.0 MPa 时，水重和结构自重所占比重较大，是否考虑水重及结构自重，特征点的应力相差甚至超过了30%；水重及结构自重对计算结果的影响程度与水重及结构自重在荷载中所占的比例有关，所占比例小影响就小，所占比例大影响就大。

（3）采用有限元进行岔管水压试验工况下的结构计算时，考虑水重和结构自重比较容易实现，建议在有限元计算中按实际情况考虑水重和结构自重。

2.4 闷头的模拟方式

在进行水压试验工况的结构计算时，需要考虑闷头的作用，通常有两种模拟方式：①按水压试验的实际情况，在有限元网格划分时考虑闷头；②采用简化的边界条件进行模拟，具体来说：在主管管口施加轴向约束，在两支管管口施加轴向节点拉力，其节点力的合力与其闷头上所受压力相等。简化的模拟方式相对于模拟闷头的实际情况的相对误差一般不超过5%，但在支管过渡锥的相对误差较大，M 点的相对误差甚至超过了10%。建议在进行水压试验工况的结构计算时，按闷头的实际情况模拟闷头的作用。

2.5 支撑的模拟方式

通过对丰宁岔管水压试验工况下不考虑支撑和模拟支撑的有限元计算结果对比分析可知：

（1）从上半部分的应力分布规律来看，是否考虑支撑对应力部分影响较小；从下半部分的应力云图以及支墩处节点的应力可以看出，由于考虑支撑的模型同时考虑了结构自重、水重以及支墩的作用，部分支墩处的节点呈现一定的弯曲作用和应力集中，但总体的应力水平不高。

（2）支撑的模拟对各个特征点应力有一定的影响，当具体到每个特征点，其影响程度有所不同，是否考虑支撑的相对误差一般不超过5%，但是在支管过渡锥的特征点的相对误差超过了10%。

（3）由于在内水压力作用下，肋板处于偏心受弯的受力情况，是否考虑支撑、水重、结构自重对于肋板的应力影响较为明显；以丰宁为例，在水压试验工况下，肋板的应力水平不高，是否考虑支撑对肋板特征点计算相对偏差超过20%。

（4）由于是否考虑支撑对个别部位应力的影响较大，建议在进行水压试验工况结构计算时，建议尽量按照实际情况模拟支撑的作用。

2.6 约束条件

通过对丰宁岔管运行工况下，不同约束条件下的有限元计算结果对比分析可知：

（1）无论是在明管状态还是埋管状态，全约束和平动3自由度约束的计算结果几乎一致，可见是否约束岔管端部边界的旋转自由度对计算结果影响可以忽略。

（2）在明管状态下，对比平动3自由度约束以及法向约束的计算结果可知，如果只是约束法向的自由度而不约束平面内的自由度，特征点的计算结果相差一般在5%以内，也有个别特征点如肋板、肋旁管壁，支管转折点等部位相差超过了10%，边界约束条件的影响不可以忽略。

（3）在埋管状态下，对比全约束、平动3自由度、法向约束等3 种不同约束条件下的计算结果可知：由于围岩的约束作用较强，岔管端部的约束条件对岔管的计算结果影响很小，一般不超过1%。

（4）基于以上几点，并考虑到明管状态的分析需要，建议在进行岔管有限元结构计算时，模型端部的约束条件选取全约束或平动3自由度约束。

3 结 论

（1）在月牙肋岔管有限元结构计算中，为保证计算精度单元建议按照以下原则进行选择：肋板选择8节点实体单元模拟；管壳选择4节点壳单元模拟；埋管状态下，钢衬与围岩的联合承载选择点点接触单元进行模拟。

（2）对于岔管有限元计算而言，单元尺寸越小，结果会越精确，计算的相对误差越小。随着单元尺寸的缩小，应力值的相对误差下降很快，但当单元尺寸缩小到一定程度后，应力值的相对误差下降变成缓慢。无论是明管状态还是埋管状态，当单元尺寸与公切球半径的比值建议在0.08～0.10之间选择，计算相对误差相对较小，可以满足工程计算精度的要求，也不至于使网格过密而影响计算分析效率。

（3）在选择有限元模型范围时，为了减小约束端的局部应力影响，主、支管的长度（L）与主、支管半径（R）的比值建议在3～4 范围选择。当公切球与支管直径相差较大时，宜对支管长度适当延长。

（4）水重及结构自重在荷载中所占的比例大小决定水重及结构自重对计算结果的影响程度；采用有限元进行岔管水压试验工况下的结构计算时，考虑水重和结构自重比较容易实现，建议在有限元计算中按实际情况考虑。

（5）通过对实际闷头和简化模拟两种方式的对比分析可知，简化的模拟方式相对于模拟闷头的实际情况的相对误差一般不超过5%，但是在支管过渡锥的相对误差较大，M 点的相对误差甚至超过了10%。因此，在进行水压试验工况的有限元结构计算时，建议按照水压试验的实际情况，在有限元网格划分时考虑闷头。

（6）通过对丰宁岔管水压试验工况下不考虑支撑和模拟支撑的有限元计算结果对比分析可知，是否考虑支撑的相对误差一般不超过5%，但是在支管过渡锥的特征点以及肋板特征点，计算相对误差较大；另外，在支撑部位也会引起局部的弯曲应力和应力集中。因此，在进行水压试验工况的有限元结构计算时，建议按照支撑的实际情况，在有限元结构计算中予以考虑。

（7）约束条件不同对明管状态下的影响要大于埋管状态，考虑到明管状态的分析需要，建议在进行岔管有限元结构计算时，模型端部的约束条件选取全约束或平动3自由度约束。