基于优化时间函数的走向主断面动态预计模型与算法

张 兵，崔希民，袁德宝，贺军亮，郭娅玲

(1.石家庄学院 资源与环境科学学院，河北 石家庄 050035；2.中国矿业大学(北京)地球科学与测绘工程学院，北京 100083)

0 引 言

开采沉陷预计方法中，无论是概率积分法，还是典型曲线法等，计算的都是地表稳定后的沉降和变形值[1-3]，经过多年发展，我国学者在静态预计方面的研究成果较为丰富，且非常成熟。众所周知，地表移动和变形是一个复杂的过程，与多因素有关，如开采速度、覆岩性质、煤层倾角等[4-8]。研究地表随时间变化的动态过程同样具有重要的现实意义，可为采前建筑物保护、采后损害鉴定、采空区土地复垦利用等提供指导。国外动态预计研究可追溯到20世纪20—30年代，我国学者直到20世纪80年代，才开始重视动态预计相关研究，并在近年来取得了较大的进展。崔希民等[6]对最常用的动态预计“Knothe时间函数”进行了研究，指出了其在理论上的不足，给出了理想时间函数的图像形态；常占强等[9]为了改善Knothe时间函数在地表下沉初始阶段预计精度较低的问题，将该函数进行了分段表达，建立了“分段Knothe时间函数模型”。胡青峰等[10]对Knothe时间参数的影响因素进行了分析，给出了时间参数的直接求取方法，提高了编程计算的效率。陈磊等[11]在动态预计中使用幂指数 Knothe 时间函数模型，并利用InSAR与水准测量数据对该时间函数进行求参。郭旭炜等[12]对分段Knothe时间函数的参数进行了研究，指出其参数会随开采过程而变化，并给出了动态求参方法。另外，在动态预计方法方面，杨泽发等[13]利用InSAR观测值与Logistic模型之间的函数关系求取后者时间参数，进而再采用Logistic模型进行动态预计。李怀展等[14]基于加权法和地质力学参数的敏感性，提出了一种地表沉降动态计算模型，并用实例说明了该方法具有较高的精度。

通过文献分析可知，在动态预计方面，学者们提出了各种方法，其中对Knothe时间函数的研究和改进涉及较多，说明了该时间函数仍然具有很强的适用性；另外，现有方法中，很多时间函数参数的求取依赖大量实测数据，且模型较为复杂，在实际应用中存在较大困难。为了操作简便，保证较高的预计精度，选择“分段Knothe时间函数”作为动态预计时间函数—笔者曾对其进行过优化，并给出可靠时间参数计算方法[15-16]—研究走向主断面地表沉陷动态预计方法，建立预计公式并设计相应的程序算法。限于篇幅，倾向主断面和全盆地动态预计方法将另文研究。

1 动态预计基本原理

1.1 动态单元划分

在动态预计实践中，国内外的普遍做法是通过将地下开采单元所引起的沉陷静态预计结果乘以对应的时间函数值来实现。因此，在动态预计中除了选择合理的时间函数外，还需要根据开采情况对工作面进行合理的划分，通常是将工作面划分为距离相等或不相等的多个单元，称其为“动态开采单元”，划分方法主要有“周期来压步距法”和“有效尺寸分割法”[17-18]。

在实践中，为了方便操作，通常采用有效尺寸分割法，如图1所示(X为工作面到开切眼的距离，W为地表下沉量)。

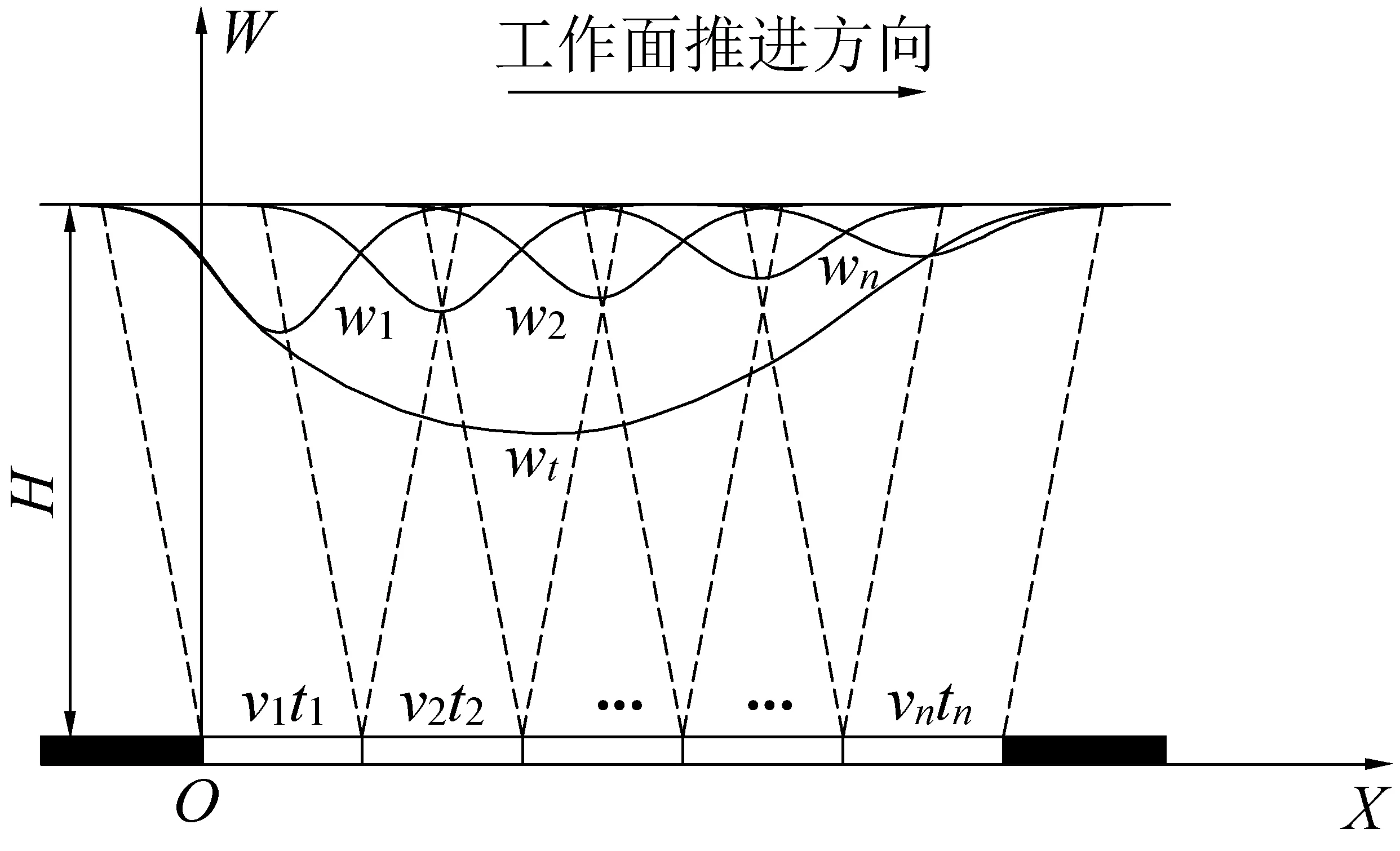
H—采深；wi—某点地表下沉量图1 动态单元开采对地表点下沉的动态影响Fig.1 Dynamic influence when mining dynamic unit on surface subsidence

图1中v1t1表示第1个动态单元的长度，v1表示第1个动态单元的开采速度，t1表示第1个动态单元采完所经历的时间；同理，v2t2表示第2个动态单元的长度，vntn表示第n个动态单元的长度。w1表示第n个单元刚采完时，第1个动态单元开采对地表下沉的影响，w2表示第n个动态单元刚采完时，第2个动态单元对地表下沉的影响；w3～wn的意义以此类比。对比可知，第1个动态单元的影响最大，第n个单元的影响最小，原因是，当第n个动态单元刚采完时，第1个动态单元对地表影响的总时间是t1、t2、…、tn之和，而第2个动态单元对地表影响的总时间则是t2、t3、…、tn之和，比第1个单元的影响时间短，因此其影响也小，同理，由于影响时间不同，其他单元的影响会依次减小。在t1+t2+…+tn时刻，将工作面1～n个单元开采对地表的影响进行叠加求和，即可得到此时刻的地表下沉，图1中Wt即t1+t2+…+tn时刻的动态下沉曲线。因此，要想求某时刻T的地表下沉量，需首先计算各单元在T时刻的动态影响w1、w2、…、wn，这就需要通过采用时间函数，将各动态单元的静态影响与时间系数联系起来，用系数对其影响进行调整。

1.2 动态预计时间函数及其计算

本文选择的时间函数是“优化分段Knothe时间函数”，简称：“优化分段时间函数”，笔者曾改进了原分段函数的不足[15]，并通过实测数据证明了其在动态预计中的可靠性。优化分段时间函数理论模型如式(1)所示：

(1)

式中：τ为地表点出现最大下沉速度时刻；T为地表移动变形总时间；c为与地质、采矿条件有关的时间系数；t为给定的预计时刻。

在动态预计时，首先要计算每个动态单元所对应的时间函数值，函数值可理解为开采影响调整系数。如果在t时刻进行预计，则第1个动态单元的调整系数可用Φt表示；第2个动态单元的调整系数用Φ(t-t1)表示；第n个动态单元的调整系数则用Φ(t-t1-…-tn-1)表示，根据时间函数的意义，第1个动态单元时间函数值可采用式(1)直接求得，第2到第n个动态单元的时间调整系数可用式(2)、式(3)等进行计算。

第2个动态开采单元时间函数值计算公式为

(2)

同理，可求第n个单元时间函数式，即

(3)

2 走向主断面动态预计理论模型

2.1 走向动态单元有限开采原理

对于每个动态单元，其开采影响符合有限开采原理，可采用概率积分模型，采用有限开采相应计算公式，具体如图2所示。

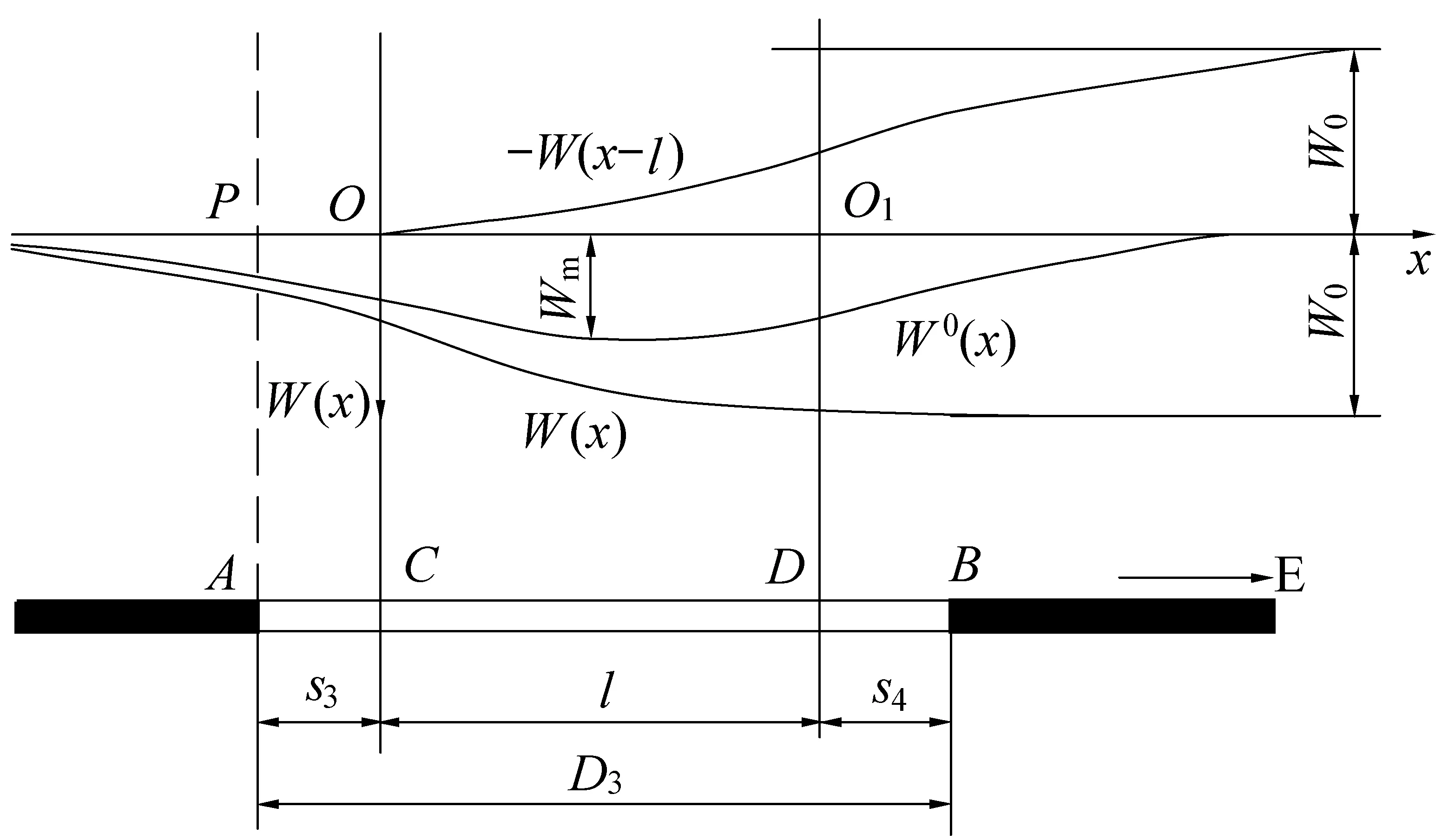
图2 有限开采地表走向主断面预计叠加原理Fig.2 Superposition principle in strike main section prediction when finite mining

图2中，s3、s4为工作面左右拐点偏移距；AB为实采边界，计算时坐标原点位于O处，W(x)表示将x>-s3的所有煤层采出引起的地表下沉曲线；而W(x-l)对应的是AB煤层未采，只采x>(l+S4)的煤层时的地表下沉，那么，如果仅开采AB煤层，其对地表下沉量W0(x)就可用W0(x)=W(x)-W(x-l)求解，其结果可用图中W0(x)表示。如果不考虑拐点偏距的影响，将坐标原点设在P处，则AB煤层开采影响可用W0(x)=W(x)-W(x-D3)来计算。

2.2 走向主断面动态预计模型构建

在建立模型时，将坐标原点设在图2中P点处，纵轴表示地表下沉，x轴表示地表点位置。结合图1，第1个动态单元开采后，该单元的起点横坐标为0，终点横坐标为v1t1，设其下沉影响用W1(x)表示，考虑拐点偏距影响，参照有限开采原理[1]，其终态影响可用式(4)计算，即

W1(x)=W(x-s3)-W[x-s3-(v1t1-s3)]=
W(x-s3)-W(x-v1t1)

(4)

如果其他动态单元均未开采，只开采第2个动态单元，则其起点横坐标x为v1t1，终点横坐标为v2t2，依照式(4)，其对地表下沉的终态影响可用式(5)计算，即

W2(x)=W(x-v1t1)-W(x-v1t1-v2t2)

(5)

同理，可推导第n个动态单元单独开采后Wn(x)的计算式，即

Wn(x)=W(x-v1t1-…-vn-1tn-1)-W[x

-(v1t1+…+vn-1tn-1+vntn-s4)]

(6)

根据概率积分法原理，上述公式中W(x)按照式(7)进行计算。即

(7)

式中，W0为最大下沉量。

式(4)—式(6)计算的是各动态单元独立开采对地表下沉的终态影响，按照动态预计原理，如果将各单元的终态影响乘以对应的时间函数值，即可得指定预计时刻的地表动态下沉预计公式，见式(8)。

W(x,t)=Φ(t)[W(x-s3)-W(x-v1t1)]+
Φ(t-t1)[W(x-v1t1)-W(x-v1t1-1v2t2)]+
Φ(t-t1-t2)[W(x-v1t1-v2t2)-W(x-v1t1-
v2t2-v3t3)]+…+Φ(t-t1-t2-…-tn-1)
{W(x-v1t1-…-vn-1tn-1)-W[x-
(v1t1+…+vn-1tn-1+vntn-s4)]}

(8)

如果每个单元的开采速度和开采时间均相等，即v1=v2=…=vn=vd，t1=t2=…=tn=td，式(8)可进一步化简。同理，地表水平移动、水平变形、倾斜、曲率等，可根据相应概率积分公式参照求得。

3 走向主断面动态预计算法

3.1 算法基本思想

动态预计需考虑的问题比静态预计更为复杂，首先是动态单元的划分问题，其次是，在预计时刻各单元开采状态的确定问题(存在3种情况：动态单元已开采完毕、部分开采完毕、没有开采)。时间函数选定后，动态单元长度的大小对预计精度也有较大影响，计算模型中通常以0.1H0(H0为平均采深)作为动态单元的长度[17]。如果以平均速度代入计算，则每个动态单元的长度除了最后一个，其余全部相等。计算步骤如下：

1)步骤1：在给定的预计时刻T，判断1～n个动态单元的开采状态，即：已经开采、部分开采或均未开采。当T比开采所有煤层所需的总时间TZ大时，则表明所有单元均已采完。

2)步骤2：对于已采单元，计算其在T时刻对应的时间函数值，由于模型采用的是分段时间函数，需判断T与参数τ的大小，如后者大，采用分段函数第一段计算，如前者大，则采用第2段计算。

3)步骤3：采用式(6)计算各单元开采对地表移动变形的静态影响，再将其乘以对应的时间函数值即可得到T时刻各单元开采的下沉预计值。

4)步骤4：将第3步各单元预计值进行叠加求和，可得到预计时刻已采单元对地表下沉的总影响。

5)步骤5：绘制走向主断面移动变形图，为了对比，可改变T值重新计算，将下沉，倾斜等分别绘制在同一幅图中，观察地表移动变形的动态发展规律。

3.2 算法的实现

在将预计模型转换为计算机程序的过程中，需考虑各动态单元时间函数值的计算方法问题，在计算时，如何判断各单元的时间函数值应采用第1或第2段函数进行计算是难点，具体算法见表1。

表1 优化分段时间函数编程算法Table 1 Programming algorithm of optimized segmented Knothe time function

上述算法解决了各动态单元时间函数值的求取问题。除了计算时间函数值，在走向主断面的动态预计模型中，还需计算各单元对地表移动的静态影响，难点在于考虑拐点偏移距后，各单元起始坐标如何确定，相应算法见表2。

表2 走向主断面动态预计算法Table 2 Dynamic prediction algorithm of strike main section

4 走向主断面动态预计实例

4.1 预计实例1

据文献[19]，某矿工作面1002的静态预计参数如下：D3=1 000 m，D1=250 m，m=3 m，q=0.78，H0=500 m，tanβ=2.0，s3=s4=50 m，b=0.28。动态参数v=5.0 m/d，动态单元长度L=0.1H0，时间参数c和τ，按文献[16]中方法求得。用本文模型与算法编制的程序，在不同的预计时刻T，对1002工作面开采时地表走向主断面下沉和倾斜进行动态预计，结果如图3所示。由于在倾向上为非充分开采，需考虑非充分采动因素，故地表实际下沉比充分采动最大下沉量W0(2.38 m)小很多，从图中还可看出地表下沉的动态变化规律。当T=500 d时，地表下沉和倾斜很小，这是由于此时工作面仅开采了210 m，并且采深较大的缘故。

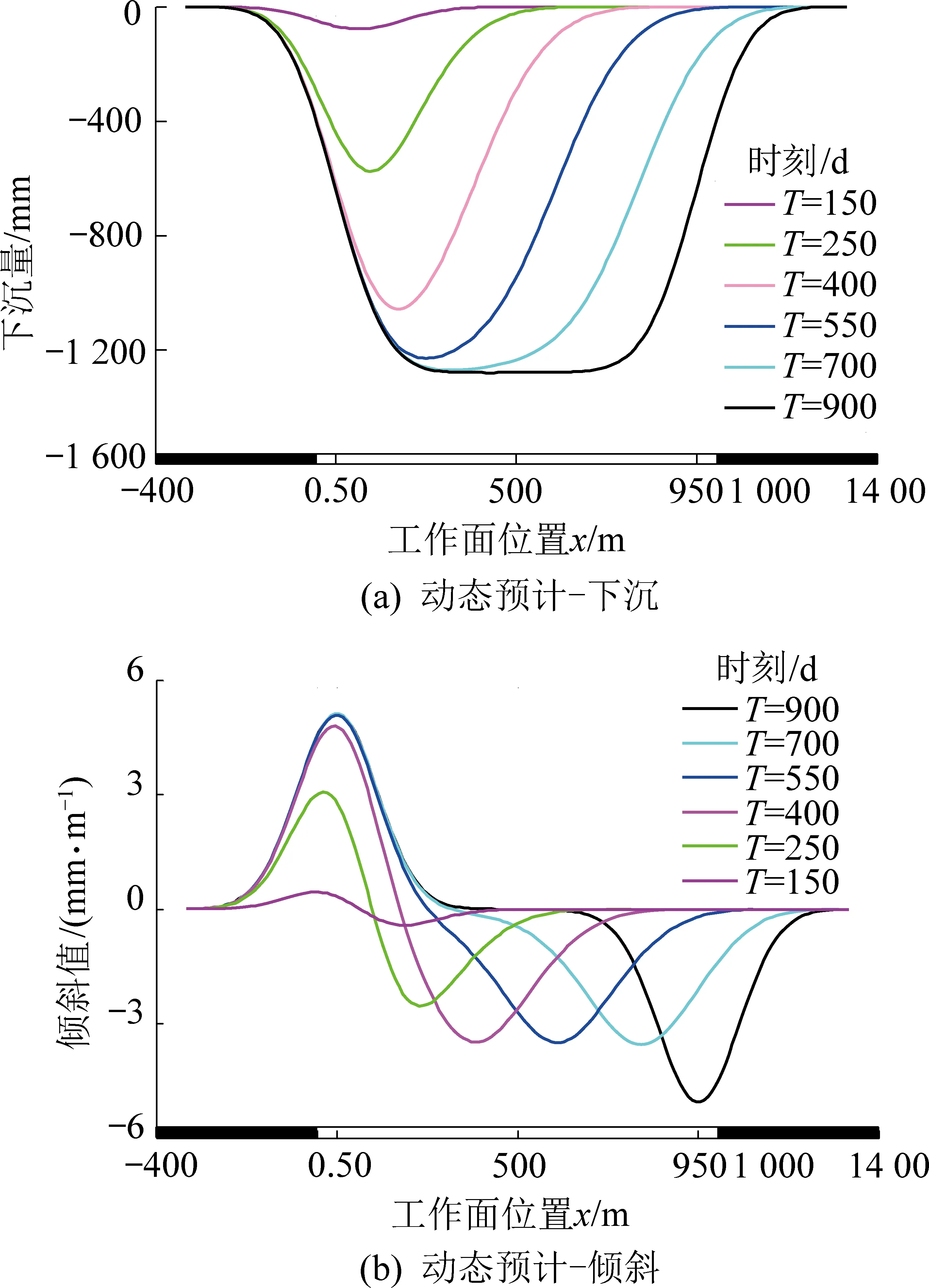
图3 工作面1002走向主断面下沉与倾斜动态预计Fig.3 Dynamic prediction of surface subsidence and inclination in strick principal section of No.1002 working face

随着T增加，地表下沉和倾斜不断增大，影响范围也逐渐扩大。当T=900 d时，距离工作面开采结束又历时700 d，地表移动已趋于稳定，再增加T，地表下沉和倾斜曲线不会再发生任何改变，此时，所有动态单元对应的时间函数值均为1，代表着各单元开采影响达到了最大值。由于计算模型中考虑了拐点偏移距的影响，图3中的下沉曲线拐点出现在实际拐点的正上方，而预计的倾斜值，在拐点处也达到了最大值，这与理论所揭示的规律相吻合。

4.2 预计实例2

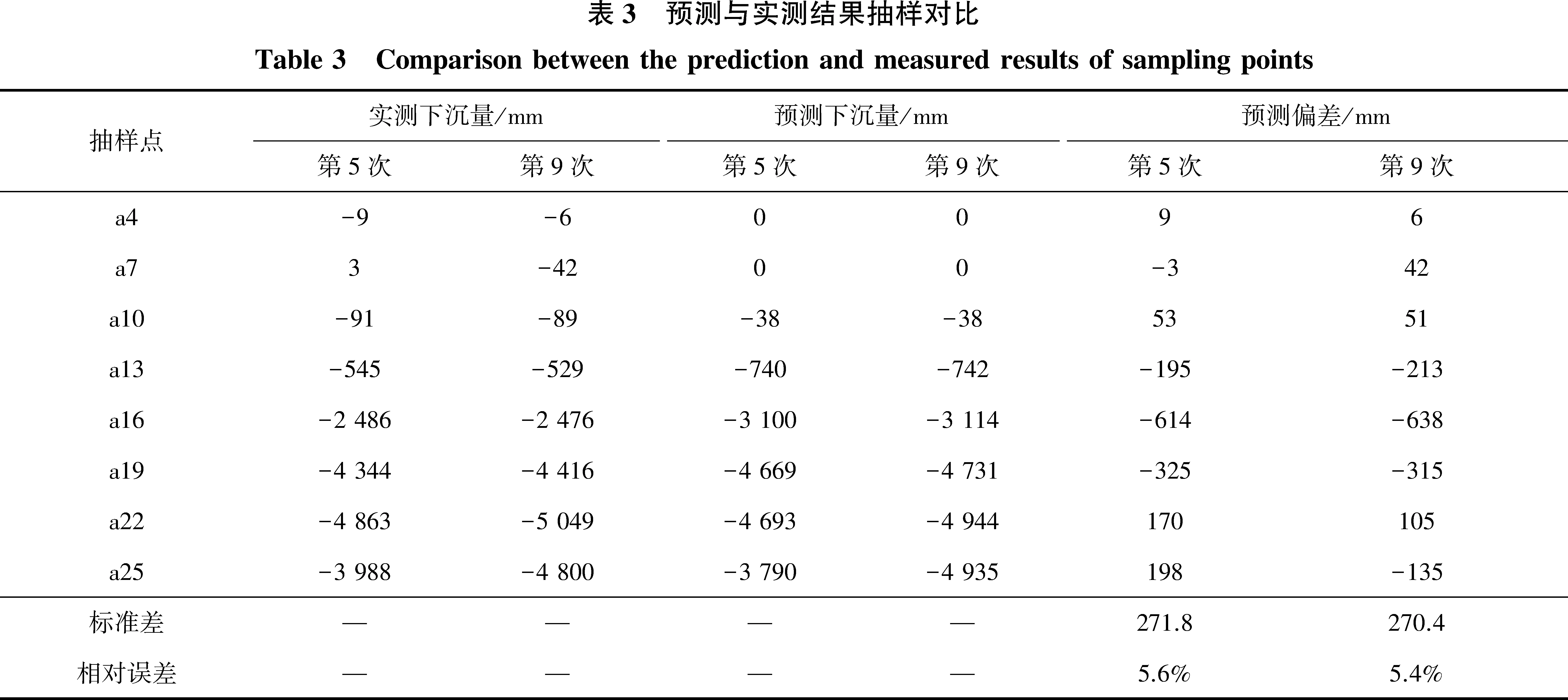
为了验证模型精度的可靠性，另对官地矿29401工作面开采走向主断面进行动态预计，工作面相关概率积分参数见参考文献[10]，动态预计时间参数的计算方法同实例1。预计时间节点与实际观测时间相对应，实测9次即进行了9次预计。由于走向监测点较多，预计后，抽样对其第5次和第9次预计结果与实测结果进行对比分析，并统计精度，见表3。

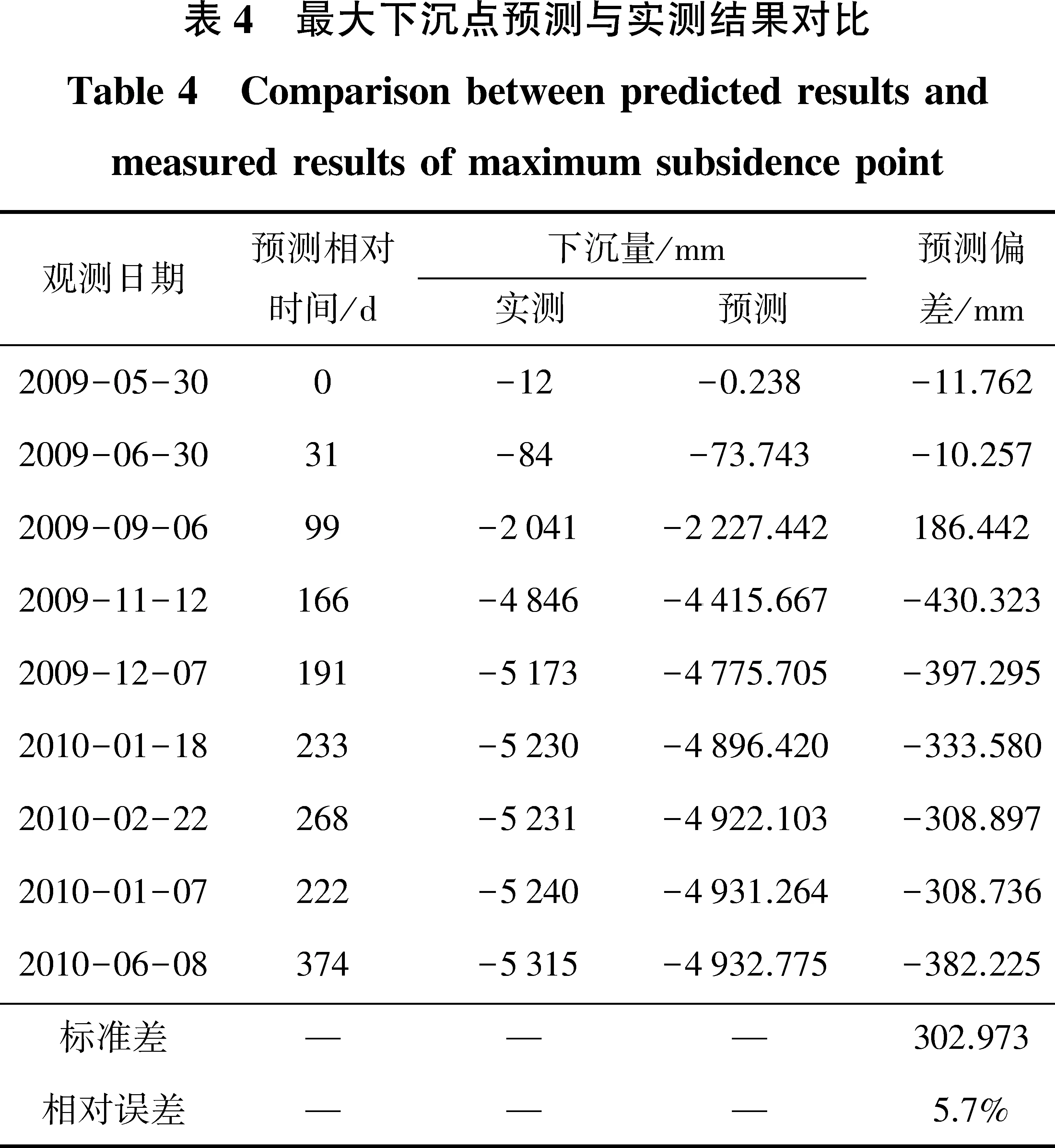
提取最大下沉点的9次预计结果，将其与实测结果进行对比分析，并统计其精度，见表4。

在开采沉陷研究中，预计结果精度常采用标准差m和相对误差f来衡量[10,20]，可分别用式(9)和式(10)进行计算。

(9)

(10)

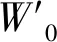
通过表4可知，通过对走向监测点的抽样分析，其第5次预计的标准差为271.8 mm，相对误差为5.6%，第9次预计标准差为270.4 mm，相对误差为5.4%。

通过表3可知，在对最大下沉点的动态预计中，前3期所得到的预测与实测结果较为接近，相差最大约186 mm，预测误差较小，后6期的预测结果小于实测结果，预测误差相对较大。经统计，本次预计的最大下沉点预计中误差约为±303 mm，预计相对误差则在5.7%左右，预计精度较为稳定。

5 结 论

1)优化分段Knothe时间函数完善了原函数的不足，使其具有更好的适应性。以该函数为基础，推导了各动态单元时间函数值的计算公式，结合概率积分法，建立了适应于水平和缓倾斜煤层开采的地表走向主断面沉降变形动态预计模型。

2)根据动态预计原理和预计模型，探讨了动态预计计算的详细流程，设计了时间函数值和走向主断面沉降变形计算的编程算法，并编制了程序。

3)1002工作面预计实践表明：当给定的预计时间足够大，动态预计结果与静态预计结果相吻合，并在拐点偏移距处的倾斜值达到了理论最大值。29401工作面预计结果表明：其走向主断面地表点动态预计精度约在6%以内，证明了本文预计模型和算法具有较高的精度。