角件旋转式模块单元连接节点抗拉性能研究*

2021-08-06王小盾丛子怡刘佳迪

建筑结构 2021年13期

王小盾，丛子怡，刘佳迪

(天津大学建筑工程学院，天津 300072)

0 引言

建筑工业化作为传统建筑业中手工业生产方式的替代品，是一种高度集中、高水平、高效率的现代化科学管理工业生产方式。它拥有标准化的建筑设计、工厂化生产的构件、机械化的施工以及科学化的组织管理。建筑产业化则是对建筑工业化产品的开发，并进行能源、材料、建筑产品的销售，是一种新的技术与市场经济的结合方式。实现建筑工业化的关键产品之一为装配化建筑，建筑构配件由工厂加工后运输现场，装配完毕形成建筑。模块化则是每个具有独立使用功能的单元和构件，可以组成装配化建筑。而模块建筑则是以每个房间作为模块单元，在工厂中进行预制生产，运输至现场后通过可靠的连接方式组装成为建筑整体。因此，模块建筑是建筑工业化发展的终极产物，工业化程度极高，也可以将其视作一种商品[1-2]。

钢结构模块建筑与传统建筑最大的两个区别是节点连接和其连接单元，由于模块建筑由模块单元拼接而成，每层会出现两个楼板，不同于传统建筑的“一柱双梁”，结构会出现角柱的“两柱四梁”，边柱的“四柱八梁”和中柱的“八柱十六梁”的情况。传统的节点便不能满足要求，构造简单、操作方便、受力明确的连接节点尤为关键[3-4]。

目前钢结构模块建筑连接节点形式有预应力连接节点[5]、螺栓封板组合节点[6]、梁梁连接节点[1]、螺栓连接节点[7]、梁柱内套筒组合螺栓连接节点[8]等。角件旋转式模块单元连接节点则是一种新型的钢结构模块单元连接节点，如图1所示，其详细构造如图2所示。这种节点可以解决模块建筑中模块单元角部连接问题，节点受力明确，可以抵抗水平剪力与竖直拉力，构造简单、合理，安装快速、方便，而且可以循环使用、拆卸更换[9-10]，但是目前针对这种类型的节点研究较少。

图1 角件旋转式模块单元连接节点

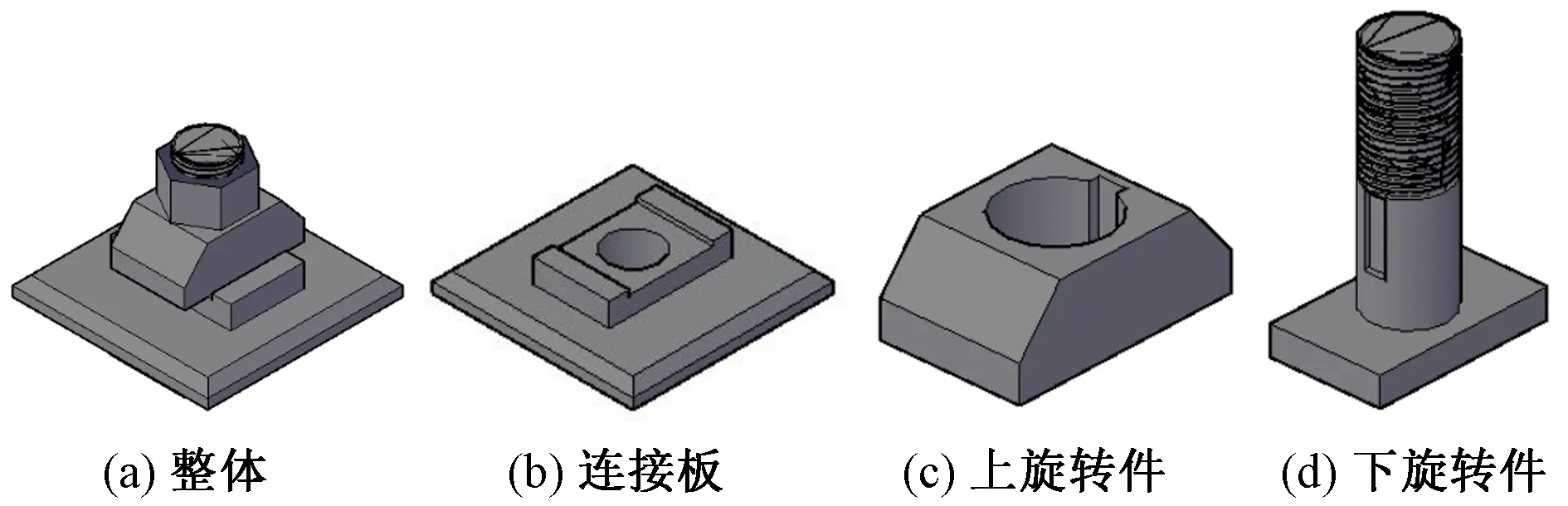
图2 节点旋转件

本文主要针对角件旋转式模块单元连接节点进行试验研究及有限元分析，考察节点在抗拉作用下的应力分布、承载力机制及破坏形式，以及不同参数对于节点抗拉承载力和受力状态的影响，并对节点提出构造建议。

1 试验概况

1.1 试件设计

角件旋转式模块单元连接节点静力抗拉试验采用足尺模型，共有试件2个，编号为T1，T2，上下模块只取连接部位，模块柱取300mm高，采用截面尺寸为200mm×18mm的方钢管，并在该模块柱端部焊接300mm×300mm×30mm方形底板，以及焊接加劲肋进行加强保护，另一端与相同尺寸的带孔耳板垂直焊接连接，两端耳板与拉力机夹具通过销轴固定，一端作为固定端，一端作为加载端，试件具体尺寸如图3所示。

图3 角件旋转式模块单元连接节点抗拉试件尺寸图

1.2 量测内容

角件旋转式模块单元连接节点静力抗拉试验位移量测方案如图4所示，共布置1个位移计，编号为D1，布置于模块柱之上，用以量测节点受拉时，上下角件之间的相对位移。

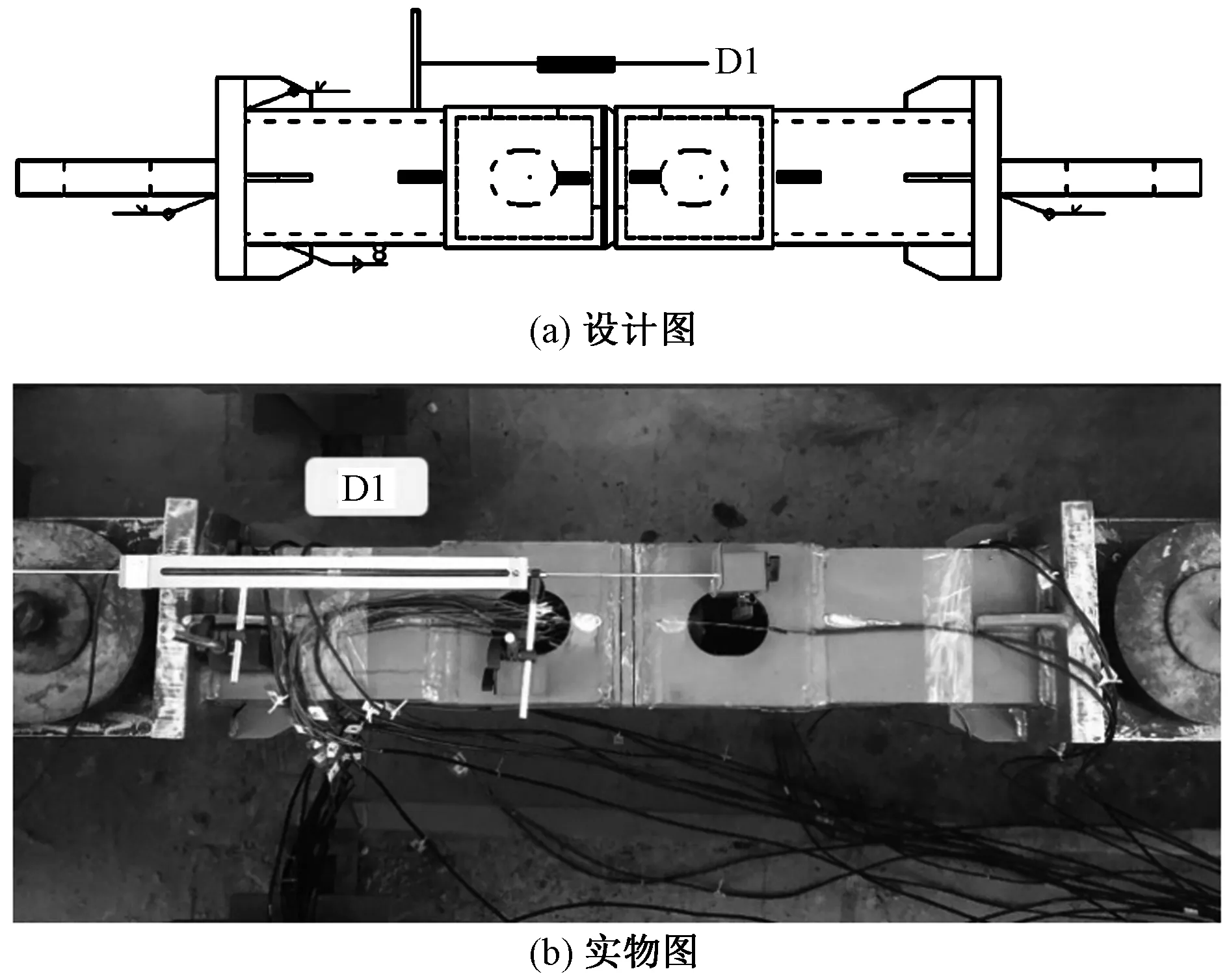
图4 位移计布置图

角件旋转式模块单元连接节点静力抗拉试验应变测量方案如图5及图6所示。分别在上下模块柱靠近角件位置沿模块柱长度方向一周各布置4个应变片，编号依次为1～4，13～16，用以量测节点受拉时，模块柱节点连接区域的受力状态。分别在上下角件靠近连接件位置沿长度方向一周各布置4个应变片，编号依次为5～12，用以量测节点受拉时，角件节点连接区域的受力状态。旋转件中下旋转件螺杆沿长度方向正反两面分别布置2个应变片，编号为17～20；下旋转件底板沿长度方向布置5个应变片，编号为21～25；下旋转件底板沿高度方向上下布置2个应变片，编号为26，27。这些应变片用以量测节点受拉时，下旋转件的受力状态。

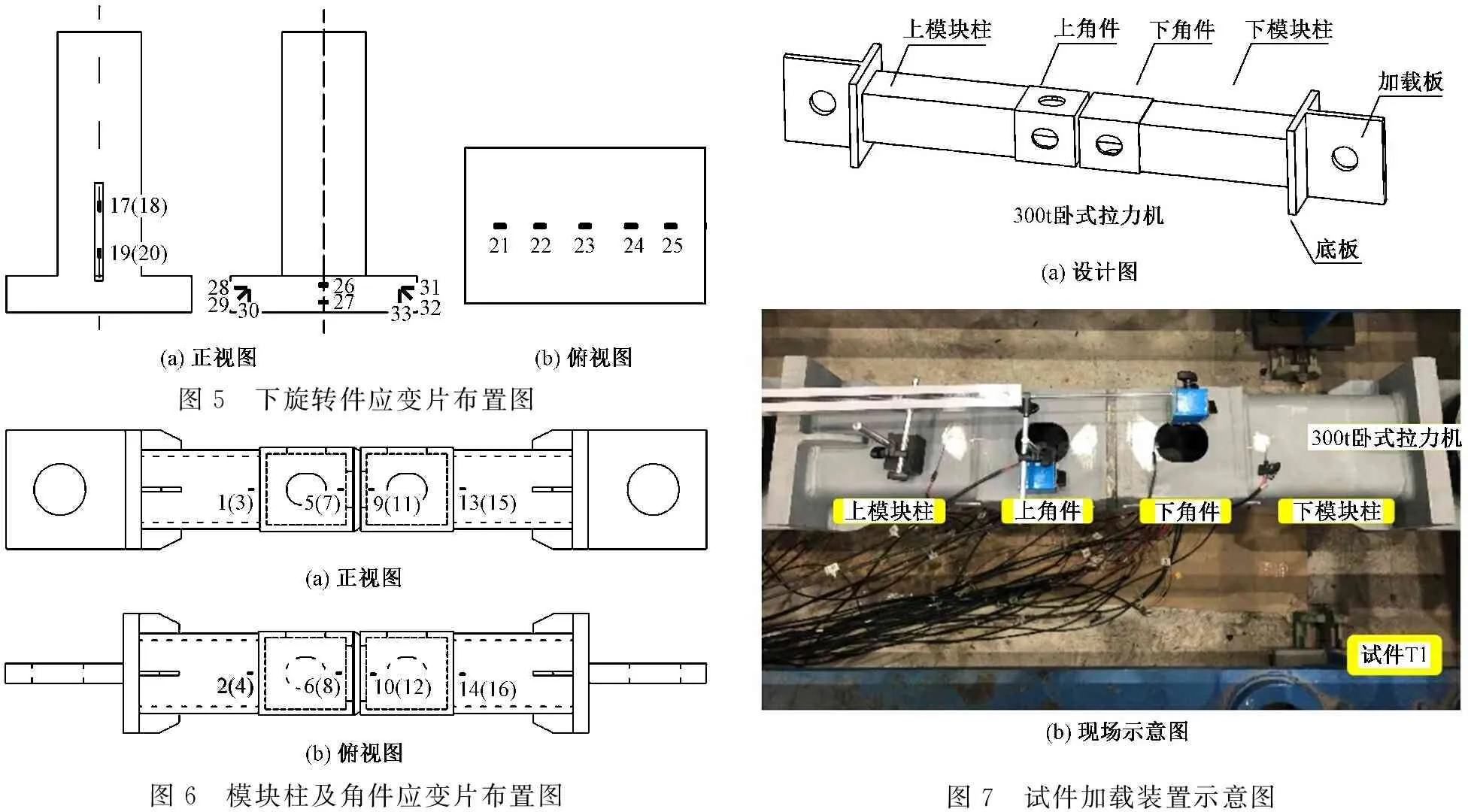
图5 下旋转件应变片布置图图6 模块柱及角件应变片布置图图7 试件加载装置示意图

1.3 试验方案

本试验为静力加载试验，主要考察角件连接节点的基本力学性能，观察其破坏模式。荷载为单向分级加载，根据构件尺寸和实验室条件，抗拉试验加载装置拟采用300t卧式拉力机，试件平放，将试件梁端的带孔耳板固定在拉力机左右夹头中，左右对中后锁死夹头。一端固定，一端施加拉力(图7)。

试验分为预加载阶段和正式加载阶段，预加载的目的主要是使试件各部分接触良好，进入正常工作状态，经过若干次预加载使荷载与变形关系趋于稳定，检查全部试验装置是否可靠，检查全部测试仪器仪表是否工作正常等。在预加载阶段发现问题后需及时调整改进，以保证正式加载阶段试验顺利进行。

预加载采用分级加载的形式，每级加载分两级进行，每级取工作荷载值的20%，然后分两级卸载，加(卸)一级停歇10min。正式加载的前五级每级取工作荷载值的20%，之后每级取工作荷载值的10%直至破坏。为使结构在荷载作用下能够变形充分并达到基本稳定，每级荷载加完后保持5min再采集应变数据。卸载按设计荷载的20%级距进行，卸载完毕20min后，采集测点残余应变数据。在试验过程中，当发生以下现象之一时，即认为节点连接破坏：1)模块柱破坏；2)下角件顶板破坏；3)上角件底板破坏；4)旋转件底板破坏；5)节点部件局部变形过大；6)试件不能继续承载，荷载-位移曲线下降至极限荷载的80%。

1.4 材性试验

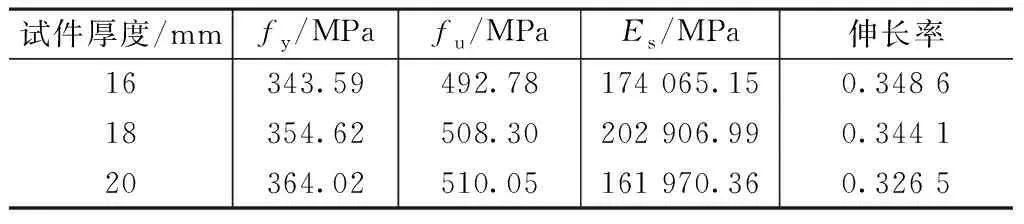
试件中角件及模块柱采用Q345B钢材，连接件中下角件顶板钢材采用G20Mn5QT，旋转部分及螺母钢材采用ZG310-570。通过下述材性试验确定试验中所用钢材在单向拉伸状态下的力学性能参数，包括屈服强度fy、极限抗拉强度fu、弹性模量Es和断后伸长率等。同时也为有限元分析提供精确的钢材材性参数。

本次材性实验按照国家标准《钢及钢产品力学性能试验取样位置及试样制备》(GB/T 2975—1998)、《金属材料室温拉伸试验方法》(GB/T 228—2002)，对模块柱(截面尺寸200mm×18mm)、角件和旋转件进行截取试样并将样胚加工成试件。所有材性试件均与节点试件同期加工，同一母材，试件的表面也经过喷丸除锈处理。每个规格钢板共一组试验，每组试验取3个试样。

材性试验如图8所示，相关力学性能参数测试结果如表1所示。

图8 材性试验图

材性试验结果表1

2 试验结果与分析

2.1 试验现象及破坏模态

试件T1下角件顶板板厚为16mm，T2为20mm，根据有限元模拟和材性试验结果得节点抗拉承载力试件T1约为400kN，T2约为520kN。

约束下模块柱底端，对上模块柱顶端施加轴心拉力。随着荷载增大，出现轻微响声，推断为油漆或焊渣脱落，上下角件与连接板之间出现缝隙，且通过观察可发现下角件与连接板之间的缝隙大于上角件与连接板之间的缝隙。

在试验荷载达到350kN前，试件T1各部件未出现异常，仅上角件与下角件及连接板之间出现缝隙，荷载-位移曲线呈线性关系，所测应变未达到钢材的屈服应变，说明此时试件T1处于弹性阶段，弹性极限荷载为350kN；试件T2的下角件板件较试件T1厚，其弹性阶段延长，弹性极限荷载为450kN。

当试件T1柱端荷载加载值为391kN左右(对应试件T2柱端加载值为527kN)时，伴随着“砰”的响声，下旋转件底板因达到抗剪强度发生断裂，同时柱端荷载迅速回落。无法正常持续加载，试件发生破坏，加载终止。通过观察可以发现下角件与连接板之间缝隙远大于上角件与连接板之间的缝隙，通过测量可以得到，上角件与连接板之间的缝隙约为6mm，下角件与连接板之间的缝隙约为28mm，试验现象如图9、图10所示。

图9 角件旋转式模块单元连接节点试件抗拉试验现象

图10 角件旋转式模块单元连接节点试件抗拉试验图

角件旋转式模块单元连接节点在静力拉伸荷载作用下沿受力方向伸长，结合2.3节中的应变分析可知，当试件破坏时，模块柱和连接板均未达到极限强度，同时上旋转件部分，尤其是螺母以上螺杆部分应力水平较低；下旋转件部分及下角件顶板应力水平较高，除板件边缘外其余区域应力均达到抗拉强度。证明由模块柱传递来的荷载主要依靠上角件底板、下旋转件底板及下角件顶板传递。上角件底部承受由上模块柱传来的拉力，并将拉力传至旋转件，再由下旋转件底板将拉力传递给下角件顶板，最终传递至下模块柱。上角件底板由于受拉变形发生鼓曲，旋转件下部底板发生弯曲变形，且在对应下角件顶板边缘部位明显凹屈，发生凹屈变形的原因为下角件顶板对旋转件的挤压作用产生压力，通过下角件顶板转递至旋转件而引起的板件凹屈。

通过试验可知，节点最终破坏模式为旋转件底板达到抗剪强度引起的剪切破坏。

2.2 试件承载能力分析

抗拉节点承载能力主要从荷载-竖向位移曲线考虑，图11为试件荷载-位移曲线图。试件T1的屈服荷载约为350kN，屈服位移为16mm，而试件T2的屈服荷载为450kN，屈服位移为18mm。试验过程中，试件T2的下角件顶板塑性发展缓慢，与其厚度相关。且最终试件破坏时，试件T1极限荷载为391kN，小于试件T2极限荷载527kN；即下角件板厚增加4mm，极限承载力增大34.78%，说明试件的极限承载力受下角件顶板厚度影响较大，随其厚度增大而增大。

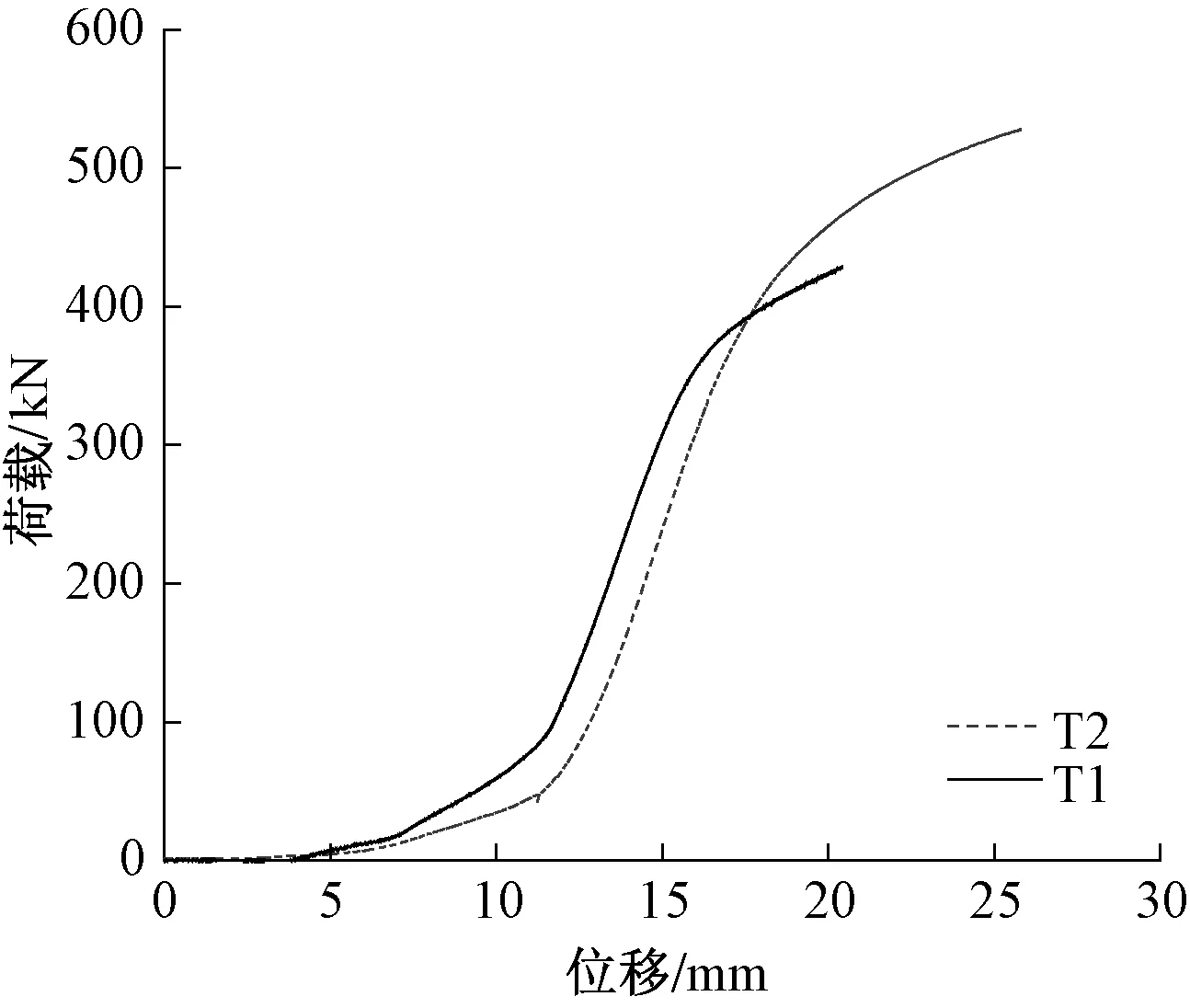
图11 抗拉试验试件荷载-位移曲线

整体荷载-位移曲线呈S形，节点存在屈服后整体刚度强化现象。

2.3 试件应变分析

2.3.1 模块柱及角件应变

模块柱及角件沿柱轴线方向测点的荷载-应变曲线如图12～15所示。

肿头龙脖子短粗，肌肉发达，身体强壮。和很多恐龙一样，肿头龙也长着一条长长的大尾巴，作用就是保持身体的平衡。肿头龙靠后肢站立和奔跑，所以两条后腿的肌肉很发达。与后肢相比，肿头龙的前肢则短得多，爪子上长有五根短短的指头。

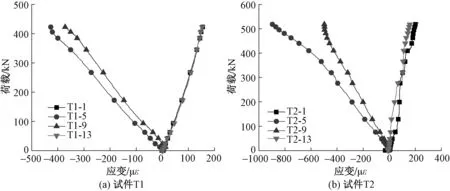
图12 柱轴线方向荷载-应变曲线1

由于1和13，2和14，3和15，4和16测点位于方钢管柱表面的对称位置，试件T1与T2的方钢管柱表面测点的荷载-应变曲线均表现出较好的一致性；同样，位于角件表面的5和9，6和10，7和11，8和12测点曲线也较为一致。由图可以看出，模块柱应变数值较小，均为正值，荷载-应变曲线呈线性发展，可知方钢管柱一直处于弹性受拉状态；角件应变数值较大，均为负值，荷载-应变曲线前期呈线性发展，后期呈非线性发展，角件从弹性受压状态发展为弹塑性受压状态，可知节点在拉力作用下由角件承载主要荷载。

2.3.2 旋转件应变

下旋转件螺杆及底板测点的荷载-应变曲线如图16～18所示。

图16为下旋转件螺杆表面测点的荷载-应变曲线，由图可知，加载过程中，19，20测点的荷载-应变曲线变化趋势相同；加载前期，曲线呈线性关系，螺杆处于弹性变化阶段；当荷载大于弹性极限荷载后，荷载-应变曲线呈非线性变化，且应变值大于屈服应变，螺杆主要起传递荷载的作用。

图17为下旋转件底板表面轴线测点的荷载-应变曲线，由图可以看到，在加载过程中，21，25测点因位于底板端部，应变变化很小；22，23，24测点的荷载-应变曲线变化趋势相同，且位于中部的23号测点应变变化速率及数值均小于22，24测点；相应5个测点的应变为负值，由于底板受弯矩作用，其下表面均处于受压状态，除端部外的3个测点应变均大于屈服应变，且呈现前期增长缓慢，后期快速增长的特点，由此说明随着荷载的逐渐增大，下旋转件底板应力逐渐增大，且中部应力大，端部应力小，节点承载力主要由旋转件底板控制。

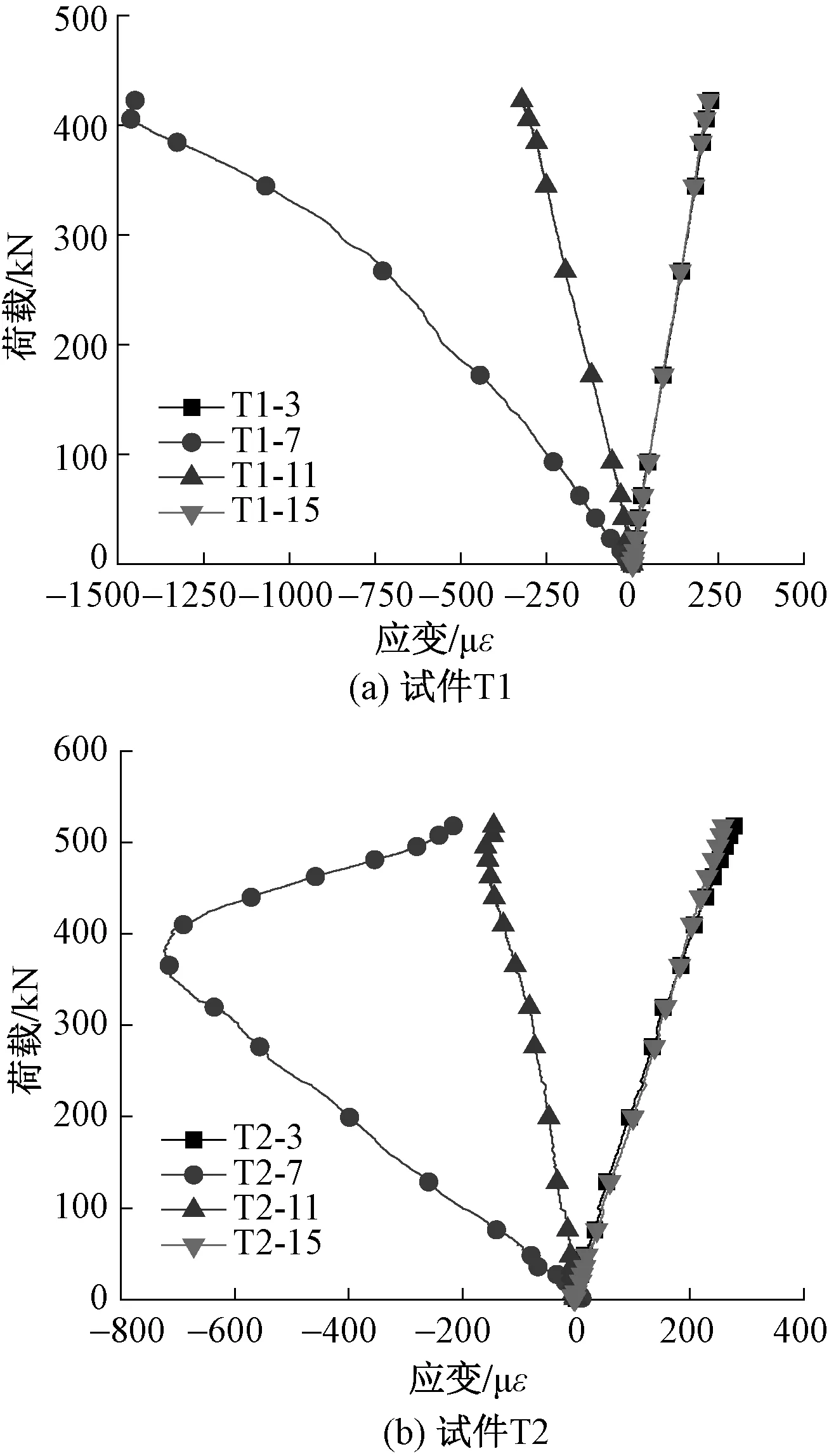
图13 柱轴线方向荷载-应变曲线2

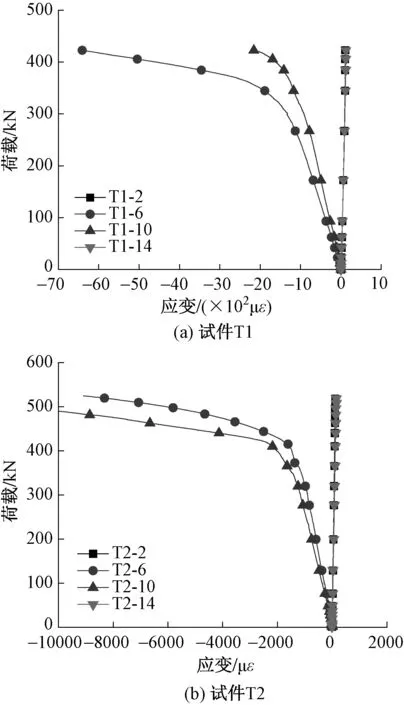
图14 柱轴线方向荷载-应变曲线3

图16 下旋转件螺杆荷载-应变曲线

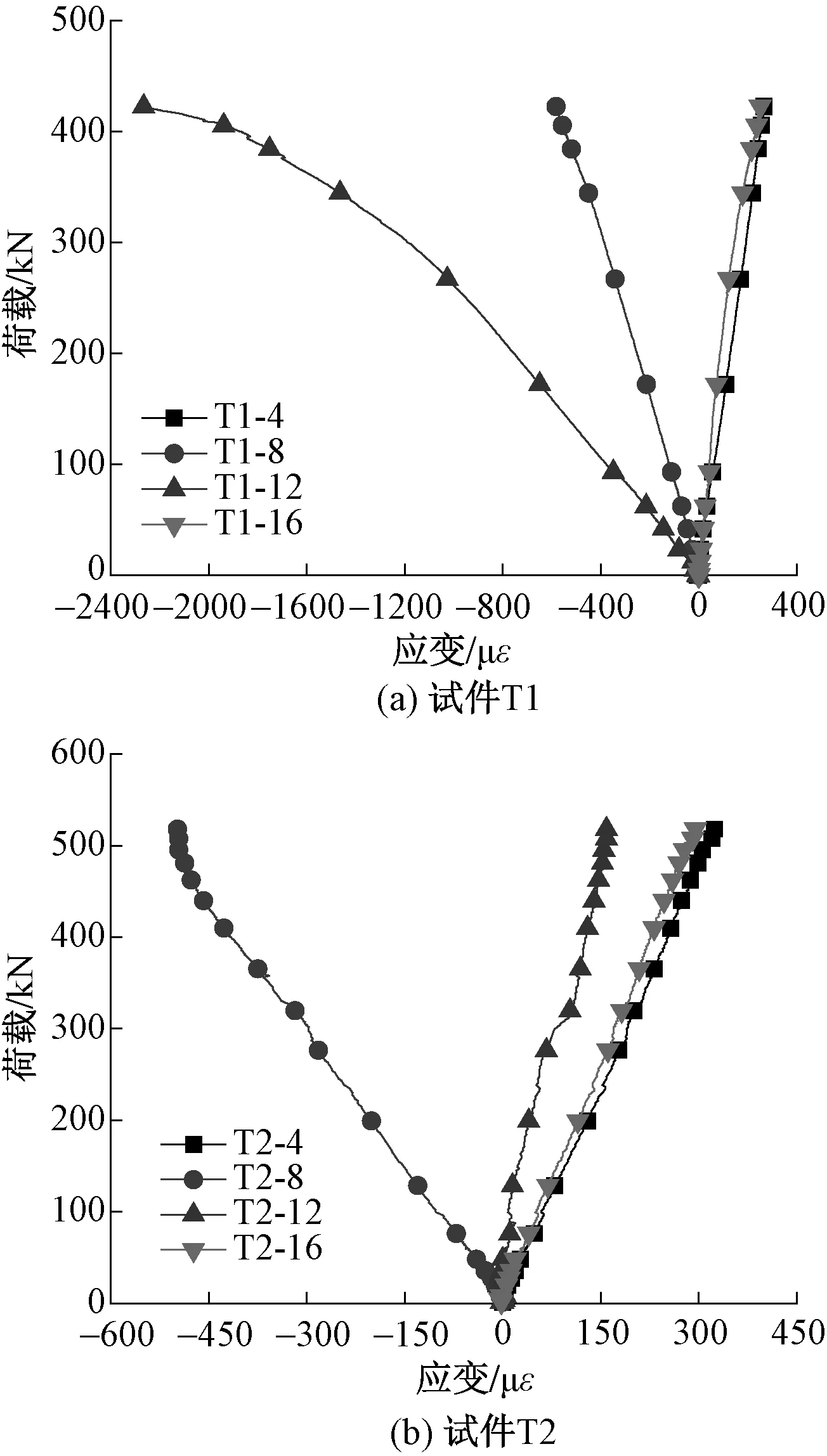
图15 柱轴线方向荷载-应变曲线4

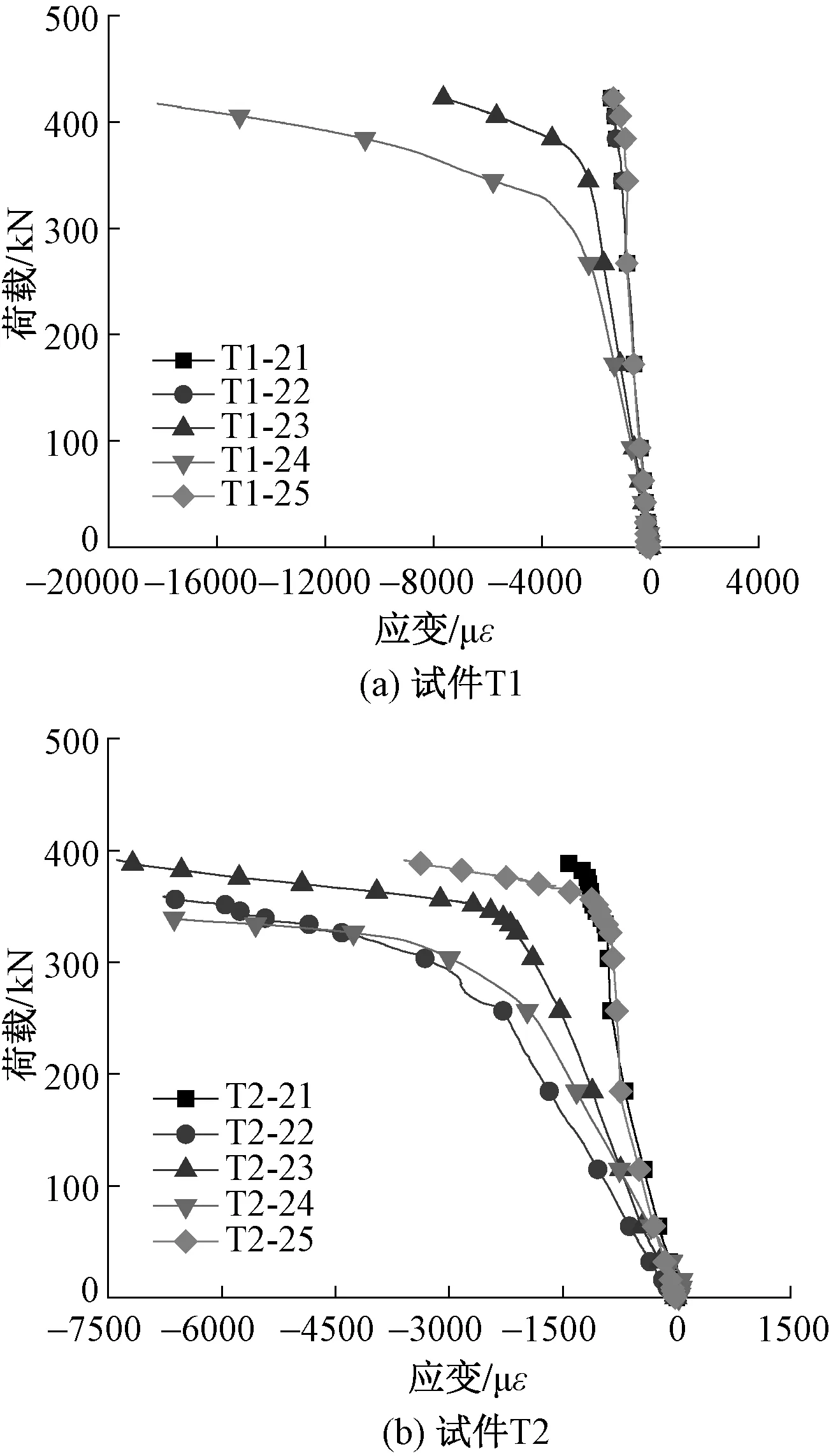
图17 下旋转件底板表面荷载-应变曲线

图18为下旋转件底板侧面中部测点的荷载-应变曲线，由图可知，试件T1与T2的26，27测点荷载-应变曲线呈现较高的一致性，均呈现26测点应变为正值，27测点应变为负值的特点，可知底板侧面上部纤维受拉，下部纤维受压，即节点受拉时，旋转件底板处于受弯状态。

图18 下旋转件底板侧面荷载-应变曲线

3 有限元分析

3.1 模型建立

使用有限元分析软件ABAQUS建立与试验尺寸一致的有限元模型。模型编号为T-1～T-8。模型的部件主要包括：模块柱、下角件、上角件和旋转件，各个部件均采用C3D8R实体单元进行模拟，采用结构化网格划分技术，钢材采用线性强化弹塑性本构模型，角件与模块柱等焊接部位均采用绑定接触，模型如图19所示。

图19 有限元模型

节点有限元模型的节点连接核心区网格划分较密，其他区域的网格划分较为稀疏，节点模型的网格划分如图20所示。

图20 网格划分、边界条件及荷载施加

3.2 边界条件及荷载施加

如图20所示，在角件旋转式模块单元连接节点抗拉有限元模型中，在模块柱端设置参考点RP1和RP2，将参考点RP2与模块柱截面耦合，并对RP2约束三向平动及三向转动。荷载通过参考点RP1以轴向位移的方式施加。

3.3 有限元与试验结果对比

对角件旋转式模块单元抗拉节点进行有限元模拟，得到的破坏模式和试验相似，如图21所示。在角件旋转式模块单元连接节点抗拉初始阶段，节点各部分均处于弹性工作状态，下角件顶板与旋转件底板应力增长较快，且旋转件底板与螺杆交界处的应力明显高于其他位置；随着竖向位移继续增大，荷载逐渐增加，下角件顶板及旋转件底板出现屈服并不断扩展；竖向位移继续增大，旋转件底板屈服并出现剪切破坏；数值模拟中相应位置应力达到屈服。说明数值模型可以有效地模拟出角件旋转式模块单元连接节点在拉力作用下的破坏模态。

图21 有限元与试验对比图

图22为试验与有限元分析的荷载-位移曲线对比。由图可知，有限元模拟曲线与试验曲线的发展趋势比较吻合。表2为试验与有限元的承载力值，模型T-1与试件T1的极限承载力误差约为0.44%，模型T-2与试件T2的极限承载力误差约为0.24%，误差较小，误差的产生主要在于有限元模拟中未考虑焊缝影响，同时试件存在一定的加工误差和缺陷。总的来说有限元模拟结果基本能够反映角件旋转式模块单元连接节点试件实际受力情况。

图22 荷载-位移曲线对比图

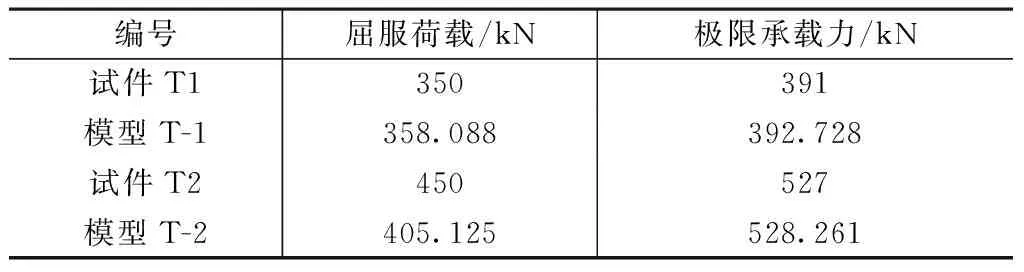
试验与有限元结果对比表2

3.4 参数化分析

3.4.1 下角件顶板厚度的影响

通过有限元分析得到各角件旋转式模块单元连接节点模型的极限承载力和屈服承载力，屈服承载力用整体屈服法确定，依据节点荷载-位移曲线，将初始线性段的延长线与斜率近似为常数的非线性段的切线相交处定义为模型的屈服承载力。对比结果列于表3。

模型参数及承载力汇总表3

随下角件顶板厚度增加，节点抗拉极限承载力增大，且随其厚度增大，承载力提升效果越来越不显著，综合考虑经济性，建议选取顶板厚度20mm。

在单调静力荷载作用下，各模型的应力云图变化规律基本一致，以模型T-2为例进行分析。图23为模型T-2在静力荷载作用下的应力云图，模型最大应力发生在下角件顶板以及旋转件底板和上角件底板，连接板及方钢管应力相对较小，极限承载力状态下，表现为下角件顶板受拉屈服，旋转件底板受拉屈服。

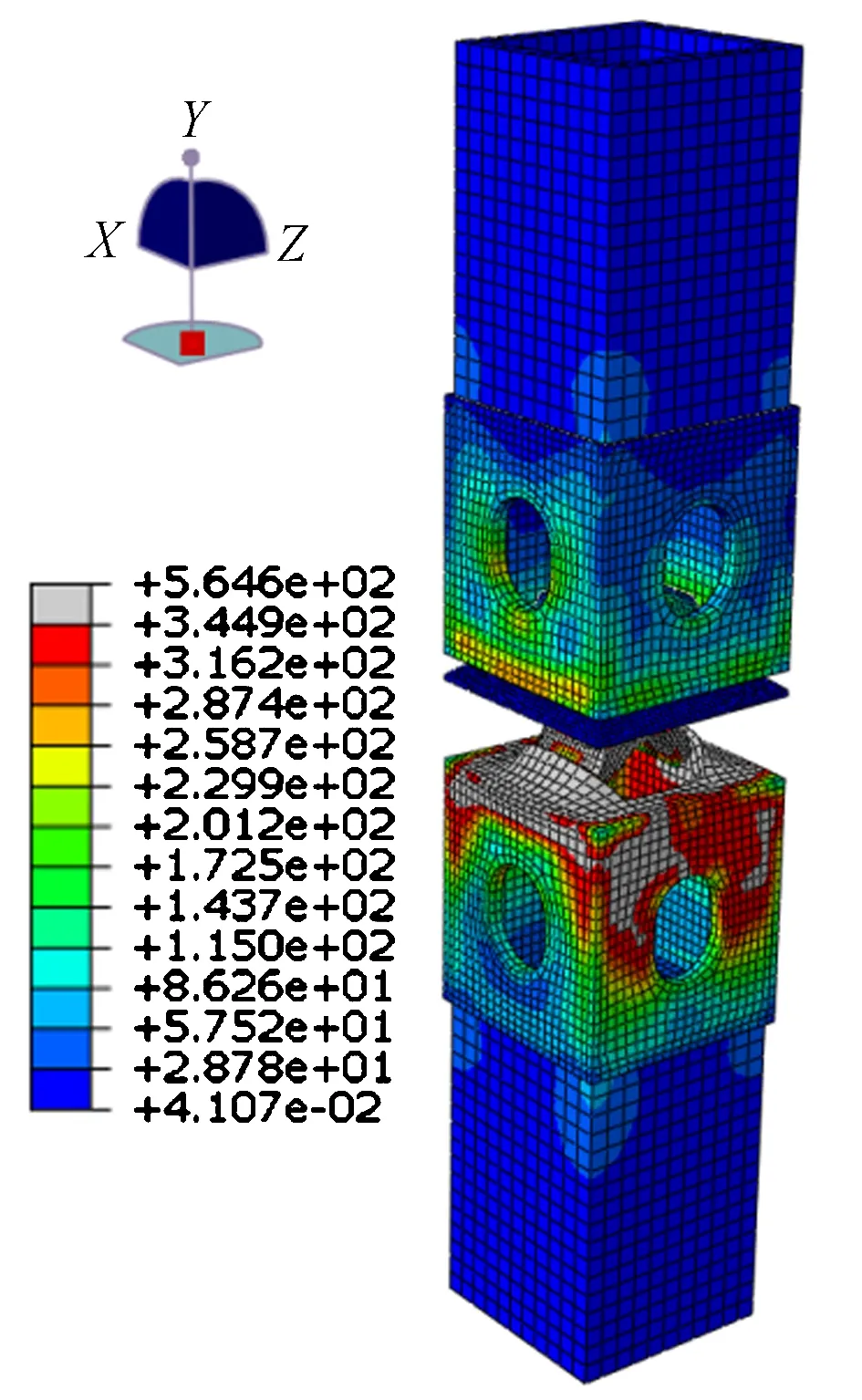
图23 模型T-2应力云图/MPa

提取下角件变形云图如图24所示，下角件在轴向拉伸荷载作用下发生鼓曲变形，发生鼓曲变形的原因是拉力通过旋转件传递到下角件，引起下角件顶板鼓曲。为深入研究下角件顶板的变形规律，提取沿顶板上表面平行于Z轴方向的中轴线上变形规律如图25所示。关键点分别为对应中轴线两侧端点与对应中轴线洞口边缘两点，其他条件相同下，板件厚度递增，模型T-4与模型T-1相比，对应中轴线洞口边缘两点变形量减小29.62%，随着下角件顶板板厚增加，顶板洞口两端的竖向变形减小。原因在于下角件顶板厚度增大，节点刚度增大，在相同荷载下，节点的变形相对减小。