蒙古国Eco Tower钢结构中美规范设计对比分析

金天德， 丁 斌

(杭州市城建设计研究院有限公司， 杭州 310020)

0 引言

中美两国规范在设计理念及相关规定上有较多差异，学者们从多个方面对两国规范进行了对比。罗开海等[1]、朱文静等[2]、顾强等[3]针对中美规范地震动参数的转换、地震作用计算方法及钢结构的水平地震作用方面进行了对比研究。黄韬颖[4]、张军锋等[5]对中美风荷载规范及风荷载标准值进行了对比分析。陈绍蕃[6]、梁德勇[7]对中美钢结构规范及钢构件设计方法进行了比较。但目前针对中美规范在钢结构高层实际项目中比较全面的对比分析较少。

本文分别运用中、美两国规范对蒙古国Eco Tower钢结构高层项目进行设计，剖析两者在荷载取值、分析方法和构件设计等方面的差异。

1 工程概况

Eco Tower钢结构项目位于蒙古国首都乌兰巴托，地下2层、地上52层(1～7层为裙房)。塔楼结构平面呈四边形，短边25.5m，长边34.487～39.923m，斜边24.167m(图1～3)。底层层高4.2m，其余裙房层高3.6m，标准层主要层高3.45m，个别办公层高4.0m，主体结构高度为187.9m，地上主楼总建筑面积约为70 000m2。其中裙房部分主要功能为商业，塔楼主要功能为办公、酒店。

图1 三维模型效果图

2 结构体系

主楼采用钢框架-中心支撑结构体系。外框采用钢框架，内筒在建筑有墙体位置X，Y两个方向各设置越层中心支撑4片(图2、图3)。内外筒间距8.5～8.6m，外框柱距5.5～8.5m。外框柱采用圆钢管混凝土，截面为φ1 000×45～φ500×16(C60～C40)，内筒柱采用矩形钢管混凝土柱，截面为□1 200×1 200×80×80～□500×500×20×20(C60～C40)。箱形支撑，截面为□500×400×45×45～□300×300×16×16，主、次梁采用H形钢梁，其中主梁截面为H800×400×20×40～H500×200×10×16，楼板板厚为120mm。

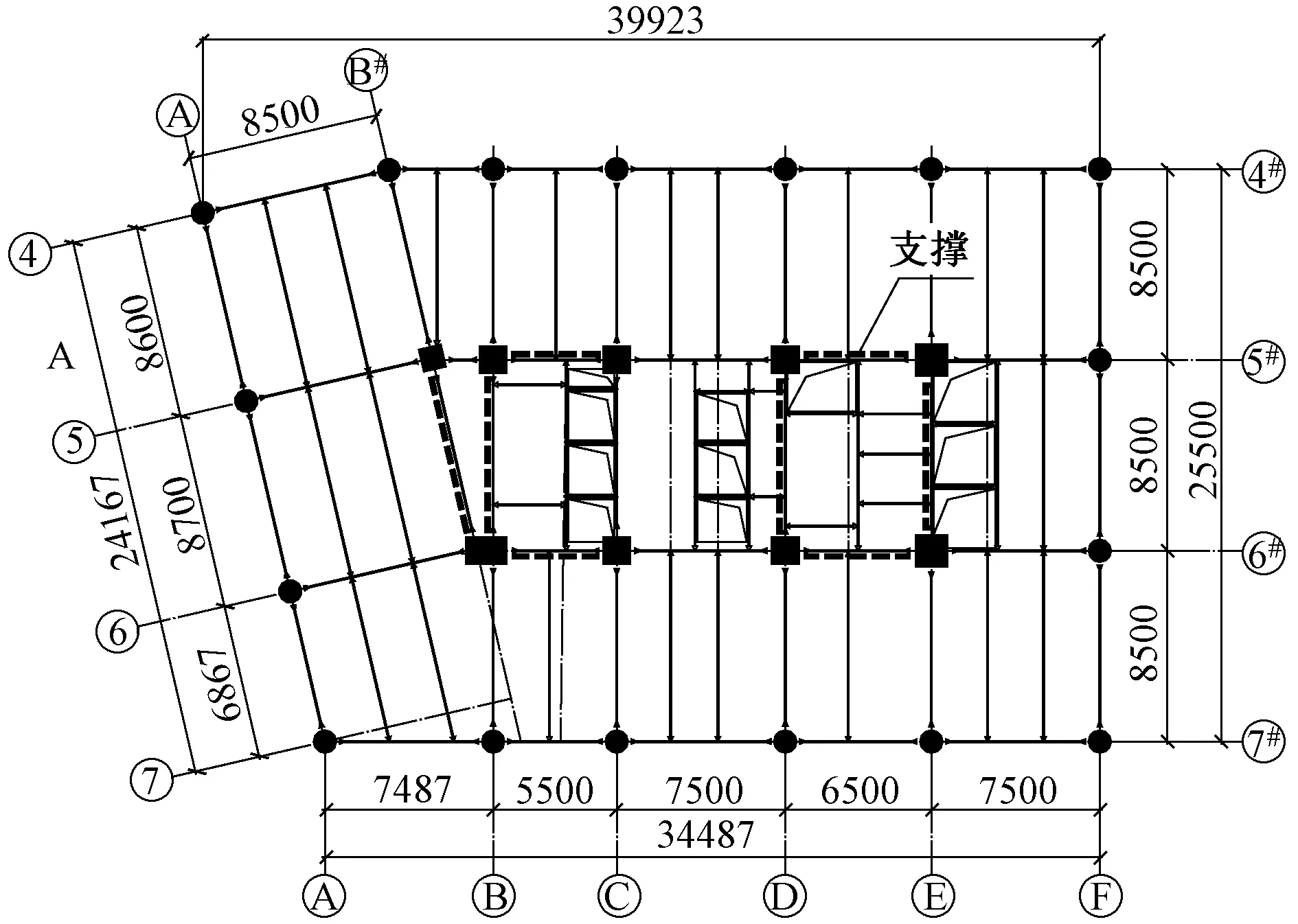
图2 结构平面图

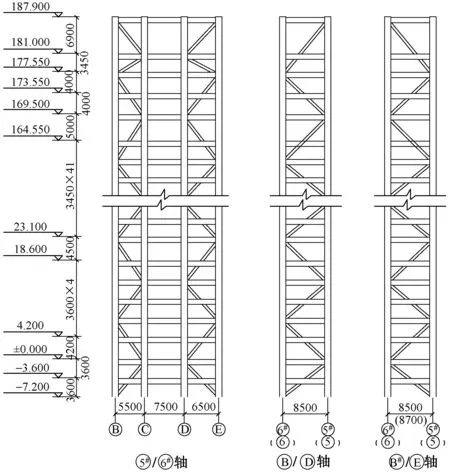
图3 支撑立面图

3 模型材料和荷载对比

采用两个构件截面、恒荷载、约束条件及基本假定等均相同的模型进行对比分析。但两个模型的材料弹性模量、材料强度、质量源、活荷载、风荷载、地震荷载、设计参数分别按美国、中国规范选取，构件设计及控制指标也分别按各自规范进行。

3.1 混凝土(用于钢管混凝土柱内及楼面)

美国规范ACI 318-11[8]采用圆柱体抗压强度平均值f′c进行设计。

中国规范GB 50010—2010[9]以边长150mm立方体抗压强度标准值fcu,k为基础，再通过公式0.88αc1αc2fcu,k/1.4(式中：αc1为棱柱强度与立方强度比值；αc2为脆性折减系数；1.4为抗力分项系数)得到轴心抗压强度设计值fc。

中美规范对应的弹性模量Ec分别按式(1)及式(2)进行计算。

(1)

(2)

式中f′c为规范规定的混凝土抗压强度。

以同等条件下强度相等原则，进行不同规范混凝土的转换[10]。本项目采用的主要的混凝土强度设计取值及弹性模量如表1所示。

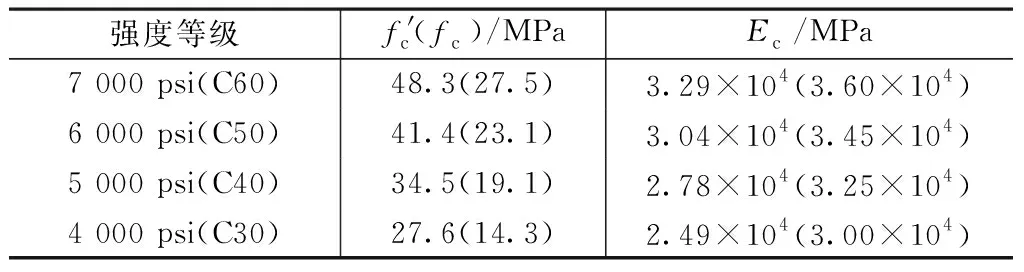
两个模型对应采用的混凝土材料特性 表1

同等强度条件下，相对美国规范模型，混凝土弹性模量中国规范模型取值略大10%～20%。柱内混凝土从底到顶中国规范模型采用C60～C40，美国规范模型采用7 000～5 000psi。中美两国规范模型中楼板混凝土分别采用C30，4 000psi。

3.2 钢材

美国规范ANSI/AISC 360-10[11]中，50级钢材屈服强度345MPa，55级钢材屈服强度380MPa，中国规范GB 50017—2017[12]对应钢材等级Q355(屈服强度345MPa)，Q390(屈服强度390MPa)。

钢材弹性模量取值，美国规范Es=2×105MPa，中国规范Es=2.06×105MPa，中国规范取值略大3%。

中国规范模型除底部几层内筒柱采用Q390以外的所有柱、支撑及梁均用Q355，对应美国规范模型采用55级及50级钢材。

中国规范强度设计值为屈服强度除抗力分项系数即f=fy/1.125。美国规范强度设计值直接取屈服强度fy，而抗力系数则在承载力计算时根据受力状态进行区分。承载力设计值为φRn(其中Rn为承载力标准值，φ为抗力系数)，φ根据受力状态不同情况取值不同(钢结构构件一般取0.9，但组合构件受压时取0.75)。对于强度设计值控制要求，两国规范基本相当。

4 本项目中美规范的主要参数对比

4.1 结构整体参数

中美两国规范模型采用的结构整体参数见表2、表3。

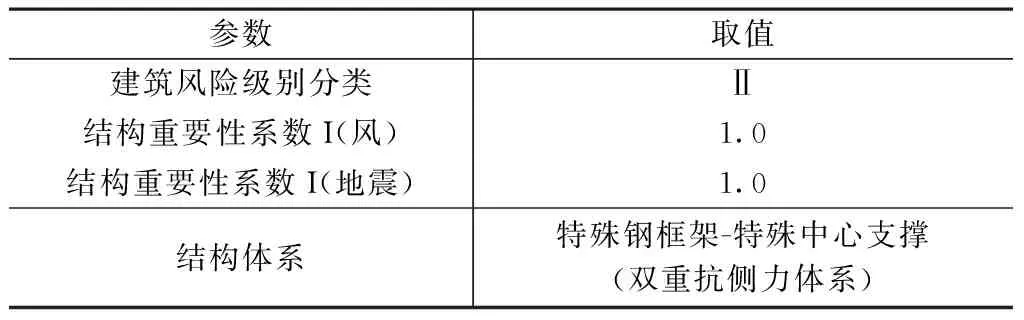
美国规范模型采用整体参数 表2

中国规范模型采用整体参数 表3

美国规范[13]基于建筑抵御自然灾害的风险对建筑进行分级(Ⅰ～Ⅳ级)。根据不同分类，针对风、雪、冰、地震荷载给出不同重要性系数。

中国规范GB 50009—2012[14]，GB 50011—2010[15]等基于建筑破坏可能产生后果的严重性对建筑分类(安全等级分为一～三级，抗震设防分类分为甲～丁类)。活荷载、风荷载、雪荷载工况根据安全等级乘以对应的结构重要性系数。地震工况则是根据设防分类调整抗震措施或抗震构造措施。

4.2 活荷载

中美两国规范差别不大，整体美国规范ASCE/SEI 7-10略大，本项目设计涉及的活荷载如表4所示。

4.3 风荷载

中美规范在重现期、粗糙度、体型系数、高度系数及风压计算均存在不同程度差异。主要体现在以下几个方面：

4.3.1 重现期

中国规范GB 50009—2012重现期50年(风敏感结构为100年)。

中美规范主要的活荷载对比/(kN/m2) 表4

美国规范ASCE/SEI 7-10重现期为300～1 700年不等，但对应分项系数为1。本项目风险级别分类为二级，对应重现期取700年。

4.3.2 风压公式

美国规范ASCE/SEI 7-10设计风压p(超高层周期较长，为柔性结构)：

p=qGfCp-qi(GCpi)

(3)

基本风压qz：

qz=0.613KzKztKdV2

(4)

式中：q为高度z处基本风压；Gf为阵风系数；Cp为体型系数；qi为内部压力；GCpi为内压系数；Kz为高度系数；Kzt为地形系数；Kd为风向系数；V为基本风速。

中国规范GB 50009—2012风荷载标准值wk：

wk=βzμsμzw0

(5)

基本风压w0：

(6)

式中：βz为阵风系数；μs为体型系数；μz为高度系数；v0为基本风速。

4.3.3 基本风速

中美两国规范基本风速的离地高度均取10m；记录时距，中国规范GB 50009—2012自记10min平均年最大风速，美国规范ASCE/SEI 7-10为3s。

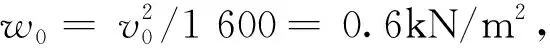
美国规范ASCE/SEI 7-10表C6-2，换算时距3s的平均最大风速V3=1.427×31=44.24m/s，根据公式(C26.5-2)，50年一遇风速换算为700年一遇风速为V700/V3=[0.36+0.1ln(12T)]=1.264(式中T为换算后重现期，此处取700)，故V700=55.9m/s(700年一遇)。

4.3.4 高度系数

美国规范ASCE/SEI 7-10：

(7)

式中：zg为梯度风高度；α为风速剖面指数。当地面粗糙度为C时，zg取274.32m，α取9.5。

中国规范GB 50009—2012：

μz=μ10(z/10)α

(8)

式中μ10为高度变化系数，当地面粗糙度为B时，μ10取1.0，α取0.3(美国规范ASCE/SEI 7-10中地面粗糙度C与中国规范GB 50009—2012地面粗糙度B相当)。

4.3.5 体型系数

美国规范ASCE/SEI 7-10：体型系数Cp正风向0.8，背风向-0.2，内压系数GCpi=±0.18。

中国规范GB 50009—2012：体型系数为1.4(正风向0.8，背风向-0.6)。

4.3.6 风振及阵风系数

美国规范ASCE/SEI 7-10采用阵风系数，本项目周期较长，根据美国规范ASCE/SEI 7-10柔性结构阵风系数Gf计算公式(式(9))推算出X,Y两个方向的风系数1.102，1.091。

(9)

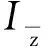
中国规范GB 50009—2012采用风振系数：

(10)

式中：I10为10m高度名义湍流强度；g为峰值因子,取2.5；R为脉动风荷载的共振分量因子；Bz为脉动风荷载的背景分量因子。

4.3.7 风载主要参数

中美两国规范模型采用的风荷载参数见表5、表6。

4.4 地震荷载

美国规范ASCE/SEI 7-10采用的全国地震动参数MCE是基于重现期为2 475年(即50年超越概率为2%)，而设计的加速度仅取MCE的2/3(相当于我国的中震)。采用单一阶段设计步骤实现其设防目标，同时通过引入不同结构体系的反应调整系数R体现结构的延性，再根据不同体系的Ω0(超强系数)、Cd(位移放大系数)进行截面抗震承载力验算和抗震变形验算。

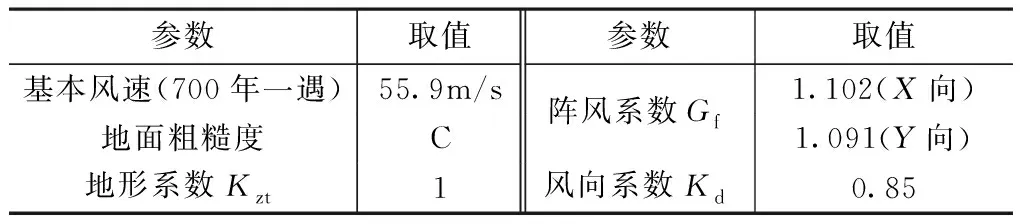
美国规范模型采用风载参数 表5

中国规范模型采用风载参数 表6

中国规范GB 50011—2010采用两阶段步骤来实现小震不坏，中震可修，大震不倒的“三水准”的目标。

4.4.1 反应谱

本工程中美规范反应谱如图4所示。

图4 本工程中美两国规范反应谱曲线

美国规范ASCE/SEI 7-10反应谱大致相当于中国规范GB 50011—2010中震水平，当考虑R系数后，远小于中国规范GB 50011—2010。

4.4.2 质量源

美国规范ASCE/SEI 7-10，质量源为全部自重标准值和仓储部分的活荷载、长期设备荷载及部分雪荷载(普通活荷载不考虑)。

中国规范GB 50011—2010，质量源为全部自重标准值和活荷载组合值(普通活荷载组合值为0.5)。

美国规范ASCE/SEI 7-10质量源略小于中国规范GB 50011—2010。

4.4.3 地震参数

根据业主提供安评报告，50年超越概率10%的地面加速度为191cm/s2(设计考虑为200cm/s2)，换算成中国规范为8度0.2g。安评报告未给50年超越概率2%的地面加速度值，参考中国规范GB 50011—2010中8度罕遇地震作用下50年超越概率2%与50年超越概率10%峰值加速度比值γCN=2.25，根据美国规范ASCE/SEI 7-10，得出MCE短周期谱反应加速度值Ss：

Ss=2.5Apga=2.5×2.25×0.2=1.125

式中Apga为超越概率2%的地面加速度值。

文献[1]给出了特征周期Tg与S1，Ss的对应公式：

Tg=(FvS1)/(FaSs)[1]

式中Fv，Fa为场地调整系数。

根据特征周期Tg=0.35s，计算得MCE1s周期谱反应加速度值S1=0.255，模型计算地震主要参数如表7、表8所示。

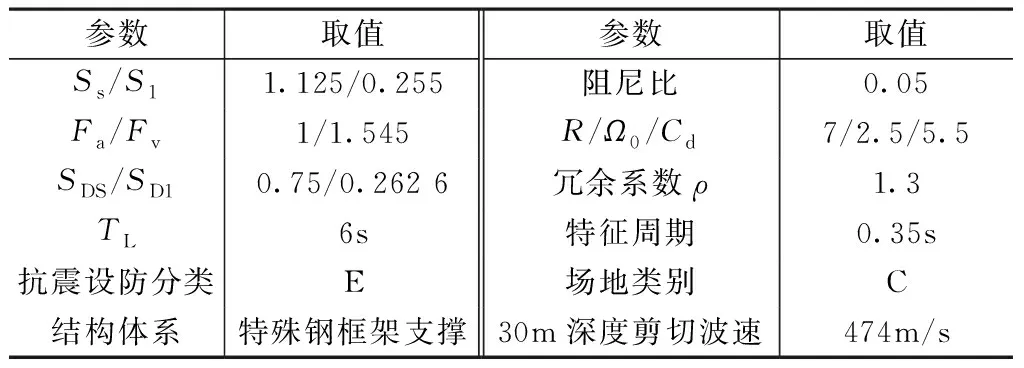
美国规范模型采用地震参数 表7

中国规范模型采用地震参数 表8

5 整体内力分析

5.1 整体计算

本工程主要周期计算结果如表9所示，中美规范模型主要周期结果差别仅1.6%。

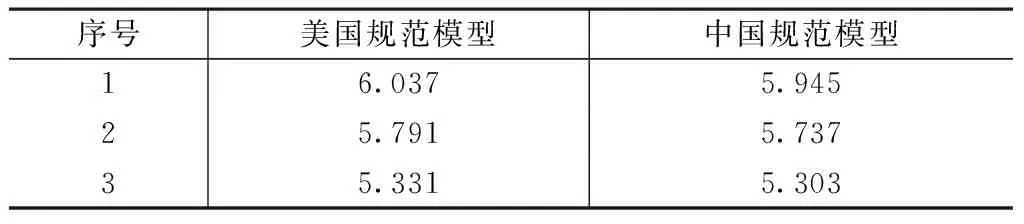
中美规范模型主要周期结果/s 表9

本项目为钢结构且仅考虑弹性分析，偏差由美国规范ASCE/SEI 7-10与中国规范GB 50011—2010两个规范要求的质量源及弹性模量不同引起。

中国规范JGJ 99—2015[16]中考虑楼板刚度规定梁放大系数考虑1.5(边梁1.2)，本次对比分析时美国规范模型也相同处理。

5.2 地震及风荷载作用基底剪力对比

按美国规范ASCE/SEI 7-10考虑R系数以后及中国规范GB 50011—2010计算得到的地震作用下嵌固端剪力如表10所示。

地震作用下嵌固端剪力/kN 表10

美国规范ASCE/SEI 7-10计算得到的地震作用下嵌固端剪力不考虑R时X向和Y向分别约为中国规范GB 50011—2010的2.36倍和2.50倍，接近中国规范GB 50011—2010“中震”。在考虑系数R=7后X向和Y向计算结果约为中国规范GB 50011—2010的34%，36%，远小于中国规范GB 50011—2010小震水平，即使构件计算时考虑Ω0或ρ放大后，仍远小于中国规范GB 50011—2010计算内力。

风荷载作用下两国规范计算得到的嵌固端剪力如表11所示。

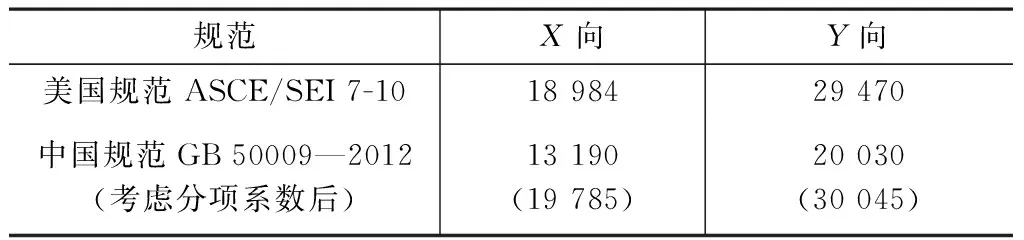
风荷载作用下嵌固端剪力/kN 表11

中国规范GB 50009—2012考虑分项系数1.5后，两国规范计算得到的嵌固端剪力比值非常接近，中国规范GB 50009—2012底层剪力略大，X,Y两个方向分别大4%和2%。

5.3 层间位移角对比

根据美国规范ASCE/SEI 7-10，地震作用下层间位移角计算需放大Cd=5.5，放大后的地震力约为中国规范GB 50011—2010中震水平，对应层间位移角限值为1/50。

中国规范CECS 159—2004规定风和小震作用下层间位移角均为1/300，而大震作用下限值为1/50。

风荷载和多遇地震作用下结构位移见表12。

风荷载和地震作用下结构层间位移角 表12

美国规范ASCE/SEI 7-10计算层间位移角时，考虑系数Cd放大后的地震力基本与中国规范GB 50011—2010中震相当，但位移角限值与中国规范GB 50011—2010大震要求一样。美国规范ASCE/SEI 7-10对变形的控制要求，相对中国规范CECS 159—2004更宽松。层间位移角对比如图5、图6所示。

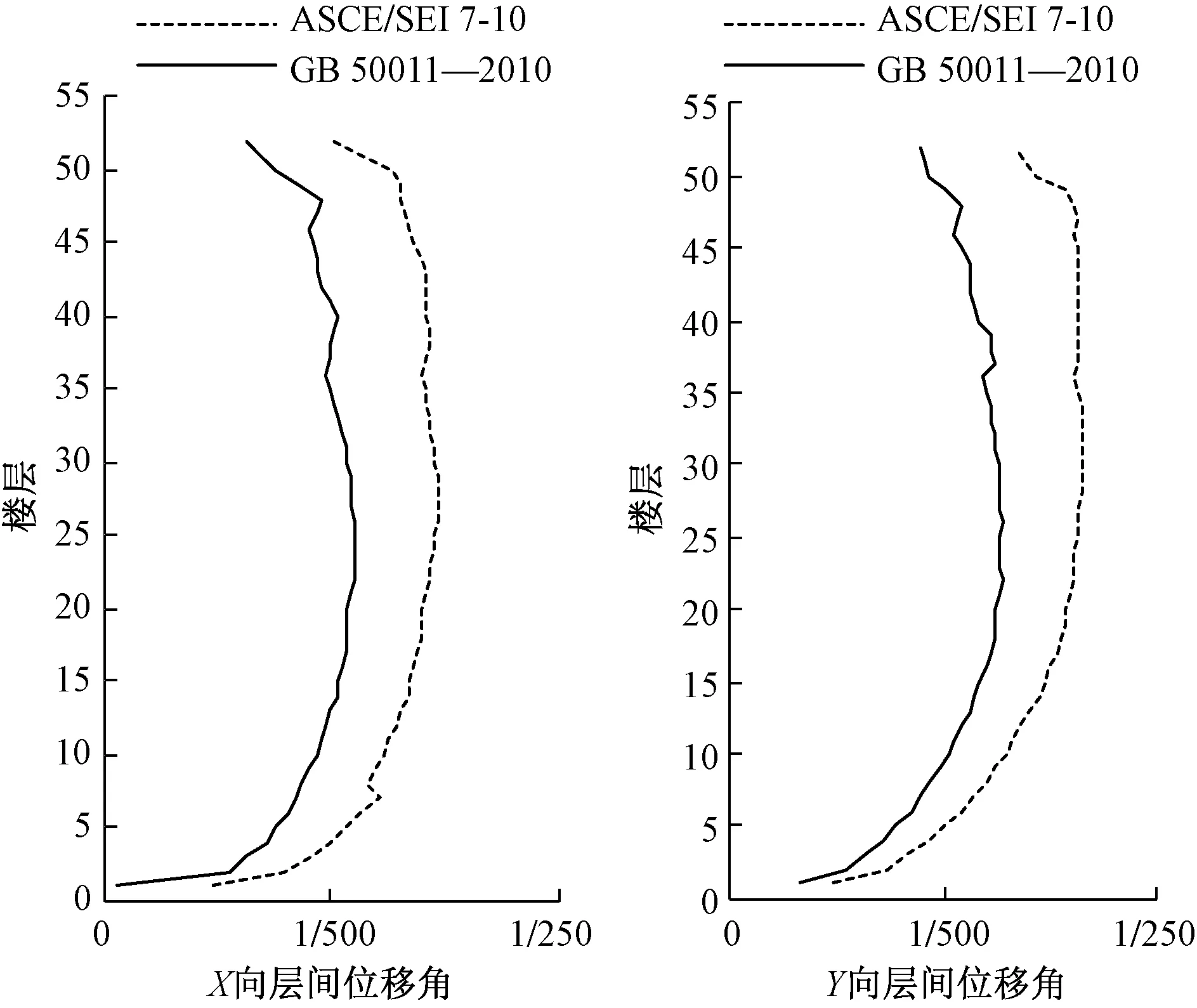
图5 地震作用下最大层间位移角曲线

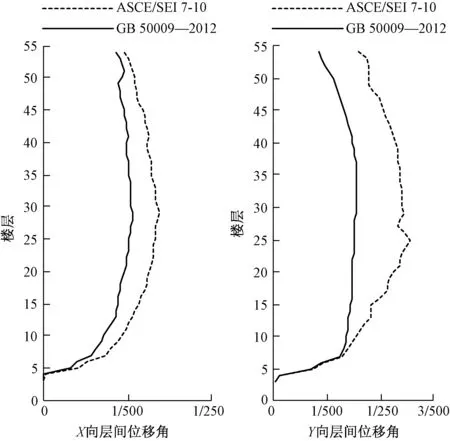
图6 风荷载作用下最大层间位移角曲线

5.4 层间侧向刚度比对比

中美两国规范对层间侧向刚度比(竖向规则性)要求基本一致，美国规范ASCE/SEI 7-10要求楼层抗侧移刚度小于上层的70%或小于上面三层平均抗侧移刚度的80%；中国规范JGJ 99—2015框架结构要求同美国规范ASCE/SEI 7-10，但对于钢框架-支撑结构，采用考虑层高修正的侧向刚度比时，要求不小于上一层的90%。

本项目抗侧刚度的算法，美国规范ASCE/SEI 7-10层间侧向刚度比为层间位移角比：

中国规范为考虑层高修正侧向刚度比：

式中：i为第i楼层；θi,θi+1为第i，i+1层层间位移角；Δi，Δi+1为第i，i+1层地震剪力标准值作用下的层间位移；hi，hi+1为第i，i+1层层高；Vi，Vi+1为第i，i+1层地震剪力标准值。

层间侧向刚度比公式中美两国规范不同，计算结果对比见图7，两者略有差异。本项目竖向刚度比较均匀，差异比较小，均能满足各自规范要求。

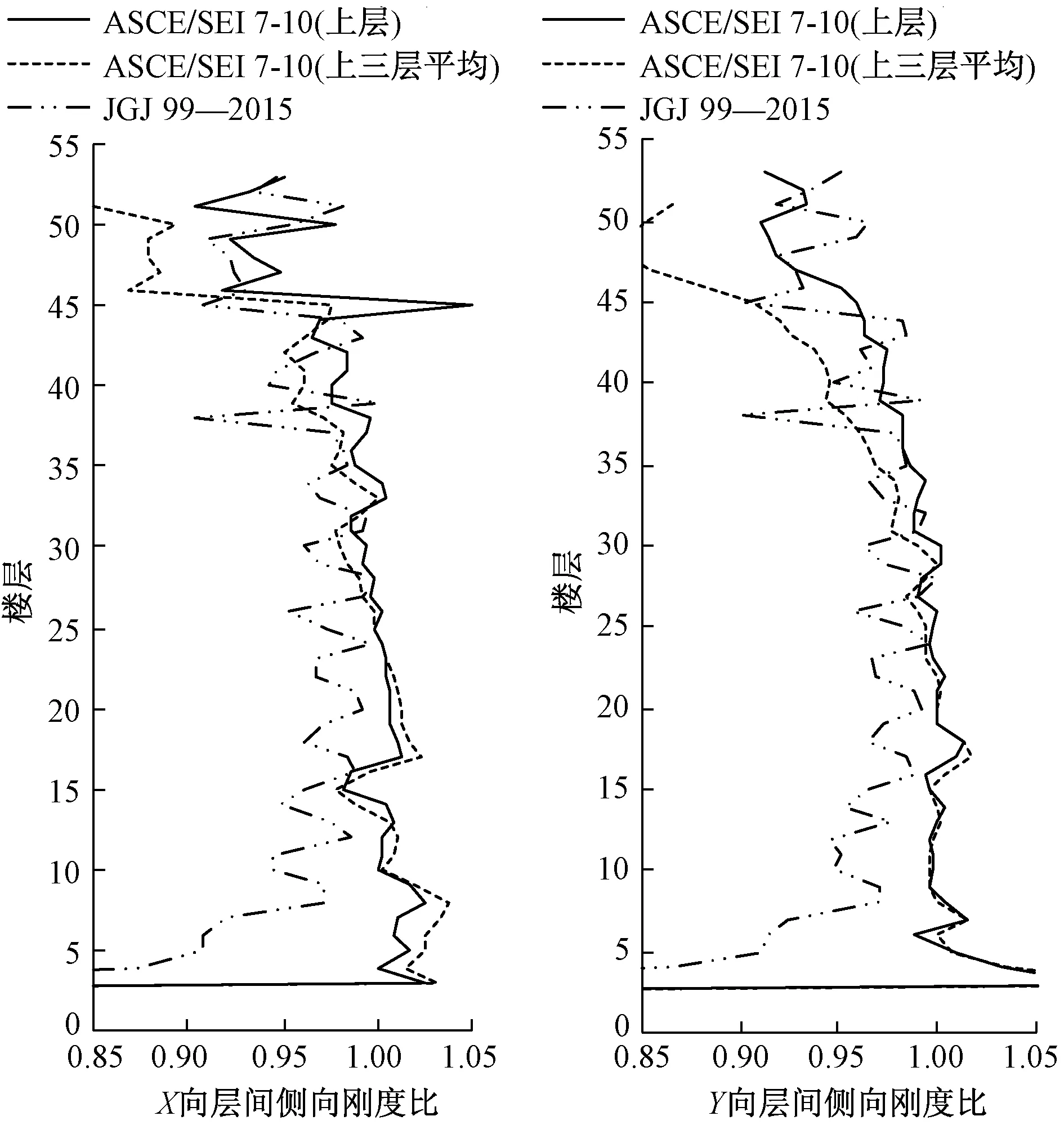
图7 层间侧向刚度比曲线

5.5 二阶效应系数对比

美国规范ASCE/SEI 7-10公式：

(11)

式中：θ为二阶效应系数；θmax为二阶效应系数允许最大值；Px为在x层以上总的竖向力；Vx为x和x-1层之间的地震层剪力(楼层总水平力)；Δ为在Vx作用下的楼层层间位移；hsx为x层层高；β为x层和x-1层之间剪切要求和剪切能力的比值，取1。

中国规范GB 50011—2010公式：

(12)

式中：∑N为考虑楼层以上所有竖向荷载之和；∑H为考虑楼层总的水平力；Δu为考虑楼层层间位移；hi为第i层层高。

两国规范公式式(11)和式(12)基本一致，竖向力的取值略有不同，美国规范ASCE/SEI 7-10要求各荷载系数不超过1，中国规范GB 50011—2010取设计值。计算采用屈曲分析，荷载取值按各自规范，结果见表13。

屈曲因子 表13

两国规范计算结果的差别主要由荷载系数引起，中国规范GB 50011—2010二阶效应系数略偏大。

6 构件分析对比

6.1 中美规范荷载组合及构件计算公式

6.1.1 美国规范ASCE/SEI 7-10荷载组合

美国构件设计分为分项系数法(LRFD)与容许应力法(ASD)两种，其中分项系数法与我国规范GB 50009—2012相似，因此主要细述分项系数法的荷载组合。

美国规范ASCE/SEI 7-10主要规定了以下组合：1)1.4D；2)1.2D+1.6L；3)1.2D+(L或W)；4)1.2D+1.0W+L；5)(1.2+0.2SDS)D+1.0E+L；6)0.9D+1.0W；7)(0.9-0.2SDS)D+1.0E。其中D为恒荷载；L为活荷载；W为风荷载；E为地震作用。

6.1.2 中国规范GB 50009—2012和GB 50011—2010荷载组合

(13)

S=γGSGE+γEhSEhk+γEvSEvk+φwγwSwk

(14)

式中：i，j为荷载种类数；γG(γGi)，γQ1(γQj)，γEh(γEv)，γw分别对应恒荷载、活荷载、水平(竖向)地震、风荷载的分项系数；SGE(Gik)为恒荷载；Qi1k(Qjk)为活荷载；SEhk，SEvk为竖向和水平向地震；γLj为设计使用年限调整系数；φcj(φw)为组合系数。

6.1.3 中美规范构件计算公式的区别

本项目构件主要为梁(纯弯)、支撑(轴压)、柱(压弯)，对应承载力计算公式如下：

美国规范AISC 360-10：

Mx≤φbMP=φbFyZx

(15)

N≤0.9Pn=0.9FcrAg

(16)

(17)

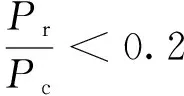
(18)

式中：φb为抗力系数；Fy为钢材屈服强度；Zx为X轴塑性截面模量；Fcr为临界应力；Ag为毛截面面积；Pr为二阶轴力承载力；Pc为有效轴力承载力；N为采用LRFD的轴压承载力要求(轴力设计值)；Mx，Mrx，Mry为采用LRFD的抗弯承载力要求(弯距设计值)；Mcx，Mcy为有效抗弯承载力。

中国规范GB 50017—2017，CECS 159—2004：

(19)

(20)

(21)

(22)

式中：Mx，My分别为X,Y向弯距设计值；γx，γy分别为X,Y向塑性发展系数；Wnx，Wny分别为X,Y向净截面模量；N为轴心压力设计值；A为毛截面面积；φ为稳定系数；αc为混凝土工作承担系数；Nu为毛截面轴压承载力；Nun为净截面轴压承载力；Munx，Muny分别为X,Y向净截面抗弯承载力；γ为安全及抗震调整系数。

6.2 中美规范构件内力对比

本工程主要构件有矩形钢管混凝土组合柱、箱形支撑和H形钢梁。

选取地上首层核心筒东南侧角柱，与其相连Y向支撑，地上10层南侧7.5m跨外框梁(上述三类各选取一根代表构件)，分别按美国规范ASCE/SEI 7-10与中国规范GB 50009—2012，GB 50011—2010计算出的单工况内力与组合内力设计值详见表14～16。(本节中的美国规范均指ASCE/SEI 7-10，中国规范均指GB 50009—2012，GB 50011—2010)。

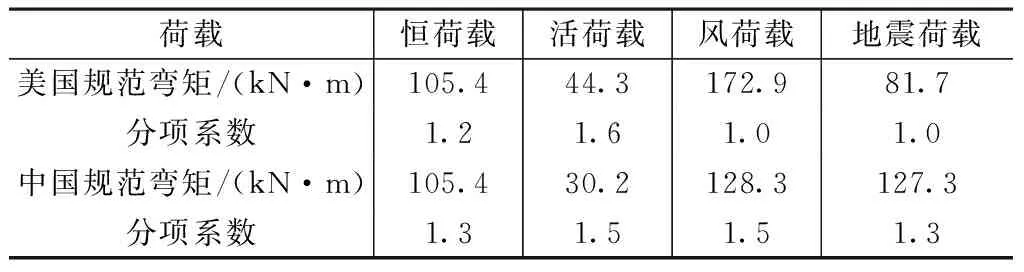
H形钢梁单工况内力 表14

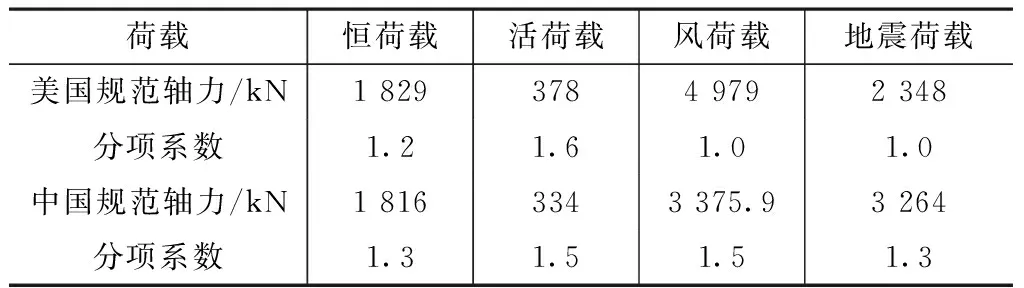
箱形支撑单工况内力 表15

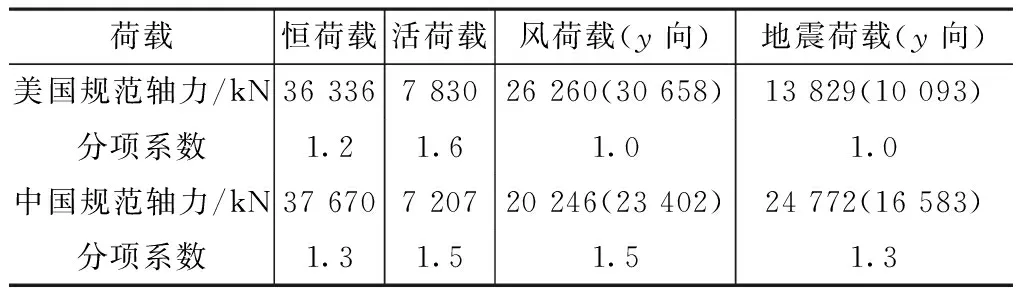
矩形钢管混凝土柱单工况轴力 表16

美国规范弯矩控制组合：

M=1.2×105.4+44.3+172.9=340.7kN·m

中国规范弯矩控制组合：

M=1.3×105.1+1.05×30.2+1.5×128.3

=360.8kN·m

中国规范组合大5.9%。

美国规范轴力控制组合：

N=1.2×1 829+378+4 979=7 551.8kN

中国规范轴力控制组合：

N=1.3×1 816+1.5×0.7×334+1.5×

3 375.9=7 775.4kN

中国规范组合大3.0%。

美国规范轴力控制组合：

N=1.2×36 336+7 830+30 658=82 091kN

中国规范控制组合：

N=1.3×37 670+1.5×0.7×7 207+1.5×

23 402=91 641kN

中国规范组合大11.6%。

经计算对比发现，美国规范规定的活荷载略大于中国规范。风荷载考虑分项系数后中国规范与美国规范相当，略大于美国规范。美国规范计算的地震力考虑反应谱修正系数R、冗余系数ρ或超强系数Ω0调整后，比中国规范计算的地震力更小。构件控制组合内力主要是风荷载工况为主，组合内力中国规范略大于美国规范。

6.3 主要构件应力对比

对6.2节选取钢梁、箱形支撑和矩形钢管混凝土柱，根据荷载控制组合分别采用美国规范ANSI/AISC 360-10与中国规范GB 50017—2017，CECS 159—2004计算出最大应力比，详见表17。

代表构件应力比 表17

6.4 构件对比情况

本次用于比较的两国规范模型截面大小一样，最终应力比两个模型计算结果比较接近，控制组合内力以风荷载工况内力为主(少部分有地震荷载工况)，相对中国规范模型梁的组合内力偏大5%～14%，应力比偏大8%～19%。支撑组合内力中国规范偏大2%～9%，应力比中国规范偏大3%～9%。柱组合内力中国规范偏大4%～15%，应力比中国规范偏大2%～22%。

由以上数据可以看出，内力的差别与应力差别并不完全一致。钢梁应力差别比内力差别更大，因同等条件下，美国规范梁的承载力比中国规范略高。支撑承载力两国规范非常接近，故内力差别与应力差别基本一致。组合柱美国规范抗力系数根据受力状态取值，受压取0.75、受弯取0.9；而中国规范抗力分项系数则是根据材料取值，混凝土1.4、钢结构1.125，故两国规范承载力计算也有不同。

7 结论

本文针对同一工程案例，按照中国及美国规范分别进行计算分析，同时对计算结果进行了对比，主要结论如下：

(1)本项目中，中美规范的整体指标和构件应力水平的计算结果均基本相当。

(2)结构的整体计算指标，包括层间位移角、二阶效应系数、刚度比等，中国规范的规定都比美国规范更严。

(3)就地震荷载而言，美国规范更注重延性设计，不同体系地震力相差很大；而中国规范地震力计算与体系基本无关。本项目按美国规范计算的地震内力远小于中国规范的计算结果。对于活荷载、风荷载，两国规范相差较小，活荷载美国规范的略大，风荷载则是中国规范的大2%～4%。对于构件的组合工况内力，中国规范相对美国规范大5%～15%。

(4)本项目中，美国规范纯弯构件(梁)承载力比中国规范略大；轴压构件(支撑)两国规范承载力基本一致；压弯组合构件(柱)承载力，两国规范因抗力系数有一定差异。本项目中国规范的构件应力比美国规范偏大2%～22%。因此，如按照美国规范进行设计，用钢量约减少8%，经济性更好。

(5)近几年，随着我国经济水平和技术的不断发展，规范安全度的要求也逐年提高。本项目如采用中国规范进行设计，其安全度略大于美国规范。