层叠式高层建筑多维风振效应试验研究

许 伟

(广东省建筑科学研究院集团股份有限公司， 广州 510500)

0 概述

风荷载是高层建筑结构设计的主控荷载之一，尤其在我国东南及华南等易受强台风影响的地区。对于规则的超高层建筑，由于结构高度越来越高，水平风荷载的控制效应愈发突显，从而影响结构基底倾覆力矩及剪力、层间位移角、顶部位移及加速度等关键抗风设计指标。由于建筑造型及使用功能的需求，部分建筑出现立面复杂、局部大悬挑等特殊外形，其平面、立面的不规则为结构设计带来了较大的挑战，尤其是对层叠式高层建筑而言，除了传统的水平及扭转风效应外，还须进一步考虑竖向风荷载的影响。

结构风致响应由平均风响应和脉动风响应组成[1]，为了方便设计师进行抗风设计，研究人员发展了一系列的等效静风荷载计算方法，如20世纪60年代由Davenport建立的“阵风荷载因子法”(GLF)[2]、20世纪90年代由Kasperski和Niemann提出的“荷载响应相关法”(LRC)[3]，以及20世纪90年代末周印等进一步提出的“基底弯矩阵风荷载因子法”(MGLF)[4]。工程上，预测结构风荷载的主要手段包括数值模拟[5-7]和风洞试验，其中高频天平测力试验和同步动态测压试验是较为常用的风洞试验方法[8-10]。

高频天平测力试验由于仅对模型底部的总体剪力和倾覆力矩进行测试，且在进行结构分析时，仅以考虑一阶线性模态为主，已不太适用于高度超过200m或者造型复杂的高层建筑[11]；而同步动态测压试验通过在刚性模型上布置足够多的测点，采用多点同步测压技术，同时对建筑物上的所有测点进行压力采集，可以得到详细的风荷载时空分布特性，在研究中被广泛应用，并且可考虑高阶模态影响[12-13]。

本文以某层叠式不规则高层结构为工程背景，进行刚性模型同步测压试验，分别采用覆面积分方法和三维有限元分析方法对结构的风荷载响应进行了全面深入分析。覆面积分方法给出了结构在各个风向角下基底等效最大倾覆力矩和扭转荷载，指导主体结构设计；三维有限元分析方法对悬挑部分竖向质量可能产生的动力效果进行了评价。

1 试验与分析概况

1.1 结构体系介绍

某工程主要建筑功能为会议室、展厅、观光平台等，包括地下2层，地上17层，建筑高度为153.6m，总共由9个方体建筑组成，33.6m以下由4个方体构成底座，平面尺寸分别为48m×48m和28.8m×28.8m，33.6m以上由1个33.6m，2个24m和2个19.2m的立方体交错叠合而成。结构体系采用斜交网格和劲性结构核心筒的双重抗侧力结构，上下方体间设置钢转换桁架，桁架最高3.8m，最长46.8m，跨度最大30.7m，斜交网格钢外框结构兼具结构受力和装饰作用。

1.2 风洞试验概况

刚性模型缩尺比为1∶200，分别在主体建筑的四周立面、悬挑方盒的顶面和底面区域布置代表性风压测点共780个。其中：立面上布置了10个测压区，对应的字母代码分别为A～H及S，T；同时在顶部方盒内表面也布置对应测压点，命名为DA，DC，DE和DG；在屋面及方盒悬挑部分的下表面布置10个测压区，字母代码分别为I～R；在底部4个方盒之间的通道侧面布置2个测压区，字母代码为U和V。限于篇幅，图1仅给出了主立面测点位置示意图。

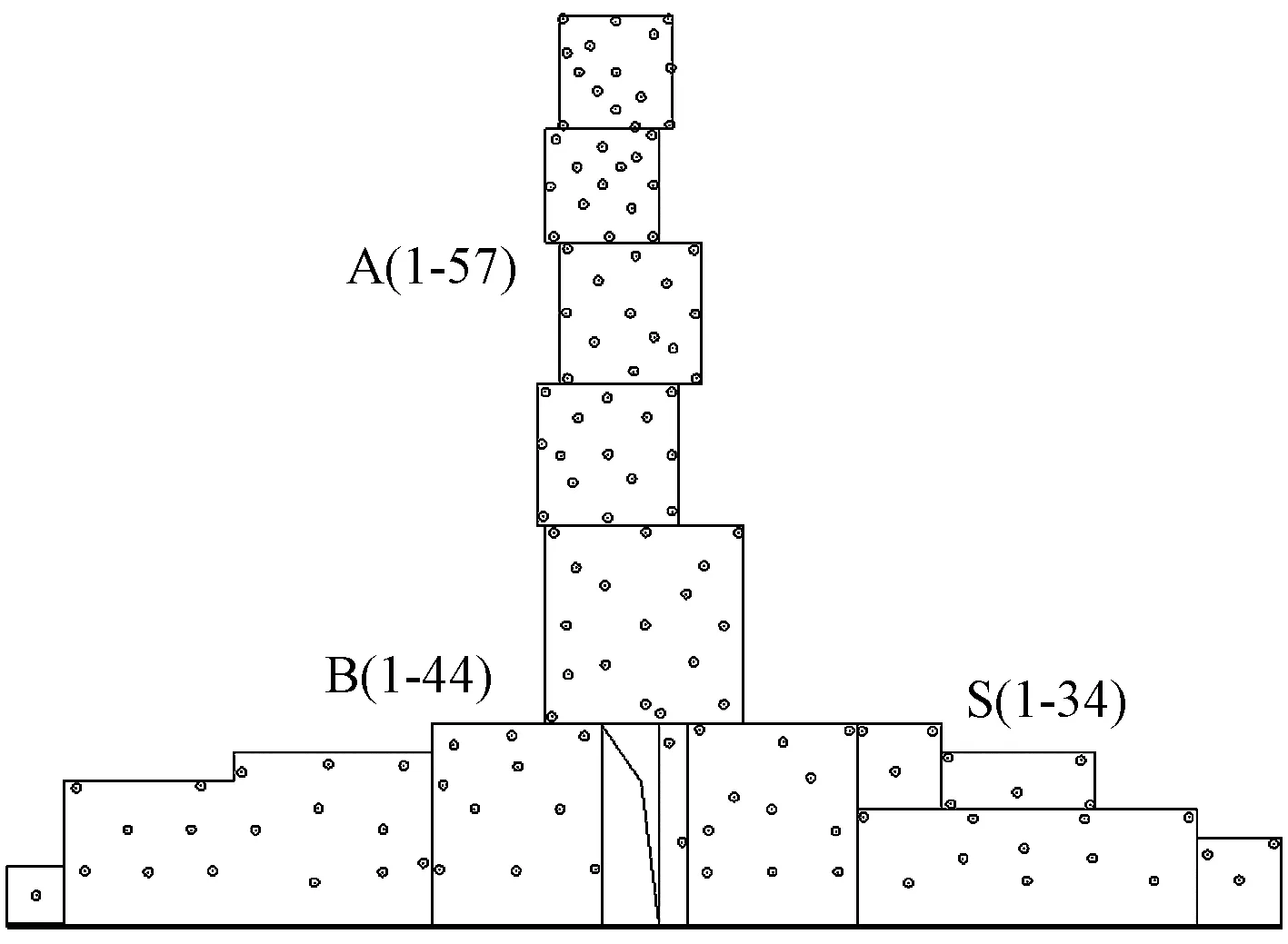
图1 主立面测点位置示意图

以主体建筑底部平面中心为圆心，详细模拟了周围一定范围内的周边建筑体块以考虑群体建筑的风干扰效应。试验时，从0°风向开始逆时针旋转，每10°一个风向角共进行36个风向下的风压测试。建筑刚性模型见图2，试验时定义的风向角见图3。

图2 刚性缩尺模型照片

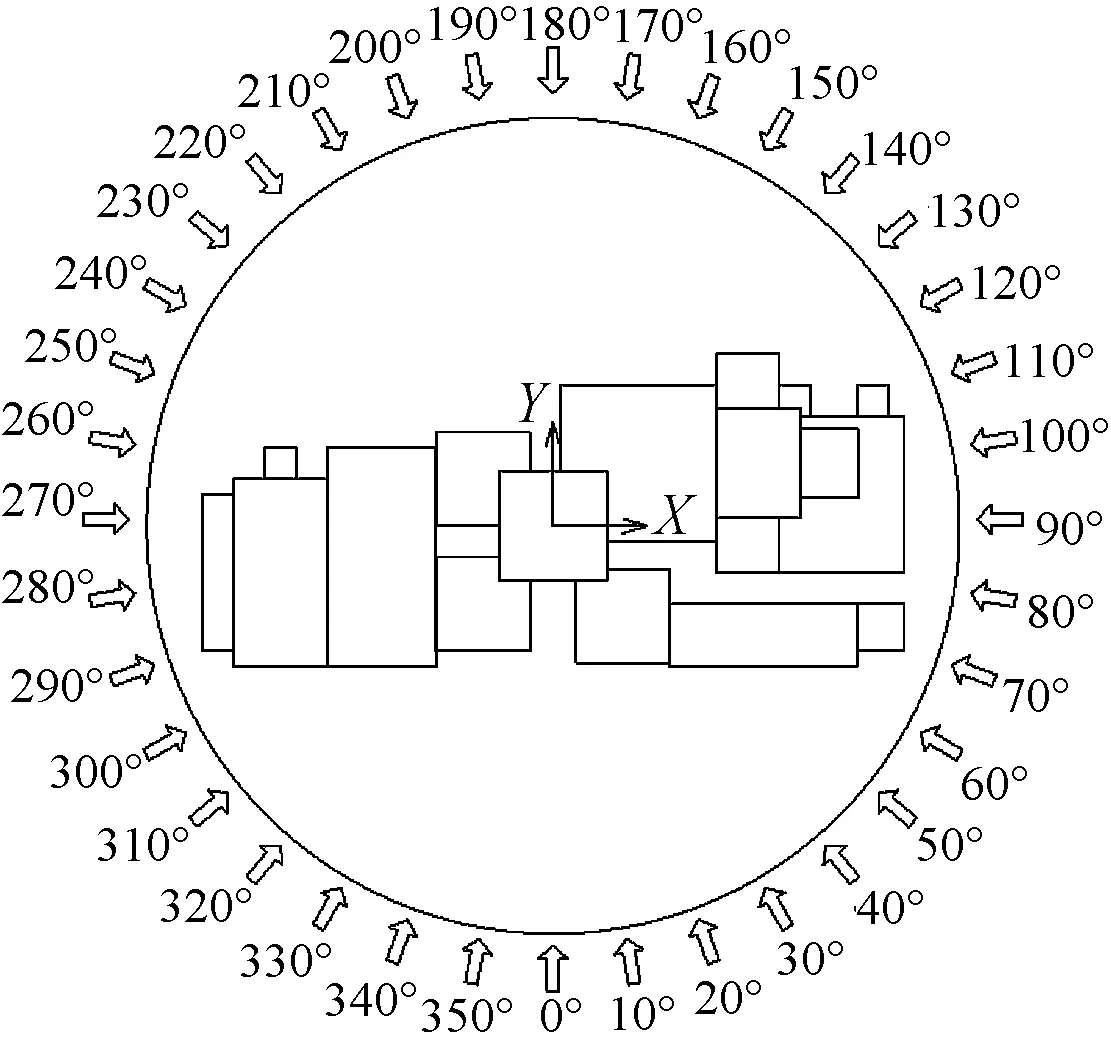
图3 风向角与结构坐标轴示意图

试验前根据建筑场地上游20km范围的地形、地貌和地面建筑物分布情况，采用ESDU数字风力模型对各个方位角上的平均风速剖面和湍流度剖面进行计算分析并进行分类。在风洞中采用尖塔、粗糙元和格栅的组合方式进行来流风场调试，详细的风剖面模拟结果见图4，图中风速比为任意高度处风速与参考点高度处风速的比值。

1.3 等效静风荷载分析方法

高层结构水平受力计算采用简化层模型，等效静风荷载计算需首先获得各结构层的风荷载激励时程。根据测压试验得到的建筑表皮各测点动态风压系数时程，结合各测点的控制面积、标高、平面坐标及测点风压对结构主轴(X，Y轴，见图3)的投影向量等参数信息，采用高频压力覆面积分方法计算得到各测点层风力系数时程，进一步通过样条曲线插值方法获得各结构楼层标高处的水平风荷载时程。除水平风荷载外，根据测点坐标可计算出各测点到结构刚度中心的距离，进而计算出相对刚心的扭矩时程。由于建筑外形为层叠式，不同方盒对应的楼层的风力系数插值采用分段取值的办法。

基于结构动力参数和积分得到动力风荷载时程，采用基于随机振动理论的频域方法进行结构风振响应计算。分析时，首先将得到的各楼层风荷载时程通过傅立叶变换求得其自功率荷载谱密度和互功率谱密度，作为结构风振响应计算的荷载输入项，此为非定常方法。非定常方法和拟定常方法相比，不但可以考虑来流的大气湍流特性，还能考虑风吹到结构表面而产生的结构特征湍流特性，且还能考虑周围环境对建筑结构的干扰作用，因而更为精确，尤其是当发生横风向的涡激振动响应时，必须采用非定常的方法来计算。

等效静风荷载计算采用改进的荷载响应相关法(LRC)，并考虑多阶惯性力进行组合，总共采用了25阶振型进行组合计算，其中结构前5阶自振频率分别为0.353，0.413，1.209，1.389Hz和1.538Hz。结构计算时，脉动风荷载的峰值因子取为3.5，主体结构为钢结构，故阻尼比取为0.01。

1.4 竖向振动三维有限元计算

本建筑平面基本为矩形，但从上到下分布不规则，有部分盒体悬挑出来。结构体型较为复杂，需要运用三维有限元模型分析悬挑部分竖向质量可能产生的动力效果，荷载激励包括悬挑部分上下表面的竖向风荷载和立面上受到的水平风荷载。同时采用三维分析中结构在水平方向风荷载作用下的基底反力及典型层加速度来校核简化模型的计算结果。

为了研究悬挑部分盒体的竖向受力情况，采用三维有限元分析方法建立该结构有限元模型，着重分析大悬挑结构上下表面同步风压作用下的动态响应，分析其动力作用效应。有限元模型采用了梁单元Beam44、壳单元Shell43和质量单元Mass21。根据结构模型的几何信息、材料信息和截面信息建立精细有限元模型，共划分梁单元6 008个，质量单元3 047个，壳单元1 214个，节点3 103个，计算时采用瑞利阻尼，有限元模型如图5所示。

图5 结构分析模型示意图

根据风洞试验脉动风压测量采样频率为313Hz，取采样时间间隔约0.003 195s，根据计算的试验时间比，实际采样时间间隔为0.125 8s，取每个测点数据形成3 000个时程步进行计算。

2 水平风振效应分析

2.1 结构顶部风振加速度响应

由于高层建筑阻尼比较小，尤其对于不规则的超高层建筑，动力风荷载产生的舒适度问题往往成为控制因素。由于结构位于众多建筑物当中，周围建筑物的干扰作用明显，因此对于大多数的风向角，较难区分来流的顺风向与横风向。因此本文并不按照顺风向和横风向来区分结构的振动形式，而是主要给出了结构X，Y向的风振加速度响应结果。

图6(a)和图6(b)分别给出了在10年重现期风压0.30kN/m2下结构顶部使用楼层(楼板标高H=122.4m)处X向和Y向加速度响应峰值随风向角变化的情况。从图中可以看出，各风向角下X，Y向加速度波动范围相对较小，无明显的横风向风振效应，这与本工程所处的周围建筑环境、建筑体型有着直接关系。一般而言，复杂的周边环境、凹凸错落的建筑外形有助于扰乱流动分离的一致性，并更多地表现为局部特征湍流，从而有助于降低结构的横风向风振效应。

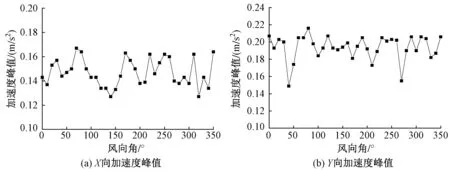
图6 结构顶部使用楼层加速度峰值随风向角变化

同时本文对建筑物顶部的X向加速度、Y向加速度进行合成处理。当用建筑物顶部X向和Y向最大加速度响应叠加为建筑物中心最大加速度时，需乘以折减系数0.8，即：

(1)

式中ax，ay和a分别为结构顶层的X向加速度峰值、Y向加速度峰值和合加速度峰值。

表1列出了各风向角下结构顶部使用楼层(H=122.4m)处的合加速度峰值，其中80°风向角下合加速度最大，为0.217m/s2，满足《高层建筑混凝土结构技术规程》(JGJ 3—2010)中关于公共建筑的人体舒适度要求。

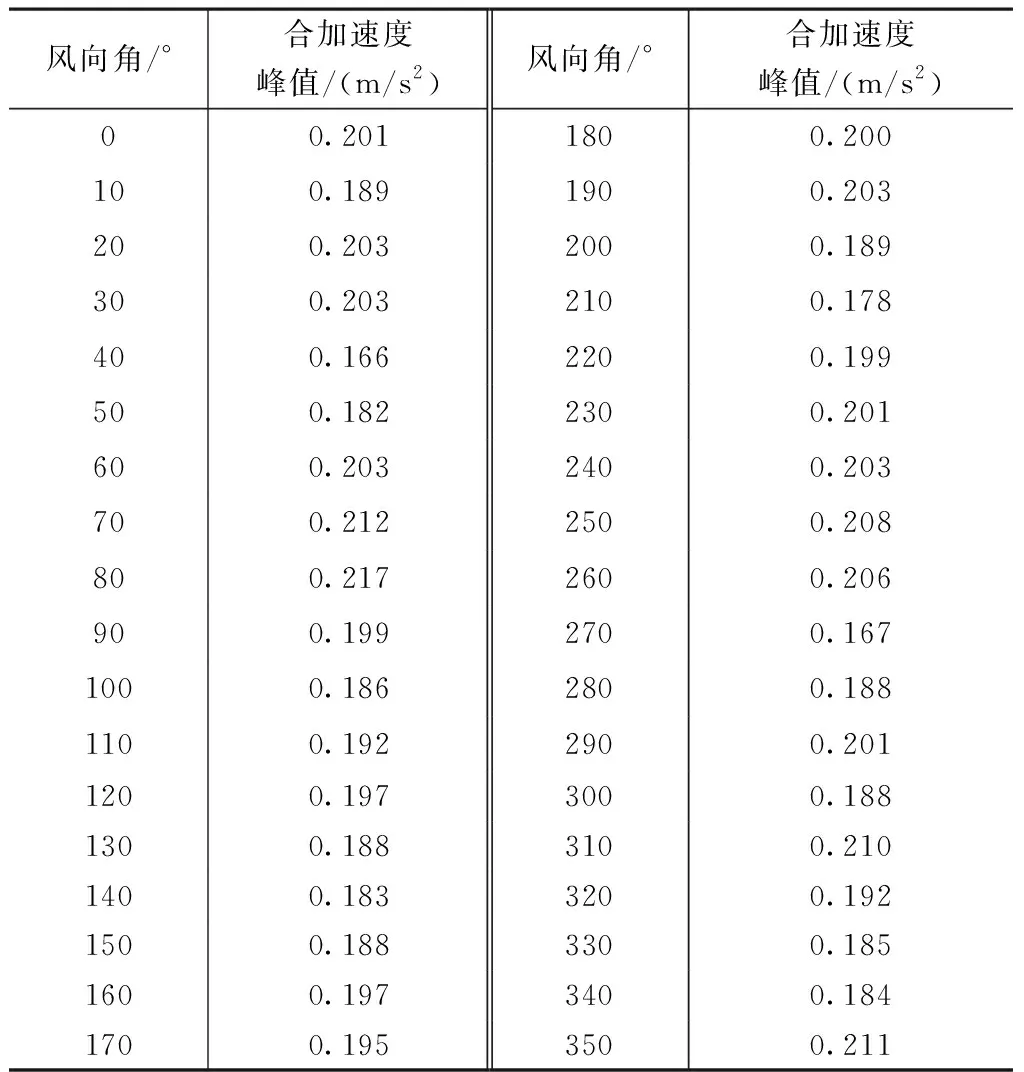
结构顶部使用楼层合加速度峰值 表1

2.2 等效静风荷载分析

风荷载作用下结构底部等效倾覆力矩能表征大楼的整体风力，同时通过比较各风向角下倾覆力矩的平均分量、背景分量和共振分量组成，可以分析结构是否存在典型的横风向振动问题。图7给出了基本风压为0.60kN/m2时，绕X轴和Y轴等效基底倾覆力矩随风向角变化曲线。由图7可知，绕Y轴等效基底倾覆力矩在80°和250°风向角附近最大，绕X轴基底倾覆力矩在0°和180°风向角附近最大，且随风向角变化较显著。从出现较大基底倾覆力矩的风向角来看，结构主要受顺风向荷载控制。将各风向角下结构的基底倾覆力矩的三分量进行详细分析，分别研究各分量之间的相对大小，图8给出了6个典型风向角下基底倾覆力矩平均分量、背景分量和共振分量的簇状柱形图，其中除了上文中提到的4个不利风向角外，同时也加入了90°及270°两个正交风向角。从图8中可以看出，各风向角下背景分量在总力矩所占比重起伏较小，主要在20%～40%之间，且共振分量与背景分量随风向角的变化规律一致，平均分量与背景分量占比呈负相关特性。当基底倾覆力矩处于低位时，平均分量所占比例较小，共振分量作用明显，但总体倾覆力矩并不起控制作用，表明本层叠式高层建筑在风荷载作用下的横风向振动不明显，基底倾覆力矩由顺风向控制。

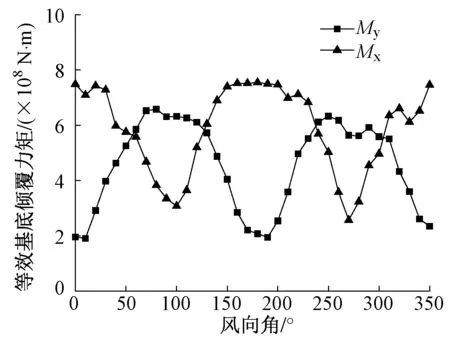
图7 等效基底倾覆力矩随风向角变化图

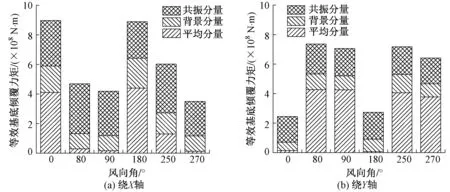
图8 等效基底倾覆力矩分量随风向角变化图

作用在结构每层上的扭矩根据其产生原理，主要包括三个组成部分：首先是平均风荷载作用偏心引起的扭矩；其次是结构风致扭转振动引起的扭矩；最后是结构质量中心和刚度中心不重合产生的扭矩。将上述三个部分的扭矩按照矢量叠加，就可得到作用到结构每层上的总扭矩。图9为基本风压为0.60kN/m2时，等效基底扭矩随风向角变化曲线，最大值发生在310°风向角下；同时等效基底扭矩随风向角变化比较显著，当风从斜角吹来时，基底扭矩较大，结构设计时扭转风荷载不可忽略。

图9 绕Z轴等效基底扭矩随风向角变化图

3 竖向风振效应分析

3.1 竖向位移分析

结构仅在自重作用下的竖向位移最大值为7.7cm，出现在顶部盒子的悬挑部位，图10为悬挑部位各节点竖向位移统计图，大部分悬挑节点竖向位移在3～7cm之间。相比之下，结构悬挑部分在竖向静风荷载作用下的竖向位移则相对较小，最大位移仅为0.17cm，为重力作用下最大竖向位移的2.2%。

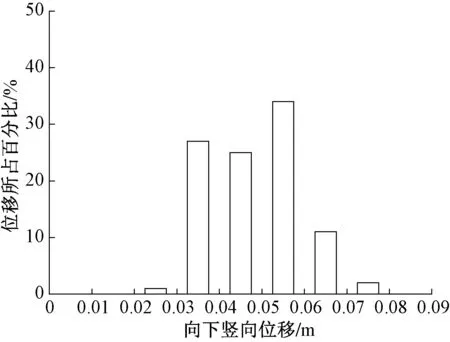
图10 自重作用下悬挑部分结点位移统计

在竖向动力风荷载作用下悬挑部分的竖向位移也为毫米级，最大动力位移为重力荷载作用下位移的5%左右。图11为0°，70°，130°风向角下结构悬挑部位最大竖向位移的节点位移时程。从上述计算结果可知，悬挑竖向位移由恒荷载控制，风荷载影响较小。说明悬挑部分在风荷载作用下很难出现类似整体结构的风振效应，可将悬挑部位在风荷载作用下的竖向振动视为刚性体的阵风效应。

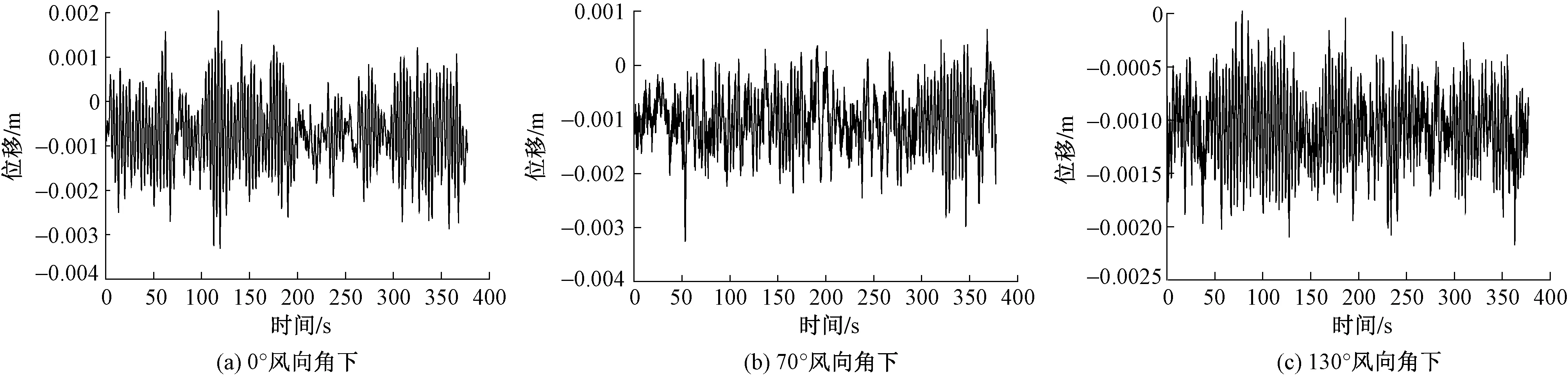
图11 风荷载作用下悬挑部位竖向位移最大处节点位移时程曲线

3.2 悬挑部分竖向等效静风荷载

多项国际规范推荐：当结构基阶频率大于1Hz，仅考虑伪静力计算结果精度足够。结构的最大悬挑长度为9.6m，选取最不利悬臂部分，将悬挑部分在悬挑端部堪固进行模态分析，一阶模态频率为4.78Hz，远大于国际规范中关于风敏感结构1.0Hz的规定限值，因此可近似忽略悬挑部分在脉动作用下自身的动力响应。

(2)

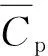
对于各分区，可根据式(2)分别得到正、负两个风压峰值，由于悬挑结构上、下表面可能出现的不利风压叠加情况，因此对各风向角下、各分区风荷载值进行统计时，需分别考虑向下等效静风荷载和向上等效静风荷载两种情况。

4 结论

(1)对于不规则建筑，需同时考虑风致平动和扭转振动效应，尤其是质量、刚度中心不重合时，扭转效应不可忽略。

(2)不同风向角下基底倾覆力矩中背景分量所占比重起伏较小，平均与背景分量占比呈负相关特性；共振分量作用明显时，总体倾覆力矩较小，表明本层叠式高层建筑在风荷载作用下的横风向振动效应不明显，基底倾覆力矩由顺风向控制。

(3)大悬挑部分相对主体结构较刚，其在风荷载作用下的竖向振动可按刚性体的阵风效应考虑。

(4)采用覆面积分方法分析层叠式高层建筑风致振动效应的方法是可行的，可为类似项目的风振效应分析提供参考。