基于金属材料强度及储能密度的储能飞轮结构设计

赵宇兰，白金刚，赵 雷

（1.清华大学核能与新能源技术研究院，北京100084；2.哈尔滨电气股份有限公司中央研究院，哈尔滨150028）

0 前言

储能飞轮是一种将能量或动量储存在高速旋转轮体中的装置，利用现代电力电子技术，将电力系统中的电能转换成飞轮的旋转动能，待需要时再将飞轮旋转动能转换成电能，供负载使用。随着高强度复合材料、磁轴承、高速电机／发电机及大功率高速电力电子等技术的飞速发展，以及清洁能源、能源高效利用的迫切需要，储能飞轮的一些技术特征又重新引起了人们的关注与审视［1，2］，因此，提出 “现代飞轮”及“飞轮电池”的概念［3］。不同于传统飞轮，虽然现代飞轮同样是以机械方式存储及释放电能，但其转速更高、功率更大、体积重量更小。在诸多的储能方式中，如：电化学电池、超级电容、超导储能等，飞轮电池具有许多独特的性能［4，5］：

（1）纯机械－电能互相转换过程，无派生环境问题；

（2）充放电循环次数与寿命无关，只与机械自身寿命有关；

（3）放电深度与寿命无关，仅取决于负载电压适应能力与电力控制技术；

（4）可根据实际需要设计单机大功率或超大功率 （MW、GW级）、快速 （ms、μs级）的充放电系统，不影响使用寿命，且相对的总体体积重量较小，更适合于高速充放电场合；

（5）可实时直接观测充放电及存储状态，转子转速直接表征充放电或存储状态，即使处于大型阵列中，各单元电力状态也可被直观地实时监测，无需增加额外设备；

（6）运行环境因素 （湿度、温度等）对存储状态无影响与限制；

（7）充电保持时间相对较短，更适于短期多次、大功率等应用，如地铁、电网电力快速调峰等。

储能飞轮工作模式包括充电、放电以及能量保持阶段。充电时，电动机带动飞轮，将电能转化为机械能存储在高速旋转的飞轮中；放电时，飞轮带动发电机发电，此时机械能转变为电能，并通过电力电子设备输出；能量保持阶段时，储能飞轮保持额定转速运行［6］。

储能飞轮的结构不同于高速电机、高速涡轮转子等高速转子［7］，也不同于以角动量为主要指标的航天飞轮结构［8］。由于设计目标的多样性，储能飞轮在结构上几乎没有固定的模式，有多种选择形式。

一般地，对于飞轮电池而言，总体的设计目标是在已有的材料强度极限范围内，最大限度地提高储能密度及储能量，或者最大限度提高充放电功率。为实现这样的目标，涉及的关键因素很多，其中，与飞轮转子结构有关的主要有材料与对应的结构形状选择、陀螺力学特性、转速选择与支承选型、高速电机／发电机结构选择等等［9］。

文献 ［10］针对高储能密度飞轮的工程设计提出了优化流程，其试验飞轮转子采用高强度铝合金芯轴、薄壳及环壳组合轮毂和纤维复合材料轮缘组合结构，试验飞轮外缘线速度达到660m／s。文献 ［11］基于不同的应用要求，对圆柱复合材料飞轮转子进行了结构设计流程优化。文献 ［12］针对航空应用场合下的复合材料转子储能飞轮进行了结构以及控制算法的优化。文献 ［13］推导了复合材料储能飞轮在高速旋转过程中径向应力和环向应力的表达式，分别研究了单层飞轮以及多层飞轮，分析了应力影响因素。文献 ［14］分析多种结构优化方法，优化了铝合金轮毂飞轮外轮廓体积最大值及轮毂各部分的尺寸。文献［15］对600W·h飞轮储能试验样机伞状结构铝合金飞轮进行了结构优化，采用最优控制原理建立飞轮优化设计的数学模型，然后根据飞轮的设计要求得出优化后的飞轮基本结构和基本尺寸，并对优化后的飞轮储能密度进行分析。文献 ［16］推导单层轮缘以及多层轮缘过盈装配后的结构应力和应变方程，并通过仿真模拟，建立碳纤维复合材料的微观模型，通过同步建模，构建出形状最优的飞轮轮毂。文献 ［17］设计了新型双层飞轮转子结构，使转子在充放电时的轴向力相互抵消，有效地提高了转子稳定性。文献 ［18］针对配备高速表贴式永磁电机的飞轮储能系统进行了转子力学特性研究，得到转子优化方案。

金属材料相对于纤维增强型复合材料虽然极限强度略低，但由于质量密度大，同样体积的飞轮也可以获得较大的储能量；另外，由于金属材料各种性能的各向同性较好，设计制造工艺简单，质量更容易保证，能保证飞轮具有更长的使用寿命，因此，在储能飞轮领域，选择金属材料仍然具有重要的使用价值与现实意义。

1 飞轮储能量与储能密度

单个飞轮系统所能提供的最大功率P、总储能量E以及充放电最短时间Δt三者存在如下关系：

其中，功率P的范围主要取决于负载需求及电机／发电机的设计功率，可以根据实际需要选择；Δt则取决于总能量E在额定功率Pn条件下的持续时间与放电深度η%。为保持输出电压的稳定可用，放电深度一般为75% （降速至1／2）至90% （降速至1／3）。如能发展更好的电力控制技术，可进一步加大放电深度。

根据储能量要求，考虑放电深度与充放电功率，暂忽略机械效率，飞轮的总机械能 （即储能量）为：

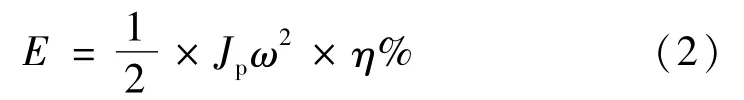
其中，Jp为沿旋转轴飞轮转子的极转动惯量，kg·m2；ω为转子角速度，rad／s。为获得更多的储能量，主要的设计目标有：提高转子角速度和极转动惯量，并尽量降低体积重量。

飞轮的比能量 （即储能密度）有：单位质量所储存的能量，称为质量储能密度或质量比能量，通用单位为W·h／kg；单位体积所储存的能量，称为体积储能密度或体积比能量，通用单位为W·h／m3。通常比能量都选择质量比能量，或称储能密度。根据式（2）（暂不计放电深度η%），飞轮的比能量 （或储能密度）可以表示为：

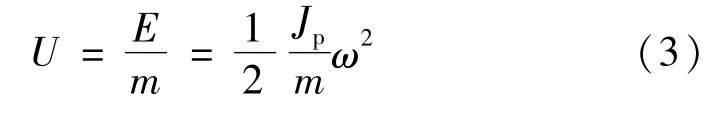
其中，Jp／m为单位质量转动惯量，与储能密度U成正比，是结构优化的重要内容，比如，扁平转子比同样质量的细长转子的单位质量转动惯量大；进一步，飞轮储能密度U还与角速度平方成正比。转速（或角速度ω）则受限于结构材料的极限抗拉强度，而不同结构形状，所能达到的极限转速不同。因此，结构的设计优化需要同时对转速和材料极限强度进行综合考虑。

因此，在结构方面的设计优化目标实际上变成如何在最小的体积重量条件下获得最大的转动惯量，同时获得更高的极限转速。因此，需要对储能飞轮的结构参数指标及相关因素进行详细的分析论证，主要内容有：

（1）材料的选择，依据不同的材料特性，选出适合于飞轮应用的转子材料；

（2）对典型轮体形状进行强度计算和分析；

（3）给出飞轮可选用材料及优化的转子形状结果，并依据比能量、能量、重量、转速等指标，进行转子尺寸的论证分析；

（4）针对考虑效率指标、满足重量体积等指标进行的论证分析。

2 材料强度与形状系数定义

圆形旋转结构中的微元的强度有如下规律［19］：

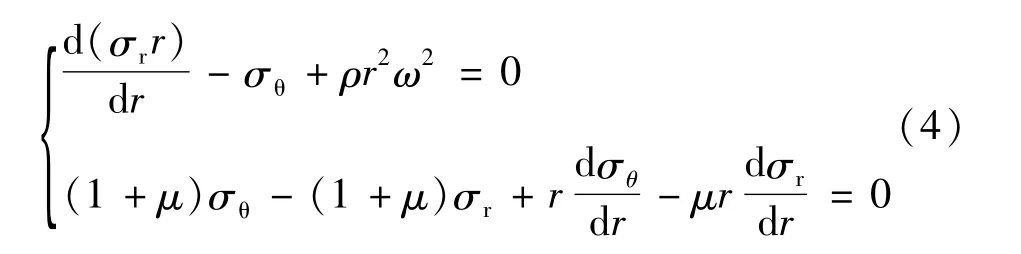
其中，σr为径向强度，MPa；σθ为切向强度，MPa；r为半径，mm；ρ为材料密度，kg／m3；ω为角速度，rad／s；μ为泊松比。求解式 （4）可得：

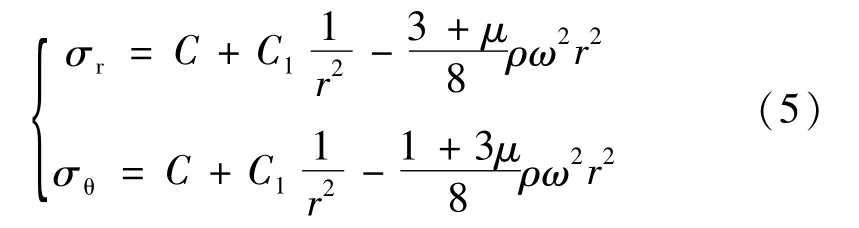
式中，C、C1为积分常数，具体数值由受力边界条件决定。当形状结构确定，C、C1为定值。针对选定的形状，可求得该条件下的σr及σθ。

对于不同结构，角速度的平方与飞轮材料强度的具体表达式不同，但两种成正比例关系［19］，如下所示。

式中，σ代表广义强度；C0为与结构边界条件有关的比例系数。由式 （6）可得：

将式 （7）代入式 （3），并用σmax代替σ，可得：

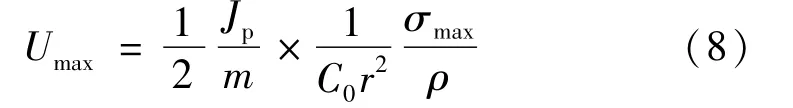
式中的极转动惯量Jp、质量m、半径r及比例系数C0，都与结构形状有关，当飞轮结构确定后，均为定值。因此，综合各个参数，可以定义飞轮形状系数Ks如下：

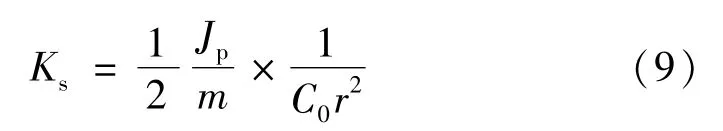
该系数由在一定转速限定下的结构形状确定，可以根据选定结构推导其具体表达式。综合形状系数Ks及比强度σmax／ρ，进一步由式 （8）得到比能量U的最大值Umax为：

式中，ρ为飞轮材料密度；σmax为转子实际承受的最大应力。考虑实际材料强度许用系数Km，根据式（10），飞轮的比能量极限 （最大储能密度）Umax可写为：

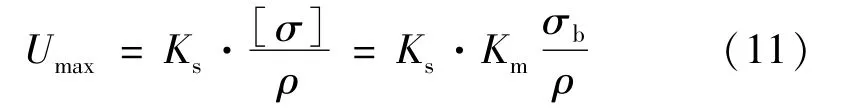
式中，σb为飞轮材料强度极限；Km一般取0.6～0.8。由此可见，比能量极限Umax正比于材料的比强度［σ］／ρ和飞轮形状系数Ks。要得到高比能量，必须选取比强度高的材料。高强度材料大体可以分为两类：一类为金属合金，如高强度合金钢、高强度铝合金、钛合金等；另一类则是各种增强复合材料，如碳纤维、玻璃纤维等［20］。

在选择高强度材料的基础上，合理选择飞轮的结构形状系数Ks，可以有效提高飞轮的比能量极限，从而实现飞轮转子整体结构的优化。

3 各类型形状系数K s分析

3.1 中心无孔实心圆盘的K s

如图1所示，中心无孔实心圆盘结构，r为圆盘上任意点半径，re为圆盘最大半径。为简化分析过程，未考虑支承及电机结构部件。

图1 中心无孔实心圆盘

边界条件：C1＝0；r＝re时，σr＝0，代入 （5）得解为：

式中，α＝r／re。对于中心无孔圆盘，即r＝0时，σr与σθ相等，并同时达到最大值，则：

中心无孔圆板的质量和极转动惯量分别表示为：

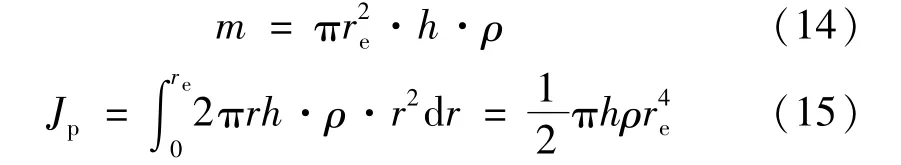
将式 （14）、式 （15）代入式 （3），有：

将应力极值表达式 （13）代入式 （16），得：

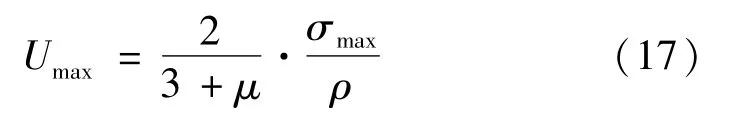
对比公式 （10），可知 Ks＝2／（3＋μ），对于金属材料，其泊松比一般在0.3左右，因此，中心无孔圆盘的结构形状系数Ks＝0.61。

3.2 中心有孔圆盘的K s

如图2所示，中心有孔圆盘结构，为简化分析过程，同样未考虑支承及电机结构部件。图中ri为圆盘内径，re为圆盘外径。

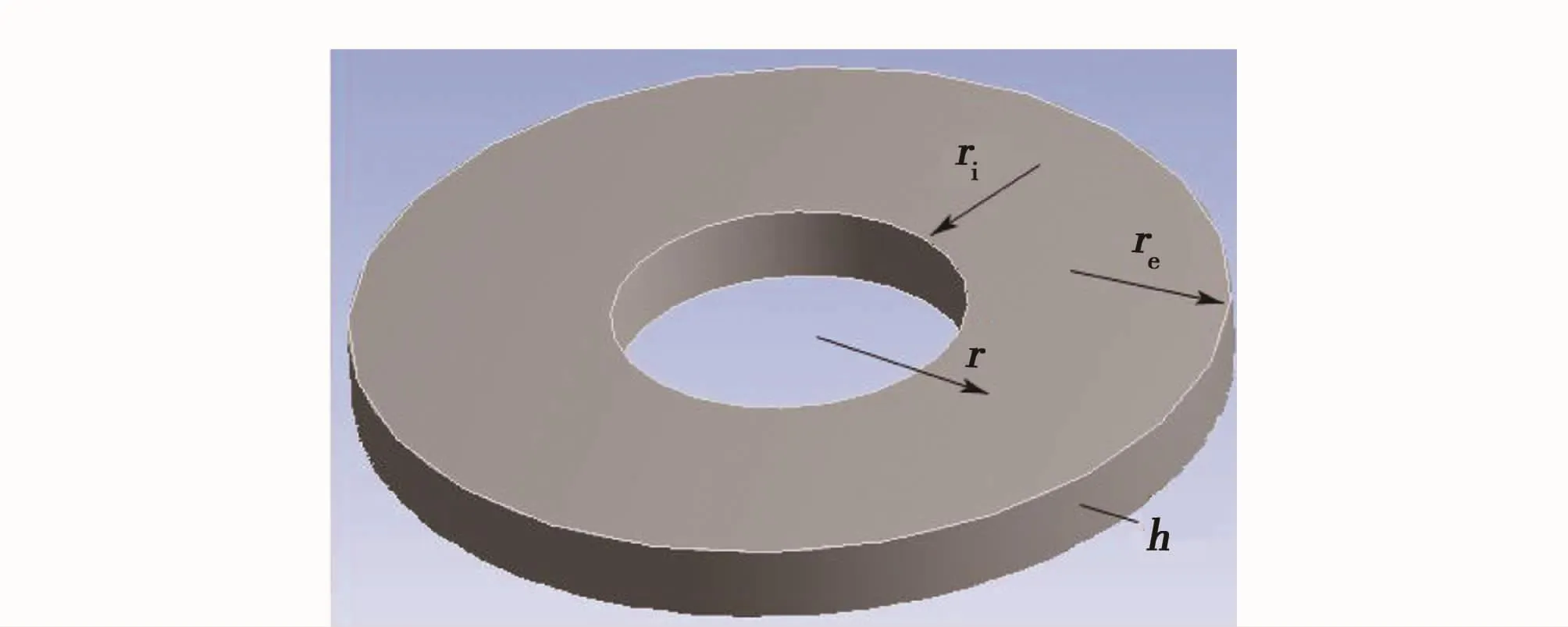
图2 中心有孔圆盘

边界条件：r＝ri，σr＝0；r＝re，σe＝0，得解为：

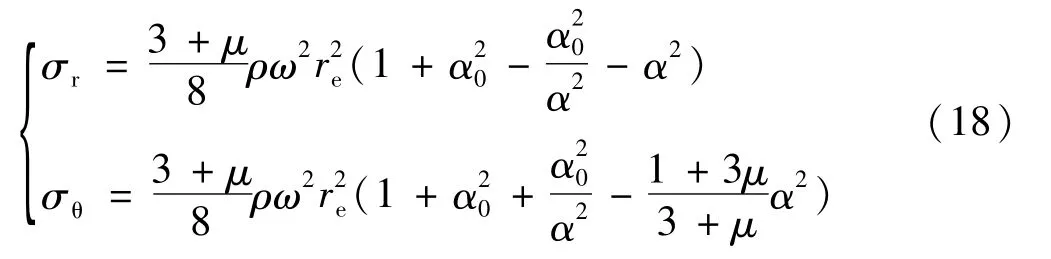
其中，α0＝ri／re，α＝r／re。当 r＝ri时，σθ达到最大值：

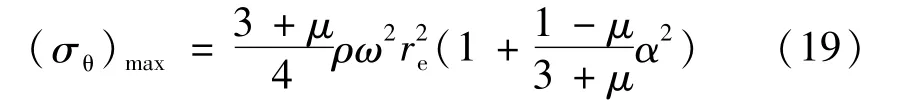
类似式 （14）、（15），求取中心有孔圆盘的质量m、极转动惯量Jp，代入式 （11）可得：

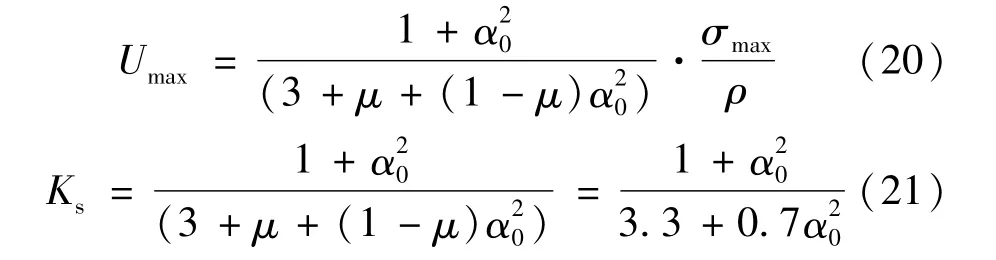
选取几个有代表性的半径比α0，计算对应的形状系数，见表1。

表1 中心有孔圆盘的K s

用曲线表示不同内外半径比、线速度与储能密度的相互关系，如图3所示。

图3 中心有孔圆盘边缘线速度与储能密度曲线

在相同的外缘线速度条件下，内外径比大，获得的储能密度略高。为获得较大的比能量，内外径比应适当选取较大值。

显然，中心有孔圆盘结构的内孔越大，构成的飞轮其形状系数越大。选择不同金属材料对应的强度值，计算可能达到的比能量值，见表2。

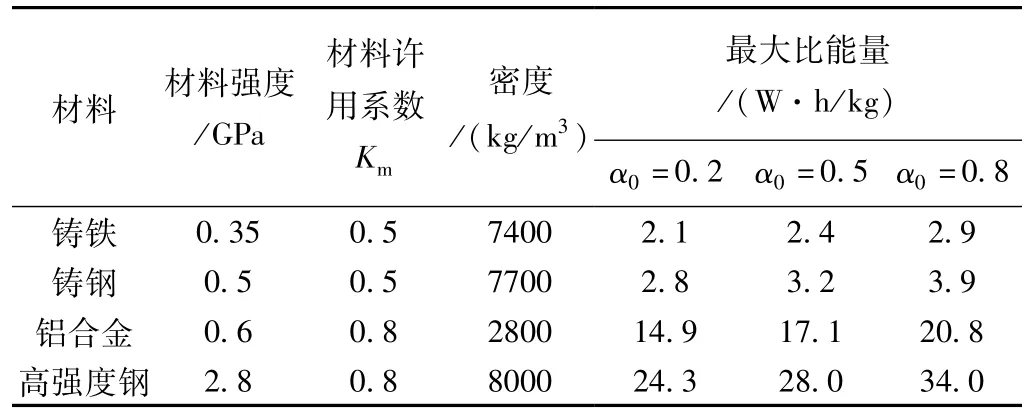
表2 金属材料中心有孔圆盘比能量极值

3.3 薄壁圆筒的K s

薄壁圆筒形转子结构如图4所示。通常，配套电机与支承或置于圆筒内部，或者通过轮毂与其相连接。这种结构也是许多复合材料飞轮的结构选择形式之一。

图4 薄壁圆筒外形图

对于薄壁圆筒结构，有：r≈ri≈re≈R，其中R为薄壁圆筒半径，代入式 （5），得：

同样，参照式 （14）、（15），求取薄壁圆筒的质量m、极转动惯量Jp，代入式 （3）可得：

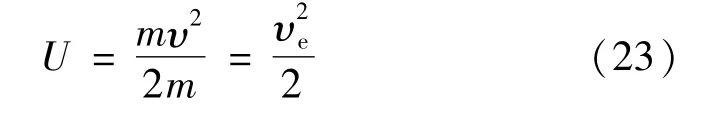
其中，ve为飞轮外缘线速度。薄壁圆筒形转子的储能密度与外缘线速度的平方成正比，综合上式与式（10），可以得到：

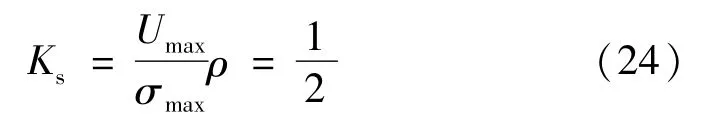
选取不同金属材料，计算可能得到的薄壁圆筒形转子的比能量，见表3。

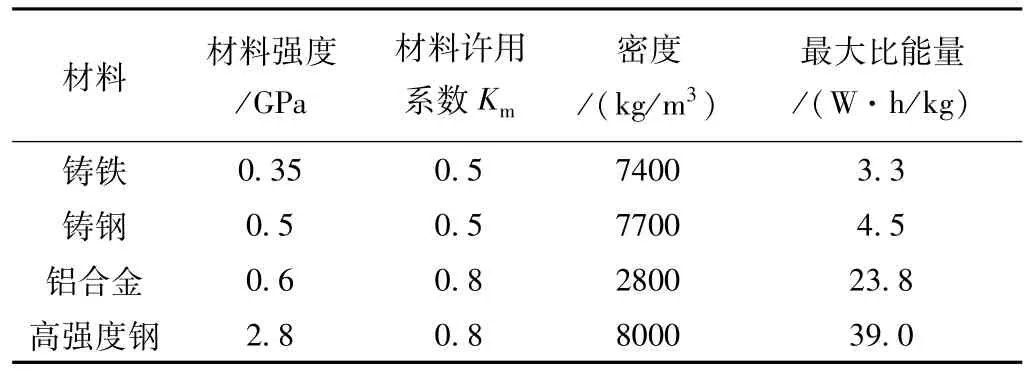
表3 薄壁圆筒形转子的比能量

3.4 等应力圆盘的K s

等应力圆盘即在圆盘上各点均存在σr＝σθ，盘的厚度h不再为常数，而是半径r的函数，h＝f（r）。微元的力平衡方程如下：

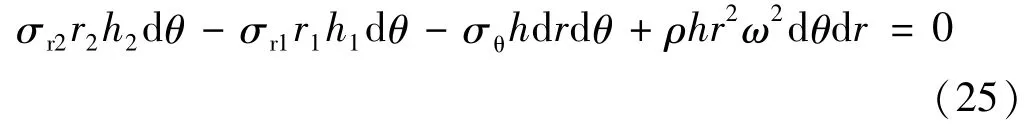
其中，角标1、2分别代表任意两点。将σr＝σθ代入上式，进一步简化可得：

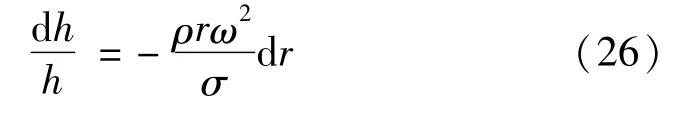
积分得：

其中，h0为圆盘高度。

等应力圆盘结构如图5所示。

图5 等应力圆盘外形图

等应力圆盘的质量和极转动惯量分别表示为：

对比上式与式 （10）可见，等应力圆盘的飞轮形状系数Ks＝1。

3.5 其他形状的K s

除了上面的四种形状，常见的还有近似等应力圆盘、圆锥截面圆盘以及棒状圆柱形等。

针对各种不同形状的金属材料，取泊松比μ＝0.3，假定圆盘不受径向表面力的作用，计算各种形状的飞轮转子对应的形状系数Ks以及不同材料对应的比能量最大值Umax，具体结果见表4。

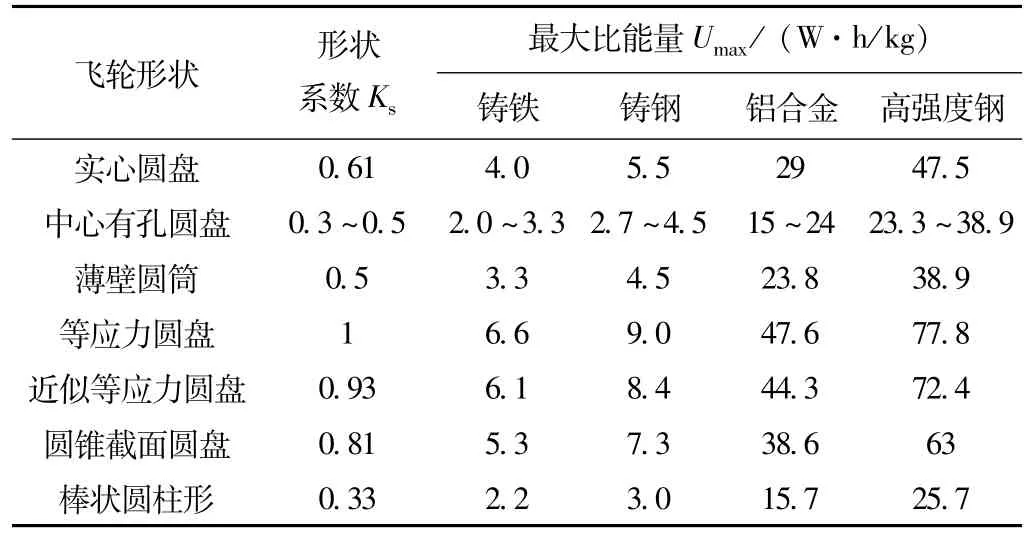
表4 不同飞轮的形状系数及比能量

4 飞轮转子选型强度分析对比

现针对高强度合金钢转子进行结构优化。提出一种近似等应力转子结构，飞轮主体为具有斜面的阶梯变截面结构，所述斜面的阶梯变截面结构为沿飞轮水平中心向上和向下直径逐渐缩小的阶梯结构，且阶梯间采用斜面过渡。

图6和7分别所示为在同等最大直径为500mm的设计条件下，圆柱形飞轮转子与新型近似等应力转子的结构示意图。当转子转速为15000r／min时，两种飞轮转子的应力分布情况如图8与图9所示。

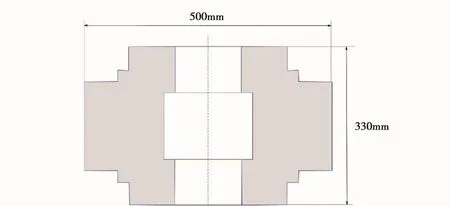
图6 圆柱形飞轮转子示意图

图7 近似等应力分布转子示意图

图8 圆柱转子应力分布

图9 近似等应力转子应力分布

通过应力分布对比结果可知，大储能量变截面转子由于具有近似等应力圆盘的结构设计，具有较好的应力分布，其应力峰值较圆柱转子有显著减少。

近似等应力分布转子飞轮的结构参数见表5。

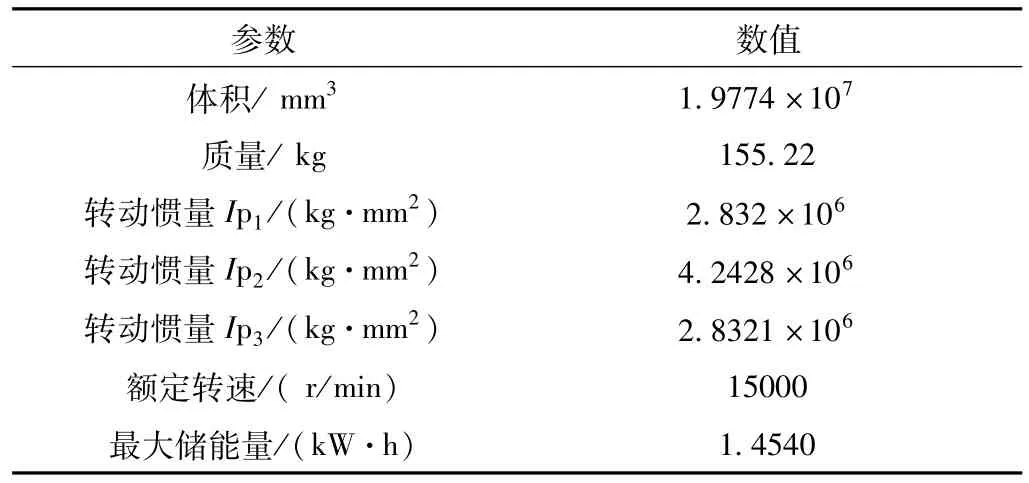
表5 飞轮旋转主体物理参数

在转子形状方面，对于金属材料，采用等应力盘是最优的，但是等应力和圆锥截面圆盘由于加工困难，在工程上采用较少。实心圆盘加工方便，形状系数也比较大，为常用转子形状。鉴于等应力转子加工难度较大，推荐选用金属近似等应力分布转子，形状系数较大，结构优化合理。

5 结论

对于金属材料飞轮的设计，总体原则是在已有的材料强度极限范围内，最大限度地提高储能密度及储能量，或者最大限度提高充放电功率。通过分析及推导，本文主要得出了以下结论：

（1）金属材料虽然相对于纤维增强复合材料的极限强度较低，但是，结构设计与制造工艺简单，使用寿命更容易保证。对于一些不追求高储能密度的应用，仍然是一种较好的解决方案。

（2）转速是获得高储能密度的关键指标，选择金属材料设计飞轮，高强度材料是提高储能密度的基础；同时，可以选择设计形状比较复杂的结构以适应需求。这种设计分析方法适用于各向同性的金属材料，对于各向异性的复合材料不适用，但是基本的计算方法类似。

（3）相同的金属材料，可以供选择的形状有多种，不同形状的形状系数不同，实心圆盘加工方便，形状系数也比较大，所以是目前金属材料飞轮的较普遍形状；等应力圆盘、近似等应力圆盘及圆锥截面圆盘虽有一定的加工难度，但是形状系数较高。为获得更高的储能密度，需要在选择尽量高的形状系数与较低加工制造难度之间合理优化。

（4）在具体设计优化过程中，还需要兼顾电机／发电机以及支承部件的结构形式，以期在有限强度的前提下获得最大的储能密度。