浅析新课改下高中数学基本不等式解题技巧

陈大祥

(江苏省扬州市宝应县画川高级中学 225800)

新课改下，基本不等式不仅是高中数学具体教学的重点，而且还是高考命题人重点关注的内容.通常而言，基本不等式有多种类型，学生在具体解答的时候，就会容易产生错误，这就导致基本不等式逐渐受到命题人的青睐.对于基本不等式内容而言，其主要是通过对函数的最值实施求解或实施证明，并通过文字对齐实施表述，即两个正实数的算数平均数大于或者等于其几何平均数.该部分内容通常在数学教学中占据着重要地位，且考试中的考查率极高.因此，在高中数学的具体教学中，教师需注重教材基础知识的讲解，引导学生对不等式的相关知识进行串联，充分掌握不等式的解题技巧，从而使学生的解题效率与正确率得到有效提高.

一、学生学习基本不等式的技巧

1.生活经验融入数学问题解决中

高中生学习的多数文化知识是相通的，没有哪门学科是单独存在的.因此，高中数学中基本不等式和其他知识也是相通的.在学生刚刚接触到基本不等式的时候，因为基本不等式存有多变性以及复杂性等特点，就会使学生无法及时的弄清楚不等式的相关知识，并生成相应的抵触心理.基于此，教师需注重学生内心的想法，并告诫学生基本不等式的题目并不难，需积极鼓励学生，给予学生足够的信心，积极应对基本不等式在具体学习当中出现的各种问题.同时，学生还需注重将相关生活经验融入到不等式问题的解决中，如将基本不等式的相关问题转变成三角形的两边之和大于第三边，且三角形两边之差小于第三边实施思考.

2.注重了解基本不等式的解题方法

对于不等式问题而言，由于其与等式问题存有较大的区别，学生只具备相应的计算能力，通常是无法解决基本不等式相关问题的.基本不等式虽然具有多变性以及复杂性，但是，对其根源进行追究，则能将其转变成最为简单的基本不等式.学生在解题的时候，最重要的就是简化不等式，因为不等式通常会转变成各种形式的问题，此时，就需学生注重自身审题技巧的提升，并找出试题当中隐藏的相关不等式，然后，教师引导学生对简化之后的不等式实施解题，其解题方法通常包含换元法、反证法等相关解题方法，并依据学生的实际状况，强化学生对各种解题方法的掌握熟练度，从而使学生做到灵活应用数学知识.

3.学生理解力与逻辑思维力的培养

想要使学生学习好基本不等式的相关知识，学生不仅需足够的认真仔细，而且还需具备相应的数学理解力以及逻辑思维力，由于基本不等式的相关问题已经无法通过简单计算进行解决，因此，学生在日常的学习时，需注重其数学理解力以及逻辑思维力的强化，从而实现轻松解题的目的与效果.

二、新课改下高中数学基本不等式解题技巧

1.反证解题技巧

在高中数学不等式解题中，反证的解题技巧已经得到广泛运用.通常而言，该技巧是用在正难则反的状况下，并在基本不等式的计算中，获得显著的效果.通过该解题技巧，不仅可以证明和基本不等式的有关问题，而且还能使基本不等式的证明过程更简单、便捷，以此实现解题效率的有效提高.

例如，已知：a+b+c>0，且ad+bc+ac>0，根据已知的条件，求解出a、b、c均大于0.

解析在对该问题进行求解前，需对试题实施详细的分析，因为a、b、c均大于0，那么，a、b、c三个数值就都不等于0，若a<0，且bc<0，那么，其能够满足条件a+b+c>0，同时，b+c>-a，最后所得的结果就是a(b+c)<0.需特别注意的是，根据题目的条件显示，ad+bc+ac+a(b+c)+bc<0，获得的该结果和题目条件之间相冲突，因此，上述的假设不成立，即a>0、b>0的同时，数值c也必须比0大，即完成证明.

2.性质解题技巧

利用基本不等式进行解题时，需注重对不等式的性质进行合理应用.具体来说，该解题方式就是最基础的，并能够应用于各种类型试题的解决中.如基本不等式具备传递性，即若a>b，且b>c，那么就表明a>c，除此之外，不等式还具有可加性特点，若a>b，则a+c>b+c，同理可知，在c>0时，有ac>bc，根据基本不等式具备的性质进行解题，不仅有助于学生迅速找到突破点，而且还能确保题目解答的正确率.

例如，已知，存有n个圆，且每个圆都会存有两点相交，且每三个圆都不会相交于同一个点.证明：n个圆能够将平面分为f(n)=n2-n+2个部分.

解析对公式f(n)=n2-n+2进行证明时，教师可引导学生通过归纳法进行解决.即当n=1的时候，f(1)=2，由此可知，n=1的时候，公式n2+n+2=2成立，因此，该命题是成立的.除此之外，教师也可引导学生将n设为k，且第k+1个圆的圆心以O进行表示，并根据试题题目的条件实施反续证明.经过上述的两种方式对基本不等式的题目进行解答，都能够证明f(n)=n2-n+2是成立的，在解题中，都是对不等式的性质进行合理应用，这不仅可以使基本不等式的题目难度得到有效降低，而且还能获得正确的结果，从而使学生的解题效率得到显著提高.

3.换元解题技巧

在对基本不等式进行分析的过程中，可将其式子当做整体，并对其中的变量实施替换，从而使基本不等式的问题解答更便捷与简单.换元解题的方法，通常又被称作为换元法，以此对不等式进行转化.该过程中，需注重构建元、置换元等两个要素.通常来说，换元法主要是通过等量代换作为基础的深入延伸，并对相关研究对象进行变换，以此对相关问题进行转移.除此之外，换元法通常还被称作为辅助元素法，也就是在基本不等式当中对全新变量进行引入，以此对分散条件进行综合处理，并将其中隐藏的相关条件凸显出来，或者是在具体解题的时候，将条件与结论相结合，以此形成学生所熟悉的结构，以便于后期的解题.

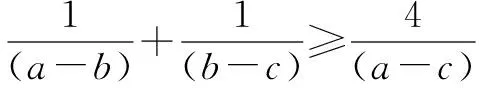
综上所述，高中数学的不等式教学中，学生只有熟练掌握不等式的解题技巧，确保学生在解题时具有正确的解题思路以及逻辑思维，才能促使学生的解题效率得到有效提高，实现数学成绩的提高，从而使高中生的数学素质以及知识应用能力得到有效提升.