带Lévy跳的随机SIQR模型的分析研究

刘世杰，刘茂省

（中北大学 理学院，太原 030051）

传染病是影响社会发展的重要问题，许多学者利用数学建模思想，根据疾病的传播机理建立了SI、SIR、SIV、SIQ等经典模型，对模型进行动力学分析，分析传染病的发展趋势并提出合理建议。对传染病的研究大多用确定性的系统来分析，但在疾病传播过程中仍然会有一些随机因素干扰［1－5］。文献中通常用白噪声来表示环境因素等的扰动，如气候、温度等，然而当遭遇重大自然灾害或突变（如地震、海啸、飓风或大型传染病等因素）时，在短时间内会改变种群规模，这种扰动的刻画是有一定难度的，研究者们提出用Lévy跳来描述刻画这些因素的影响［6－10］。

有很多学者对此类带Lévy跳的模型进行了分析，如Zhang等［8－10］分析了SIR、SEIR及艾滋病模型，得到了平衡点附近的渐近性质。Zhou等［11］研究了随机SIR模型，得到了疾病灭绝和存在的充分条件；Ge等［12］研究了具有非线性发生率的SIS模型，在得到疾病灭绝和存在充分条件的基础上还做出数值模拟，说明了随机扰动对传染病的影响。随着理论的发展和完善，也有更多模型出现，如Fan等［13－14］考虑将非线性发生率、时滞、白噪声和Lévy跳多种因素结合起来，得到疾病存在和灭绝的充分条件。

1 模型建立

考虑以下具有隔离的SIQR模型：

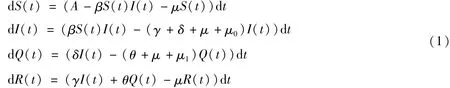
式中：S（t）代表易感者的数量；I（t）代表感染者的数量；Q（t）代表隔离者的数量；R（t）代表恢复者的数量；A为群体输入率；β为传染病的感染率；μ为自然死亡率；μ0和μ1分别为感染者和隔离者的因病死亡率；γ为感染者的恢复率；δ为感染者的隔离率；θ为隔离者的恢复率，以上所有参数均为正常数。由于系统（1）中的前3个等式不依赖于第4个等式，所以第4个等式可以省略。因此只考虑以下系统：

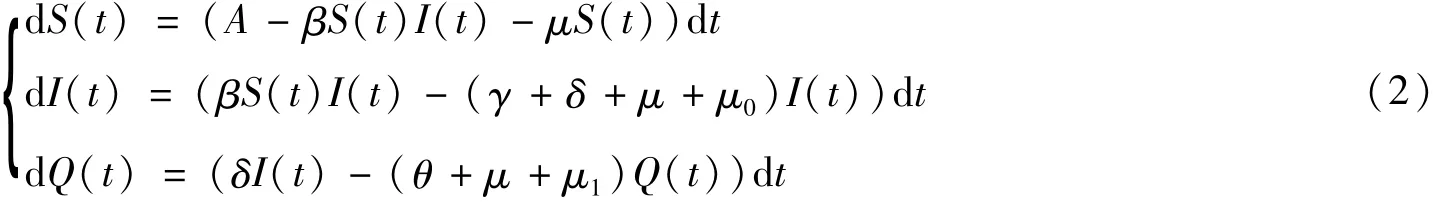
然而，在现实环境中，传染病的传播会受到很多环境因素的干扰，可以用白噪声来刻画这些因素。遭受地震、飓风、SARS等重大灾害时的干扰也是不可忽视的，因此，考虑一个带Lévy跳的随机模型：

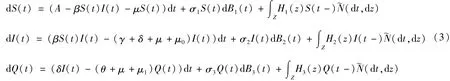
式中：标准布朗运动用B1、B2、B3表示；正常数σ1、σ2、σ3是其对应布朗运动的强度；Hi（z）＞－1，（i＝1，2，3）表示跳的强度。其中适应的鞅；N（t，U）是泊松随机测度；的补偿测度；n（d t，d z）＝E（N（d t，d z））是N（t，U）的强度测度，它满足n（d t，d z）＝π（d z）d t，其中π（d z）是Z上的测度，Z⊂（0，∞），π（Z）＜∞，以及满足以下条件：。值得注意的是，当随机扰动的强度为零时，系统（3）就是确定性的系统（2）。

2 全局正解的存在唯一性

3 解的渐近性质

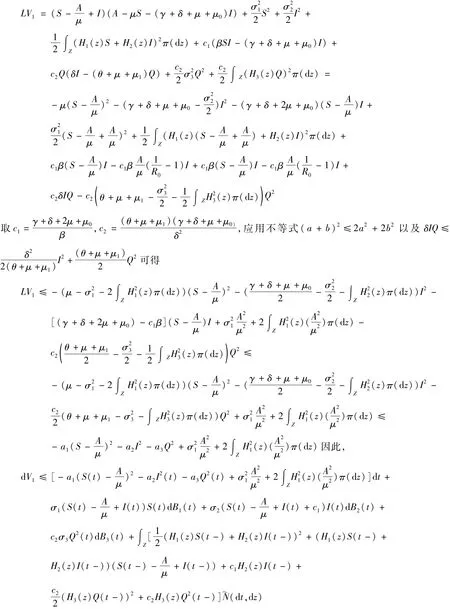
对上式两端从0到t积分后再求期望，有

0≤EV1［（S（t），I（t），Q（t））］≤EV1［（S（0），I（0），Q（0））］＋

定理3 若系统满足条件H1和H2，R0＞1，且满足

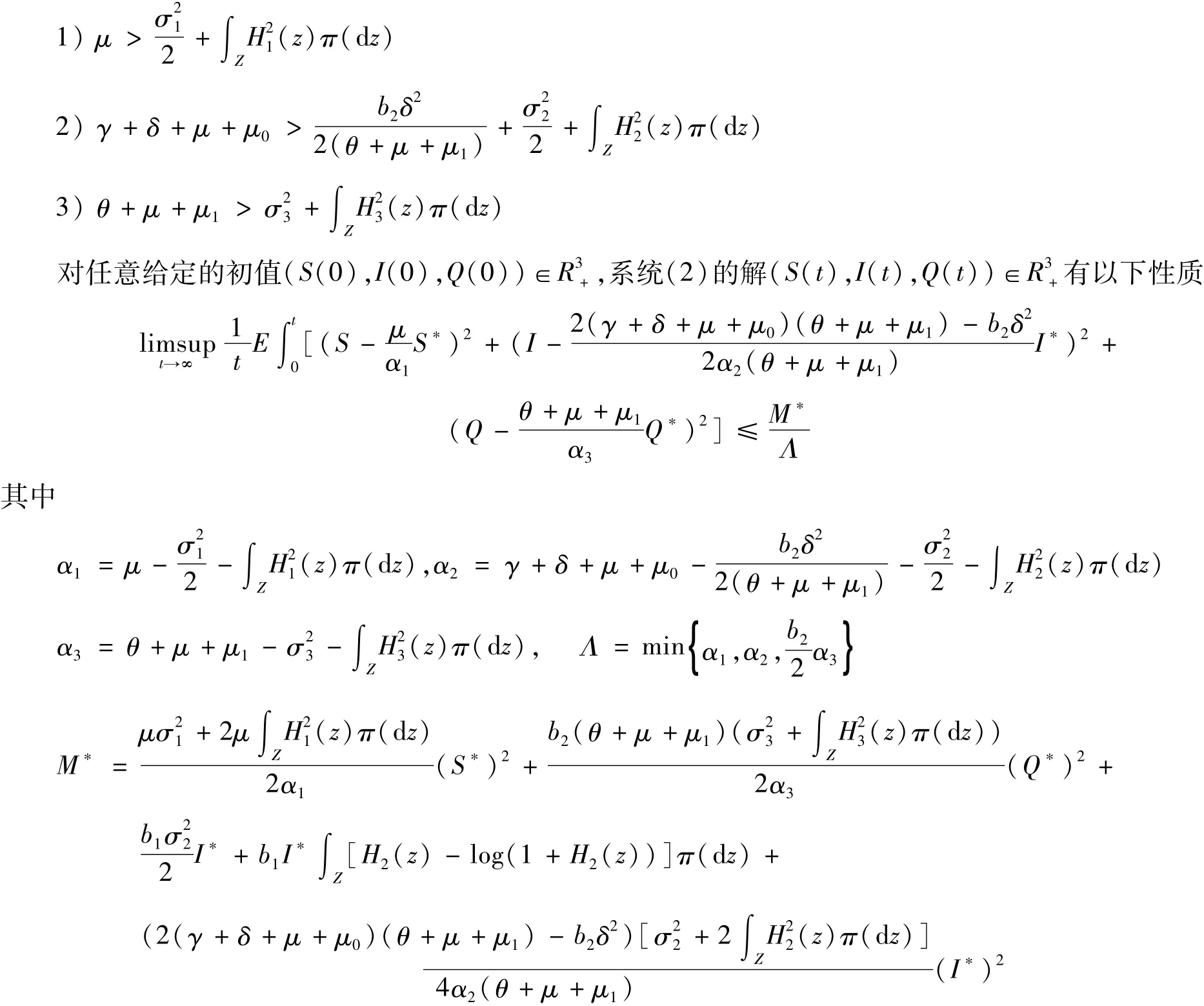
证：因为系统（2）对应的确定性模型存在唯一的正平衡点，所以有

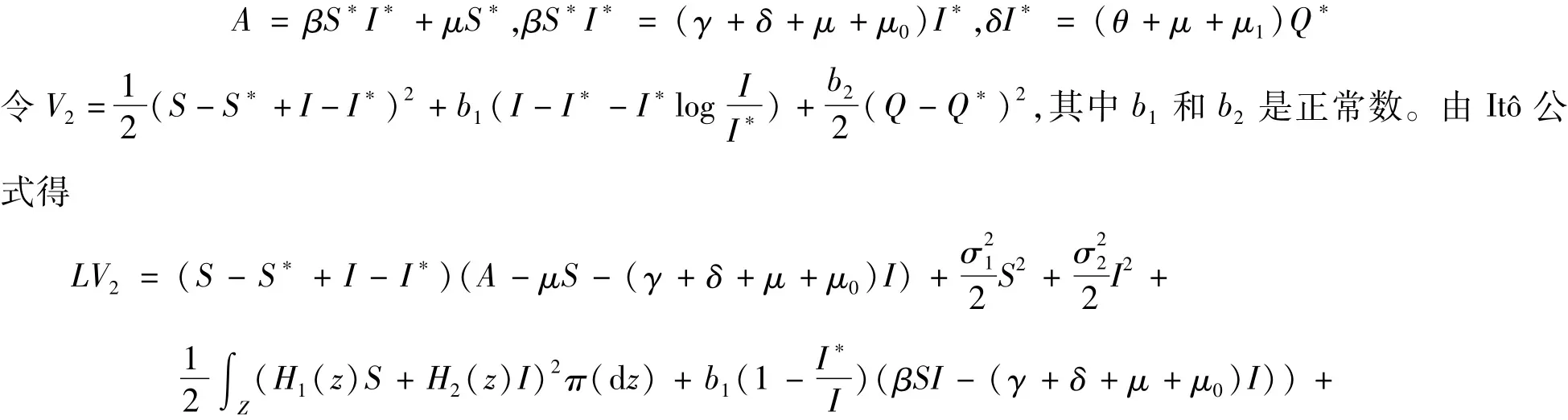
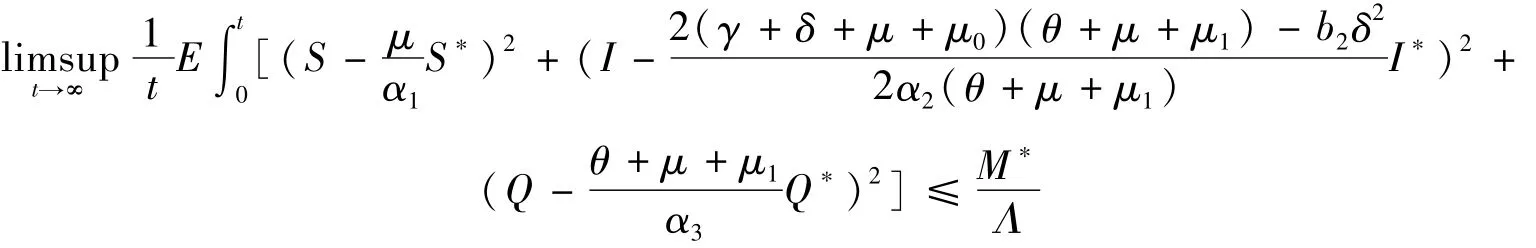
4 数值模拟

本节参考文献［18］和［19］，利用Matlab来验证理论结果。

1）对于系统（3），在系统（2）的无病平衡点附近，选定A＝0.3，β＝0.005，μ＝0.2，θ＝0.04，γ＝0.033，δ＝0.01，μ1＝0.03，μ0＝0.043，σ1＝σ2＝σ3＝σ4＝0.1，Z∈（0，∞），π＝0.8，H1（z）＝H2（z）＝H3（z）＝H4（z）＝0.2，且初值（S（0），I（0），Q（0），R（0））＝（0.5，0.2，0.1，0.1），易知R0＝0.026 2＜1，且满足定理2的其他条件，因此定理2成立，如图1所示。

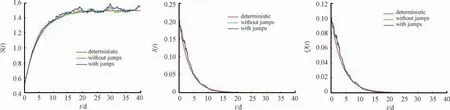
图1 R0＜1时确定性模型和随机模型解的渐近曲线

2）对于系统（3），在系统（2）的地方病平衡点附近，选定A＝0.3，β＝0.6，μ＝0.15，θ＝0.2，γ＝0.2，δ＝0.1，μ1＝0.1，μ0＝0.1，σ1＝σ2＝σ3＝σ4＝0.2，Z∈（0，∞），π＝0.1，H1（z）＝H2（z）＝H3（z）＝H4（z）＝0.1，且初值（S（0），I（0），Q（0），R（0））＝（0.5，0.2，0.1，0.1），易知R0＝2.1818＞1，且满足定理3的其他条件，因此定理3成立，如图2所示。

图2 R0＞1时确定性模型和随机模型解的渐近曲线

5 结论

研究了一类具有Lévy跳的随机SIQR模型的动力学行为，它能够更加准确反映突发情形下传染病的传播规律。首先分析了该系统具有全局正解，然后通过定理2、3分别讨论了带Lévy跳系统的解过程在原确定性系统的平衡点附近的渐近性态，随机系统的解过程在原确定性系统平衡点附近随机振荡，当改变Lévy跳的大小时，随机系统的解过程的振幅也会发生变化。研究结果表明：Lévy跳对疾病传播有一定的影响，有利于更好地研究传染病的动力学性态。将在未来的研究中考虑Lévy跳对其他传染病模型动力学性态的影响。