利用“隐形圆”解决动点最值问题

薛莲

摘 要：中考复习解决动点问题是难点，学生掌握较为困难，通过圆的有关知识来解决，让动点问题有迹可循，合理构建解题模型，运用几何图形的对称性，线段最短路径等性质，使学生突破解法障碍，提升解题技巧和方法。

关键词：隐形圆;折叠;解题技巧;最值

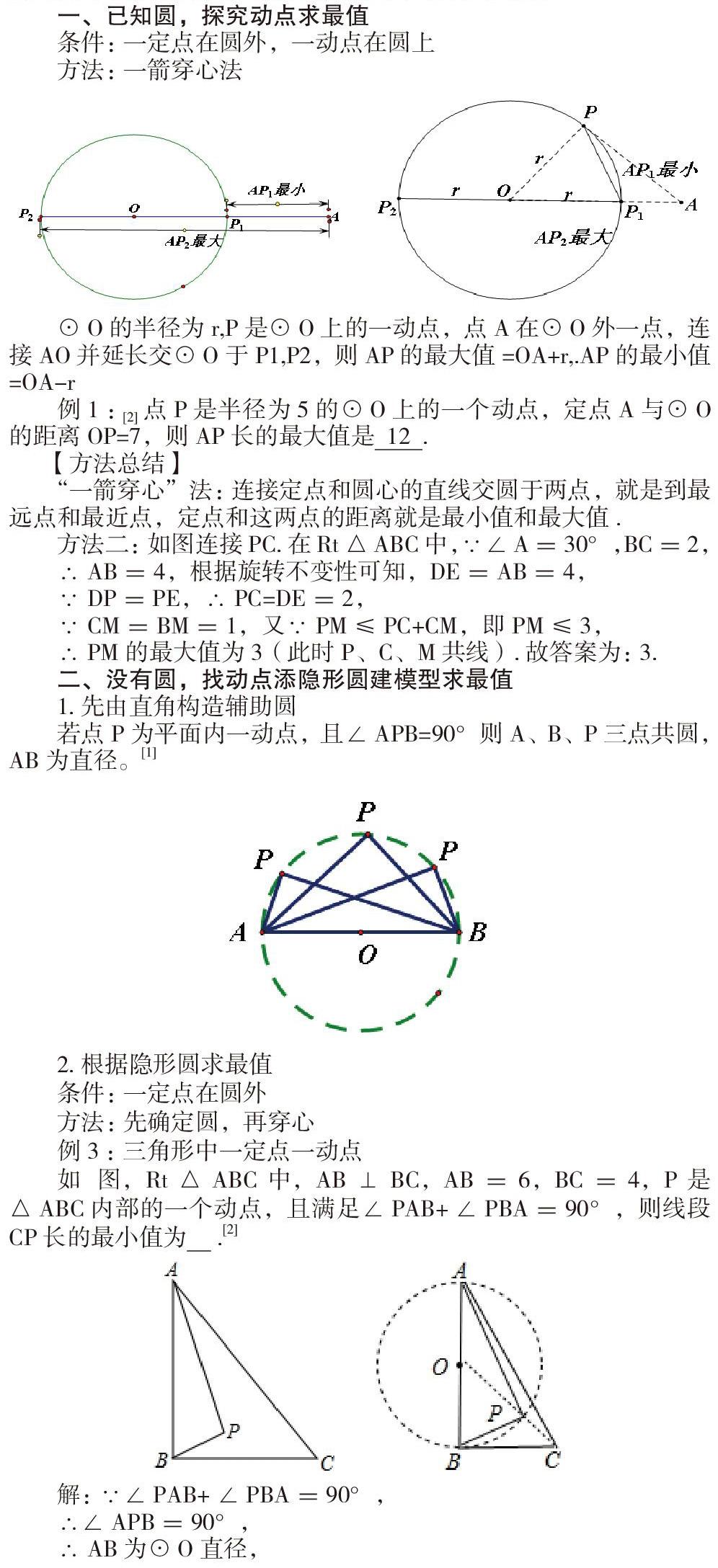
圆上动点近几年中考出现频率较高，有的给出圆，有的几何题没有直接给出圆，但能通过已知条件构造隐形圆，根据圆的有关知识借助图形的翻折、旋转、平移等的变换来找到定点和动点，从而求出最值问题，优化了解题的过程，使学生利用隐形圆模型解决动点问题有了新的认识，融会贯通处理中考难点问题。

三、结束语

动点问题中的求最值问题是中考数学中的高频题。本文从问题的形成发展中寻找规律，教学中，教师积极的带领学生体验积累过程中的学习经验，培养学生动态的数学学习观，最值问题中的“最”字隐藏着唯一与无数不是孤立的存在，它是对比的结果。在日常教学中，教师要强化数学的建模意识，提炼归纳总结出数学模型，让学生学会把复杂的问题，转化为简单问题，从而提高了学生的解题能力及学习数学的兴趣。数学解题教学不应该是“授人以鱼”式的解题模式，而是教会学生探究解题本源的“渔趣”，从而激发挖掘出学生学习数学的潜能。

总之：从已知条件入手，可以提升数学综合知识信息的能力，产生多种解题思路，若能根据题目条件，联想到圆的有关知识，构造出隐形圆模型，这样可以化难为易，化繁为简，化隐为显，找到解题思路和方法，培养学生独立思考能力，学生才能在潜移默化中学会用数学的眼光看世界，会用数学思维思考世界。

参考文献：

[1]喻俊鹏. 中考试题中的双动点型问题解析[J]. 中学数学教学参考：教师版， 2004， 000（001）：111-113.

[2]陆祥雪. 应用定点到圆上点的距離特性解题[J]. 中学生数学， 2014（9）：38-39.

[3]吴键. 聚焦四边形考点及亮点题型[J]. 试题与研究：中考， 2016， 000（002）：27-33.