基于散焦信息的纱线毛羽三维测量与验证

李忠健 董龙 倪海云 王静安 王鸿博 邹专勇

摘要： 毛羽是衡量纱线质量好坏的重要指标，然而现有毛羽检测中难以快速获得其三维长度（毛羽空间轨迹长度）。文章提出了在获得单幅图像的基础上准确表征纱线毛羽空间长度的方法。采用远心镜头获取纱线毛羽图像，经过同态滤波、直方图均衡化、边缘增强、水平集分割等处理，获得包含空间信息的毛羽分割图像。结合散焦成像原理，建立毛羽宽度、灰度与其空间深度之间的模型关系，实现毛羽空间三维长度的快速测量。基于单幅散焦信息的毛羽空间长度测量，为实时三维检测奠定基础。实验结果表明，文章所提方法可有效实现清晰与模糊区域毛羽的分割，所测毛羽三维长度与人工测量结果相近。

关键词： 毛羽三维长度;单幅图像;散焦信息;图像分割;深度恢复;毛羽检测

中图分类号： TS103.7

文献标志码： A

Abstract： Hairiness is an important indicator to measure the quality of yarn. However， it is difficult to quickly obtain its three-dimensional length（space trajectory length of hairiness） in the existing hairiness test. In this paper， we propose a method to accurately characterize the three-dimensional length of yarn hairiness based on single images. A telecentric lens is used to obtain the hairiness image of yarns， and after homomorphic filtering， histogram equalization， edge enhancement， level set segmentation， etc.， a segmentation image of hairiness which contains spatial information is obtained. Combined with the principle of defocus imaging， the model relationship between hairiness width， gray scale and its spatial depth is established to achieve the quick measurement of the three-dimensional length of hairiness in space. The spatial length measurement of hairiness based on the defocus information of single images lays a foundation for real-time 3D detection. The experimental results show that the proposed method can effectively achieve the segmentation of hairiness in clear and fuzzy areas， and the measured three-dimensional length of hairiness is close to the results of manual measurement.

Key words： 3D length of hairiness; single image; defocus information; image segmentation; depth recovery; hairiness detection

毛羽作為评定纱线质量最重要的指标之一，其数量及长短不仅直接决定了纱线的外观、质量和等级，而且当毛羽分布不匀或者长毛羽较多时，会使织机开口困难，染色不匀，降低织造和染色工序生产率，造成织物质量下降，使企业难以生产出优质的纺织品[1-3]。目前毛羽的检测主要采用光电式分级统计法的毛羽根数分布指标和光电式全毛羽法的毛羽H值指标进行表征，是当前占主导地位的测量方法。然而由于光电传感器本身的限制，其检测精度较低，测量结果为统计指标，无法表征单根毛羽的信息，更不能直观反映毛羽的空间形态[4-8]。随着机器视觉技术的不断发展，利用图像技术检测纱线毛羽的研究逐渐成为热点[9-10]，主要通过采集纱线图像，结合图像处理算法，测量毛羽到纱线主干边缘的距离、毛羽面积等参数，包括基于二维平面信息图像测量和基于多幅的三维测量。从测量原理来看，图像法无论在精度，还是准确度都要优于光电法，且可对单根毛羽的轨迹进行表征。但是，二维平面信息法[11-18]检测的是空间毛羽在某个平面的投影长度，并

不是毛羽实际长度，且测量结果与毛羽的弯曲状态有关，误差较大;多幅三维测量是利用相机拍摄两个镜子中的纱线[5-6]或拍摄旋转的纱线[7-8]，并进行立体重建实现毛羽的三维检测，但该法受重建效率及纱线旋转效率的影响，较难达到纱线毛羽的三维实时测量，限制了其在纱线检测中的应用。

本文针对目前纱线毛羽检测存在的问题，提出通过从单幅散焦图像中恢复毛羽深度信息，并根据分割结果追踪毛羽空间长度，实现毛羽的三维快速、实时测量，避免三维重建的高复杂度和耗时性，为毛羽在线监测的智能化、精确化开辟新途径，对纺纱、织造等生产过程有重要的实践指导作用。

1 图像采集与预处理

1.1 图像采集

为连续获取纱线图像及快速标定深度距离，自行开发了距离可调型图像式纱线外观参数检测系统，如图1（a）所示。其中，图像采集设备采用度申科技M3ST130-H相机及物方远心镜头，图像采集帧频为213 fps，图像大小为1 280 dpi×1 024 dpi，其中1个像素点大小为0.001 3 mm。图1（a）中，相机与纱线间的距离可根据需要进行调节，以方便深度的标定，伺服电机可根据脉冲信号实现纱线的连续采集，获取的单幅纱线图像如图1（b）所示。

1.2 图像预处理

从图1（b）纱线形态构象可以看出，毛羽是一种在空间易发生卷曲和弯曲的线状目标。由于光照、背景及毛羽本身的易彎曲特性，空间毛羽成像后的图像清晰度通常随其位置而变化，且目标离聚焦位置越远，图像模糊程度越大，目标与背景也越相似，基于该模糊信息与目标位置的关系，可用于毛羽的三维测量。因此，对毛羽图像中清晰与模糊区域进行准确分割，精准定位毛羽模糊宽度，是测量毛羽三维长度的关键。为实现毛羽图像的分割，采用以下算法流程对图像进行预处理。

1.2.1 同态滤波

同态滤波是一种典型的非线性滤波系统，能够在频域中

对图像对比度进行增强和对图像进行压缩，从而提高图像亮度。一幅图像f（x，y）可以用照明分量i（x，y）与反射分量r（x，y）的乘积来表示，即：

f（x，y）=i（x，y）×r（x，y）（1）

对式（1）进行两边取对数、傅里叶变换、低通滤波、指数运算等处理实现同态滤波[19]，获得增强图像g（x，y）：

g（x，y）=eH（u，v）F（lnf（x，y））=eH（u，v）F（lni（x，y））eH（u，v）F（lnr（x，y））（2）

同态滤波可减少低频增加高频，减少光照变化对图像的影响，并对图像的边缘细节进行锐化，图1（b）滤波后的效果及其直方图如图2所示。

1.2.2 直方图均衡化

从图2可以看出，虽然纱线目标与背景具有一定的对比度，但纱线图像整体偏黑，图像直方图的分量集中在灰度较低的一端。为使目标更加突出，图像灰度值趋于均匀分布，将图2（a）依据式（3）进行直方图均衡化[20]，获得更亮、对比度更高的图像，如图3所示。

Sk=T（rk）=∑kj=0njN（3）

式中：Sk表示直方图均衡化后各像素的灰度级;rk=k/（L-1）表示归一化后的灰度级，k=0，1，2，…，L-1表示归一化前的灰度级;L表示图像中的最大灰度值;nj表示图像中灰度级为j的像素个数;N表示图像中像素的总数。

1.2.3 边缘增强

单幅纱线图像中散焦模糊区域与清晰区域并存，散焦形成的模糊宽度与灰度对深度的计算至关重要，而边缘的清晰程度直接影响模糊宽度的测量，因此需要对目标物体边缘进行增强处理。梯度图像在沿目标对象的边缘处有较高的像素值，而在其他地方则有较低的像素值，结合Sobel算子，分别求图3（a）水平方向和竖直方向的偏导数，获得梯度图像，如图4所示。图4中，模糊与清晰区域中目标的边缘都较清晰，有利于毛羽边缘的精确定位。

2 模型构建与三维测量

2.1 空间深度恢复模型构建

当相机获取场景图像时，根据点光源成像模型及薄凸透镜的成像原理，当某点不在聚焦平面时，其光线经相机光圈在成像平面上会产生模糊现象，且该模糊量的大小与物体位置点离聚焦平面间的距离有关[23]。因此，通过对模糊量进行测量可恢复出物体的深度信息。为探索毛羽模糊量与深度之间的关系，考虑实际成像中受光学像差、衍射、图像放大率等因素的影响，采用远心镜头对图像进行获取，建立毛羽空间深度与模糊宽度、灰度之间的数学模型。对基于薄透镜模型的物方远心镜头成像光路图进行绘制，以毛羽在聚焦平面位置后为例，如图6所示。

图6中，设f为焦距;U、V为聚焦时物距和像距;D表示凸透镜有效镜片直径（光圈大小）;W0是物体的实际宽度，即毛羽的直径;W是聚焦时成像平面上纤维的宽度;U′是移动物体后新的物距;V′为新聚焦时的像距;W′是像面上新的纤维宽度，即模糊宽度。

对图7进行分割，并测量其宽度值和灰度平均值，依据最小二乘原理拟合深度与宽度、灰度的函数关系，如图8所示。根据该函数关系应用于获取的所有单幅纱线图像，进一步结合分割出的毛羽宽度和灰度即可映射出对应的深度值。

从图8（a）可以看出，靠近和远离镜头相同位置获取的图像亮度存在一定的区别，因此根据该区别唯一确定纱线图像中散焦模糊的歧义性。图8（b）对远离镜头部分中深度与宽度、灰度的函数关系进行拟合，获得函数关系式（8），相关系数R2达0.998，可用于毛羽空间深度的准确计算。

从图9可以看出，v值的变化对图像分割效果影响不大，也就是v值的优选可在一个较大的范围选择。这是由于纱线毛羽图像经历了多步骤的预处理，使毛羽边界与背景区分明显，因而在分割时Chan-Vese模型对v值的依赖较小。

3.1.2 迭代次数iter的影响

在Chan-Vese模型中，迭代次数不仅对图像分割效果产生重大影响，同时严重影响分割的执行时间。保持v不变，iter=200、600、1 000、2 000时，图4的分割效果与运行时间（Windows 10，i5，8G，Matlab R2014b）的结果如图10所示。

从图10可以看出，随着迭代次数增加，分割效果越好，同时分割所用时间也越长。因此，在综合分割效果与效率的基础上，选用iter=1 000对毛羽图像进行处理。

3.2 毛羽测量结果验证

根据图5毛羽分割结果，利用形态学运算去除毛羽条干，并将毛羽进行细化获得毛羽中心线图像，如图11（a）所示。结合毛羽中心线位置和毛羽轮廓线（图11（b）），计算分割出的毛羽的宽度，如图11（c）所示。最后，根据式（8）和（9）映射毛羽空间深度值并得到毛羽三维长度。

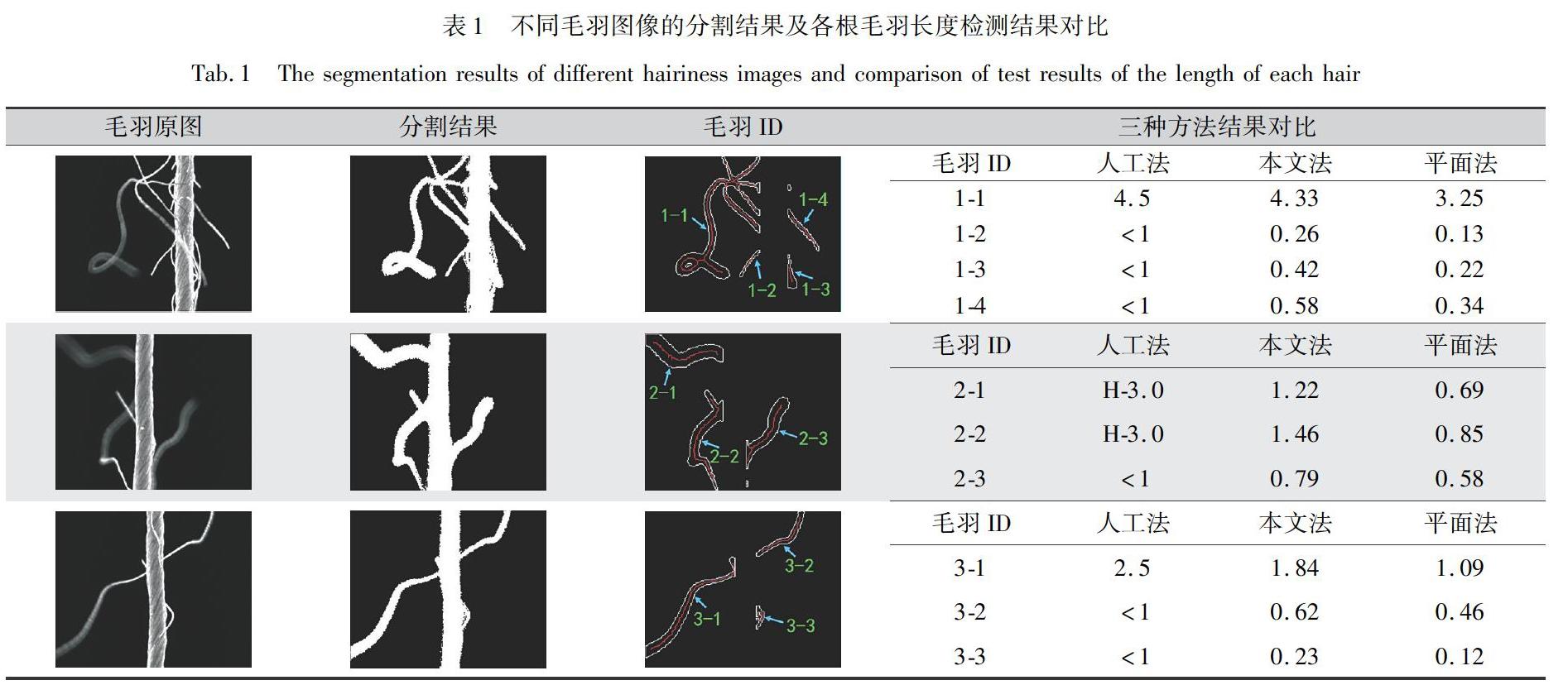
利用上述方法对系列图像进行处理，并计算各根毛羽三维长度，将获得的结果与手动测量结果进行对比，如表1所示。表1中，第1列为纱线毛羽原图，第2列为图像分割结果，第3列为去除条干后毛羽的轮廓及其中心线图并标示有各根毛羽ID，第4列为各幅图像中各根毛羽长度的三维测量与人工法和平面法结果的对比表（长度单位为mm），其中人工法采用的是拉直毛羽尺子測量的方法，平面法为根据分割结果直接计算毛羽长度的方法（即空间毛羽在平面上的投影）。

从表1可以看出，本文所提毛羽分割算法可将模糊毛羽与清晰毛羽清楚地分割出来;毛羽测量结果中，所提方法测量的毛羽长度明显比平面法要长，这是由于平面法获取的图像中的毛羽是真实毛羽的投影，故结果要比实际长度更短;与人工测量的毛羽结果相比，所提方法的三维长度结果与人工法接近，但也存在一定差异性，如毛羽ID 2-1和2-2的毛羽真实为1根毛羽，但本文方法检测为2根;同时毛羽ID 1-1毛羽真实情况为多根毛羽的交叉连接等，但本文方法检测为1根毛羽。因此，本文所提毛羽三维测量方法可获得一定情况下与人工法接近的结果，但计数时是否为同一根毛羽具有一定的误差。

4 结 论

本文提出了一种基于单幅图像散焦信息的毛羽空间三维长度测量方法，利用远心镜头获取纱线毛羽图像，经过同态滤波、直方图均衡化、边缘增强、水平集分割处理，获得包含空间信息的毛羽分割图像;结合散焦成像原理，建立毛羽宽度、灰度与空间深度之间的模型关系，以靠近和远离镜头获得的条纹板图像数据进行训练，获得模型参数;将图像分割出的宽度和灰度带入模型中，实现毛羽空间三维长度的测量。实验结果表明，与人工法和平面法测量结果相比，所提方法与人工测量结果接近，但同一根毛羽的确定存在较大误差。因此，本文可在获取一幅图像的基础上实现毛羽的三维测量，避免多幅图像重建的耗时性和复杂性，为纱线毛羽的快速准确测量奠定基础，克服了传统光电和电容法的二维局限性。在后续的研究中，将深入对毛羽轨迹的追踪、毛羽与毛羽间、毛羽与条干间的相互遮挡问题展开研究，持续优化毛羽空间三维长度测量方法。

参考文献：

[1]于伟东. 纺织材料学[M]. 2版. 北京： 中国纺织出版社， 2018： 218-260.

YU Weidong. Textile Materials Science[M]. 2nd Edition. Beijing： China Textile Press， 2018： 218-260.

[2]杨红英， 朱苏康. 纱线毛羽[J]. 纺织学报， 2000， 21（6）： 11-14.

YANG Hongying， ZHU Sukang. Yarn hairiness[J]. Journal of Textile Research， 2000， 21（6）： 11-14.

[3]肖琪， 王瑞， 陆鑫， 等. 基于布面毛羽长度和毛羽密度的涤棉混纺机织物起球倾向[J]. 丝绸， 2020， 57（9）： 27-33.

XIAO Qi， WANG Rui， LU Xin， et al. Pilling tendency of polyester/cotton blended woven fabric based on fabric hairiness length and hairiness density[J]. Journal of Silk， 2020， 57（9）： 27-33.

[4]李汝勤， 宋钧才， 黄新林. 纤维和纺织品测试技术[M]. 上海： 东华大学出版社， 2015： 29-90.

LI Ruqin， SONG Juncai， HUANG Xinlin. Fiber and Textile Testing Technology[M]. Shanghai： Donghua University Press， 2015： 29-90.

[5]WANG L， XU B， GAO W. Multi-perspective measurement of yarn hairiness using mirrored images[J]. Textile Research Journal， 2018， 88（6）： 621-629.

[6]WANG L， XU B， GAO W. Three-dimensional measurement of yarn hairiness via multiperspective images[J]. Optical Engineering， 2018， 57（2）： 1-9.

[7]WANG W， XIN B， DENG N， et al. Objective evaluation on yarn hairiness detection based on multi-view imaging and processing method[J]. Measurement， 2019（148）： 1-8.

[8]王文帝. 自旋转式图像法纱线毛羽数字化检测及其应用[D]. 上海： 上海工程技术大学， 2020.

WANG Wendi. Detection and Application of Yarn Hairiness by Digital Self-Rotating Image Method[D]. Shanghai： Shanghai University of Engineering Science， 2020.

[9]付國定， 陈桦， 刘红， 等. 数字图像处理技术在纺织服装领域的研究进展[J]. 丝绸， 2011， 48（12）： 22-25.

FU Guoding， CHEN Hua， LIU Hong， et al. Overview of research on image processing technology in textile and clothing field[J]. Journal of Silk， 2011， 48（12）： 22-25.

[10]卢雨正. 竹节纱织物竹节分布均匀性评价方法[J]. 丝绸， 2012， 49（4）： 33-36.

LU Yuzheng. Evaluation method for the slub distribution evenness in the slubby yam fabric[J]. Journal of Silk， 2012， 49（4）： 33-36.

[11]FABIJAN′SKA A. Yarn image segmentation using the region growing algorithm[J]. Measurement Science & Technology， 2011， 22（11）： 114024.

[12]ZHANG G， XIN B. An overview of the application of image processing technology for yarn hairiness evaluation[J]. Research Journal of Textile & Apparel， 2016， 20（1）： 24-36.

[13]SUN Y， PAN R， ZHOU J， et al. Analysis of detectable angles of yarn hairiness in optical measurements[J]. Textile Research Journal， 2017， 87（11）： 1297-1307.

[14]JING J， HUANG M， LI P， et al. Automatic measurement of yarn hairiness based on the improved MRMRF segmentation algorithm[J]. Journal of the Textile Institute， 2018， 109（6）： 740-749.

[15]孙巧妍， 陈祥光， 刘美娜， 等. 基于毛羽补偿与自适应中值滤波的纱线主体图像识别算法[J]. 纺织学报， 2019， 40（1）： 62-66.

SUN Qiaoyan， CHEN Xiangguang， LIU Meina， et al. Image recognition algorithm based on yarn hairiness compensation and adaptive median filter[J]. Journal of Textile Research， 2019， 40（1）： 62-66.

[16]李鹏飞， 严凯， 张缓缓， 等. 基于最大熵与密度聚类相融合的毛羽检测[J]. 纺织学报， 2019， 40（7）： 158-162.

LI Pengfei， YAN Kai， ZHANG Yuanyuan， et al. Hairiness detection based on maximum entropy and density clustering[J]. Journal of Textile Research， 2019， 40（7）： 158-162.

[17]景军锋， 宁小翠， 李鹏飞， 等. 交叉毛羽的凹点匹配分割算法[J]. 毛纺科技， 2019， 47（5）： 1-5.

JING Junfeng， NING Xiaocui， LI Pengfei， et al. The cross hairiness segmentation algorithm based on the pits matching[J]. Wool Spinning Technology， 2019， 47（5）： 1-5.

[18]LI Z， ZHONG P， TANG X， et al. A new method to evaluate yarn appearance qualities based on machine vision and image processing[J]. IEEE Access， 2020（8）： 30928-30937.

[19]GONZALES R C， WOODS R E. Digital Image Processing[M]. 3rd Edition. NJ： Prentice Hall， 2007.

[20]左飞. 数字图像处理： 原理与实践（MATLAB版）[M]. 北京： 电子工业出版社， 2014.

ZUO Fei. Digital Image Processing： Principles and Practice（MATLAB Edition）[M]. Beijing： Publishing House of Electronics Industry， 2014.

[21]CHAN T F， VESE L A. Active contours without edges[J]. IEEE Transaction on Image Processing， 2001， 10（2）： 266-277.

[22]LIU S， PENG Y. A local region-based chan-vese model for image segmentation[J]. Pattern Recognition， 2012（45）： 2769-2779.

[23]PENTLAND A. A new sense for depth of field[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 1987， 9（4）： 523-531.

[24]WANG J G， XU B G， LI Z J， et al. Depth recovery of hairy fibers for precise yarn hairiness measurement. [J]. Applied Optics， 2018， 57（24）： 7021-7029.