基于风险等级的中小微企业信贷模型研究
2021-08-05顾一凡黄莉媛林晨欣曹春萍
顾一凡 黄莉媛 林晨欣 曹春萍


摘 要:为切实解决中小微企业贷款融资和银行对中小微企业贷款策略之间存在的问题,提出了基于风险等级的中小微企业信贷模型。该模型创新性地将机器学习算法引入传统中小微企业信贷风险及策略的研究当中,运用PCA降维、K-means聚类确定企业风险等级;通过Fisher线性判别确定银行信贷利率。应用该模型将123 家中小微企业分成五类风险等级,并给出银行对五类不同风险等级企业的贷款额度及利率,并通过实验验证模型的有效性和正确性。
关键词:K-means聚类;PCA降维;Fisher线性判别;信贷模型
中图分类号:TP391 文献标识码:A
Research on the Credit Model of Small, Medium and
Micro Enterprises based on Risk Level
GU Yifan1, HUANG Liyuan2, LIN Chenxin2, CAO Chunping1
(1.School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China;
2.Business School, University of Shanghai for Science and Technology, Shanghai 200093, China)
guyifan2020@126.com; 948384993@qq.com; 1246506991@qq.com; 2213893844@qq.com
Abstract: In order to effectively solve the problems between loan financing of small, medium and micro enterprises and the bank's loan strategy for them, this paper proposes to build a credit model for small, medium and micro enterprises based on risk level. This model innovatively introduces machine learning algorithms into the research on credit risks and strategies of traditional small, medium and micro enterprises. PCA (Principal Components Analysis) dimensionality reduction and K-means clustering are used to determine enterprise risk level. Bank credit interest rate is determined by Fisher linear discriminant. Based on this model, 123 small, medium and micro enterprises are divided into five risk levels, and the bank's loan lines and interest rates for each level are given. Validity and accuracy of the model are verified through experiments.
Keywords: K-means clustering; PCA dimensionality reduction; Fisher linear discriminant; credit model
1 引言(Introduction)
中小微企业作为我国宏观经济的“毛细血管”,贡献了我国80%的就业岗位和60%的GDP[1-2]。但中小微企业自身资金实力弱,若想发展就需要获得银行提供的贷款支持,而银行放贷首要考虑的是贷款资金的安全,因此银行放贷资金安全与中小微企业贷款需求之间的矛盾便成为一个亟待解决的问题。
目前,银行为了解决这一问题,采取了如下策略:对中小微企业进行风险评估,对于风险等级在一定标准下的企业,给予放贷。在郑建华等[3]提出的研究企业信用评级模型中,使用了层次分析法进行评级模型的构建。在郝晓露等[4]提出的商业银行贷款的研究中,使用了灰色预测模型对贷款利率进行了预测。王薛[5]使用了AHP——模糊综合评价农村信用社农户贷款风险模型。仔细分析上述模型可以发现,每个模型都涉及大量计算和推断。计算机在大量数据的计算中表现出了极大的优势,所以构建基于计算机的信贷模型成为目前的研究热点。
本文在郑建华等相关工作的基础上,创新性地将机器学习算法引入对中小微企业贷款风险的研究当中。针对这一问题,提出了基于中小微企业风险评估等级的银行贷款模型。该模型首先从企业原始发票信息中提取若干指标;其次通过对指标进行降维,对企业进行聚类,划分出企业风险等级;最后根据企业对应的风险等级,通过构建贷款额度与贷款利率的计算模型,为银行制定相应的贷款策略。
2 企业风险等级确定(Enterprise risk level determination)
从123 家企业的进项、销项发票记录中提取信息,定义10 个原始风险评价指标[6-7]。将这10 个原始风险评价指标通过PCA降維,得到三个降维之后的评价指标,既保留了原始数据的绝大部分信息,又极大简化了后续的计算量。最后,根据三个降维之后的评价指标,通过K-means聚类,将原123 家企业分为五个风险等级,为后续银行信贷策略的确定提供依据。
2.1 原始评价指标定义
从123 家企业的进项、销项发票记录中,提取并定义企业实力及企业信誉两大类共10 个评价指标。
企业实力评价指标如下定义:
:企业有效销售次数;
:企业有效进货次数;
:企业供应稳定性,即有效进货次数与总体进货次数的比值;
:企业销售稳定性,即有效销售次数与总体销售次数的比值;
:企业进货规模,即进项金额总和(营业成本);
:企业销售规模,即销项金额总和(营业收入);
:企业对上游企业的影响力,即企业销方销售总额;
:企業对下游企业的影响力,即企业购方采购总额。
企业信誉评价指标如下定义:
:企业信用评级,即将企业A、B、C、D四档原始信用评级折算为4321分值;
:企业违约情况,即若企业有违约记录,则该指标为1,否则为0。
2.2 基于PCA降维对原始指标进行简化
主成分分析通过正交变换的方法,将原始线性相关的观测数据转变为若干个线性无关变量表示的数据[8]。线性无关的变量称为主成分。如此,将原来高维空间中的数据映射到低维空间,降低了计算复杂度。同时,保留了原始数据中的大部分信息,实现了数据降维的功能。
如上10 个指标覆盖了123 家企业各个方面的信息,可以较为全面地量化其内在的风险。但由于这10 个原始指标所构成的高维数据不便于观察和计算,所以采用PCA降维对原始高维指标进行降维。通过计算10 个信贷风险指标之间的相关系数矩阵,再求解相关系数矩阵的特征值与特征向量。将特征向量对应主成分的特征值与全体特征向量对应主成分的特征值之和的比值定义为信息贡献率,选取前三个贡献率最大的主成分,其贡献率依次为34.85%、20.22%、13.42%,累积贡献率达68.49%,可以最大程度保留原始10 个指标中所包含的企业内在风险的信息,又能解决高维指标数据不便于观察计算的问题。
其中第一主成分为:
(1)
第二主成分为:
(2)
第三主成分为:
(3)
将式(1)第一主成分定义为企业交易规模指标,式(2)第二主成分定义为企业信誉指标,式(3)第三主成分定义为企业盈利能力指标。从三个维度重新审视企业内在的风险等级。
2.3 基于K-means确定123 家企业的风险等级
K均值聚类是常用的聚类算法。在未知数据特征标签的情况下,将各项指标接近的样本点聚成一类[9]。首先,由已确认的分类个数选择个数据对象作为初始聚类中心;然后将其余样本点分配到与之最近的聚类中心所在的类中;进而更新每个类中样本点的均值作为下一次更新的聚类中心。如此往复迭代,直至聚类结果收敛为止。K-means算法流程如图1所示。
将简化后的指标作为训练数据,通过K-means聚类,将123 家企业聚类成不同风险等级的类别。选取=5,将原始123 家企业依据降维之后的三个指标分成五个风险等级:高风险企业、较高风险企业、中等风险企业、较低风险企业、低风险企业。以此完成对123 家企业风险等级的确定。
3 银行信贷模型(Bank credit model)
银行信贷模型分成银行信贷额度确定和银行信贷利率确定两大部分。依据企业有效进货次数等三个指标,通过Fisher线性判别预测企业信贷违约概率。根据企业信贷违约概率建立银行信贷额度求解模型。同时,依据银行信贷利率与不同信誉等级下的客户流失率的统计数据进行数据拟合,再结合企业信贷违约率等相关数据,建立银行信贷利率求解模型。
3.1 基于Fisher线性判别的企业违约率预测[10]
Fisher线性判别是一种经典线性判别方法,适用于二分类问题。其核心思想为训练一组样本点,将样本点投影到一条直线上,使得同类样本点的投影点尽可能密集接近,使得异类样本点的投影点尽可能远离。最终训练出一个模型进行线性判别预测,同时给出样本点所属对应两个类别的概率。
由于无法从企业过往违约情况中直接得到企业未来贷款偿还的违约率,故采用Fisher线性判别,基于企业有效进货次数、有效销售次数、企业信用评级作为训练数据训练模型。将企业未来是否违约转化为一个二分类预测问题,即将企业划分为未来会违约的组别和未来不会违约的组别,将预测结果与企业过往违约情况进行比对,得到得分模型:
(4)
若得分>0,则将该企业预测为不违约;反之,则将该企业预测为违约。由于样本点的分类存在属于对应类别的概率,故将样本点属于违约类别的概率定义为该企业的违约概率,将该样本点属于未违约类别的概率定义为该企业的不违约概率。
3.2 银行信贷额度的确定[11]
原则上不为信誉评级为D的企业发放贷款,故额度模型的建立及之后的计算中,自动剔除信誉评级为D的企业。设银行年度贷款总额为固定常数元,计算同一风险等级企业的平均贷款额度为:
(5)
其中,为级企业的平均不违约概率,为级下企业总数(不包括信誉评级为D的企业)。
3.3 银行信贷利率的确定[12]
本文贷款利率求解步骤如下:
步骤1:根据银行贷款年利率与不同信誉等级下客户流失率的统计数据,进行对数函数形式的曲线拟合,得到如式(6)所示的银行客户流失率与贷款年利率之间的函数关系。
(6)
其中,表示第类风险等级且信誉等级为的企业的流失率,表示第类风险的贷款年利率。由于不包含风险等级为D的企业,故如上函数中,没有的函数关系式。
步骤2:可表示为第类风险等级且信誉等级为的企业的留存率,将式(6)代入,则第类风险等级企业的总体流失率如式(7)所示。
(7)
其中,表示第类风险等级且信誉等级为的企业个数。
步骤3:以为决策变量建立如式(8)所示非线性规划模型。
(8)
其中,为第类风险等级的企业贷款利率,目标函数表示银行的总收入,表示给第类风险等级企业贷款的总额度,企业贷款利率的约束条件为4%至15%。
通过对式(8)非线性规划函数模型在约束条件下求解,可以得到在风险可控的情况下,在贷款利润最大化的前提下,银行贷给不同风险等级企业的各自贷款利率。再结合由式(5)计算得到的不同风险等级下,银行给企业贷款的額度,可以完整给出银行对于不同风险等级下的企业的贷款策略。由于同一风险等级下企业的风险情况近似相等,故按照风险等级组别给出策略,可以极大降低放贷的复杂程度,同时保证风险可控。
4 实验验证(Experiment verification)
4.1 实验数据集
本次研究所用数据集包括四个:企业信息数据集、进项发票信息数据集、销项发票信息数据集,以及银行贷款年利率与不同信誉等级下的客户流失率的统计数据集。其中,企业信息数据集包括123 家企业的企业代号、企业名称、企业信用评级以及企业历史违约情况。企业进项发票数据集、销项发票数据集分别包含123 家企业采购及销售时所开发票的记录,记录中包括发票号码、开票日期、销方单位代号、购方单位代号、金额、税额、价税合计和发票状态。银行贷款年利率与不同信誉等级下的客户流失率的统计数据集包括贷款年利率对应于不同信誉评级的企业的客户流失率的统计数据。
4.2 计算原始指标
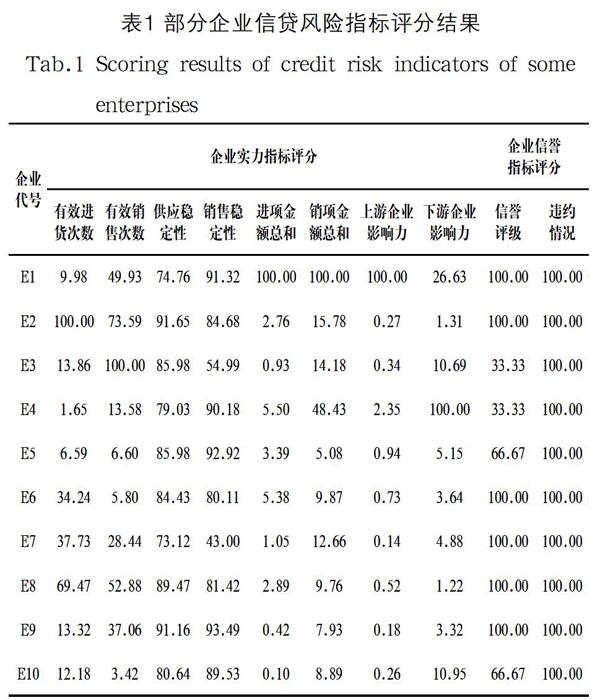
对企业信誉及实力的10 个原始评价指标进行计算。同时,为了消除不同指标之间量纲的影响,对每个评价指标进行极大值标准化。部分企业信贷风险指标评分结果如表1所示。
4.3 基于降维后的指标对企业进行不同风险等级的聚类实验及结果分析
基于降维后的三个指标对123 家企业进行聚类,值为5。不同风险等级企业聚类结果如图2所示。
123 家企业根据企业交易规模指标、企业信誉指标、企业盈利能力指标聚成五类,依次为:低风险企业共1 家,较低风险企业共7 家,中等风险企业共86 家,较高风险企业共2 家,高风险企业共27 家。通过比对对应企业原始10 个指标,其聚类结果与实际情况基本一致。
4.4 企业信贷违约率计算的实验及结果分析
通过Fisher线性判别,根据式(4),对企业违约情况进行预测,准确率达77.2%。进而计算企业违约概率与企业不违约概率,部分计算结果如表2所示。
4.5 银行信贷策略的实验及结果分析
通过对贷款额度模型式(5)及贷款利率模型式(8)的求解,得到对五类风险等级企业的贷款策略,完整贷款策略如表3所示。
其中,a为银行放贷的总额度。对于风险较低的企业类别,可以获得较大的贷款额度,同时享受较低的贷款利率;而对于风险较高的企业,则在获得较低贷款额度的同时,需
要支付较高的贷款利率。这与实际情况相符,亦证明了模型的可行性与有效性。
5 结论(Conclusion)
本研究通过对123 家中小微企业的进项、销项发票数据进行研究,得出评价其风险等级的10 个原始指标。通过PCA降维、K-means聚类等机器学习常用技术,将123 家企业划分成五类风险等级,并根据有效进货次数、有效销售次数和企业信誉等指标进行Fisher线性判别预测,计算得出不同风险等级下,企业的平均违约率及贷款额度。继而根据银行年利率与客户流失率的统计数据信息,构建银行贷款收入的非线性优化模型。通过对非线性优化模型的求解,得出银行对不同风险等级下企业的贷款利率。
参考文献(References)
[1] 梁钰.新冠肺炎疫情下小微企业融资支持举措效果评估及改进建议——基于湖南岳阳的调查[J].金融经济,2020(10):58-61,72.
[2] 钟成林,胡雪萍.中小民营企业融资困境的形成机理及政策支持体系研究——基于群体性与个体性金融声誉交互作用视角[J].社会科学,2019(05):50-58.
[3] 郑建华,黄灏然,李晓龙.基于大数据小微企业信用评级模型研究[J].技术经济与管理研究,2020(07):22-26.
[4] 郝晓露,高巍.商业银行贷款分配及盈利最大化的计量探析[J].湖北经济学院学报(人文社会科学版),2019,16(09):48-51.
[5] 王薛.农村信用社农户贷款风险评价与控制研究[D].保定:华北电力大学,2007.
[6] 房斌.P银行小微企业信贷风险评价体系研究[D].西安:西安石油大学,2020.
[7] 陈琳,季凌.基于数据挖掘的中小企业客户信用评级模型的设计与实现[J].海峡科技与产业,2019(01):176-178.
[8] 赵蔷.主成分分析方法综述[J].软件工程,2016,19(06):1-3.
[9] TANG J L, ZHANG Z G, WANG D, et al. Research on weeds identification based on K-means feature learning[J]. Soft Computing, 2018, 22(22):7649-7658.
[10] 徐晓萍,马文杰.非上市中小企业贷款违约率的定量分析——基于判别分析法和决策树模型的分析[J].金融研究,2011(03):111-120.
[11] 迟国泰,龚玲玲.商户小额贷款决策模型[J].技术经济,2016,35(04):98-103.
[12] 牟太勇.基于信用风险评估的商业银行贷款定价研究[D].成都:电子科技大学,2007.
作者简介:
顾一凡(2000-),男,本科生.研究领域:机器学习.
黄莉媛(1999-),女,本科生.研究领域:金融学.
林晨欣(2000-),女,本科生.研究领域:金融生态.
曹春萍(1968-),女,硕士,副教授.研究领域:智能数据处理,个性化服务.
