基于热阻抗模型的三相逆变器功率器件结温监测方法

张思慧，赵 蕤，闫 帅，徐 强，宋文胜

（西南交通大学电气工程学院，成都 611756）

近十年我国高速铁路里程增长迅速，截至2020 年底，高速铁路里程已达3.9 万公里，超过世界高速铁路总里程的65%[1]。大功率牵引系统是高速动车组的“心脏”，牵引变流器是牵引传动系统的核心部件，其可靠性由其拓扑结构可靠性和功率器件本身可靠性共同决定[2]。调查显示，功率器件是失效概率最大的组件，且导致功率器件失效的主要因素有温度、湿度、振动冲击以及污染物等，其中约55%的功率器件失效由温度因素诱发[3]，因此，功率器件结温的精准监测是其寿命预测、健康管理与可靠性评估的基础[4]。

现有功率器件结温监测方法主要分为4 大类，分别为物理接触式测量法[5]、光学非接触测量法[6-7]、热敏电参数提取法[8]和热阻抗模型预测法[9]。其中，物理接触式测量法是将热敏电阻或热电偶等测温元件放在待测功率器件内部，根据各种测温元件自身参数变化来获取功率器件内部的温度信息，其侵入性强，准确性较低[10]；光学非接触测量法主要利用光温耦合效应的表征参数，借助红外热成像仪等仪器，测量IGBT 模块的结温，如文献[6]采用红外热成像仪开展电力电子功率器件的结温监测，但该方法需要破坏待测器件封装，且对红外热成像仪的采样率要求较高；热敏电参数提取法是一种通过在线提取IGBT 模块外部电气特征参数估算结温的方法，其原理是提取功率器件外部电气特征参数与器件内部结温存在的对应关系，但在获取映射关系的过程中由于负载电流的影响，都存在不同程度的自热现象，使提取的映射关系产生估算误差[4]；热阻抗模型预测法主要是根据器件损耗以及热阻抗模型，通过仿真计算等方式推导出器件结温，该方法在大容量变换器的散热系统评估方面应用广泛[11]，准确性和实用性较高，如文献[12]提出了一种考虑多热源耦合影响的变流器功率模块结温评估改进模型，利用有限元方法分析了IGBT 模块内多芯片的结温分布和稳态热耦合影响，但其模型较为复杂，所需的参数较多；文献[13]提出了一种利用高斯赛德尔迭代法对逆变器中IGBT 模块结温进行计算的方法，该方法的计算速度较快，易满足实际应用要求，但精度较低。

本文基于SVPWM 的两电平三相逆变器，利用热阻抗模型预测法对IGBT 模块的结温进行监测，分析并搭建IGBT 模块的损耗模型和热网络模型，分析导通电流和温度对导通压降、开通损耗、关断损耗的影响，并拟合其关系式，在此基础上分别讨论有、无结温修正情况下的结温计算结果，研究结温对计算模型的影响，并与PLECS 热仿真结果进行对比。最后开展小功率两电平三相逆变器结温监测实验测试，利用热敏电阻法测量IGBT 模块的结温，并与计算结果以及仿真结果进行分析比较，验证所提模型的准确性和可行性。

1 三相逆变器的IGBT 模块损耗计算

1.1 IGBT 模块的损耗计算原理

IGBT 模块的热量主要源于芯片产生的损耗，因此分析IGBT 芯片和反并联续流二极管FWD（freewheeling diode）的损耗是结温计算的第一步。由文献[14]可知，IGBT 模块的损耗主要由IGBT 损耗PI和FWD 损耗PD组成，其中：PI一般包括IGBT 的导通损耗PIc、开通损耗PIon和关断损耗PIoff，其中开通损耗和关断损耗合称开关损耗PIs；PD一般包括FWD 导通损耗PDc和反向恢复损耗PDs。

1）IGBT 导通损耗

由于IGBT 导通状态下会有一定的饱和压降，且有内部通态电阻，因此IGBT 导通时的损耗表示为

式中：VCE为IGBT 完全导通时集射极两端的压降；IC为流过IGBT 的电流瞬时值；rI为IGBT 导通时的内部通态电阻。

2）IGBT 开关损耗

由于IGBT 开关时其电压、电流波形会有一段时间的重叠，所以会产生开关损耗。IGBT 的数据手册中提供额定运行条件下的开通损耗和关断损耗，因此只须利用提供的数据计算，即可得出IGBT 每次开关产生的开关损耗为

式中：Ts为IGBT 模块的开关周期；Eon和Eoff分别为额定条件下每脉冲的开通和关断损耗能量；Udc为直流侧电压；UN-IGBT和IN-IGBT分别为IGBT 模块的额定电压和额定电流。

3）FWD 导通损耗

FWD 也有导通损耗，可表示为

式中：VF为FWD 导通时两端的压降；ID为流过FWD 的电流瞬时值；rD为FWD 的通态电阻。

4）FWD 反向恢复损耗

IGBT 模块中的反并联二极管一般都具有快恢复特性，其开通损耗远小于反向恢复损耗，因此可忽略不计[15]，其反向恢复损耗也称为关断损耗，在FWD 关断过程中，其反向阻断能力的恢复需要一段时间，期间FWD 的两端电压和电流有重叠，因此会产生反向恢复损耗。所以，FWD 每次开关产生的开关损耗为

式中：Eref为FWD 额定运行条件下的反向恢复损耗能量；UN-D和IN-D分别IGBT 反并联二极管的额定电压和额定电流。

1.2 SVPWM 下逆变器中IGBT 模块的损耗计算

由于本文研究的是SVPWM 下逆变器中IGBT模块的损耗与结温，流经IGBT 和FWD 的电流和占空比会不断变化，IGBT 的导通压降也会随着电流和温度的变化而改变，因此需要根据三相逆变器的结构、调制方法和IGBT 的模型参数，建立具体的损耗计算模型。

两电平三相逆变电路如图1 所示，根据SVPWM 的调制原理，可以通过不同扇区内2 个相邻电压矢量的作用时间得到不同扇区的空间电压矢量切换点tcm1、tcm2、tcm3。以逆变器a 相桥臂的上管IGBT模块（T1和D1）为例，该管在一个开关周期内的导通时间ton为

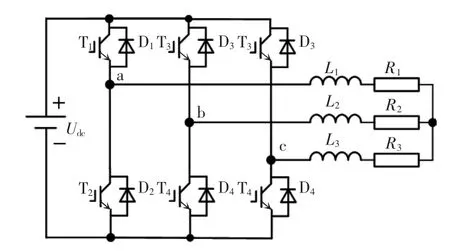
图1 两电平三相逆变器电路原理Fig.1 Schematic for the circuit of two-level three-phase inverter

进而可以得到a 相桥臂上管IGBT 的导通占空比D 为

以Infineon-FP75R12KT4 型号的IGBT 数据手册为例，其IGBT 模块参数曲线如图2 所示。

导通压降VCE与导通电流IC和结温TjI的关系曲线如图2（a）所示，通过拟合曲线的方式可以得到VCE与IC的关系以及VCE与TjI的关系，分别表示为

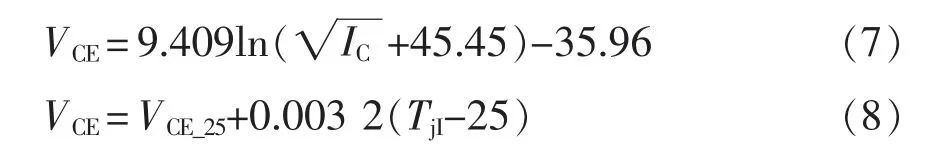
式中，VCE_25为25 ℃下的导通压降。

根据图2（b）可拟合出IGBT 一次开通和关断过程的消耗能量Eon和Eoff与IC的关系，分别为

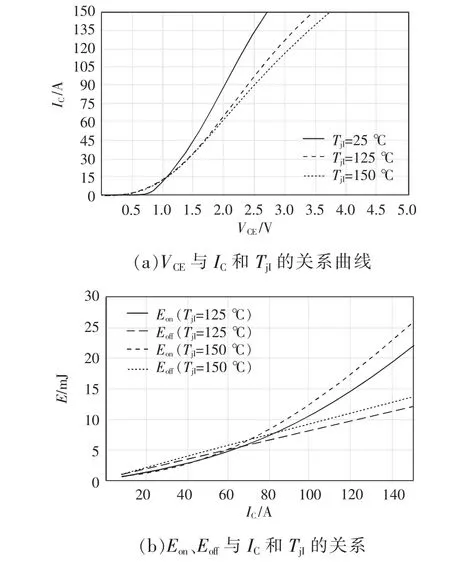
图2 Infineon-FP75R12KT4 型IGBT 模块参数曲线Fig.2 Parameter curves of Infineon-FP75R12KT4-type IGBT module

Eon和Eoff与TjI的关系分别为

式中：Eon_125为125 ℃下IGBT 开通一次的损耗能量；Eoff_125为125 ℃下IGBT 关断一次的损耗能量。

同理，可以得到二极管相应的参数，在此基础上，可以得到SVPWM 下两电平三相逆变器中功率器件的损耗计算模型。

一个开关周期内IGBT 的导通损耗为

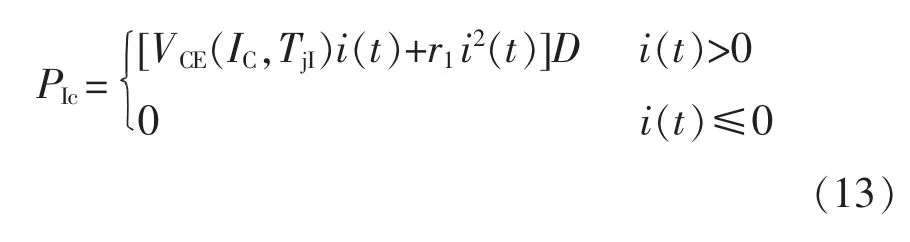
式中，i（t）为流过IGBT 的瞬态电流。

每次开关产生的IGBT 开关损耗为

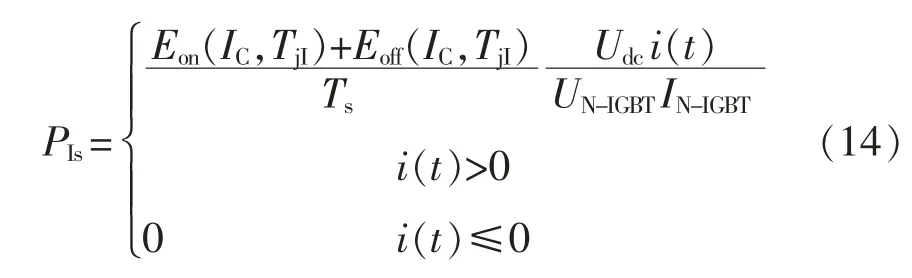
一个开关周期内FWD 的导通损耗为

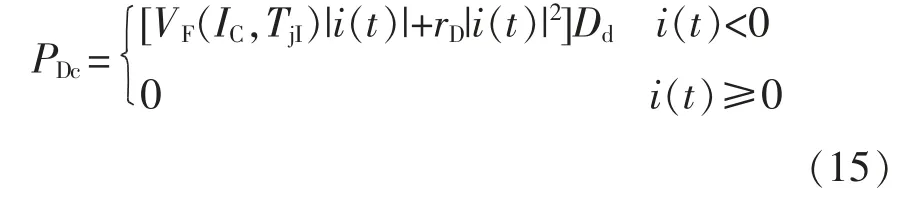
式中，Dd为FWD 的导通占空比。

每次开关产生的FWD 反向恢复损耗为

2 基于热网阻抗模型的IGBT 模块结温估算

Cauer 热网络模型和Foster 热网络模型是对IGBT 模块实际传热过程的集中等效。Cauer 热网络模型可以描述IGBT 模块各层的热阻和热容，但其参数较难获得；Foster 热网络模型与实际封装内各层不存在对应关系，但其参数的获取和计算都相对较容易，且2 种模型是相互等效的[16]。因此，为了参数提取的方便，本文选用Foster 热网络构建IGBT模块的等效传热模型。

由于IGBT 模块在工作期间会产生大量的热量，导致IGBT 模块的结温升高，因此实际应用中，会在IGBT 模块的基板下加装散热器，增加IGBT模块的散热面积，减缓IGBT 模块结温的上升。因此IGBT 模块的等效传热模型需要考虑散热器的热阻抗，等效传热模型如图3 所示。

图3 中：ZIjc、ZDjc为IGBT芯片和FWD芯片到铜基板的热阻抗；ZIch、ZDch为IGBT 和FWD 铜基板到散热器的热阻抗；Zh为散热器的等效热阻抗；Ta为环境温度；RI1、RI2、RI3、RI4分别为IGBT 从结到壳的各层材料Foster 型等效热阻；CI1、CI2、CI3、CI4分别为IGBT 从结到壳的各层材料Foster 型等效热容；RD1、RD2、RD3、RD4分别为二极管从结到壳的各层材料Foster型等效热阻；CD1、CD2、CD3、CD4分别为二极管从结到壳的各层材料Foster 型等效热容；RI5、CI5分别为IGBT 从壳到散热器的Foster 型等效热阻和热容；RD5、CD5分别为二极管从壳到散热器的Foster型等效热阻和热容；R6、C6分别为散热器到外界环境的Foster 型等效热阻和热容。这些参数均可从IGBT 模块的数据手册中获取。

图3 IGBT 模块等效传热模型Fig.3 Equivalent thermal transfer model of IGBT module

基于两电平三相逆变器中的IGBT 模块等效传热模型，IGBT 的结温TjI与FWD 的结温TjD可分别表示为

式中，Δt=1/（2f），f 为逆变器输出电压的基波频率。

3 理论计算结果与PLECS 仿真验证

针对SVPWM 下三相逆变器中的IGBT 模块进行结温的仿真，分别使用Matlab/Simulink 仿真软件和PLECS 仿真软件进行分析。根据上述结温计算的模型，在Matlab/Simulink 仿真平台搭建三相逆变器中IGBT 模块无结温反馈和带结温反馈2 种结温计算模型，同时在PLECS 仿真软件中搭建相同的三相逆变器电路，并使用其自带的热仿真功能进行IGBT 结温仿真。

图4 给出了IGBT 模块的结温计算流程，其中图4（a）为无结温反馈的计算流程，图4（b）为带结温反馈的计算流程。

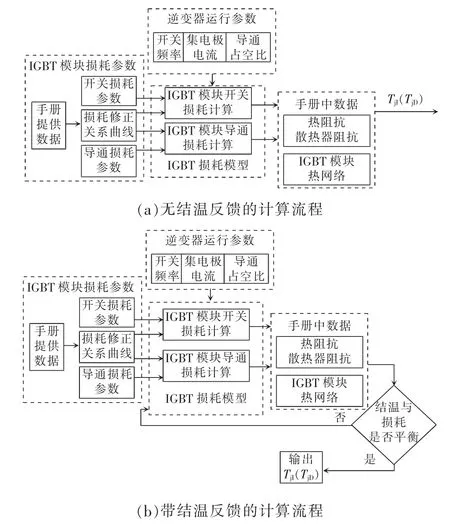
图4 IGBT 模块结温计算流程Fig.4 Flow chart of junction temperature calculation of IGBT module

以Infineon-FP75R12KT4 型号的IGBT 模块为例，搭建基于SVPWM 的三相逆变器仿真模型，根据逆变器仿真结果和IGBT 模块数据手册得出所需参数，将参数代入以上2 种Matlab 计算模型并运行，得到IGBT 的结温变化曲线。同时，为验证结温计算模型的准确性，利用PLECS 软件对IGBT的结温进行仿真分析，在PLECS 仿真软件库中加入该型号IGBT 的热模型文件，在相同的电路和参数下进行热仿真，得到IGBT 的结温变化曲线。计算和仿真所用的初始温度均为实测室温24 ℃，2种计算方法和PLECS 仿真下的IGBT 结温变化曲线如图5 所示，稳定后2 种计算方法和PLECS 仿真下的IGBT 结温细节曲线如图6 所示，其数据对照如表1 所示。

表1 计算结果与仿真结果的数据对比Tab.1 Comparison of data between calculation and simulation results ℃

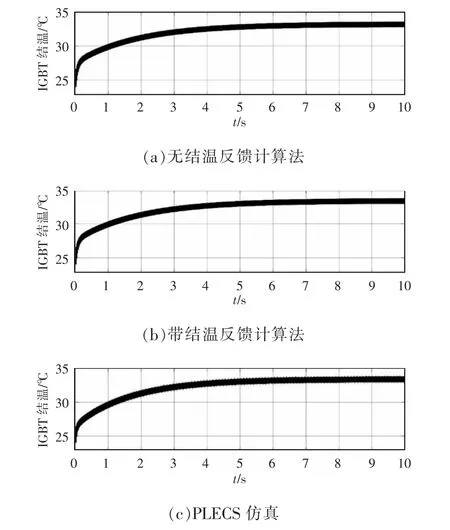
图5 2 种计算方法和PLECS 仿真下的IGBT 结温变化曲线Fig.5 Junction temperature curve of IGBT under two calculation methods and PLECS simulation

图6 稳定后2 种计算方法和PLECS 仿真下的IGBT结温细节曲线Fig.6 Detailed curve of IGBT junction temperature under two calculation methods and PLECS simulation after stabilization

对仿真结果进行分析可知，IGBT 结温的波动频率与逆变器基波频率相同，并且相比于无结温反馈的计算方法，带结温反馈的计算方法结温波动幅值更大，因为常规方法不能有效反映损耗的实时变化，因此带结温反馈的方法更为精确，更接近于PLECS 热仿真结果。同时，也验证了热阻抗模型法的正确性和可行性。

4 实验结果分析和验证

采用（Infineon-FP75R12KT4）1 200 V/75 A 的IGBT 模块搭建两电平三相逆变器实验电路，通过DSPACE 平台和Matlab/Simulink 仿真软件联合控制，实现对逆变器的调制信号输入和结温信号采集，实验平台如图7 所示，实验主要参数如表2 所示。IGBT 内热敏电阻阻值与温度的关系曲线如图8所示，可通过实时反馈热敏电阻的阻值对应得到IGBT 结温，此方法属于物理接触式测量法。

图7 三相逆变器结温监测实验平台Fig.7 Experimental platform for junction temperature monitoring of three-phase inverter

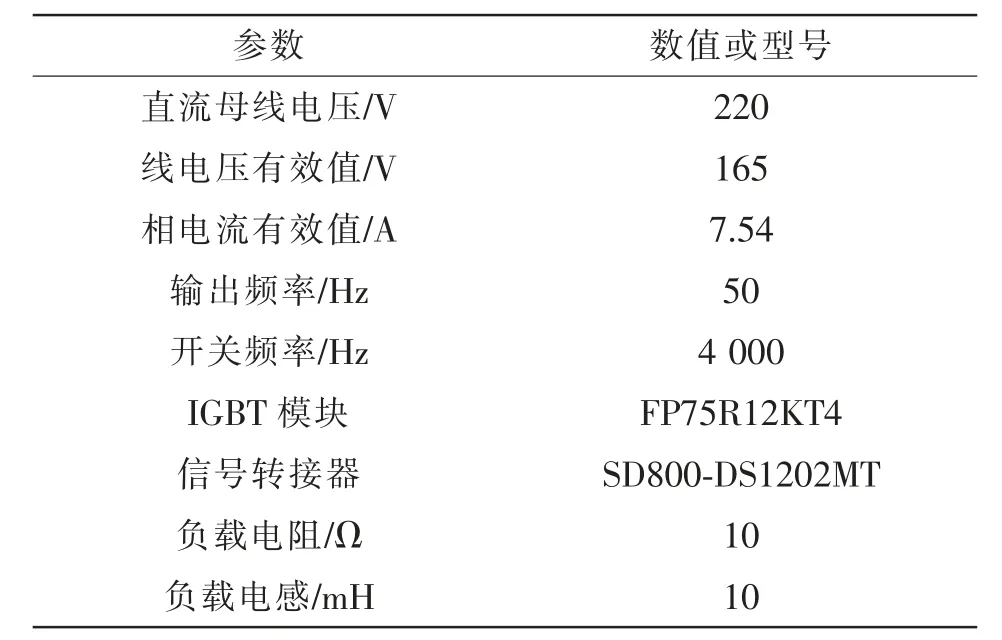
表2 实验平台的主要参数Tab.2 Main parameters of experimental platform

图8 IGBT 热敏电阻与温度的关系曲线Fig.8 Curve of relationship between IGBT thermistor and temperature

图9 是逆变器第一桥臂上管IGBT 模块结温变化曲线的理论计算结果、仿真结果和实验结果，环境温度为24 ℃，由于小功率实验采用的是热敏电阻法间接得到IGBT 结温，受限于传感器的采样频率，无法测得每个开关周期内IGBT 结温的波动过程，只能得到其平均结温，所以实验所得的结温曲线较为平滑，无波动过程。由结果可明显看出实验所得的IGBT 结温变化趋势与理论计算、PLECS 仿真结果基本相同。表3 给出了理论计算、PLECS 仿真和小功率实验的对比结果。

图9 IGBT 模块的结温变化结果Fig.9 Results of changes in junction temperature of IGBT module

由表3 可知，本文采用的带结温修正的热阻抗模型法计算值和测量值较为吻合，误差为1.827%，基本证实了本文两电平三相逆变器损耗计算的准确性，能满足工程散热设计的要求。而无结温修正的热阻抗模型法未考虑结温变化对IGBT 模块参数的影响，恒定采用25 ℃下的器件参数，因此其IGBT模块结温计算值偏小，误差率也较高，在3%左右。

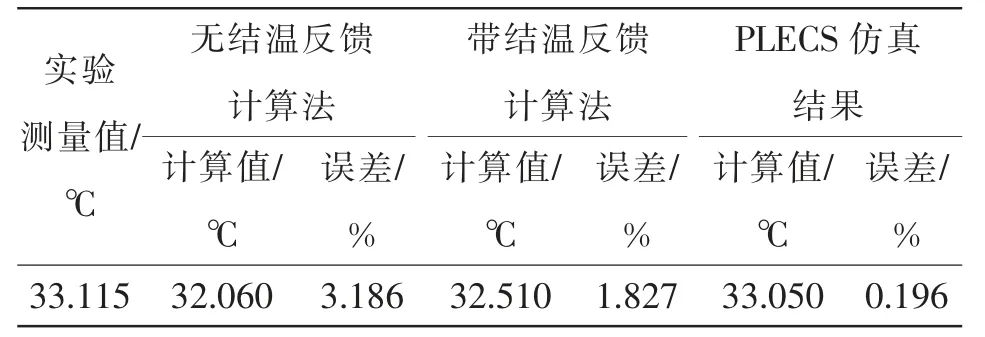
表3 理论计算、仿真与实验结果对比Tab.3 Comparison among theoretical calculation,simulation and experimental results

5 结语

针对SVPWM 下两电平三相逆变器，研究IGBT模块损耗计算和基于热阻抗网络模型的结温计算方法，本文通过引入电流和温度对IGBT 模块导通压降的影响，以及实际工作中的电压、电流和温度对IGBT 模块开关损耗的影响，提高了逆变器中IGBT 结温计算的精度。通过PLECS 热仿真和小功率实验对结温理论计算方法进行了验证研究，仿真和实验结果表明，带结温反馈的结温计算模型更为精确，计算误差在2%以内，因此该方法更适用于逆变器中IGBT 模块结温的准确计算，为功率器件主动热管理和寿命预测的研究奠定了基础。