几种简单的预测类数学模型及其在企业生产中的应用分析

时岩 韩登利 胡守华

莱芜职业技术学院机电工程系 山东 莱芜 271100

引言

在信息化、市场化、国际化日新月异的今天，客户的个性化、多样化需求已然成为企业生产的核心，特别对于大型装备制造企业来说，严格按照客户的订单安排生产，成为主要的生产方式。如果能够对订单数量进行准确预测，企业便可以快速地根据订单情况的预期及时调整企业的生产经营活动，包括产能分配、库存优化，从而最大限度压缩成本，提高企业利润。因此，对未来客户订单的精确预测对于大型装备制造企业及时把握市场商机，提高企业竞争力有重要意义。而数学建模正是解决预测问题的有效方法。下面我们将简要介绍几种简单易操作的预测类模型的建模原理和一般步骤，并结合某公司的实际数据进行订单预测。

1 数据拟合模型的一般原理

在企业的生产实践和科学研究实验中，为了认识事物的内在规律，准确把握其本质属性，人们需要研究某些变量之间的函数关系，而这些未知函数关系往往隐藏在大量的数据中。因此，解决问题的关键是如何从调研观测或生产销售中得到的一组统计或观测数据中，找到变量之间相对准确的函数关系。解决该种问题的有效方法之一就是数据拟合[1]。

数据拟合是指把已知数据看作平面上n个点，其中互不相同，寻求合适的函数，使在某种准则下与所有数据点最为接近，即曲线拟合得最好。

2 多项式数据拟合的一般步骤及其应用

2.1 多项式拟合的一般步骤

根据前述知识可以总结得到建立多项式拟合模型的一般步骤：第一，画出已知数据的散点图，确定拟合多项式的次数m；第二，计算，建立并求解多项式系数方程组，求得系数；第三，得到拟合多项式函数。第四，拟合模型的检验与应用。

实际应用中不用进行复杂的数学计算，可以借助MATLAB软件来实现拟合，通常采用polyfit，polyval等命令编写程序完成拟合工作，或者采用Basic-fitting拟合工具箱进行拟合，可以方便快捷得到结果。

2.2 多项式拟合应用

案例：A公司是位于山东中部的一家大型装备制造企业，近几年公司的经营发展蒸蒸日上，现有公司最近两年共8个季度的某大型成套矿用设备订单数据，如表1所示。该公司希望通过对此部分订单数据的分析，建立数学模型，对今后两个季度的产品订单量进行预测，以期能够及时制订或调整优化生产计划[2]。

表1 A公司某成套矿用设备订单数据

借助MATLAB软件中的plot函数画出已知数据散点图（见图1），根据图形特点确定拟合多项式的次数 。

图1 历史订单量散点图

采用polyfit，polyval命令编写程序得拟合系数

根据上述模型计算得各季度的模型预测值及实际订单数值对照如下表。

表2 多项式拟合模型预测结果

可知，后续两个季度的订单预测量分别约为48套、50套，相应的误差指标也比较小。

3 非多项式拟合模型及其应用

3.1 一般形式的非多项式拟合模型

多项式拟合比较容易实现，但有时我们需要对非多项式的历史数据进行拟合，并预测未来数据。Malthus拟合和Logistic拟合是非常著名的非多项式拟合模型，但是其可以实现的预测场景也比较有限，这里不再赘述。对于自定义函数来进行拟合的情形，下面基于MATLAB的相关功能介绍一般形式的非多项式拟合模型。

与多项式拟合模型类似，建立非多项式拟合模型的步骤为：

检验与预测。

实际计算一般借助MATLAB软件中的lsqcurvefit，nlinfit等命令编写程序完成拟合工作。

3.2 非多项式拟合模型的应用

在前述案例中，也可以根据实际需要建立非多项式拟合模型。

通过对图1所呈现的规律分析，我们认为该图形兼具有线性函数和对数函数的特征。设x表示时间（季度），y表示订单量，a，b，c为需要拟合的模型参数，所求模型为

借助MATLAB中的nlinfit命令编写程序，运行得拟合结果

得到非多项式拟合函数

模型的检验与预测。根据上述模型计算得各季度的预测值及实际订单数值如表3。

表3 非多项式模型预测结果

可以看出，后续两个季度的订单预测量分别约为50套、52套，相应的误差指标较前一模型稍高。

4 灰色预测模型

对于小数据预测问题，邓聚龙教授提出了灰色预测理论。通过对部分已知信息的提取和开发，能够进行较为精确地预测。具有所需样本少、运算简便和易于检验等特点。这种利用较少的或不确切的表示灰色系统行为特征的原始数据序列作生成变换后建立的，描述灰色系统内部事物连续变化过程的模型，称为灰色预测模型，一般简称为GM模型。

4.1 构建灰色预测GM（1,1）模型的一般方法

累加生成新序列：

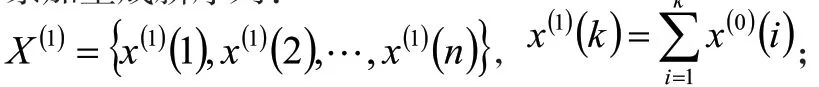
求解该微分方程得预测模型可由下式表示：

实际应用中，模型的求解通常也运用MATLAB编程得到相应预测结果。

4.2 灰色预测GM（1,1）模型的应用

对于前述案例建立订单量数据时间序列

求得级比

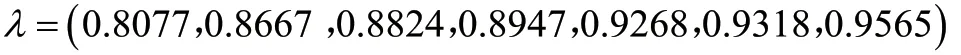
在可容范围（0.8007,1.2488）内，可以建立GM（1,1）模型。

累加生成新序列 ；

运用MATLAB编程可快速得到相应预测结果如表4：

表4 灰色模型预测结果

续表

在此模型下，后续两个季度的订单预测量分别约为51套、54套，误差指标较前面模型明显更大。

5 模型的比较

本文对于同一案例运用三种不同方法进行了建模预测，从求解的结果对比来看，多项式建模的结果相对来说精确度更高，误差更小一些，但这仅是针对本文案例的数据的结果。实际应用中其他的数据可能是另一种情形，所以不能据此断定多项式模型永远是最好的，需要具体问题具体分析。另外，预测类问题多数情况下是基于已有历史数据的基础上的，通过前期数据推断其既有的规律，这类估计方法一般需要有大量的已有数据的支持，当已有的原始数据比较少时，问题内部隐藏的规律就不能很好地反映出来，由此会带来较大的预测误差。预测类建模的方法还有很多，比如微分方程模型、插值模型、马尔科夫链模型、时间序列模型、神经元网络模型等，读者可参阅相应书籍资料。