新制标准铂电阻温度计退火特性理论模型及验证

于 帆, 孙建平, 李 婷, 朱天梦, 王成科

(1. 北京科技大学 能源与环境工程学院,北京 100083；2. 中国计量科学研究院,北京 100029；3. 中国计量大学,浙江 杭州 310018)

1 引 言

标准铂电阻温度计(standard platinum resistance thermometer，SPRT)是ITS-90国际温标定义内插仪器之一,其稳定性是当前温标发展的瓶颈。稳定性与多种影响因素有关,如铂丝的纯度、内部残余应力及氧化等,其中内部残余应力的影响尤为关键。内部残余应力主要是由铂丝在制造过程中的机械冷拔,温度计传感元件绕制过程中的机械变形,以及温度计在使用过程中的机械震动或温度的剧烈变化引起的；内部残余应力可通过在铂电阻温度计对应的上限温度进行退火处理来减小或消除。SPRT退火主要分为2种情况,即新制作的铂电阻温度计在上限温度的长时间首次退火,以及铂电阻温度计在使用中的退火[1～4]。

SPRT采用的高纯铂丝直径通常为0.07 mm,名义电阻为25 Ω,主要通过冷拔方式生产。从微观上看,冷拔生产工艺会造成大量的晶格位错、晶界等高密度的晶体缺陷,以致产生大量内部残余应力。其中位错一般在经历高温退火后会消失或变小；另外,SPRT元件在制作过程中涉及绕制线圈及接点焊接等工艺,不可避免也会造成不稳定的内部应力增加。因此,热处理工艺是新制SPRT获得高稳定性的关键。当前，我国计量检定规程JJG 160—2007[5],美国NIST的研究[6],ITS-90补充材料建议[7],欧盟EUROMET-K3的国际比对[8]等对于SPRT稳定性的考核、热处理时间和温度的要求都不尽相同,退火过程中温度计电阻值随退火时间的变化规律几乎完全依靠实验测定,亟需理论模型公式的指导。

本文应用再结晶动力学中的相关理论，研究标准铂电阻温度计整个退火过程中的电阻变化规律,对水三相点电阻值和对应温度值随时间的变化趋势建立理论模型或数学计算公式,以指导和优化SPRT的退火热处理工艺。

2 理论模型

标准铂电阻温度计稳定性退火上限温度为 660 ℃,在此温度下退火时铂丝要经历回复、再结晶及晶粒长大3个过程。高温退火时,一般回复时间很短,之后就会进入再结晶阶段,直至晶粒长大到一个稳定的尺寸。Avrami方程[9]是描述材料再结晶动力学过程的经典公式：

X=1-exp(-Btk)

(1)

式中：X为再结晶体积分数；t为时间；B和k为与再结晶具体过程有关的参数,分别称作再结晶参数和再结晶指数。

随着再结晶体积分数的增大,材料内部缺陷体积分数逐渐减小,而随着内部缺陷如位错和晶界等的减少,材料的电阻也会随之变小直至趋于稳定,因此可以将再结晶体积分数与材料电阻的变化关联起来。基于对多支标准铂电阻温度计大量退火实验数据的观察、整理及综合分析,发现在水三相点上SPRT电阻值随退火时间的变化趋势具有指数函数的特点。因此本文认为不仅仅局限于再结晶阶段而是在整个退火过程中,标准铂电阻温度计在经历首次退火处理时,水三相点电阻值随时间的变化趋势用函数形式都可以近似用Avrami方程来描述,故本文尝试提出：

R(t)=Rm[exp(-Btk)-1]+R(0)

(2)

式中：R(t)为经历退火时间t后的水三相点电阻值；R(0)为初始电阻值；Rm为电阻变化幅值,当t→∞时,R=R(0)-Rm,此时R为SPRT充分退火后(理想情况下)水三相点电阻值；B和k为与铂丝退火具体过程有关的参数和指数。

引入电阻变化ΔR=R(t)-R(0),则式(2)可以整理成：

ΔR=Rm[exp(-Btk)-1]

(3)

由铂电阻的温度系数可得到与电阻变化ΔR相对应的温度变化值ΔT：

ΔT=Tm[exp(-Btk)-1]

(4)

式中：Tm是与Rm对应的温度变化幅值,即t→∞时,ΔT=-Tm。定义无量纲温度变化或无量纲电阻变化为ΔT*=ΔT/Tm=ΔR*=ΔR/Rm,则：

ΔT*=exp(-Btk)-1

(5)

或者：

ΔT*+1=exp(-Btk)

(6)

对式(5)、式(6)两端取2次对数可得到：

ln[-ln(ΔT*+1)]=lnB+klnt

(7)

可见,双对数无量纲温度或电阻变量ln[-ln(ΔT*+1)]与对数时间lnt成线性关系,直线的斜率为k,截距为lnB。式(3)、式(4)、式(5)及式(7)即为SPRT首次退火处理过程中水三相点电阻值变化或对应温度值变化(稳定性)的理论模型。

由于模型中的3个待定参数Tm(或Rm)、B和k是线性无关的,依据参数估计理论[10],按照理论模型公式对实验测量数据进行基于最小二乘法的函数拟合及参数计算,就可以同时获得公式中的3个待定参数,即温度变化幅值Tm(或电阻变化幅值Rm)、退火参数B和退火指数k。

若引入退火特征时间tR,式(5)也可以表示为：

ΔT*=exp[-(t/tR)k]-1

(8)

其中退火特征时间tR与退火参数B和退火指数k的关系为：

tR=(1/B)1/k

(9)

退火特征时间tR的物理意义为无量纲温度变化ΔT*为-0.632 1时的退火时间。

3 实验与理论比较

检查退火后SPRT电阻在水三相点的变化是评价其稳定性最常用且有效的方法。本文实验数据来自于中国计量科学研究院新制的15支SPRT在660 ℃退火后水三相点下电阻的测量结果。温度计由直径为0.07 mm的高纯铂丝制成,名义电阻为25 Ω,均达到了JJG 160—2007规定工作基准的技术要求。实验数据按照建立的理论模型进行了基于最小二乘法拟合的多参数计算,结果见图1～图3。

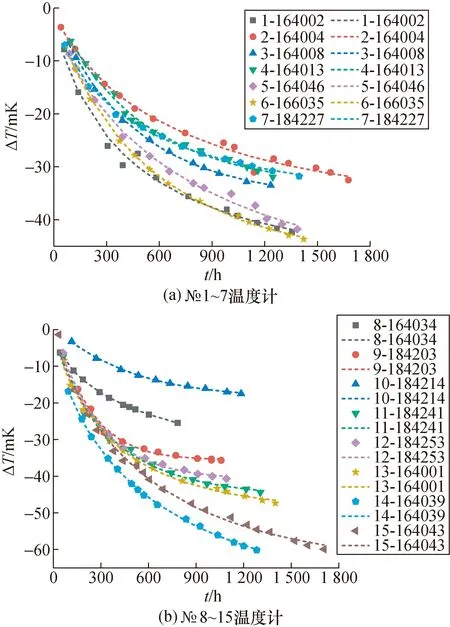
图1 水三相点下温度变化与退火时间结果Fig.1 Experimental and theoretical results of the temperature change and annealing time at water triple point

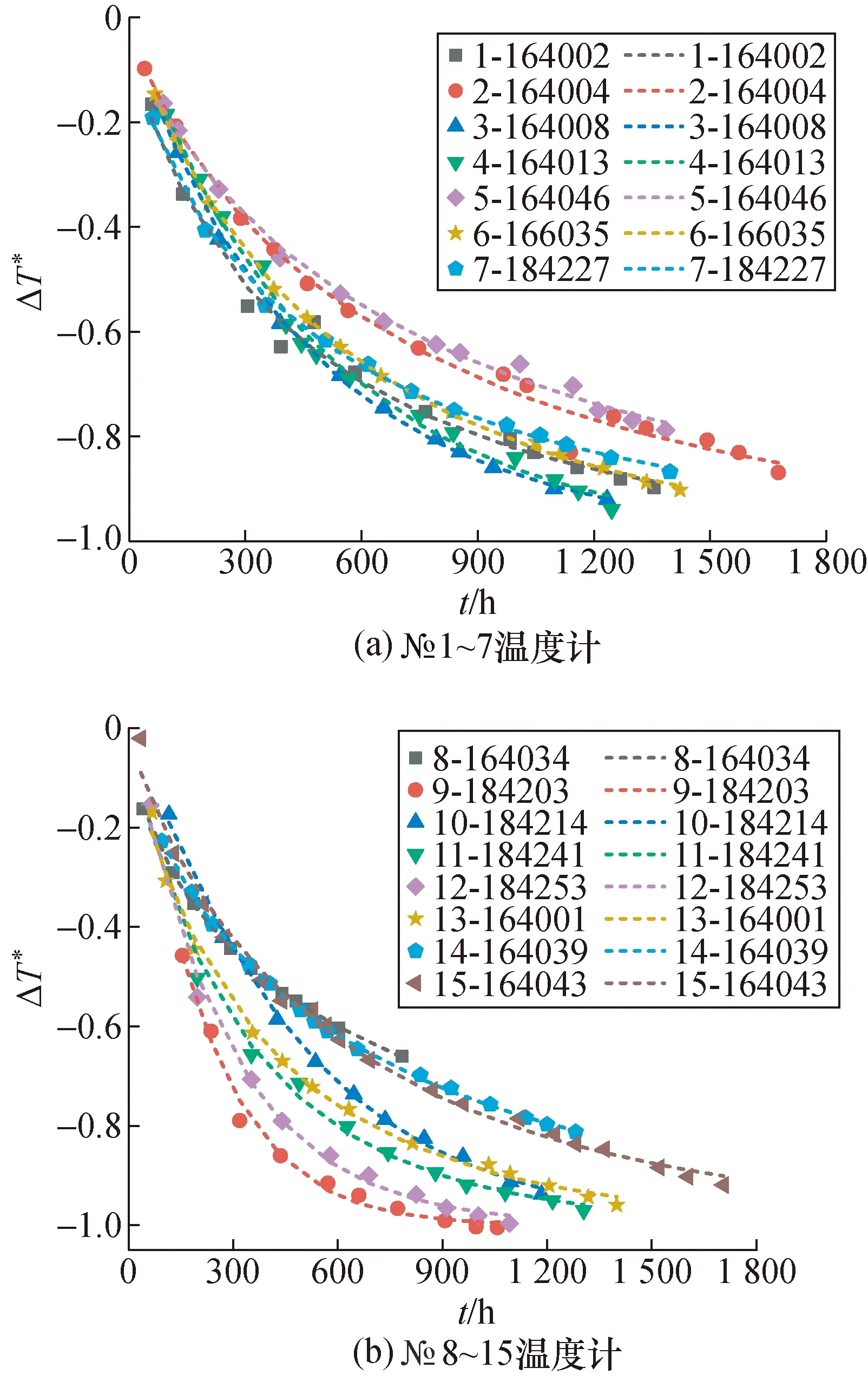
图2 水三相点下无量纲温度变化与退火时间结果Fig.2 Experimental and theoretical results of the dimensionlesstemperature change and annealing time at water triple point

图3 水三相点下双对数无量纲温度变化与退火对数时间结果Fig.3 Experimental and theoretical results ofdouble logarithmic dimensionless temperature change and annealing logarithmic time at the water triple point

图中散点为实验值,连线为理论计算值。由图可知,15支标准铂电阻温度计实验数据与理论模型除个别点外总体吻合较好,双对数无量纲电阻值变化与对数时间呈现出明显的线性关系,且线性拟合度良好,表明建立的整体退火过程中铂电阻温度计在水三相点电阻值及对应的温度值随时间变化的理论模型是合适的,可以用来表示或描述温度计的退火特性。

表1为15支标准铂电阻温度计退火后水三相点下电阻值变化幅值Rm对应的温度变化幅值Tm、退火参数B和退火指数k以及退火特征时间tR。

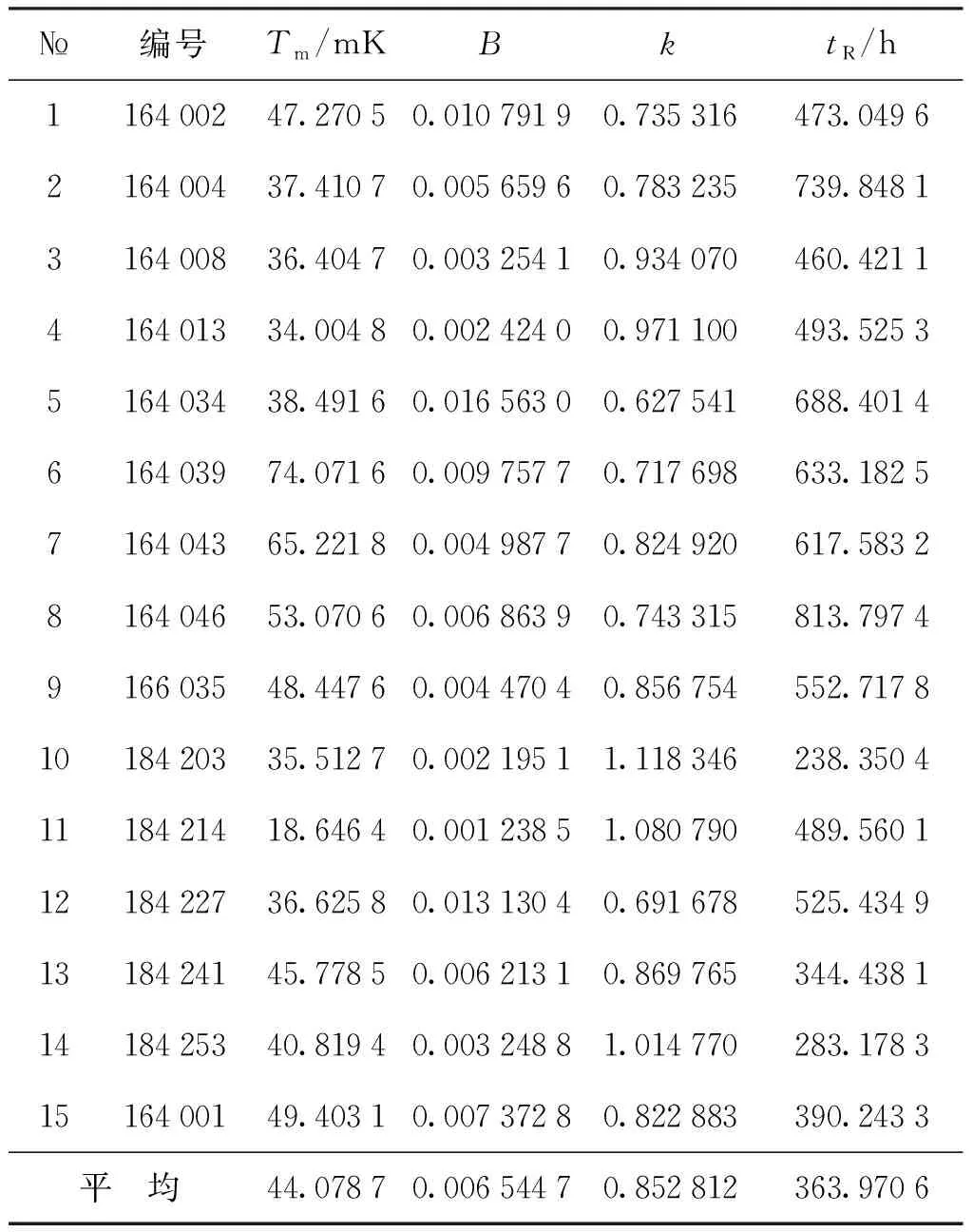
表1 15支SPRT退火后水三相点下各参数测量结果Tab.1 The results of each parameter of 15 SPRTsafter annealing at the triple point

由表1可知,15支标准铂电阻温度计退火在在水三相点电阻值对应的温度幅值变化范围为18～75 mK,退火特征时间为238～814 h,平均值分别为Tm=44.078 7 mK,tR=363.970 6 h。

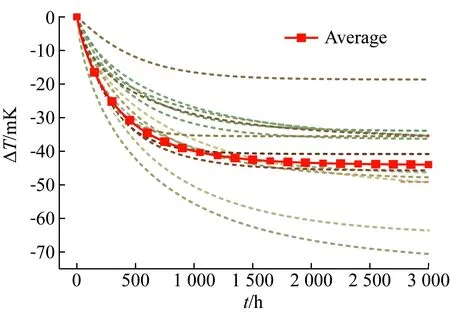
图4 15支温度计退火后水三相点温度变化理论曲线Fig.4 Theoretical curve of the temperature change at water triple point for 15 SPRTs after annealing

图5 15支温度计退火后水三相点无量纲温度变化理论曲线Fig.5 Theoretical curve of dimensionless temperature change at water triple point for 15 SPRTs after annealing

按照表1中参数,画出15支温度计的退火水三相点值、无量纲电阻值及双对数无量纲电阻值变化以及平均值理论曲线,并将退火时间推算至3 000 h,见图4～图6。

图6 15支温度计退火后水三相点双对数无量纲温度值变化理论曲线Fig.6 Theoretical curves of the double logarithmic dimensionless temperature change at water triple point for 15 SPRTs after annealing

由于每支铂电阻温度计在铂丝缠绕冷加工制作过程中经历的具体细节过程不完全相同,因此在后面进行的退火过程中水三相点值变化曲线也不尽相同,但是无量纲电阻值变化曲线相似,双对数无量纲电阻值变化也相似,无量纲电阻值曲线主要与退火参数B和退火指数k有关。

由水三相点值变化式(4)可得出退火过程中经过任意时间间隔Δt后的水三相点值变化的差值或稳定性,δ(ΔT)=ΔT(t+Δt)-ΔT(t),即：

δ(ΔT)=Tm{exp[-B(t+Δt)k]-exp[(-Btk)]}

(10)

取Δt=50 h,则间隔50 h的水三相点值稳定性随时间变化理论曲线见图7及表2。由图和表可知,退火平均时间400 h后间隔50 h的水三相点值平均稳定性在2 mK以内,650 h后的平均稳定性可以达到1 mK左右。

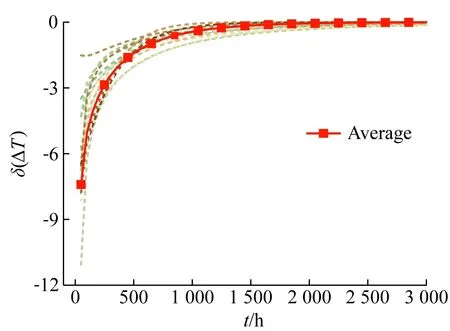
图7 15支温度计退火间隔50 h水三相点值的稳定性变化理论曲线Fig.7 Theoretical curve of the temperature stability change at water triple point for 15 SPRTs at the 50-hour annealing interval

若取Δt=100 h,则间隔100 h的水三相点值稳定性随时间变化理论曲线见图8及表2。由图和表可知,退火平均时间700 h后间隔100 h的水三相点值平均稳定性在2 mK以内,1 000 h后的平均稳定性可以达到1 mK左右。

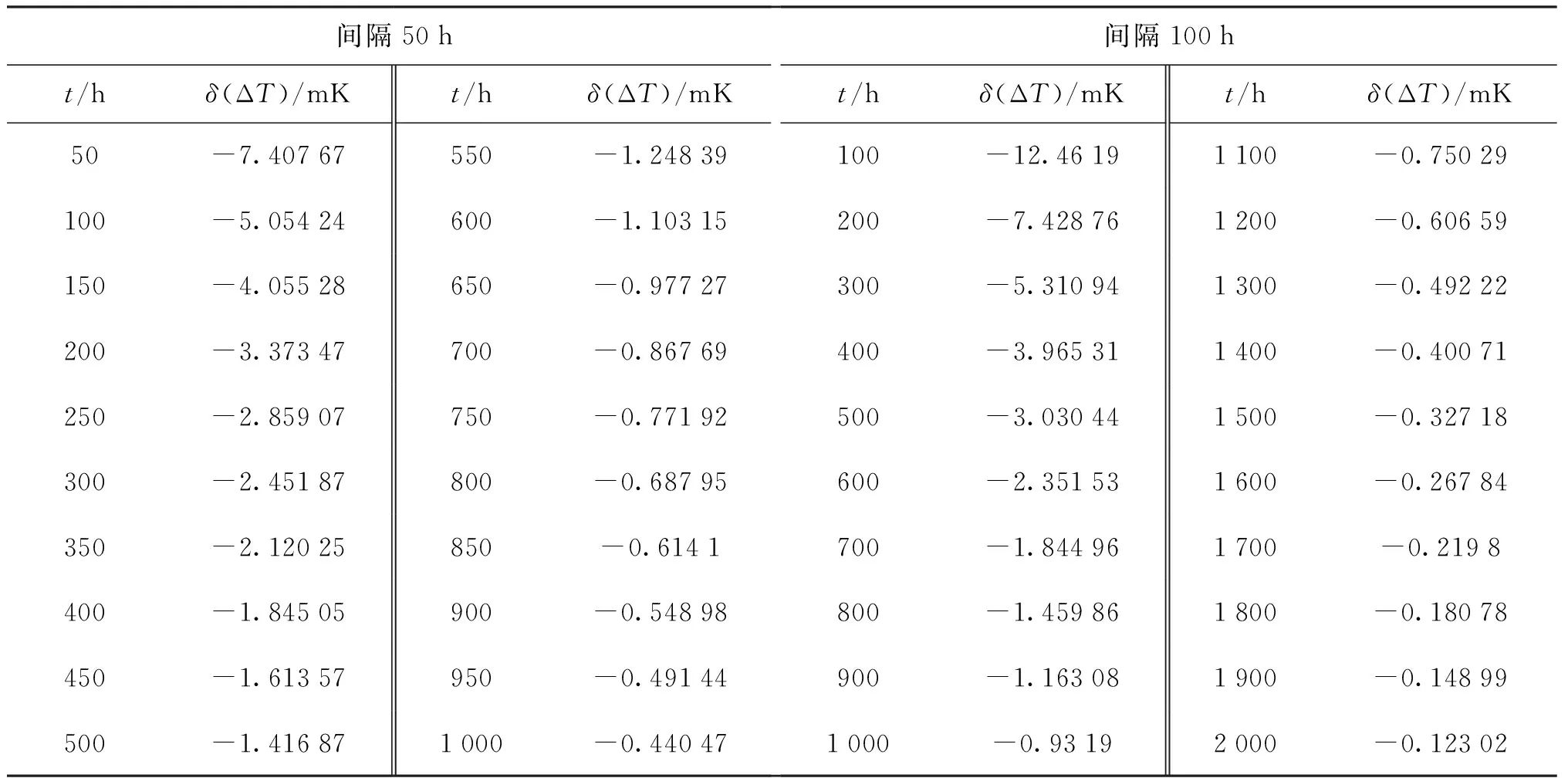
表2 间隔50 h和100 h的水三相点值平均稳定性变化理论结果Tab.2 Theoretical results of the average stability of the triple point of water at the 50 h or 100 h annealing intervals

图8 15支温度计退火间隔100 h水三相点值的稳定性变化理论曲线Fig.8 Theoretical curve of the temperature stability change at water triple point for 15 SPRTs at the 100-hour annealing interval

由图7和图8还可以发现,15支温度计退火水三相点值间隔一定时段的稳定性变化曲线与平均值曲线之间的偏差在逐渐减小,与平均值越来越靠近。因此平均值曲线在一定程度上可以反映出温度计稳定性的主要变化规律。

对于标准铂电阻温度计而言,退火后的水三相点值稳定性非常重要,可以通过稳定性计算公式(10)来研究和预测温度计的退火稳定性特性,退火平均值理论曲线可以为合理制定退火工艺时间提供理论预测和指导。

4 结 论

热处理工艺是新制SPRT获得高稳定性的关键[11]。退火过程中温度计电阻值随退火时间的变化规律主要依靠实验测量,缺乏理论指导。本文根据再结晶动力学中的相关理论,对水三相点电阻值或对应温度变化值随时间的变化趋势建立了理论模型计算公式。尽管每支铂电阻温度计退火过程中水三相点电阻值变化曲线不尽相同,但无量纲电阻值变化曲线相似,双对数无量纲电阻值变化也相似,主要与退火参数B和退火指数k有关。

理论计算结果表明,退火平均时间700 h后间隔100 h的水三相点值平均稳定性约为2 mK,1 000 h 后的平均稳定性可以达到1 mK左右。稳定性计算公式可以用来研究和预测温度计的退火稳定性特性,退火平均稳定性曲线在一定程度上可以反映出温度计退火稳定性的主要变化规律,可为合理安排制定退火工艺时间提供理论预测和参考。