基于高阶交错网格有限差分的隧道超前探测地震波场模拟

张焕钧，陈祖斌，李 昊，杨兴林

(吉林大学仪器科学与电气工程学院, 吉林 长春 130026)

0 引言

隧道施工时常发生塌方、突水等地质灾害事故，需要有效的隧道超前探测手段来对未开采区域进行预报，以减少生命和财产的损失。TSP(tunnel seismic prediction)法是一种常用的利用地震波进行隧道探测的有效手段[1]，为了给其提供良好的模拟数据，并检验相应TSP法反演的准确性和稳定性，需要准确、高精度的地震数值正演模拟提供数据支撑。

目前，地球物理领域常用的正演方法有射线追踪法[2]、积分方程法、有限元微分方程法[3]和有限差分微分方程法。其中，射线追踪法较为直观，但要求速度模型变化要平缓；积分方程法精度高，但数值求解困难；有限元微分方程法网格划分灵活，但运行效率低下；而使用有限差分法求解波动方程模拟波场是计算效率和精度较高的正演模拟手段，非常适合实际工程应用。20世纪80年代，Dablain[4]先提出了高阶有限差分求解波场的方法；Jastram等[5]又提出了变步长有限差分法，提高了运算效率；之后，国内学者[6-7]提出了交错网格有限差分法，进一步提高了波场模拟的精度。随着计算机效率的提高，近几年学者们开始对复杂地质结构进行模拟，包括孔隙介质[8]、黏弹性介质[9]、各向异性介质[10]等，还有一些学者专注于使用GPU加速正演算法的运行[11]，但与实际应用场景(如隧道探测、矿井探测等)结合较少。

本文提出的隧道探测正演模拟服务于GEI-TSP隧道超前预报系统，该系统采用少炮多道的采集系统，具有成本低、安全性好的优点。本文在该系统的基础上进行数值模拟计算，并结合隧道模型给出相应的模拟结果。

1 数值模拟

1.1 弹性波方程与交错网格有限差分

地震波数值模拟可以采用声波方程，如一阶速度-应力弹性波方程、二阶位移弹性波方程等。由于隧道探测多为多波多分量地震信号的采集，对介质的密度和速度较为敏感，且只需要探测掌子面后方平行或倾斜于掌子面的断层、裂隙，故本文选择二维一阶速度-应力弹性波方程进行模拟。假设介质各向同性，密度不均匀，则其表达式为[12]：

(1)

式中：x为平行掌子面方向；z为垂直掌子面方向；ρ为介质密度；vx、vz分别为速度在x、z方向上的分量；τxx、τzz分别为x、z方向的正应力；τxz为切应力；μ、Λ为拉梅系数，与传播介质的速度、密度相关，其表达式见式(2)—(3)。

Λ=ρ(vp2-2vs2)；

(2)

μ=ρvs2。

(3)

式(2)—(3)中：vp为介质的纵波速度；vs为介质的横波速度。

对于式(1)，本文使用二维交错网格有限差分法进行求解。有限差分的原理是用网格剖分的办法将方程离散，用差分项代替微分项后再代入边界条件进行求解，得到一个基于网格精度的数值解。而交错网格的原理就是将速度、应力定义在一个交错了半个空间步长的网格上，这么做可以在保证精度的同时大大提高计算的效率，减少频散的产生。交错网格有限差分示意如图1所示。

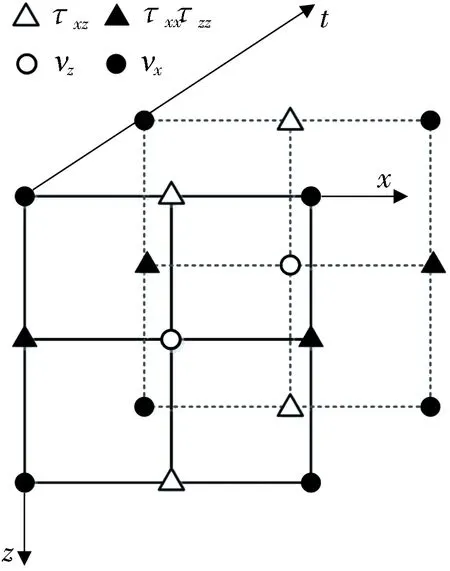
图1 交错网格有限差分示意图

对于时间2阶、空间2N阶精度的有限差分法，式(1)中的空间微分项应该用差分格式(4)来替代，时间微分项用差分格式(5)来替代。

(4)

(5)

式(4)—(5)中：f为需要进行微分的速度和应力分量； Δx、Δz分别为x、z方向的空间步长；t为模拟时间； Δt为时间步长；an为差分系数，由式(6)确定。

(6)

式(4)的截断误差

Δf=C2Nf2N+1xΔx2N+1+O(Δx2N+2)。

(7)

1.2 有限差分数值模拟中的一些问题

1.2.1 稳定性

差分方程的稳定性是差分方程求解波动方程数值解的基本问题。交错网格差分精度应该满足式(8)，才能使得数值计算过程稳定。

(8)

式中γ为稳定性阈值，其值见表1。

表1 γ与空间差分阶数的关系[13]

1.2.2 频散

频散是差分方程近似微分方程过程中出现的不同波数的分量以不同速度传播的现象，包括空间频散和时间频散。由于稳定性(式(8))的要求，Δt与子波周期的比值很小，所以频散主要由空间频散造成[14]。交错网格差分方程求解一阶弹性波方程的空间频散曲线公式如下：

(9)

式中p、q应满足条件见式(10)。

(10)

式中：v0为未发生频散情况下的纵波速度；υ为泊松比；λ为波长；θ为传播方向。

υ取0.25、θ取45°时，不同阶数交错网格差分方程的空间频散曲线如图2所示。可以看出，在频散问题上，交错网格法相比于常规网格有大幅度的改进，并且差分精度的提升也能明显改善有限差分法的频散问题。本文选择100 Hz雷克子波作为震源，在最大纵波速度vp=4 000 m/s的情况下，波长λ为40 m，则Δx/λ=0.025，在这个步长波长条件下，频散是十分微弱的。高阶差分和交错网格对于频散问题改进的波场快照示意如图3所示，可以看出提高阶数和使用交错网格法可以有效地改善频散问题。

此外，本文还使用通量传输校正法[15]对频散进行进一步的压制。该方法假设波形中所有的极值点均是由数值频散所引起的，在迭代求解波长过程中通过计算漫射通量对波形进行平滑处理并压制频散；之后，再计算反漫射通量补偿平滑处理时的振幅损失。针对一阶速度-应力弹性波方程的通量传输矫正方法，只需要在速度项上进行校正，应力项通过速度-应力的关系自然会被矫正，这样就提高了计算效率。

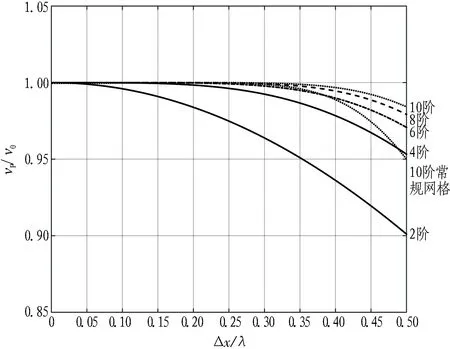
图2 不同阶数交错网格差分方程的空间频散曲线

1.2.3 边界条件

由于计算机计算能力有限，只会在掌子面前方一定长度的区域进行数值模拟，此时人为划分的边界会产生本不存在的虚假反射，所以需要一定手段消除这一反射。Collino等[16]将Berenger提出的PML吸收边界应用在地震波领域，其原理是在波动方程中引入一个变化的衰减函数d(s)，在有限的吸收区域将虚假的反射衰减到不会影响到正演区域的数值大小。该函数的系数部分应与介质速度成正比，与吸收厚度成反比。整个函数应是一个与正演区域边界距离s有关的凹函数，因为凹函数前期增长慢，与正演区域完美匹配，几乎不产生反射，后期增长快，衰减效率高。此前学者[17-18]提出的衰减函数都依赖于经验，且衰减过程不平稳，故本文提出一种新的衰减函数如下：

(11)

式中：L为吸收区域总层数；s为距正演区域的层数；R=0.000 1。

为了体现上述衰减函数的吸收效果，本文将其与目前广泛使用的余弦衰减函数、指数衰减函数和二次幂衰减函数做对比测试。测试的区域是边长为150 m的正方形，震源位置在区域的中心。4种衰减函数的波场快照如图4所示，其中对振幅求取了绝对值，便于比较吸收效果。t=80 ms时4种衰减函数的波场快照中经过吸收后剩余峰值的最大值和计算后的反射率见表2。

(a) 4阶普通网格 (b) 10阶普通网格

表2 4种衰减函数吸收效果对比

图4所示的是中心震源激发后经过4个边和4个角吸收后反射回来的波。结合表2数据可以看出，几种衰减函数都有效压制了人为边界造成的反射，但余弦函数和幂函数在衰减前中部反射过大，指数函数在衰减末端反射过大。而本文提出的衰减函数，衰减更为平缓，将进入吸收边界的波的能量均匀吸收和反射，衰减后峰值最小，衰减效果最好。

1.2.4 计算效率

计算效率是在实际数值计算中不得不考虑的问题，尤其是在需要实时数据处理或者程序运行环境不佳的情况下。在正演模拟中，模拟区域的范围(包括吸收边界)与模拟的时长往往是固定的，此时数值计算效率就只与网格剖分精度Δx、Δz、Δt和差分阶数2N(空间)、2M(时间)有关。

假设模拟区域宽为X、长为Z，模拟总时长为T，则数值计算的空间复杂度为O(n)，时间复杂度为O(m)，其中n满足式(12)，m满足式(13)，式中常数10代表了速度和应力5个变量，而每个变量都在x和z方向上有分量。

(12)

(13)

虽然式(13)中数值计算的时间复杂度与差分阶数和网格精度呈比例关系，但实际上由于稳定性的要求，提高空间差分阶数N或者缩小网格Δx、Δz都会进一步降低Δt，因此时间复杂度会进一步提高。这意味着过于追求计算精度可能会损失更多的计算效率。

根据以上4点问题的论述，本文算例采用时间2阶空间10阶交错网格差分法。根据式(6)得到的空间10阶精度下差分系数an见表3；根据稳定性条件(式(8))，本文算例选择空间网格剖分精度Δx=Δz=1 m，时间网格精度Δt=0.1 ms，模型最大纵波速度vp=4 000 m/s。

表3 10阶精度差分系数

2 隧道超前探测正演算例

本文按照GEI-TSP隧道超前预报系统的要求，在掌子面附近安放炸药震源，在隧道震源一侧安放16道检波器，最小炮检距为15 m，道间距为2 m。单炮多道采集示意如图5所示。本文以此为基准，分别建立层状模型和空洞模型来验证正演数值模拟的有效性。

图5 单炮多道采集示意图

2.1 层状模型

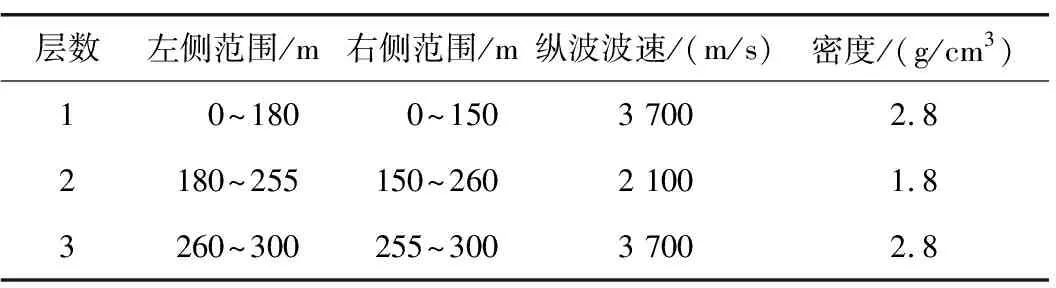
表4 层状模型参数

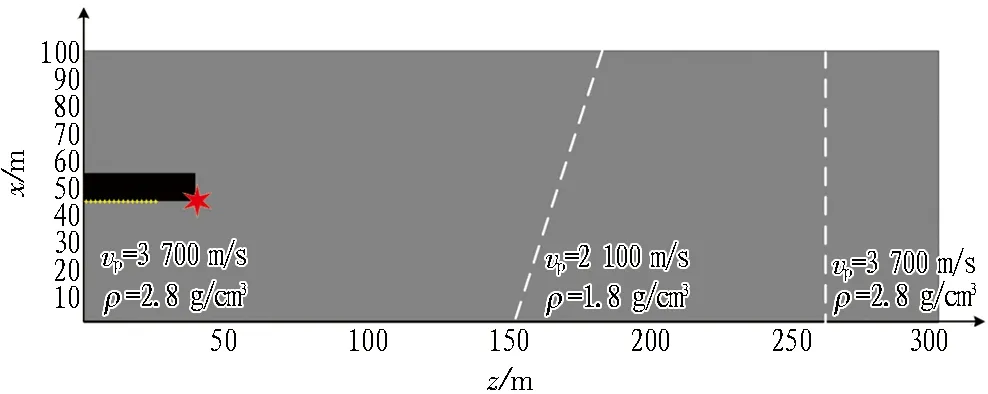
图6 层状隧道模型示意图

图6中正演区域长(z方向)300 m、宽(x方向)100 m；黑色部分为隧道，长45 m、宽10 m；红色点为震源点，震源使用100 Hz雷克子波，震源有2 m的埋深；黄色区域安放检波器共16个，最小炮检距为15 m，检波器与检波器之间的距离为2 m。数值计算时，隧道的边界设置为一个刚性反射界面，震源加载在弹性波方程的速度项上。层状模型波场快照如图7所示。

由图7可知：t=30 ms时，地震波沿均匀介质球面扩散，由于炸药有2 m的埋深，会与隧道界面产生1次反射；t=80 ms时，地震波波前已经过第1个倾斜反射界面，产生了反射波和透射波；t=120 ms时，可以清楚地看到第1个界面反射波和透射波均有P波和S波；t=170 ms时，地震波经过第2个反射界面。

层状模型共炮点道集如图8所示，可以明显地看到能量较强的直达波。将反射波波分放大后，也可以清楚地观察到2个界面的反射P波和S波以及最初隧道界面反射在反射界面产生的反射波，尤其是在x分量上，反射S波更加明显。

2.2 空洞模型

建立空洞隧道模型如图9所示。这种模型可以代表隧道前方有一区域内介质的密度和地震波传播速度极低，如溶洞、水体等。

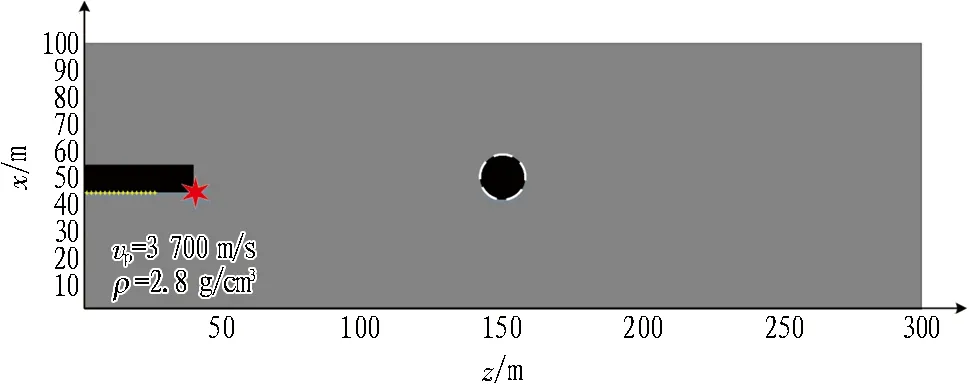
图9 空洞隧道模型示意图

空洞位于掌子面正前方105 m的位置，形状是一个直径为15 m的圆，其内部介质密度和速度均为0。空洞外部为均匀介质，密度ρ=2.8 g/cm3，纵波速度vp=3 700 m/s，其余参数与层状模型一致。空洞模型波场快照如图10所示。

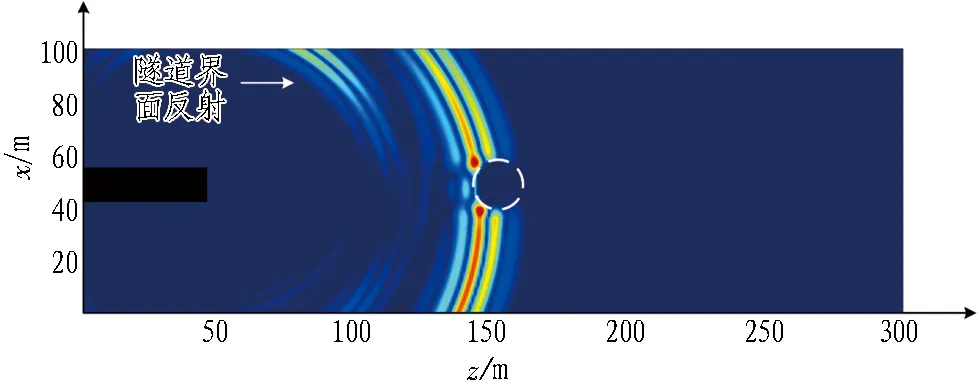
(a) z分量(t=65 ms)

(b) z分量(t=120 ms)

(c) x分量(t=65 ms)

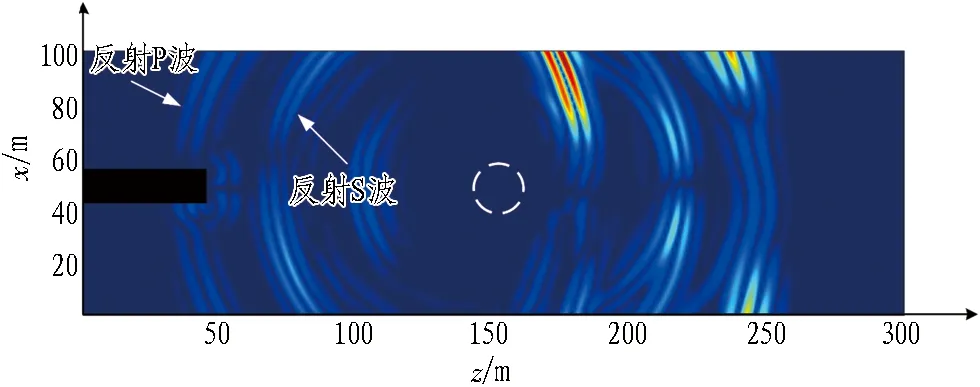
(d) x分量(t=120 ms)

由图10可知，t=65 ms时，地震波沿均匀介质球面扩散后，地震波波前与圆形空洞相接触。在t=120 ms的波场中可以清晰地看到反射的P波和S波以及绕过空洞继续向后传播的弹性波。

空洞模型共炮点道集如图11所示。图中可以明显地看到反射P波与反射S波，证明本文所建立的正演模型适用于介质中含有空洞的情形。

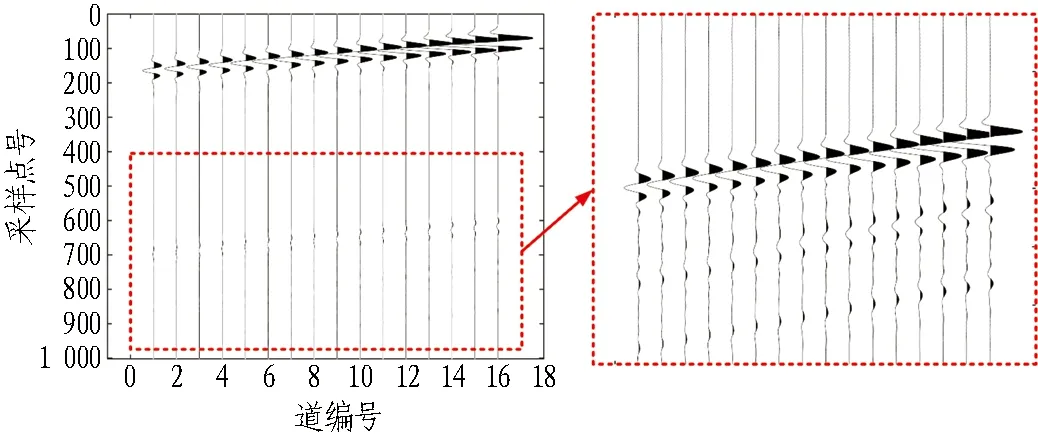
(a) z方向分量

(b) x方向分量

3 结论与讨论

波动方程正演是在多种因素制约下进行的波场模拟，其需要在兼顾稳定性、频散和精度的同时，尽可能地保证计算效率。本文提出的高阶有限差分隧道超前探测正演模拟得到了符合预期的结果，并得出以下结论：

1)使用高阶交错网格有限差分求解一阶速度-应力弹性波方程，对隧道模型进行的模拟效果良好，所获得的模拟数据可以为隧道超前探测的反演提供数据和模型支撑。

2)PML吸收边界的衰减函数可以借鉴已有函数，但需要结合实际参数来修改衰减函数，这样才能有好的吸收效果，从而减小吸收边界宽度，提高计算效率。

使用有限差分求解波动方程的网格精度和差分阶数应该在满足稳定性要求的情况下尽可能地压制频散，但又不能过于牺牲计算效率。所以，如何在保证数值计算结果真实的情况下尽可能降低计算成本，是进一步研究所应该探讨的问题。