藏东南波堆藏布江流域古乡冰期冰川重建

覃长雄，许刘兵，谢金明，周尚哲

（1.华南师范大学 地理科学学院，广东广州 510631；2.兰州大学 资源环境学院，甘肃兰州 730000）

0 引言

冰川是寒冷气候的产物，对气温和/或降水变化十分敏感［1］，古冰川相对现代冰川的物质平衡线高度（equilibrium-line altitude，ELA）、面积、长度、以及体积等特征参数的变化，对了解古气候和预测未来气候变化至关重要。其中，现代冰川的各项特征参数可根据实地观测、测量、遥感影像解译等方法直接估算得到，对古冰川而言，通常是根据现代冰川与当前气候环境要素（如气温、降水、地形等）的统计关系，再结合冰川地貌和年代学去反演过去不同时期冰川的各项关键参数。从目前的研究现状来看，对古冰川发育环境及特征参数的重建研究主要集中在末次冰期最盛期（Last Glacial Maximum，LGM）以来，主要原因是LGM以来的冰川地貌保存相对完好，地质年代也能准确的测定。

“古乡冰期”是20世纪80年代由李吉均等［2］提出来的冰期概念，同时提出的还有“白玉冰期”，这两个冰期名称在青藏高原第四纪冰川作用众多地方性冰期名称中非常具有代表性，数十年来一直被广泛沿用。其中，古乡冰期指代的是传统意义上的“倒数第二次冰期”，已有的宇宙成因核素10Be地表暴露测年结果［3］显示其发生于海洋氧同位素阶段（marine oxygen isotope stage，MIS）6。虽然古乡冰期概念已被众人接受，且发生年代也已界定，但古乡冰期命名地即藏东南波堆藏布江流域的冰川作用规模（如范围、冰厚及冰量等）和ELA等关键参数仍有待进一步考证。本文在多次详尽野外调查的基础上，结合高清遥感影像/卫星照片及定量测年结果，对波堆藏布江流域古乡冰期的冰川作用范围进行了重建，并进一步尝试运用冰面纵剖面（glacier surface profile，GSP）模型、积累区面积比率（accumulation area ratio，AAR）法和末端-源头高度比率（toe-toheadwall altitude ratio，THAR）法等方法对波堆藏布江流域“古乡冰期”的古冰川特征参数进行重建。

1 古乡冰期冰川遗迹及其年代

波堆藏布江发源于念青唐古拉山东段南坡（29°89′～30°67′N、95°08′～95°96′E，图1），流域面积约1.46×104km²，邻近雅鲁藏布江大拐弯，处于南亚夏季风进入高原的水汽通道上。流域内的高山（最高峰则普海拔6 364 m）迎风面降水丰富，使得该区域发育了规模庞大的第四纪和现代冰川，冰川ELA和冰川末端高度基本处于同纬度的最低值［2］。

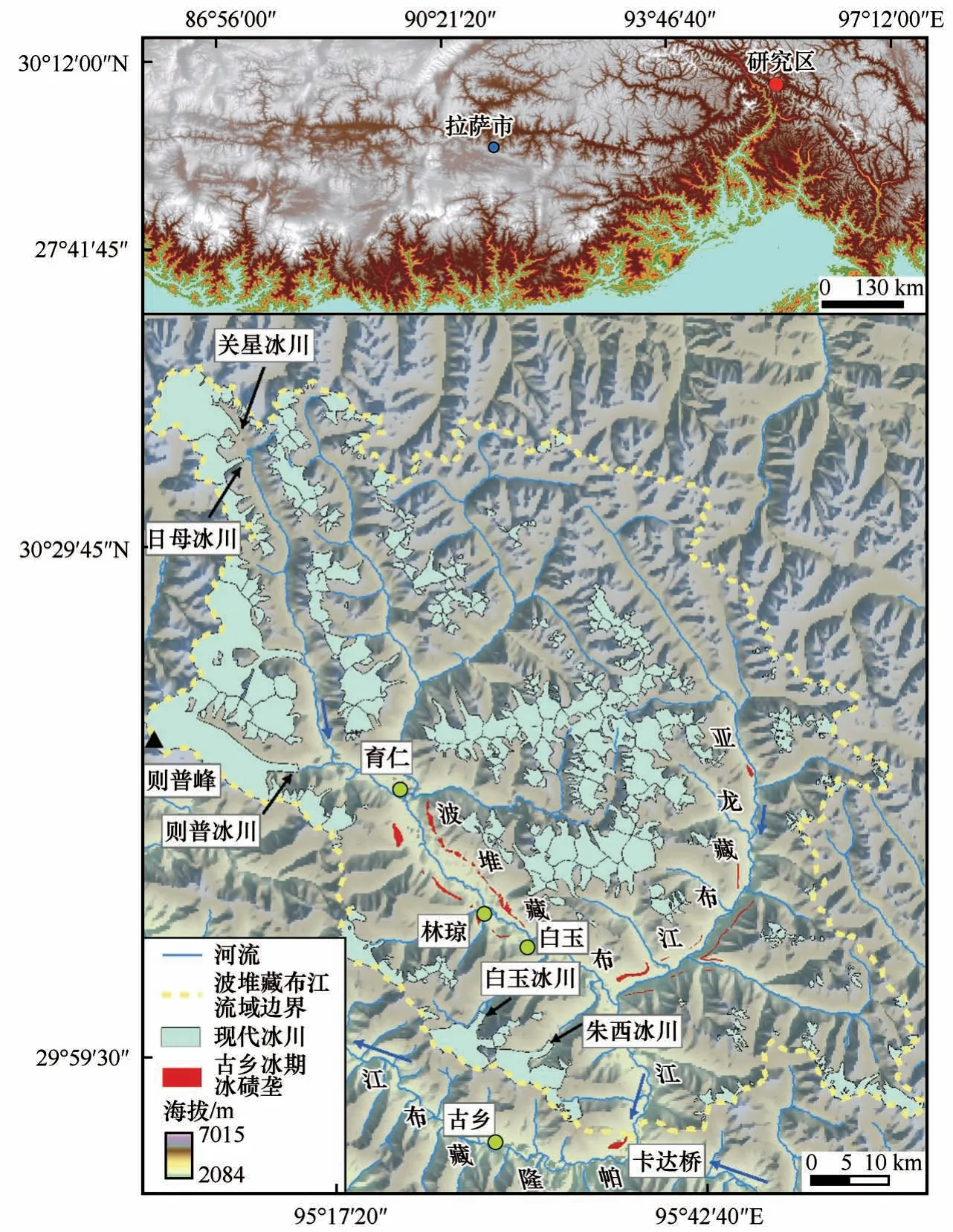
图1 波堆藏布江流域位置及流域内现代冰川［4］和古乡冰期冰碛垄分布图Fig.1 Map showing location of the Bodui Zangbo River catchment，modern glaciers［4］，and moraines of the Guxiang Glaciation within the catchment

古乡冰期指的是传统意义上的“倒数第二次冰期”，由李吉均等［2］于20世纪80年代提出，其命名地位于藏东南波堆藏布江与帕隆藏布江交汇处下游约17 km的古乡镇，即古乡冰期时，流域内支谷冰川汇入主谷（即波堆藏布江谷地），形成复合型山谷冰川，冰舌到达了古乡镇附近，遗存有较大规模的终碛-侧碛垄。

除古乡镇一带的冰碛垄外，波堆藏布江主谷两侧亦保存有古乡冰期的沉积物（图1）。保存在两侧谷坡、形态完好且规模宏大的侧碛垄从上游育仁一直延伸至白玉村附近，拔河高度从550 m降至260 m左右［图2（a）和（b）］；自白玉向下游保存不甚理想，只见部分谷肩上残存有零星的冰碛物；但在波堆藏布江汇入帕隆藏布江处的卡达桥附近，尚完好地保留着拔河约200 m、长约3.2 km的高大侧碛垄，其上分布着大量的花岗岩漂砾［图2（c）］。周尚哲等［3］对卡达桥附近古乡冰期冰碛垄进行了10Be暴露测年，测年结果（约130 ka）显示古乡冰期发生于MIS 6。除波堆藏布江主谷外，古乡冰期冰碛垄在支谷亚龙藏布江两侧谷坡上也有保存，其中，亚龙藏布汇入波堆藏布处的侧碛垄保存得最为完整［图2（d）］。亚龙藏布江北岸的侧碛垄垄脊非常典型，从谷口往上游延伸约4.5 km，拔河高度由200 m升至320 m，而谷口南岸的侧碛垄因受到支沟的侵蚀，垄脊较为平坦。冰碛垄在上游也有断续保存，直到海拔3 700 m处，此处拔河约500 m。可见，古乡冰期时，波堆藏布江流域内支谷冰川都汇入了主谷，形成了主干长达100 km左右的复合型山谷冰川，冰川规模可能为现代的数倍［2］。

图2 育仁（a）、林琼（b）、卡达桥（c）和亚龙藏布谷地（d）的古乡冰期冰碛垄照片Fig.2 Photos of moraines deposited in the Guxiang Glaciation（Moraines in a，b，c，and d are located near Yuren，Linqiong，Kada Bridge，and Yalong Zangbo Valley，respectively）

2 研究方法

2.1 古乡冰期时冰川范围的划定

在多次详尽野外调查的基础上，结合已有冰川地貌年代学、高清遥感/卫星影像以及数字高程模型（digital elevation model，DEM），对古乡冰期冰川作用范围进行了重建（图3）。在划定古乡冰期冰川范围时，存在冰碛地貌的地方比较容易确定冰川作用范围，例如沿着波堆藏布江主谷从则普冰川至古乡镇这一段，以及亚龙藏布江与波堆藏布江交汇口附近，可以按照谷地两侧古乡冰期侧碛垄确定古冰川的作用范围（图1）。在古乡冰期冰碛地貌保留不理想甚至完全被侵蚀破坏的地方，如流域内的西南部、西北部以及中部，结合现代冰川的分布范围来大致划定古乡冰期冰川作用范围。而在流域内的东北部，既无明确的古乡冰期冰碛地貌，也没有现代冰川分布，主要依据形态清晰的冰斗和槽谷来划定古冰川作用范围。波堆藏布江流域内仍然存在还未定年或无法定年的冰碛垄，要准确地确定古乡冰期时的冰川作用范围，仍需进一步实地考察冰川沉积地貌以及进行相关的定年研究。因此，本文采取上述策略来界定古乡冰期冰川作用范围，可能与实际情况存在出入，但依据划定的古冰川范围估算出的古乡冰期ELA结果来看，与Zhou等［5］的研究结果基本一致（见3.2节）。

图3 古乡冰期时波堆藏布江流域古冰川范围重建（彩色实线代表35条中流线分布，红色虚线代表流域边界）Fig.3 Reconstruction of glacier outline in Guxiang Glaciation in the Bodui Zangbo River catchment（The solid colored lines represent glacier centerlines，and the dotted red line represents the boundary of the Bodui Zangbo River catchment）

2.2 古冰川模拟原理

将根据上文方法得到的古乡冰期冰川作用范围导入ArcGIS中，与分辨率为30 m的DEM数据（ALOS World 3D-30 m，https：//www.eorc.jaxa.jp/ALOS/en/aw3d30/index.htm）叠加，可得到古冰川的面积。

后运用冰面纵剖面模型模拟古乡冰期冰川的冰面形态和冰厚等特征参数。冰面纵剖面模型由Schilling等［6］提出，后经Benn等［7］改进，现已被广泛运用于各地（含青藏高原及周边山地）古冰川形态的重建［8-12］。

此模型基于的假设为冰川是理想的塑体，其形变由冰的重量及冰表面梯度引起的驱动应力（driving stress，τd）和冰川底部的屈服应力（yield stress，τy）的变化引起。当驱动应力大于屈服应力时，冰川发生运动；当驱动应力小于屈服应力时，就不会发生冰川的运动，但冰川会变厚从而增加驱动应力。为了保持冰川的稳定状态，即τy=τd，冰川的厚度会不断进行调整，从而引起驱动应力的变化。基于此得到了下列表达式。

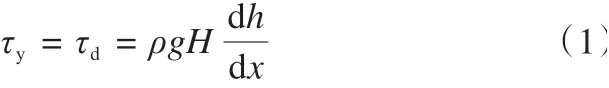
式中：ρ为冰川密度（900 kg·m-3）；g为重力加速度（9.81 m·s-2）；H为冰川厚度；h为冰表面高程；x为水平坐标（以冰川末端为原点，冰底和冰面高程为纵轴，距冰川末端的长度为横轴的坐标系）。有时用sinα代替，α为冰川表面坡度［13］。根据以上等式可求出沿着中流线的冰川厚度H，结果为抛物线。

但该式不适用于冰川坡度较大的地区。对于不规则的冰下地形，Benn等［7］指出必须沿着中流线按连续的点（编号1，2，…，i，i+1，i+2）计算，冰的表面坡度表示为

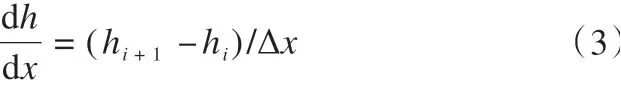
式中：Δx为每个点的间隔距离，本文取Δx=200 m。

因此，由式（1）和式（3）得

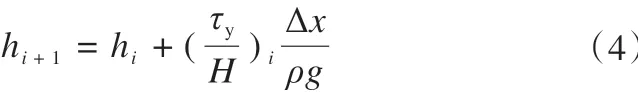
式中：H=h-B，B为冰川底部高程，此式可以解出冰面高程h。

为了解决冰舌处冰厚为0的问题，van der Veen［14］进一步推导得到

但该模型是以冰盖出发进行推导的，冰盖不受山谷两侧阻力的约束，其流动需要的驱动应力等于冰川底部剪切应力。而山谷冰川则需要考虑山谷两侧阻力的影响，因此引入形状因子f。

式中：τB为底部剪切应力。

在冰川中流线处，τB=τd，f为

式中：A为冰川横截面面积；H为冰厚度；p为横截面的“冰川周长”［15］；f的取值范围一般为0.4～1［8］。此时的驱动应力大于同等条件下冰盖流动所需要的驱动应力，在计算时，需要把式（4）中的τy用τy/f替换。

2.3 古冰川模拟过程

使用ArcGIS软件并结合DEM数据以及研究区的谷歌地球（Google Earth）影像图，在古冰川范围上提取出中流线，为了使中流线上插值点分布范围更全面，减小插值误差，人工选取了23条分布在面积较大的现代冰川上的中流线和12条分布在主谷位置的中流线（合计35条冰川中流线，图3）。在Arc-GIS中，按等距离（Δx=200 m）对中流线进行分割，把分割得到的线段转化为点，最后提取每个点的高程数据，古冰川模拟流程如图4。

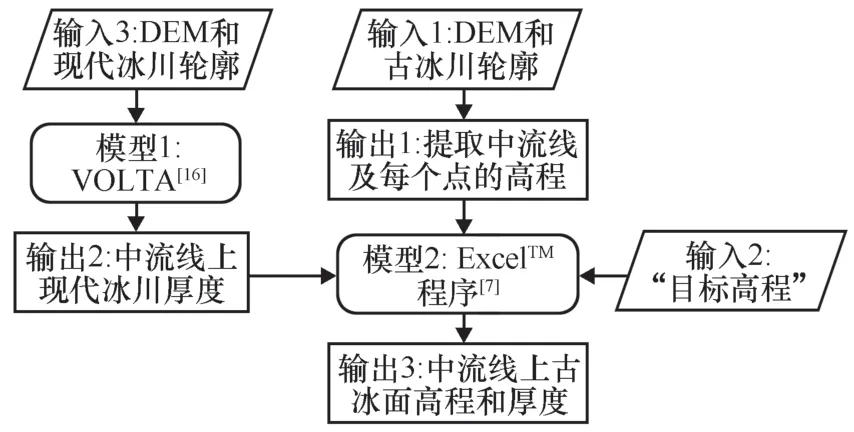
图4 古冰川模拟流程图Fig.4 Flow chart of paleo-glacier simulation

在此ExcelTM表格程序中进行古冰川表面高程模拟时，步长（Δx=200 m）、冰的密度（ρ=900 kg·m-3）、重力加速度（g=9.81 m·s-2）是已知的，而B为冰底地形高程，存在现代冰川的地方需要减掉其厚度。输入的剪切应力τy一般取值100 kPa，根据谷歌地球影像图，可求得终碛-侧碛垄的高程数据作为“目标高程”，将其与中流线上相应点的高程对应起来。下面将以中流线E4（图3，古乡至关星冰川北部顶端）为例子，模拟结果见图5。

模拟过程中，从下游（古乡）至上游（关星）沿着中流线作出几道横剖面，计算每一段的形状因子［图5（d）］并插值，之后通过不断调整中流线上各点的剪切力，使冰面高程与“目标高程”（终碛-侧碛垄高度）接近一致［图5（c）］。

图5 根据冰川中流线E4模拟的冰川表面高程和其他参数Fig.5 Characteristic parameters of the glacier reconstructed from the glacier centerline E4（Figure a，b，c，and d represents basal shear stress，ice thickness，surface elevation，and shape factor，respectively）

使用上述模拟过程，对其他34条中流线进行模拟，将模拟结果分别用反距离加权（inverse distance weight，IDW）、泛克里金（universal Kriging，UK）和普通克里金（ordinary Kriging，OK）插值法进行插值，最终得到古冰面高程，而古冰川厚度可由模拟古冰面高程减去古冰川冰底高程，结果见图6。

2.4 冰川ELA估算方法

由Meier［17］提出的AAR法被广泛用于计算古冰川和现代冰川的ELA，这一方法的关键是选择合适的AAR值。研究表明，分布于不同纬度的冰川，有不同的AAR值。中高纬度冰川的AAR值介于0.5～0.8［18］或0.55～0.65之间［19］，而低纬地区则可能高达0.8［20］。AAR法假定冰川物质平衡随高度的变化趋近于一条直线，并且考虑了冰川的面积-高程信息。Kern等［21］认为冰川面积S与AAR值之间正相关，且呈对数变化关系：AAR=0.0648×lnS+0.483。对于一些数据缺乏的地区，当S为0.1～1 km²时，AAR=0.44±0.07；当S为1～4 km²时，AAR=0.54±0.07；当S大于4 km²时，AAR=0.64±0.04。Kaser等［22］认为热带地区无积雪覆盖的冰川最佳AAR范围在0.65～0.70之间，且这个范围对于热带有积雪覆盖的冰川同样适用，地貌证据也表明了这个取值范围同样适用于古冰川。

本文以朱西冰川、白玉冰川、则普冰川、日母冰川和关星冰川为例，在已有冰川编目数据的基础上，计算这5条冰川AAR的平均值，并将得到的AAR平均值用来估算古乡冰期时冰川的ELA。具体操作如下：①根据第一次冰川编目［23］这5条冰川的积累区面积和总面积计算AAR值，取此AAR的平均值来估算古乡冰期时的冰川ELA；②根据得到的AAR值和第二次编目的冰川范围来计算各冰川的ELA（表1），其平均值用于下文中选取THAR值。考虑到这些冰川上部宽、下部窄，粒雪盆（积累区）与冰舌（消融区）都发育正常［24-25］，因此用这5条冰川AAR的平均值（0.73）来恢复古乡冰期时的冰川ELA。

THAR法也常用于估算古冰川和现代冰川的ELA，THAR值为ELA与冰川最低点高程之差和冰川最高点与最低点高程之差的比值。但该方法并未涉及到冰川的物质平衡或者冰川的面积-高程信息，THAR值的选取有一定的主观性［26-27］。Charlesworth［28］、Manley［29］曾使用冰川的中值高度来代替ELA。THAR值小于0.5时的ELA小于中值高度［30-33］。Meierding［32］在研究科罗拉多冰川时，认为在0.35～0.40之间的THAR值比较合适。使用该方法估算古冰川ELA时，古冰川的末端高程主要根据冰川终碛的高度计算，即采用沿终碛顶端的最低高度作为冰舌的最低高度［24］；但最高高程不容易确定。为了选取合适的THAR值估算现代冰川和古冰川ELA，本文以第二次冰川编目［4］时观测的5条现代冰川（分别为朱西冰川、白玉冰川、则普冰川、日母冰川和关星冰川）为例（图1），将每条冰川上缘处的最高点作为最大高程，使用不同THAR值估算其ELA，估算结果见表2。结果显示，相同的THAR值下这5条冰川的ELA有着类似的变化趋势，即随着冰川海拔的增高其ELA增大，本文取这5条冰川ELA的平均值来代表整个流域的ELA。继而与第二次冰川编目下这5条冰川ELA（表1）的平均值4 451 m比较，发现THAR=0.35时二者比较接近（表2），因此，在重建古乡冰期ELA时，THAR值取0.35。

表1 第一次冰川编目［23］下波堆藏布江流域内5条现代冰川的AAR值及估算的第二次冰川编目［4］下各ELA值Table 1 The five modern glaciers AARvalues in the Bodui Zangbo River catchment in glacier inventory of China［23］and their estimated ELA values in second glacier inventory of China［4］

表2 波堆藏布江流域不同THAR值下的5条现代冰川ELA估算结果Table 2 ELA estimates of five modern glaciers under different THAR values in the Bodui Zangbo River catchment

3 结果与讨论

3.1 冰川规模变化

从中流线E4上的剪切力分布［图5（a）］发现，下游（距冰川末端的长度为0～45 km）剪切力变化较小，中游（距离冰川末端的长度为45～75 km）剪切力变化较大，上游（距离冰川末端的长度为75～120 km）剪切力较小，总体分布在7～120 kPa之间。经过计算，剪切力τy平均值为61.3 kPa，平均形状因子为0.75，等效平均剪切力τy/f为81.7 kPa，在剪切力合理取值范围内（50～150 kPa）［13］。图5（b）是冰面高程与“目标高程”相吻合时的冰川厚度分布，由图5（c）中冰面高程与冰底地形高程相减所得。可以从图5（b）和5（c）看出，从下游到上游，冰川厚度总体上呈增大的趋势，其最大值分布在上游，但临近冰川陡峭的后壁时厚度迅速减小。另外，下游地形较为平缓而中上游地形起伏较大。一般来说，地形平缓的下游更容易积累冰川，但在下游主谷内冰川厚度较小，从白玉村往上游［图5（c），距离末端50 km以上］冰川厚度逐渐增大，则普村之后冰川厚度基本维持着很大的值，这种趋势在图6（d）中也很好地体现了出来。从图6（a）～（c）中可以得知当时的ELA大致分布在则普村（图1则普冰川末端）附近，因此冰厚的这种分布是合理的。

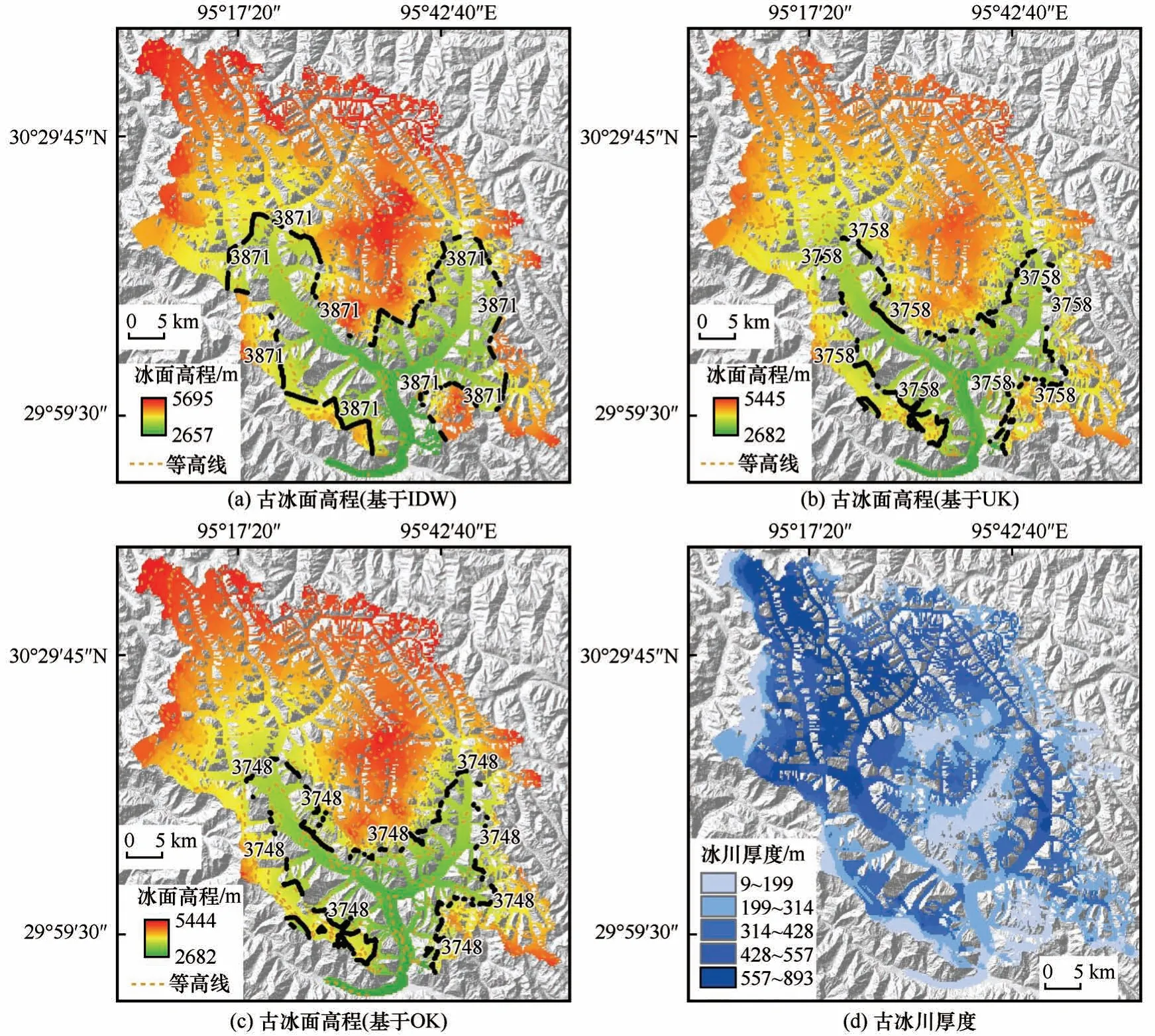
图6 古冰面高程（a，b，c）和古冰川厚度（d）模拟结果以及不同古冰面高程下的ELA重建结果（a，b，c中的黑线）（a，b，c分别为根据IDW、UK和OK插值法得到的古冰面高程）Fig.6 The modeled glacier surfaceelevation（a，b，c）and glacier thickness（d）and reconstructed ELAs（black linesin a，b，c）based on different glacier surface elevation（Figures a，b，c show the glacier surface elevation using IDW，UK，and OK interpolation methods，respectively）

通过对其余34条中流线的模拟，可以重建古乡冰期时古冰川的表面高程和冰川厚度（图6），大致估算出古乡冰期时波堆藏布江谷流域内冰川的形态参数，即流域内平均冰川厚度约360 m，最大厚度约893 m，面积约2 648 km²，体积约953 km³。古乡冰期时，流域内约63%的区域被冰川所覆盖，而根据第二次冰川编目统计［4］的数据，现代冰川的覆盖率约为22.4%。

3.2 古冰川ELA

冰面纵剖面模型只能模拟中流线上的冰面高程和冰川厚度，因此重建古冰川整个冰面高程时需要进行插值。本文使用了IDW、UK和OK等三种常用空间插值方法，得到了三个不同的古冰面高程分布（图6），结合AAR工具［12］和THAR法计算了相应的冰川ELA，结果显示：当采用AAR法时，古乡冰期时冰川的ELA分别为4 021 m、3 867 m、3 847 m。采用THAR法时，估算出古乡冰期时冰川ELA分别为3 720 m、3 649 m、3 649 m（表3）。从估算的结果来看，AAR法与THAR法得到的古冰川ELA相差较大，可能有以下几个方面的原因：①使用AAR法计算ELA时需要考虑冰川形状、类型和规模等特征［26］，而THAR法没有考虑冰川形状或不同谷地的面积-高程变化［34］；②采用AAR法时，可能会因为重建的古冰川表面面积不准确而产生误差；③使用THAR法时，若雪崩对冰川的积累影响较大，则会难以界定冰川的最高高程。因此，本文取两种估算方法得到的古冰川ELA平均值作为最终结果，这样能有效避免使用单一计算方法所带来的误差。

表3 波堆藏布江流域冰川ELATable 3 ELAs in the Bodui Zangbo River catchment

不同的空间插值方法得到的古冰面高程对于重建古冰川冰量、ELA等重要参数影响较大。为选择合适空间插值方法，本文在中流线上的数千个插值点中随机抽取10个点，对比其不同插值结果与模拟值（表4中的实测高程）之间的误差，结果见表4。从误差指标可以看出，IDW插值的古冰面高程值的绝对误差小于5 m，与实测值之间的相对误差在0.01%～0.1%之间。相对地，UK和OK插值的绝对误差分别可达347 m和277 m，相对误差分别在0.002%～12%和0.002%～10%之间。由此可见，IDW插值法的古冰面高程插值精度明显好于UK和OK插值法。主要原因是IDW插值法对已知高程点设置权重值，并搜索插值点与已知点之间的最短距离来进行空间插值，而UK和OK插值法要求已知高程点的密度分布较大，对于密度较小的区域，空间插值精度较低。本文选取中流线上每个点之间的间隔为200 m，密度较小，已知点较多，因此UK和OK插值法的精度要低于IDW插值法。

表4 不同空间插值方法得到的古冰面高程精度对比Table 4 Precision comparison of paleo-glacier surface elevation estimated from different spatial interpolation methods

最终选择IDW插值得到的古冰面高程，结合AAR法和THAR法计算古乡冰期时波堆藏布江流域内冰川ELA，结果取平均值3 871 m（图6和表3），相较于现代冰川ELA（4 455 m）下降了约584 m（表3）。Zhou等［5］曾对古乡冰期时波堆藏布江流域内冰川ELA进行估算，结果显示，古乡冰期时冰川ELA约为3 800 m，相较于现代冰川ELA（4 600 m）下降约800 m，本文古乡冰期时冰川ELA的平均值与此前研究之间仅相差约71 m，下降值相差约216 m。

4 结论

本文在冰川地貌外野实地考察和已有年代学为基础上，辅以高清遥感影像/卫星照片，对波堆藏布江流域古乡冰期时的冰川作用范围进行了重建；后进一步运用冰面纵剖面模型对波堆藏布江流域古乡冰期时古冰川进行了模拟；此外运用AAR和THAR方法对古乡冰期和现代冰川ELA进行了估算。古乡冰期时，波堆藏布流域冰川的平均厚度约为360 m，冰川总面积约为2 648 km²，体积约为953 km³，流域内的冰川覆盖率由古乡冰期的63%缩减至现在的22.4%；现代冰川ELA约4 455 m，古乡冰期时ELA约为3 871 m，较现代冰川下降了约584 m。

“古乡冰期”是李吉均先生主导提出的第四纪冰川重要冰期概念，谨以此文，纪念李吉均院士！

致谢：感谢华东师范大学地理科学学院许可芃在数据处理中提供了帮助。