面向6G的编码调制和波形技术*
2021-08-03刘孟孟方健袁瑞敏李双洋白宝明
刘孟孟,方健,袁瑞敏,李双洋,2,白宝明**
(1.西安电子科技大学综合业务网理论及关键技术国家重点实验室,陕西 西安 710071;2.新南威尔士大学电子工程与通信学院,澳大利亚 悉尼 2052)
0 引言
随着第五代移动通信(5G)系统进入商用化阶段,世界各国已开始部署Beyond 5G/6G技术的研究,我国也于2019年11月正式启动第六代移动通信(6G)技术研发。今年6月,IMT-2030(6G)推进组更是发布了《6G总体愿景与潜在关键技术》白皮书。6G无线通信面向2030年之后的需求,以广覆盖、全频谱、强安全、支持全应用作为愿景[1],主要技术指标包括采用更高的频段达到超高吞吐率(峰值数据速率达到Tbps)、更高的频谱效率与功率效率、更高的可靠性与更低的时延(小于1 ms)、更高的连接密度与更高的移动速度(大于800 km/h)等。面向这些指标需求,6G需要新的空口传输技术[1]。
信道编码与调制技术均是物理层关键技术。网格编码调制[2](TCM, Trellis-Coded Modulation)、多层编码[3](MLC, Multilevel Coding)和比特交织编码调制[4](BICM,Bit-Interleaved Coded Modulation)都是典型的带宽有效编码调制方案。5G系统采用BICM作为其编码调制方案,并且采用了最高达256-QAM的高阶调制[5]。未来6G需要更大带宽、更大信号星座、更多天线,以达到更高频谱效率、更高吞吐率。对于大信号星座调制系统采用何种编码调制方案达到高吞吐高可靠传输是当前的一个重要研究课题。鉴于此,本文提出了一种基于5G LDPC码的混合MLC和BICM的编码调制方案,能够在获得较好的误码率性能的同时具有较低的复杂度。
在调制波形方面,4G与5G均采用了正交频分复用(OFDM, Orthogonal Frequency Division Multiplexing)技术。在B5G/6G支持的高移动场景下,例如高速列车、V2V、无人机、卫星通信等,高速移动会产生大的多普勒频移,此时OFDM的子载波之间的正交性会遭到严重破坏,导致性能急剧恶化。如何在高移动场景下提高传输速率仍是6G未来面临的挑战。最近,Hadani等学者提出了一种面向高移动场景的新型波形技术——正交时频空(OTFS, Orthogonal Time Frequency Space)调制[6]。相较于传统的OFDM调制技术,OTFS采用了时延-多普勒域信号表示,充分利用了时延-多普勒域信道和信息符号之间耦合的不变性、可分离性以及正交性,并且具有全分集增益[7]的潜力和良好的鲁棒性。本文将面向6G中的高移动场景及高频段通信场景,讨论OTFS的峰均比(PAPR, Peak to Average Power Ratio)、分集增益和编码增益、信道均衡与信号检测算法,探讨其优势潜力以及需要进一步研究和解决的问题,为6G波形设计提供一定的思路。
1 混合MLC-BICM编码调制技术
1.1 编码调制系统组成
为了实现高谱效传输,6G系统将采用更大的信号星座。对于大信号星座,系统通常工作在较高信噪比区域。在Ungerboeck星座子集划分链的某一层,子集内星座点间的距离相对于工作信噪比已足够大,从而子集内星座点的索引比特可靠度已很高,这些比特只需要简单的编码保护(甚至不需要编码保护)就可达到很低的错误概率,不需要使用复杂的软判决强FEC码保护。我们只需要对索引子集的比特进行强力保护,这样就能够有效利用编码能力,简化编码调制系统设计,从而实现高效、高可靠、高吞吐数据传输。文献[8]针对光纤通信系统提出了一种级联编码和高阶调制相结合的方案,实现了性能与复杂度之间的良好折中。受此启发,本文将综合利用MLC和BICM的优势,采用“串行级联编码+混合MLC/BICM”的设计思路,对信号点标号比特分等级保护,在性能与复杂度之间实现较好的折中。其原理框图如图1所示:
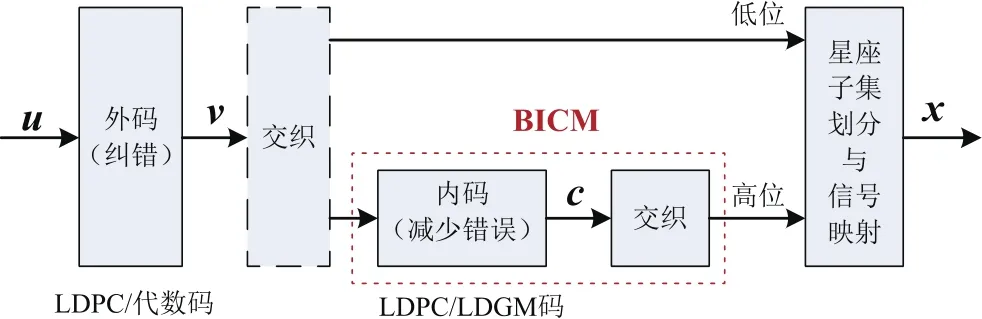
图1 “串行级联编码+混合MLC/BICM”原理框图
本文主要讨论LDPC码作为内码的混合MLC/BICM系统设计与性能,首先介绍星座子集划分与分层处理,然后介绍了信号映射,最后给出了系统仿真结果。
1.2 子集划分
子集划分是将大星座分裂成多个子星座。对子星座而言,信号点之间的欧式距离足够大,即便不进行编码保护,也能获得理想的错误概率。信道编码仅需要对星座集合进行保护。本文采用Ungerboeck子集划分方法[9]对高阶星座进行划分。对于M-QAM,M=2m,根据公式(1)[10]可以计算出第j层星座的误比特率(BER, Bit Error Rate),0≤j≤m。其中,Es表示初始星座的平均能量,Δj是第j层星座能量归一化后的最小欧氏距离,ρ是编码调制系统的频谱效率。用R表示信道编码的码率,则对于M-QAM,频谱效率ρ=R·log2M。
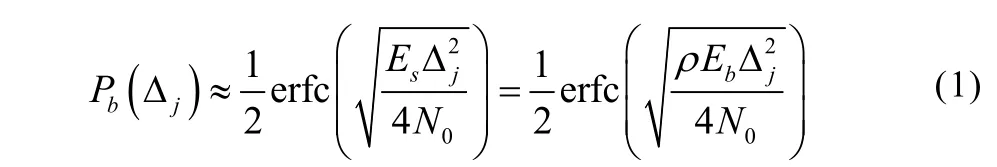
用(Eb/N0)*表示编码调制系统的最小工作信噪比,用(Eb/N0)Shannon表示Shannon容量限。在AWGN信道中,为了能够将BER降低到10-5以下,TCM方案的工作信噪比至少需要比相应频谱效率的Shannon容量限高4 dB左右。本文为了获得逼近Shannon容量限的性能,采用LDPC码编码方法,并将编码调制系统的信噪比余量设置为1 dB,即:
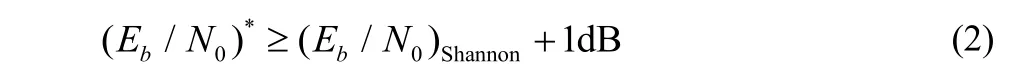
由信息理论计算可知,当频谱效率为ρ=5比特/符号时,(Eb/N0)Shannon=7.9dB。根据公式(2)计算出编码调制系统的(Eb/N0)*为8.9 dB。表1给出了在该信噪比下对64-QAM进行子集划分后各层的误比特率性能。在分析当前层的误比特率时,不考虑上一层的判决错误传播。可以看出,在划分到第4层的时候,子集内的误比特率已经低于10-5。此时,子集内包含4个信号点。因此,一个64-QAM符号中不需要进行编码保护的比特数为2。

表1 Eb/N0=8.9 dB下64-QAM各层的误比特率
1.3 信号映射

图2 4点、16点格雷映射
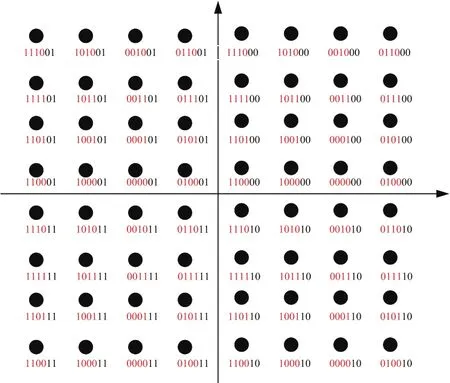
图3 64-QAM子集划分映射
1.4 系统仿真
图4给出了两种64-QAM编码调制系统的模型。图4(a)为混合MLC/BICM系统,图4(b)为BICM系统。其中,64-QAM(a)采用图3中的映射方式,64-QAM(b)采用64点的格雷映射。两个编码调制系统的频谱效率为5比特/符号。混合MLC/BICM系统的发送端是一个多层编码结构,发端的3个信息比特经过3/4码率的LDPC编码后,得到4个编码比特,这4个编码比特用于选择星座子集,另外的2个信息比特则选择子集中的信号点进行传输。混合MLC/BICM系统的接收端采用了多级译码结构。解映射器计算出编码比特的度量值,然后传递给LDPC译码器。根据LDPC译码结果得到3个被编码的信息比特,同时确定发送信号所在的子集,最后在子集中使用硬判决得到2个未编码的信息比特。对于BICM系统,LDPC码的码率为5/6。

图4 64-QAM编码调制系统模型
在进行系统仿真时,设定信息位长为2560,LDPC码为5G标准中的码,交织器采用随机交织,仿真结果如图5所示。在BER=10-5,64-QAM调制时,混合MLC/BICM系统相比于BICM系统约有0.1 dB的编码增益。图5还给出了频谱效率为7比特/符号、采用256-QAM调制的混合MLC/BICM系统和BICM系统的性能对比,其中,信息位长度仍为2562。结合公式(1)和公式(2),可以计算出256-QAM在划分到第4层的时候,子集内的误比特率低于10-5,此时,子集内包含16个信号点。因此,混合MLC/BICM系统的一个调制符号包含4个未编码比特,LDPC码的码率为3/4;对于BICM系统,LDPC码的码率为7/8。从图中可以看出,在BER=10-5,256-QAM调制时,混合MLC/BICM系统相比于BICM系统约有2.5 dB的编码增益。

图5 混合MLC/BICM和BICM系统采用64-QAM和256-QAM时的误比特率性能
2 新型波形技术——OTFS调制
面向6G中的高移动场景及毫米波等高频段通信场景,OTFS调制技术相较于OFDM调制技术,可利用二维逆辛有限傅里叶变换(ISFFT, Inverse Symplectic Finite Fourier Transform)将时延-多普勒域上的每个信息符号扩展到整个时频域平面上,使每一个传输符号都经历一个近似恒定的信道增益,具有良好的鲁棒性。本节对OTFS调制技术的基本原理进行介绍,并对其分集增益、编码增益、峰均比、信道均衡与信号检测算法等进行分析和讨论。
2.1 线性时变无线信道的描述
线性时变(LTV, Linear Time Variant)无线信道响应可用时域、频域或时延-多普勒域上的脉冲响应来描述。在高移动场景下,由于多径时延扩展以及多普勒扩展的影响,LTV信道为既有时间色散又有频率色散的双色散信道。在时间-延迟(TD, Time-Delay)域上,可用以时间t、时延τ为参数的时变脉冲响应g(t,τ)来描述其信道响应;除此之外,还可以以时间t、频率f为参数的脉冲响应H(t,f),以及以时延τ、多普勒ν为参数的脉冲响应h(t,ν)分别在时间-频率(TF,Time-Frequency)域和时延-多普勒(DD, Delay-Doppler)域上对其描述,三者之间的相互转换关系如图6所示。其中,TD域表示和TF域表示常用于经典的信号处理,而DD域表示则广泛应用于雷达和声呐领域。
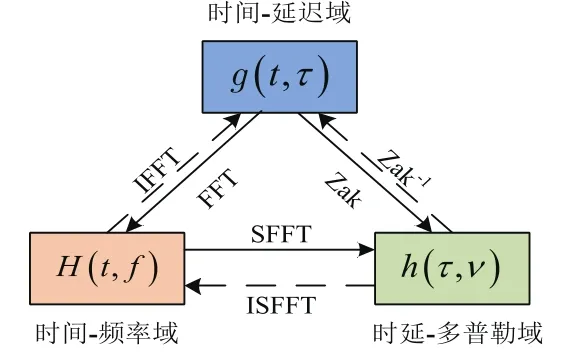
图6 信道响应在TD、TF和DD域上的表示及相互转换
信道响应在TD、TF和DD域上的相互转换涉及三对重要的变换,其中,TD域和TF域之间依赖傅里叶变换(FT,Fourier Transform)对,图中标注的是在OFDM中常用的快速傅里叶变换(FFT, Fast Fourier Transform)和其逆变换(IFFT);TD域和DD域之间依赖Zak变换对[11];TF域和DD域之间则依赖一对重要的二维变换——辛有限傅里叶变换(SFFT, Symplectic Finite Fourier Transform)。因SFFT和其逆变换ISFFT在OTFS调制中至关重要,以信道响应在TF域和DD域之间的转换为例将其表达式给出如下:
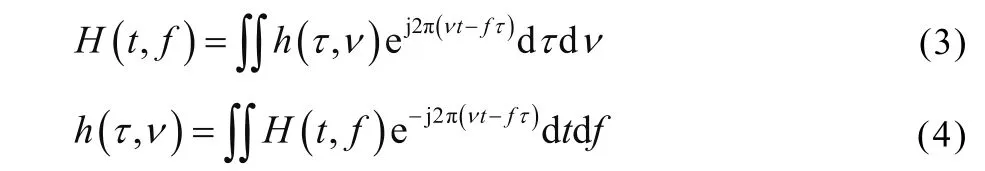
参照上述SFFT和ISFFT,便可实现传输数据信号在TF域和DD域上的相互转换。
TF域和DD域之间的相互转换也可用图7所示的二维网格图进行展示,左侧网格图为TF域网格图Λ,定义为:

图7 TF域和DD域相互转换网格图
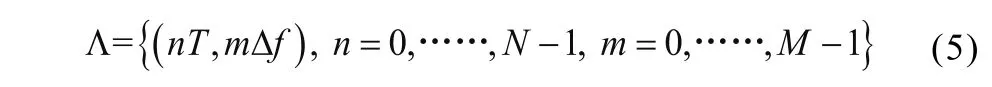
其中,T为沿时间轴t的采样间隔,Δf为沿频率轴f的采样间隔,N和M分别为沿时间轴和频率轴的采样点数。考虑多载波调制的思想,TF域网格图的表示也可以理解为一个总时长NT、总带宽MΔf的突发数据包。右侧的DD域网格图Λ⊥则定义为:
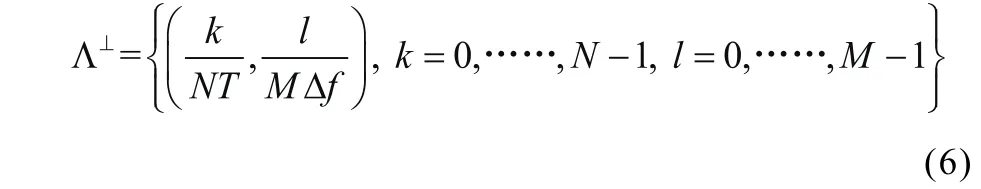
基于网格图,TF域和DD域的相互转换可以理解为,定义在TF域网格图上的信号X[n,m],0≤n≤N-1,0≤m≤M-1,经二维SFFT,映射到DD域网格图上的信 号x[k,l],0≤k≤N-1,0≤l≤M-1; 同 样, 经 二 维ISFFT,DD域网格图上的信号x[k,l]可被映射回到TF域网格图上。
2.2 OTFS调制基本原理


图8 OTFS调制技术原理框图

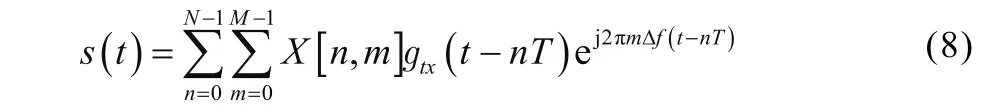
其中,gtx(t)为脉冲整形滤波器。式(8)可看作将频域调制符号映射为时域信号的OFDM调制的一般形式[12]。如上所述,对于基于OFDM的OTFS实现,OTFS调制器可以看作是一个预编码器(ISFFT)和传统OFDM调制器[13]的串联,其中OFDM调制器由一个IFFT块和一个脉冲整形滤波器gtx(t)组成。
不失一般性,LTV信道在DD域上可表示为[14]:

其中,P为路径数,hi、τi和νi分别为第i条路径的路径增益、时延扩展和多普勒频移,δ(⋅)为狄克拉函数。第i条路径的时延和多普勒频移可定义如下:
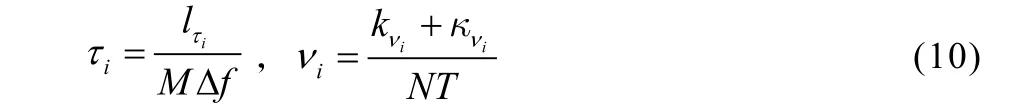
时域信号s(t)经过上述信道,接收端接收到的信号r(t)为:



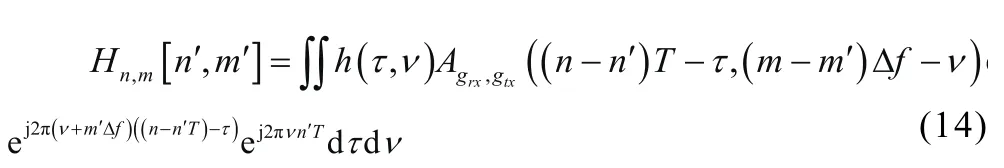

对Y[n,m]作对应的SFFT,便可得到DD域上的接收信号y[k,l],即:

其中,w[k,l]为对应的DD域噪声的采样点。
2.3 OTFS的峰均比
文献[12]指出,在上行链路中,如果给单个用户分配一个单一的多普勒频率,OTFS的PAPR就和单载波传输相同,显然低于OFDM的PAPR。此外,还指出同单载波频分多址(FDMA, Frequency Division Multiple Access)相比,OTFS可以在保持较低的PAPR的同时,获得时间和频率上的全部分集增益。随后,有学者对OTFS的PAPR进行了分析。文献[15]给出了OTFS信号的PAPR上界,并证明了其PAPR的最大值随OTFS的符号数N线性增长,而不是像OFDM等传统多载波方案那样随子载波数M线性增长,同时比较了OTFS、OFDM和广义频分复用(GFDM,Generalized Frequency Division Multiplexing)的PAPR,OTFS显然具有更好的PAPR。
对此,我们给出一个简单的关于OTFS和OFDM的PAPR比较的例子。图9所示为二者的PPAR比较结果,其中,横坐标γ为PAPR的dB形式的门限值,纵坐标Pr( P APR>γ)为OFDM或OTFS大于门限值的概率。可以从图中看出,在相同的调制方式、子载波数、符号数下,OTFS的PAPR要明显低于OFDM的PAPR。
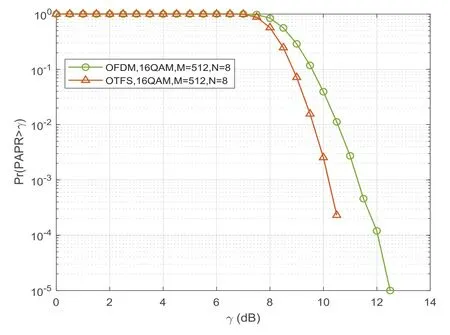
图9 OTFS和OFDM的PAPR对比
2.4 OTFS的分集增益
OTFS的一个显著优势就是具有在DD域上实现全分集增益的潜力,其与在时延或多普勒维数中可分离的多径分量的数量有关[16],例如,分集阶数为可分离路径数P。文献[7]给出了OTFS在双色散信道下实现的分集阶数的分析,指出利用相位旋转方法可以提取DD域上的全分集,同时证明了MIMO-OTFS的渐近分集阶数等于接收天线数。此外,文献[17]也表明,当OTFS帧足够长时,即使是未编码OTFS调制系统,在P=2的情况下也几乎可以获得全分集。
2.5 编码OTFS
OTFS的分集增益也为编码OTFS带来了一定的启发。文献[18]对OTFS调制的编码增益和分集增益进行了分析,发现二者之间存在着一个有趣的权衡,即OTFS系统的分集增益随着可分辨路径数P的增加而提高,而编码增益则下降。此外,在对二者分析的基础上,文献[18]揭示了信道编码参数对编码OTFS系统性能的影响,即编码改进依赖于码字对之间的欧氏距离,增加码字对之间的欧氏距离,一般可以改善编码OTFS系统的误码性能,这就衍生出了一个编码设计准则,即令所有码字对之间的最小欧氏距离最大化,而这类似于加性高斯白噪声信道的编码设计。
图10所示为以误帧率(FER, Frame Error Rate)为性能衡量标准的分集和和编码增益的权衡关系,其中,OTFS的符号数N=8,子载波数M=16,移动速度为250 km/h,编码OTFS所使用的信道编码方式为生成矩阵为[1+D,D]、码率1/2的卷积码。从图中可以清楚地看出,与P=2的情况相比,P=4时的OTFS系统有更好的分集增益,但编码增益要相对小得多。
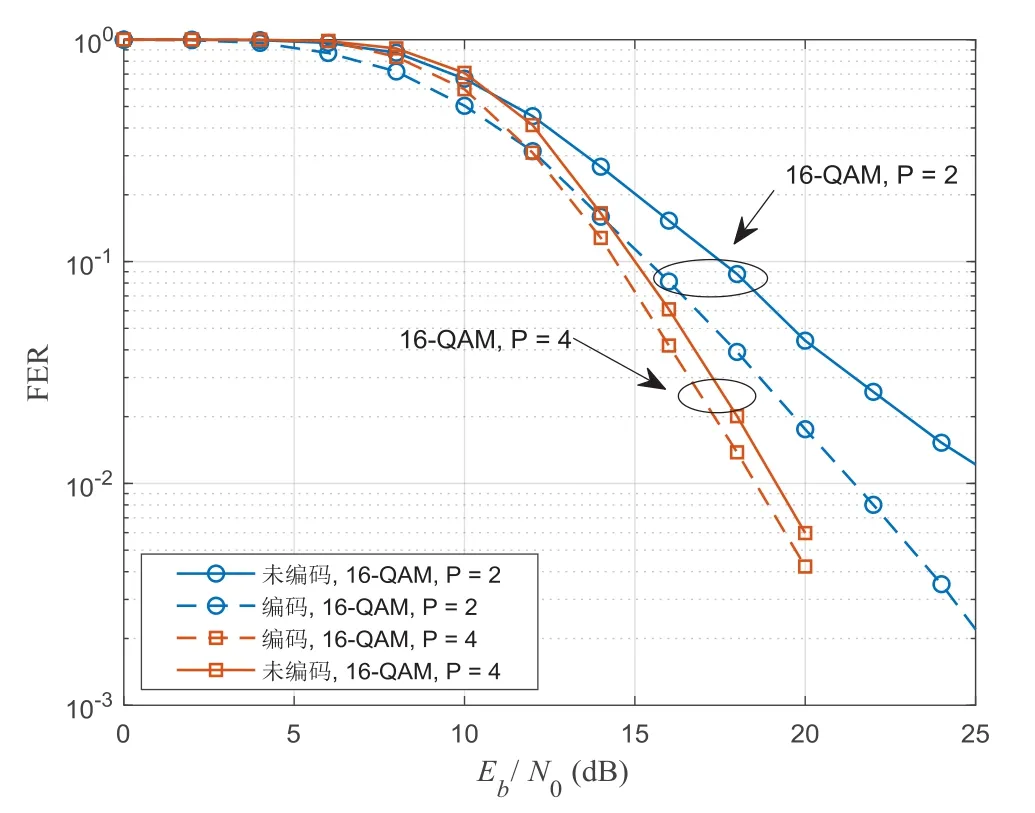
图10 不同路径下的编码和未编码OTFS系统的FER性能对比

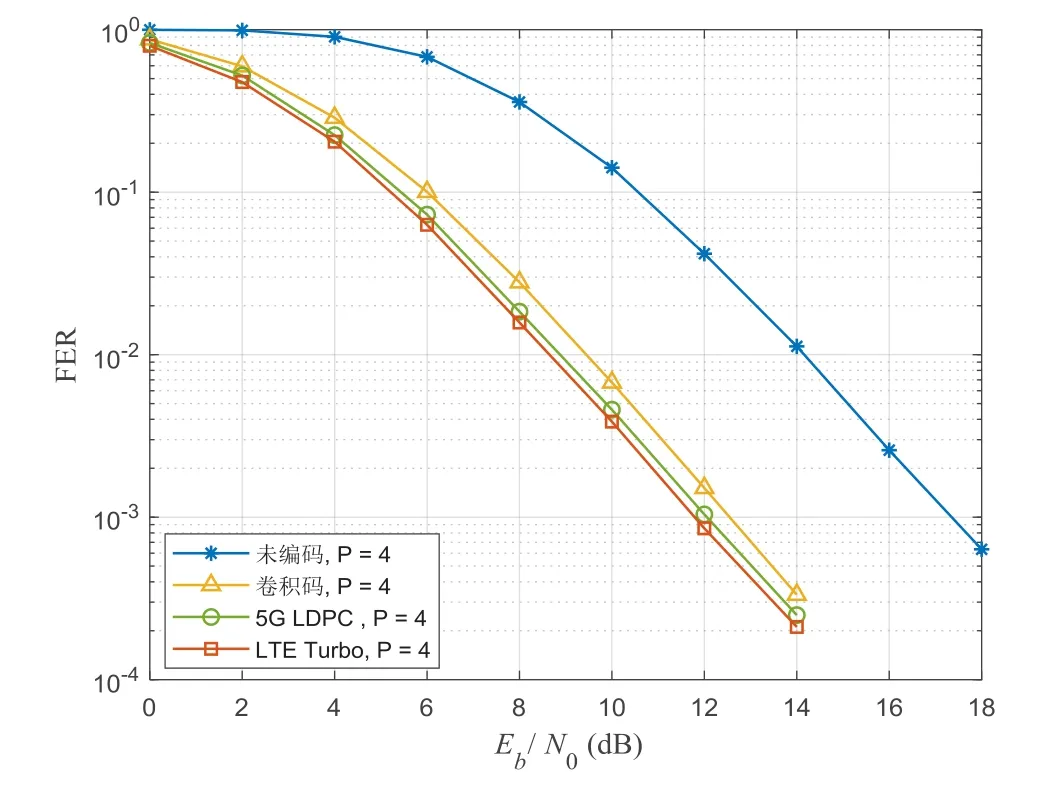
图11 不同编码方案下OTFS系统的FER性能对比
2.6 信道均衡与信号检测
在高移动情况下,即使是在短时间内,信道状态信息也会剧烈变化,这就为信道均衡与信号检测带来了巨大的挑战。对OTFS而言,其DD域上信道的稀疏性为均衡与检测带来了特有的优势。文献[19]给出了对于OTFS调制系统的嵌入式导频辅助信道估计方案,在时延-多普勒网格平面上巧妙地对导频、保护符号和数据符号进行适当排列,有效避免接收端导频和数据符号之间的干扰,使得信道估计和数据检测都在相同的OTFS帧内以最小的开销执行。此外,由于DD域的信道稀疏性和准平稳性[20],OTFS系统的信道估计性能普遍优于OFDM系统。然而,DD域信道可能并不总是稀疏,特别是在存在分数多普勒[14]的情况下,此时,导频符号周围需要更大的保护空间来放置保护符号,以避免未知数据符号对信道估计造成的干扰,这就增加了训练开销[20]。一个有效的解决方案就是通过应用TF域窗口来增强信道稀疏性,文献[21]就提出在OTFS发射机或接收机处应用一个道尔-切比雪夫(DC, Dolph-Chebyshev)窗口来抑制信道扩展,与传统的矩形窗口[19]相比,DC加窗大大提高了信道估计精度。
除了对信道估计进行分析讨论,关于OTFS信号的检测也有很多研究工作。文献[14]引入了基于最大后验(MAP, Maximum a Posteriori )检测准则的消息传递算法(MPA, Message Passing Algorithm)对DD域上的信号进行检测,它将来自其他信息符号的干扰作为高斯变量处理,以降低检测复杂度。然而,由于概率图形模型的周期较短,其所提出的MPA可能无法收敛从而导致性能退化。
为了解决这一问题,文献[22]给出了一种基于变分贝叶斯(VB, Variational Bayes)框架的收敛保护接收机,利用相对熵来近似最优检测对应的后验分布,从而在一个简单的图形模型上实现MPA。此外,基于MAP,文献[23]提出了一种混合检测方案,即根据信道系数综合考虑MAP和并行干扰抵消(PIC, Parallel Interference Cancellation),可以接近基于符号的最优MAP检测的性能。图12所示为文献[14]中提出的MPA、文献[22]提出的VB算法、文献[23]提出的混合MAP和PIC(Hybrid-MAP-PIC)算法,以及近似最优的逐符号MAP(Symbol-wise MAP)算法下的未编码OTFS系统的误比特率性能比较,其中OTFS的符号数N=100,子载波数M=150,QPSK调制,路径数P=4,最大时延索引系数为10,最大多普勒索引系数为6,算法最大迭代次数为10,从图中可以看出,阻尼因子(Damping Factor)为0.7时的MPA性能接近VB算法下的性能,Hybrid-MAP-PIC算法的性能随着子集大小L[23]的增加不断提高,逐渐逼近于近似最优的逐符号MAP算法的性能。
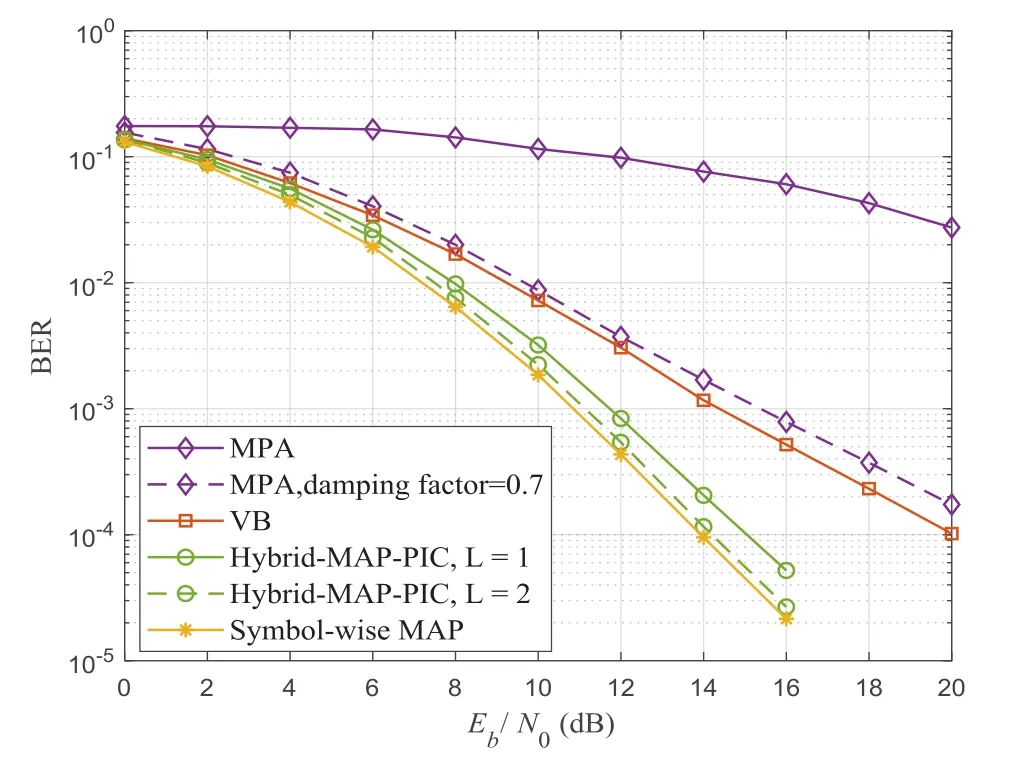
图12 不同检测算法下的未编码OTFS系统性能对比
除了在单个某个域上进行检测外,跨域迭代检测(CDID,Cross-Domain Iterative Detection)算法是一种新颖的检测方案[24],其考虑在时域采用线性最小均方误差(L-MMSE,Linear Minimum Mean Squared Error)估计,在DD域采用逐符号检测器,通过酉变换在时域和DD域之间传递外信息,同时利用时域信道稀疏性和DD域符号星座约束,在大大减少计算复杂度的情况下获得接近最优检测的性能。有趣的是,通过结合这两种基本方法,该算法即使在非常严重和复杂的分数多普勒情况下也显示出良好的误码性能。
3 结束语
面向6G核心技术指标,本文提出了一种基于LDPC码的混合MLC和BICM技术的编码调制方案。相较于5G标准中的BICM系统,本文提出的方案具有误码率性能更好、复杂度更低的优点,而且对于大星座,这种优势更为明显。此外,64-QAM和256-QAM在划分到第4层的时候,子集内的错误比特率均能满足需求。这意味着,在不改变纠错码的情况下,通过增加未经编码保护的信息比特,就可以扩展至更高阶的星座。在未来的工作中,还可以考虑选择合适的内外码以及设计更优的映射方案来提升系统性能。接着,本文对近期备受关注的OTFS调制技术进行了探讨。OTFS凭借着其优良的全分集潜力、低PAPR、良好的鲁棒性,以及时延-多普勒域信道的稀疏性,成为6G移动通信中的一种具有发展潜力的波形技术。
