基于SSP补偿和变频控制的滑环设计
2021-08-02王科瑾郝高峰
冯 新, 付 庄, 王科瑾, 郝高峰
(上海交通大学 机械系统与振动国家重点实验室, 上海 200240)
在航空航天、医疗机器人、风电等领域需要可靠性高的电能传输方法,尤其在这些设备的旋转关节中,需要克服电缆对旋转角度的束缚,因此滑环被广泛应用于旋转关节中.例如卫星运行时,步进电机通过滑环控制太阳帆板旋转,使其始终面对太阳以获得最大的照射面,然后接收到的太阳能通过滑环被传输到卫星内部[1].再如,某气象卫星通过滑环传输电力和信号并控制微波成像仪的天线旋转,从而在特定范围内接收地球表面和大气的辐射信息[2].又如,舰船在海面上航行为了获得精确的导航精度需要使用旋转惯导技术,而旋转惯导技术需要使用滑环进行电力和信号的传输[3-4].
目前,接触式滑环由于其体积小、结构简单、效率高等优点被广泛应用于上述领域.但是,接触式滑环会带来磨损、高维修性、聚积导电颗粒等缺点[5-6].因此,越来越多的学者对非接触式滑环进行了研究[7-9].文献[10]介绍了一种用于旋转超声加工的滑环,并详细地讨论了非接触式滑环的效率、最大功率以及补偿元件之间的关系.文献[11] 设计了一种用于机载雷达的滑环,并针对性地提出了滑环的设计结构.
目前,非接触滑环功率传输技术一般采用基于串联串联(SS)或串联并联(SP)补偿的电感耦合功率传输(ICPT)方案.其中,SS补偿的输出功率随负载的增大而增大,随频率的增大而减小,其具有恒流源的特性,且该补偿方案的原边补偿电容值与耦合系数无关;而SP 补偿的输出功率随负载的增大而减小,不随频率的变化而变化,其具有恒压源的特性,且该补偿方案的原边补偿电容值与耦合系数相关.这类补偿方案具有补偿结构简单的特点,但控制方案需要考虑频率分叉带来的影响,当频率方向调节错误时,严重影响系统的稳定性.
本文结合上述补偿方案的优点,提出了一种串联串联并联(SSP)补偿方案,即原边串联补偿,副边串联和并联同时补偿.该补偿方式在谐振频率处具有增益交点固定和阻抗角为0的特点.此外,提出了基于汉宁窗快速Fourier变换(FFT)的相位差检测方法,提高了抗干扰能力,避免了硬件性能的限制.改进的比例积分微分(PID)算法,根据相位差以及临界品质因数,可使系统快速稳定于零相角状态,从而减少系统的无功功率,提高系统的效率.最后,设计了一款通用的非接触滑环原型机对上述方法进行验证.
1 滑环功率传输原理及其关键技术
1.1 整体设计
通用非接触滑环的机械结构设计如图1(a)所示.该滑环系统主要由驱动电机、滑环本体、旋转平台和负载四部分组成.滑环本体由转子和定子两部分组成;驱动电机控制滑环的转子按照一定的规律进行旋转;旋转平台一端连接滑环本体的转子,随转子旋转,另一端用于固定负载.滑环本体类似于旋转变压器,是实现功率非接触传输的核心部件.其电气原理图如图1(b)所示.
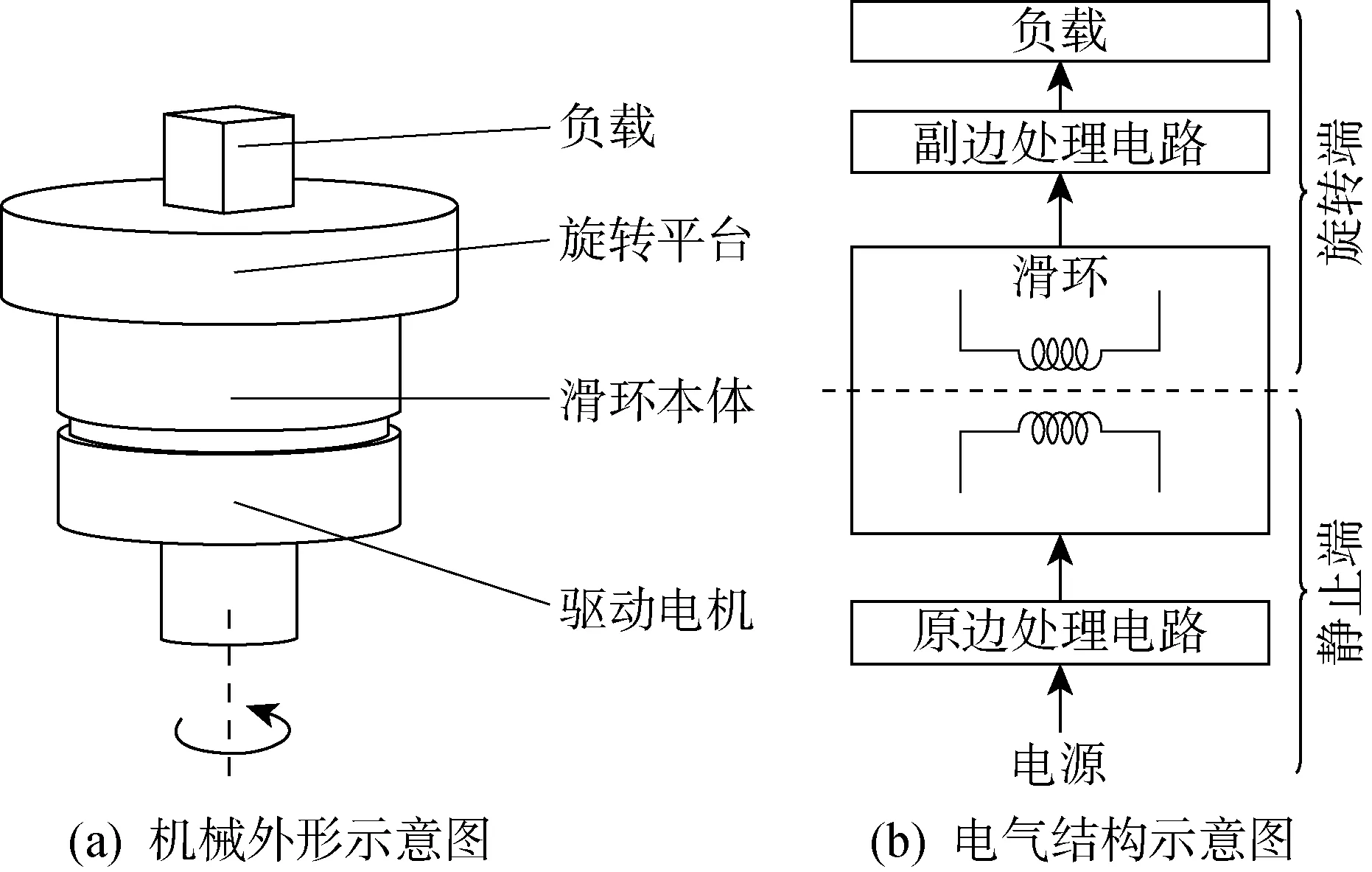
图1 非接触滑环机械和电气结构示意图
由图1(b)可知,外部的直流电逆变成两路互补对称的交流信号,施加到滑环定子绕组的两端.此时,副边绕组两端感应出相应的交流信号,并将该交流信号进行整流,可为负载提供电力[12].基于法拉第电磁感应的传输技术,使电力从接触传输变为非接触传输成为可能.
1.2 非接触式功率传输原理
根据某气象卫星旋转关节滑环设计需求所研制的一种通用非接触滑环样机,其详细的功率传输原理图如图2所示.其中:C1、C2、C3为补偿电容;RL为整流、滤波和实际负载的等效负载电阻;ADC为模拟数字转换器;DSP为数字信号处理器;I/O为输入输出端口;DC为直流信号;S1+、S1-、S2+、S2-为四路控制信号.系统的输入电压为直流28 V,该直流通过全桥逆变传输给变压器.由于该变压器存在气隙以便于转子的旋转,所以在该变压器的两端会存在一定的漏感.在实际的传输过程中,漏感会严重降低效率,也会使功率的传输变得不稳定,进而难以控制,因此需要对漏感进行补偿.目前,比较常见的补偿方式为 SS 补偿和SP 补偿[10,13-14].基于上述补偿原理,提出一种改进的SSP(ISSP)补偿方案,该补偿方案同时对变压器两侧的漏感和励磁电感进行谐振补偿,补偿后的变压器在基波频率下可相当于一个理想变压器,具有固定增益的优点.同时,从电源端看,系统的输入相角为0,减少了系统无功功率的损耗,从而进一步提高了效率.然而,随着系统温度的变化,以及电路寄生参数等原因,系统的零相角是无法实时保证的.传统的控制方式为锁相环(PLL)控制,但锁相控制设计复杂,具有一定的相位延时,对占空比有一定的要求,在多谐振频率点时会出现失控问题.为克服上述缺点,本文提出一种新型相位差检测与变频控制方法.该变频控制技术利用模拟数字转换器检测原边电压和电流,再通过数字信号处理器检测电压和电流的相位差,进而改变系统的控制频率,即改变四路控制信号S1+、S1-、S2+、S2-,以达到系统的零相角状态.所提相位差检测技术,为基于汉宁窗的FFT相位差检测技术,可避免传统过零检测速度慢、易受干扰等缺点的影响.此外,图2中的DC/DC转换器用于给芯片提供合适的电源,输入/输出(I/O)属于通信接口.
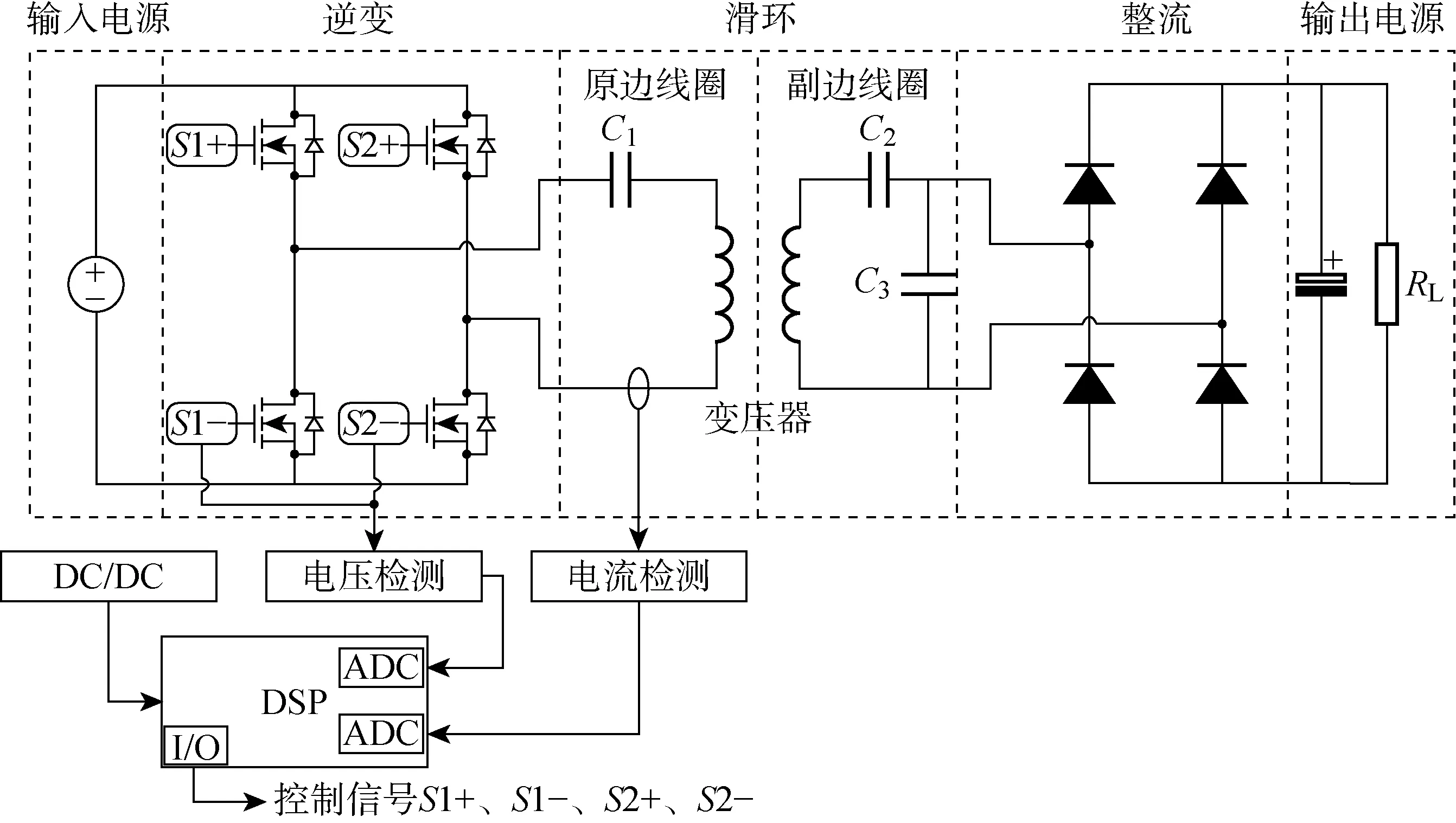
图2 非接触滑环功率传输原理图
2 功率传输模型及 SSP 补偿分析
根据文献[15],一般松耦合变压器的等效模型如图3所示.其中:U1、U2分别为直流电源经过全桥逆变后的等效交流电压和副边输出电压;I1、I2分别为原边和副边主电流;Ll1、Ll2分别为原边和副边的漏感;Lm为变压器励磁电感;N1、N2分别为原边和副边线圈的匝数.
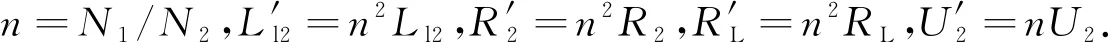
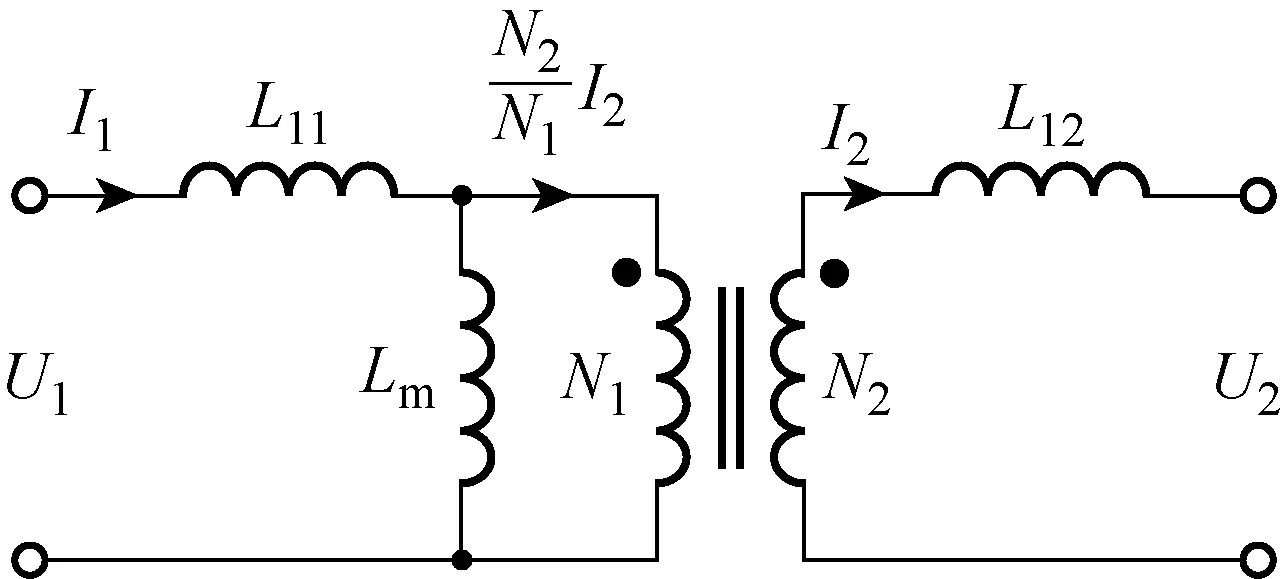
图3 变压器等效模型
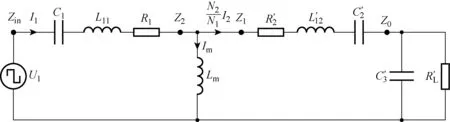
图4 SSP 补偿后的松耦合变压器等效模型
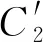
(1)
对上述模型进行阻抗分析,则有:
(2)
式中:ω为工作角频率.
进而,SSP补偿后松耦合变压器的输入阻抗为
(3)
进一步可求得系统的输出增益为
(4)
输入负载阻抗角φ可表示为
(5)
为研究SSP补偿后的频率特性,需要将漏感模型和互感模型进行转化,根据文献[17],则有:
(6)
式中:M为互感系数.
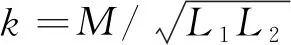
工况一设耦合系数k=0.7,可得到在不同品质因数Q2情况下,增益Gv和负载阻抗角φ随归一化频率μ的变化如图5 和6所示.
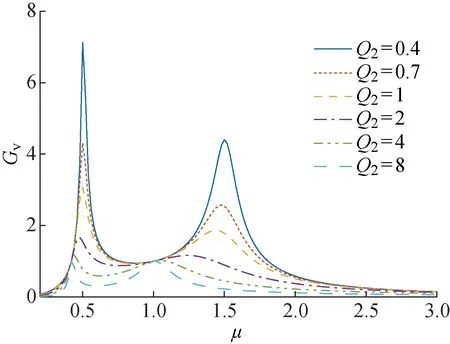
图5 工况一下的Gv
由图5和图6可知,当品质因数Q2越大,系统在频率范围内的增益Gv变化越缓慢,在μ=1左右侧的一段范围内,不同的品质因数Q2对应的系统的阻抗特性相反.
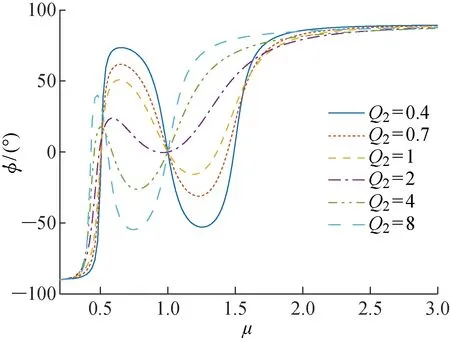
图6 工况一下的φ
工况二设品质因数Q2=0.4,得到在不同k的情况下,增益Gv和负载阻抗角φ随归一化频率μ的变化如图7和8所示.
由图7和图8可知,当松耦合变压器的耦合系数越大,系统的零相角位置相差越远,从而有利于系统的变频控制.
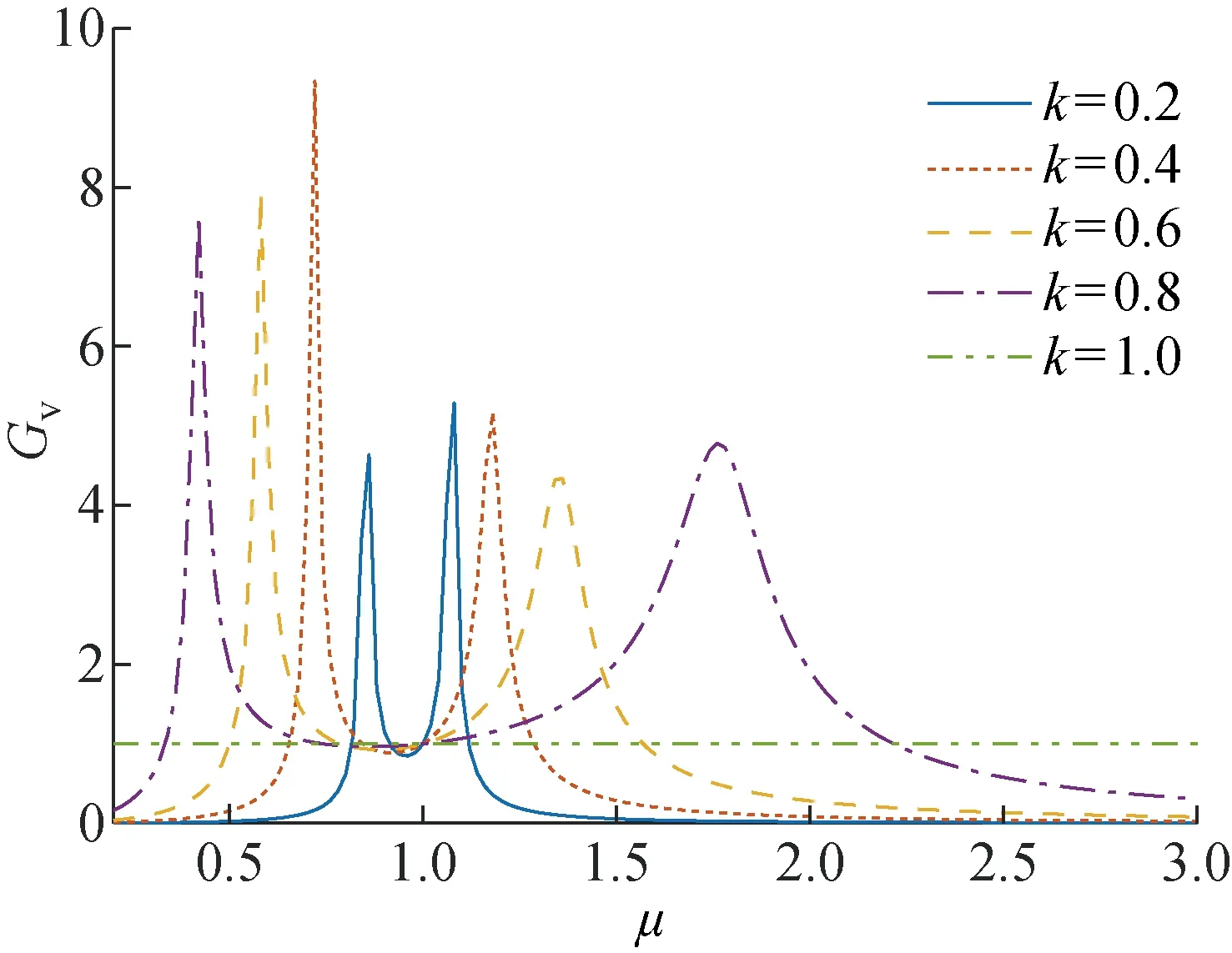
图7 工况二下的Gv
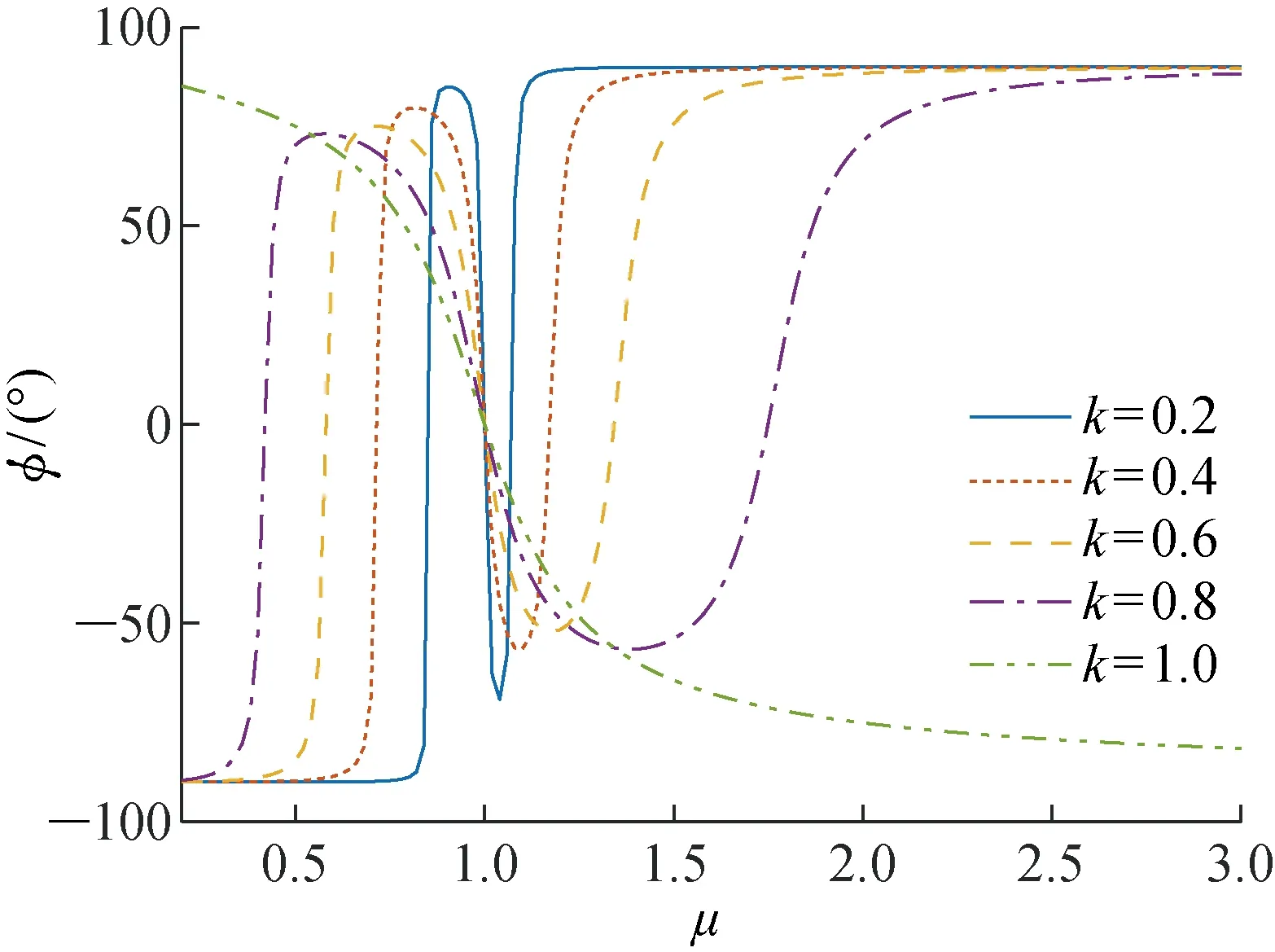
图8 工况二下的φ
此外,通过图5~8可以得出,除k=1时,系统都存在多个阻抗角为0的情况,即基于SSP补偿的方法不像SS补偿或SP补偿那样,会存在频率分叉的临界交点(即当满足临界交点范围内,只有一个阻抗角为0的情况存在).但是基于SSP的补偿方法在μ=1时,会有一个恒定的交点,且在这个交点处的增益为固定值,使系统不受耦合系数以及负载变化的影响.
3 变频控制方法
3.1 元器件灵敏度分析
由于滑环并不是完全意义的松耦合变压器,现有的制造工艺完全可以保证耦合系数k工作在一个强耦合模式(即k=0.5~1 ),并使其保持稳定.设置合适的工作频率,并根据测量的变压器参数,可计算出3个补偿电容的大小.在理想情况下,变压器的参数都不发生变化,当使用恒频控制时,补偿后的系统等效于理想变压器,输出稳定.但当这些元器件由于寄生参数、温升、误差等原因而改变其值的大小时,恒频控制会产生新的无功功率,从而降低传递效率.
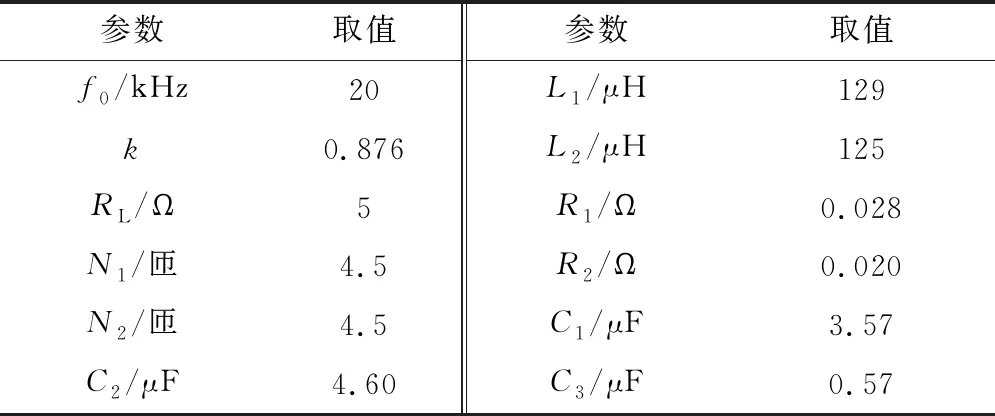
谐振频率下的仿真参数如表1所示,其中f0为谐振频率.为了研究这些元器件参数的灵敏度,对表1参数下的系统进行仿真.假设k和RL不发生变化,其他元器件参数分别变化±1%时,对应的增益和负载相位角随频率变化的曲线如图9(a)~9(d)所示,此时为到达新的谐振状态,对应的频率改变值如表2所示.其中:D为改变程度;Δf为变化频率.
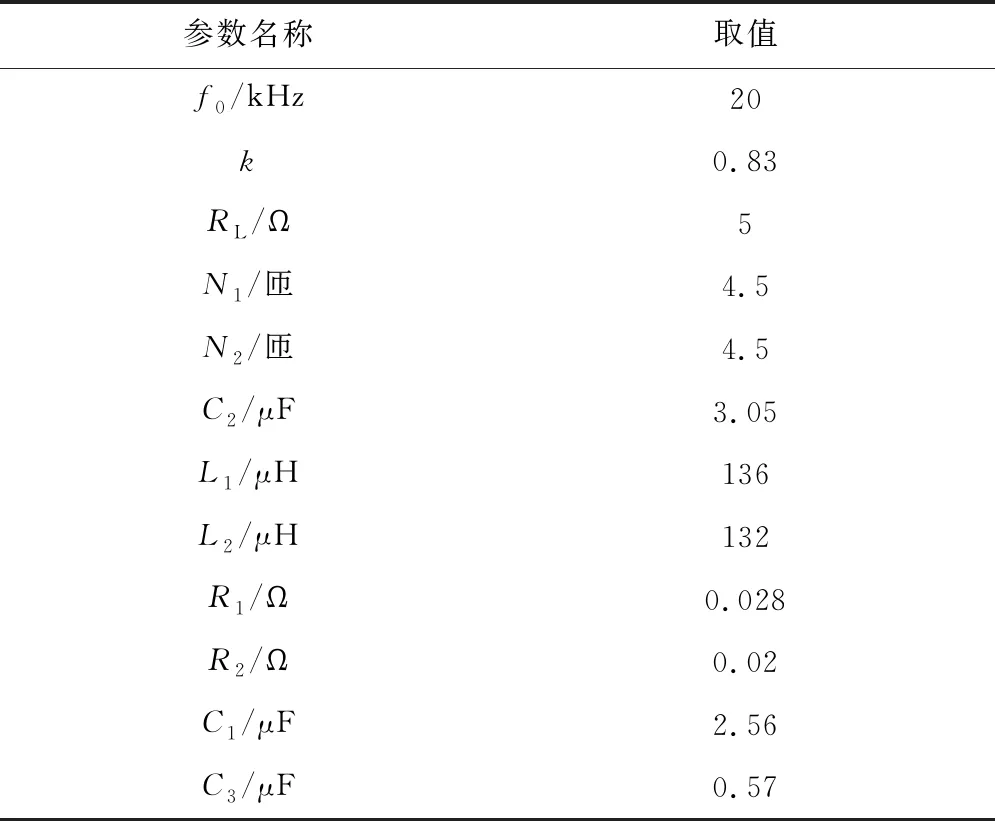
表1 谐振频率下的仿真参数
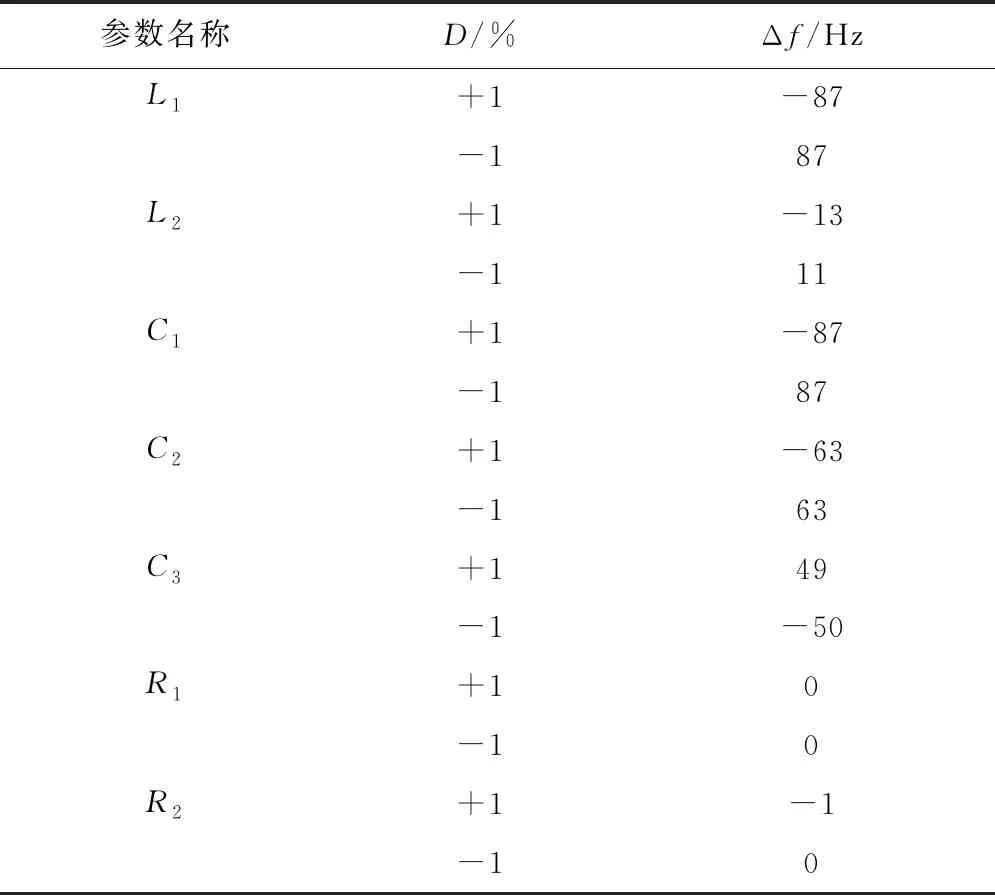
表2 参数变化1% 时对应的Δf
从表2中可以得出,当系统参数变化±1%时,对应的频率改变不超过90 Hz.原副边绕组内阻的变化对原谐振频率影响较小,而感性元件和容性元件对原谐振频率的影响较大.
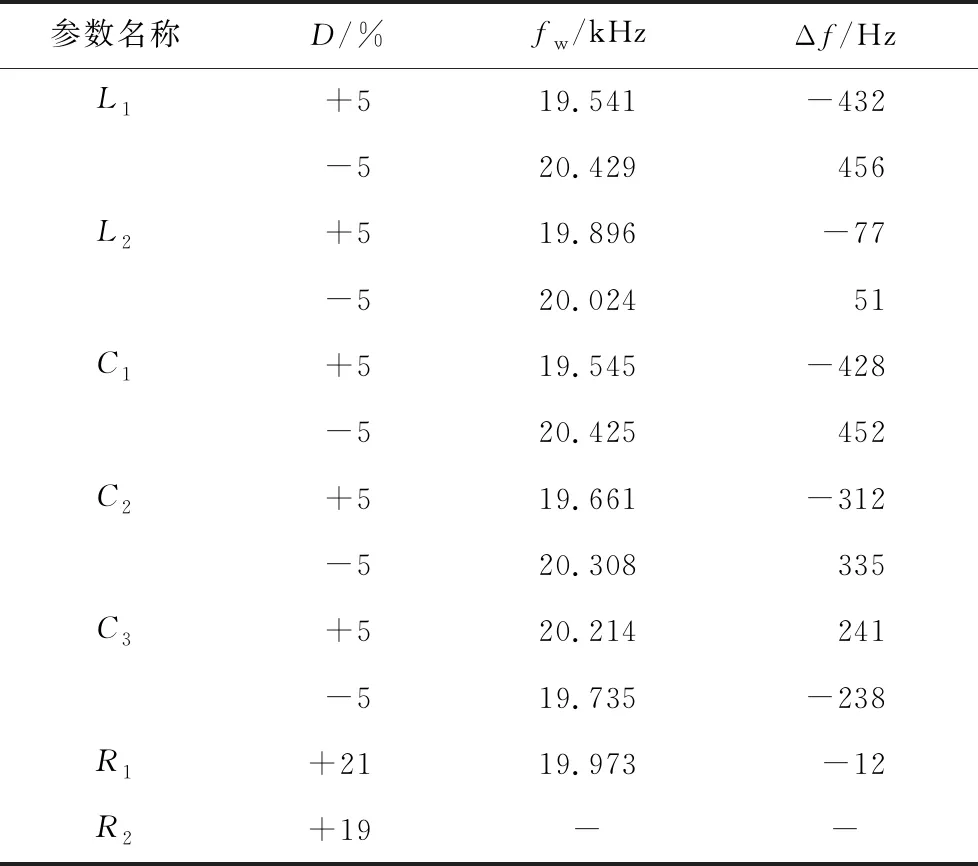
考虑极端情况,设内阻变化为±21%,其他参数最大变化程度为±5%时,对应的增益和负载相位角随频率变化的曲线如图9(e)~9(h)所示,此时为到达新的谐振状态,对应的谐振频率改变值如表3所示.
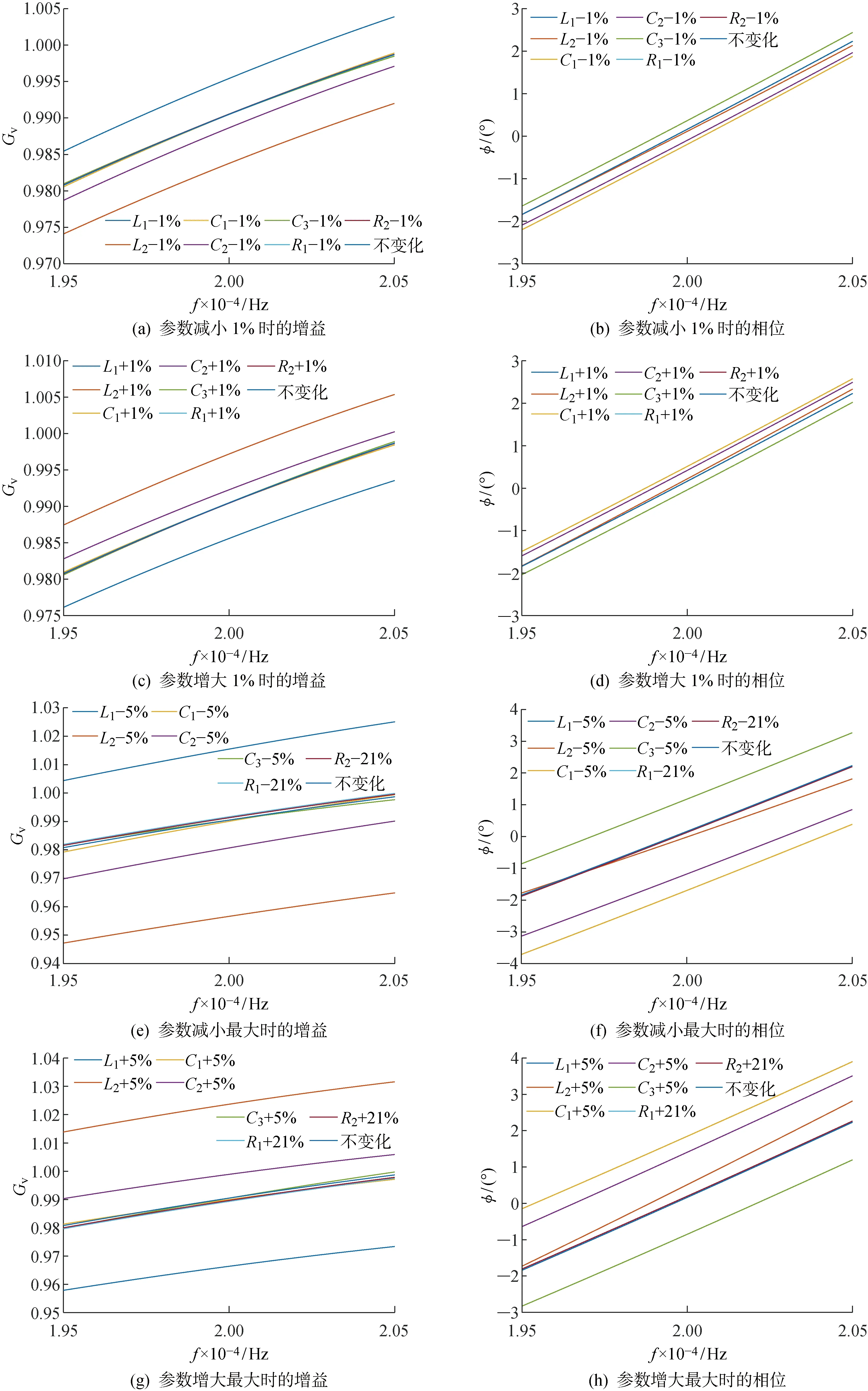
图9 不同参数变化程度对应的Gv和φ
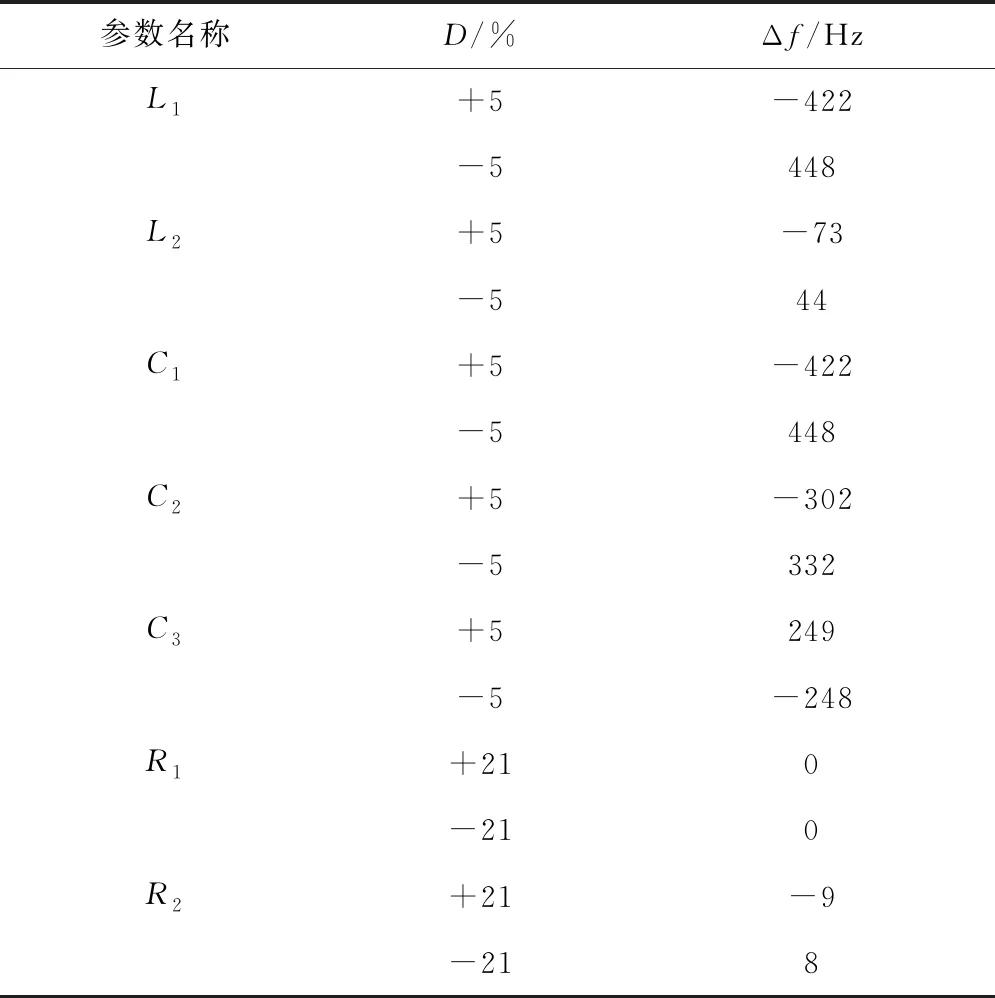
表3 参数变化最大时对应的Δf
从表3中可以得出,当系统参数变化最大时,对应的频率改变不超过450 Hz,其他结论和表2得出的结论类似.因此,选择合适的相位差检测方法对等效交流输入电压和原边电流的相位进行检测,再根据检测的相位差来调节系统的工作频率,以达到零相角状态,减少无功功率的影响.
3.2 基于汉宁窗的相位差检测方法
常用的相位差检测技术主要包括基于硬件和基于软件的检测技术.基于硬件的相位差检测技术由于受到模拟硬件器件的限制,灵活性较差等原因,适用于低精度检测的设计要求.而基于软件的相位差检测技术,首先通过同步采集芯片对被测信号进行采集,再进行数字量化等处理,从而获得相位信息[18].这种检测方法因精度较高、抗噪能力较强,而被用于对输入电压和电流信号进行采集分析.
根据文献[19],设电压和电流信号分别为
(7)
式中:φ1、φ2分别为两路信号的初始相位,且φ1,φ2∈[-π/2,π/2];A1、A2分别为两路信号的幅度;fp为两路信号的频率.
在同一时刻使用相同的采样频率fs对两路信号x1(t)、x2(t)进行采样,得到两路离散序列,即将式 (7)改写为
(8)
b=0,1,…,B-1
如果直接对式 (8)进行B点有限长序列FFT变换,则需要保证严格的整周期采样和信号周期恒定.在滑环系统中,信号是无限长序列,在进行FFT变换时,需要将无限长信号截断成有限长序列,再对此序列进行周期延拓,如果采用非整周期采样,就不可避免地造成频谱泄露和栅栏效应,继而影响相位差测量精度.此外,使用FFT测量相位差时,若信号的基波频率变化,则对相位测量值的影响较大,且误差会随着样本B的增大而增大,因此需要确保信号周期恒定.然而在滑环系统中,严格的周期采样对硬件设计较繁琐,而且变频过程中,信号的周期在小范围内是不恒定的.因此,本文通过设计汉宁窗来解决上述问题.
汉宁窗的时域表达式为
(9)
b=0,1,…,B-1
分别对式 (8)的两个信号进行相乘,以信号x1(b)进行说明,则有:
y1(b)=
(10)
将cos 展开成exp指数,并对正频率部分进行FFT变换,得到最终的离散谱表达式为
(11)
由于加汉宁窗是对信号x1(b)的时域非周期截断,即Bfs为信号1fp的非整数倍,则有:
(12)
式中:gmax为y1(b)信号频谱中最大谱线(可理解为基波频率对应的谱线),且为正整数;σ为泄露误差系数,|σ|≤0.5,当σ=0时,为对时域信号x1(b)的整周期截断.
将式(12)代入式 (11),并令g=gmax可得到最大频率的幅值和相位为
(13)
当B≫1时,式(13)可改写为
y1(gmax)=D(gmax)ej(φ1+πσ)
(14)
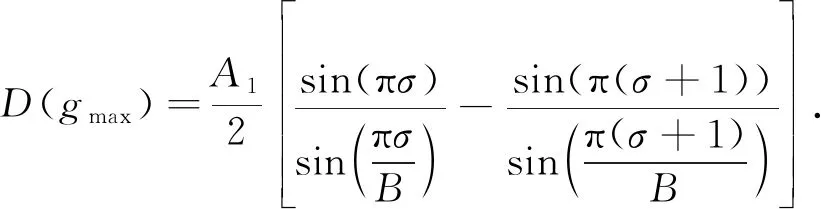
从式 (14)可以得出,y1(gmax)最大频谱对应的相位为
φ1max=φ1+πσ
(15)
同理可得信号2中,最大频谱y2(gmax)对应的相位为
φ2max=φ2+πσ
(16)
则电压和电流信号的相位差为
Δφ=φ1-φ2=φ1max-φ2max
(17)
3.3 基于零相角的变频控制方法
由图6可知,在不同的Q2下,μ=1处对应的曲线斜率并不相同,从而增大了控制的难度.品质因数Q2很小时,斜率为负;Q2很大时,斜率为正.因此,需要通过判断Q2的值,确定所需更改频率的方向,以构成闭环负反馈.
对式 (5)求μ的导数,并令
(18)
可求得不同耦合系数k下的临界品质因数Q2,0,如图10所示.

图10 不同耦合系数k下的临界品质因数
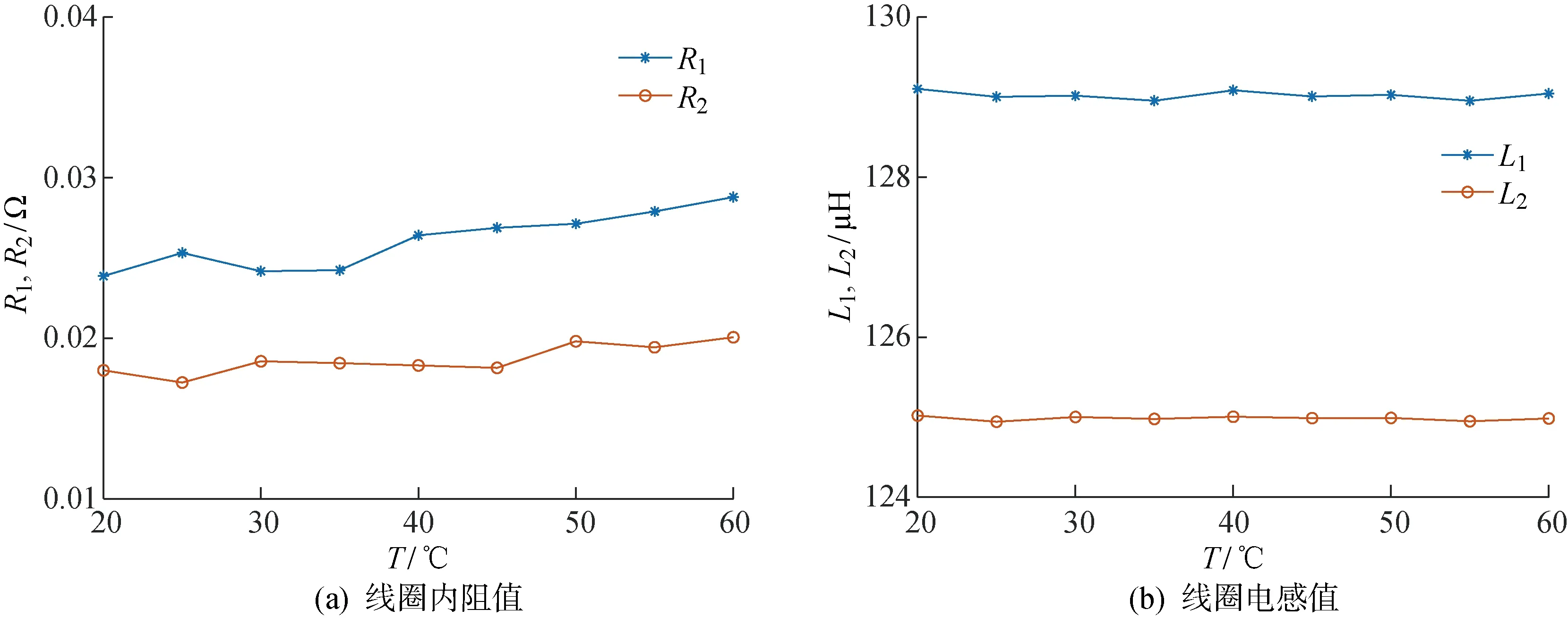
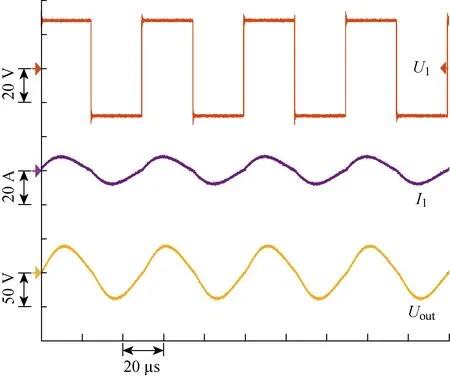
由图10可知,当实际的品质因数Q2>Q2,0时,相位角在谐振频率处的斜率为正;当Q2 图11 控制算法流程图 值得注意的是,滑环的k变化不大,因此在滑环的运行过程中,可认为Q2,0是恒定的.若在设计其他的非接触功率传递系统时,需要考虑k的变化带来的影响,在实际的控制过程中可参考文献[20]增加频率方向判断环节. 为了验证上述控制方法的可靠性,利用MATLAB软件进行了控制算法仿真,如图12所示.其中:In1为改进的PID控制器的输入;Out1为改进的PID控制器的输出. 图12 控制算法的仿真 图12中,被控对象为式(4)和(5)所涉及的模型.初始仿真参数与表1保持一致.每隔100个控制周期依次改变L1、L2、C1、C2、C3±5%的程度,所得到的阻抗角如图13所示以及对应的控制频率如图14所示.其中:t1~t10分别为L1减少5%、L1增加5%、L2减少5%、L2增加5%、C1减少5%、C1增加5%、C2减少5%、C2增加5%、C3减少5%、C3增加5%对应的时刻;考虑到和真实的变压器内阻保持一致,t11为R1增加21%的同时R2增加19%对应的时刻. 图13 输出的相位差 图14 PID 调节后的控制频率 从图13和14中可以看出,当元器件参数变化时,改进的PID控制器能使系统很快达到稳定状态,使输出阻抗角为0,从而增加了系统的效率.在稳定状态下,每组参数变化对应的频率改变值如表4所示,其中fw表示稳态频率.虽然滑环系统频率是按照20 kHz设计的,但是由于舍入误差等因素,仿真的稳态频率为19.961 kHz.这从侧面反映出在实际的滑环设计中,由于测量精度、元器件精度等原因,变压器的工作频率可能和设计频率有一定的误差,而所提变频控制方法可根据相位差自动对频率进行修正. 表4 不同D下的Δf和fw的取值变化 为验证上述理论、方法、算法的有效性,制作了一台滑环原型机,如图15所示,其中电感电容电阻(LCR)表,用于测量电感、电容、电阻的参数值.当滑环通电后,可测得原边和副边线圈对应的电感值和电阻值随温度T的变化如图16所示. 图15 基于 SSP 补偿和变频控制的非接触滑环原型机 从图16中可以看到,受温度影响较大的为线圈内阻;由于气隙的存在,原副边电感值几乎没有影响.另外,电容属于外部元器件,当选择温度系数较小的电容时,可忽略温度的影响,其值的变化主要取决于精度和寿命.当滑环达到稳定状态60 ℃时,可测得滑环系统的参数如表5所示,其中原副边线圈内阻分别增加了21%和19%. 图16 变压器参数随温度变化的测量值 表5 滑环参数 由于很难在线更改电路板元器件的大小,所以通过离线的方式,在原副边处理电路中增加或减少串并联电感和电容,对本文提出的变频控制算法进行验证.更改后的滑环参数值与表1一致.记录在以下两组工况下,PID控制器输出的系统工作频率值:① 环滑从室温到稳态60 ℃,且电感电容参数不变;② 当电容和电感分别改变±5%后,且系统分别上电后并达到稳定状态60 ℃.在这两种工况下,测得的数据如表6所示. 由表6可知,系统从室温达到稳态时的频率值从19.985 kHz变化到了19.973 kHz,原副边电阻值变化对谐振频率的影响相对较小.对比表4和6可以看出,实测的频率改变值和仿真的频率改变值基本一致,说明了该变频控制算法的正确性. 表6 不同D下的Δf和fw的实测值 系统达到稳态且参数不发生变化下,逆变电压U1(对应通道1),原边谐振电流I1(对应通道2)和输出交流电压Uout(对应通道3)的波形如图17所示.其中:3个通道的横坐标刻度为每格20 μs;通道1的纵坐标刻度为每格20 V; 通道2的纵坐标刻度为每格20 A;通道3的纵坐标刻度为每格50 V;此时对应的频率为19.973 kHz.从图17中可以看出,基于SSP补偿和变频控制的方法使非接触式滑环始终工作在零相角状态,从而减少了系统的无功功率.通过功率分析仪可得,该设计方法使系统在不补偿状态下的效率82%提升到了87%. 图17 U1、I1和Uout的实测波形图 本文根据旋转关节非接触功率传输需求设计了一款通用型非接触式滑环样机.在该滑环设计中提出用SSP补偿的方式对松耦合变压器的漏感和励磁电感等进行补偿以降低无功功率的损耗.通过理论推导,得出基于SSP补偿的变压器可使系统工作在恒定的增益下,不受负载和耦合系数变化的影响,极大地减少了频率控制的难度和复杂度. 使用基于汉宁窗的FFT的相位差检测方法可避免受硬件水平的制约,同时有效降低了系统的干扰.通过检测到的相位差,并判断系统的临界品质因数,调节PID参数以使系统始终工作在零相角状态.在该种状态下,系统受到的无功功率最小,从而提高了效率. 另外,本文只讨论了一种提高效率的方法,即如何减少无功功率.在接下来的工作中,将结合软开关等因素,对非接触式环滑功率传输进行优化升级.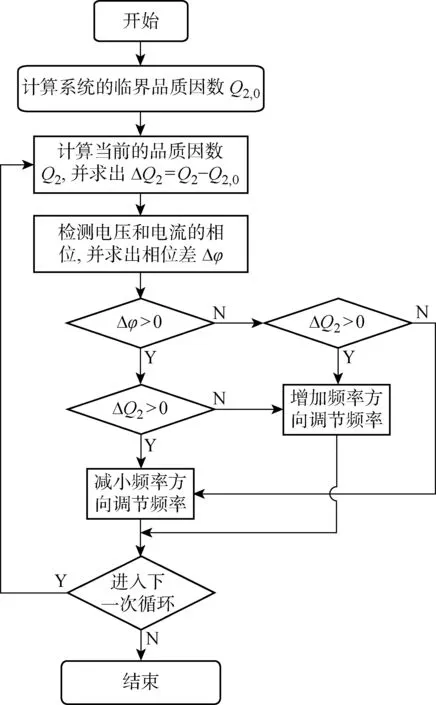
4 仿真及实验验证
4.1 控制方法仿真分析
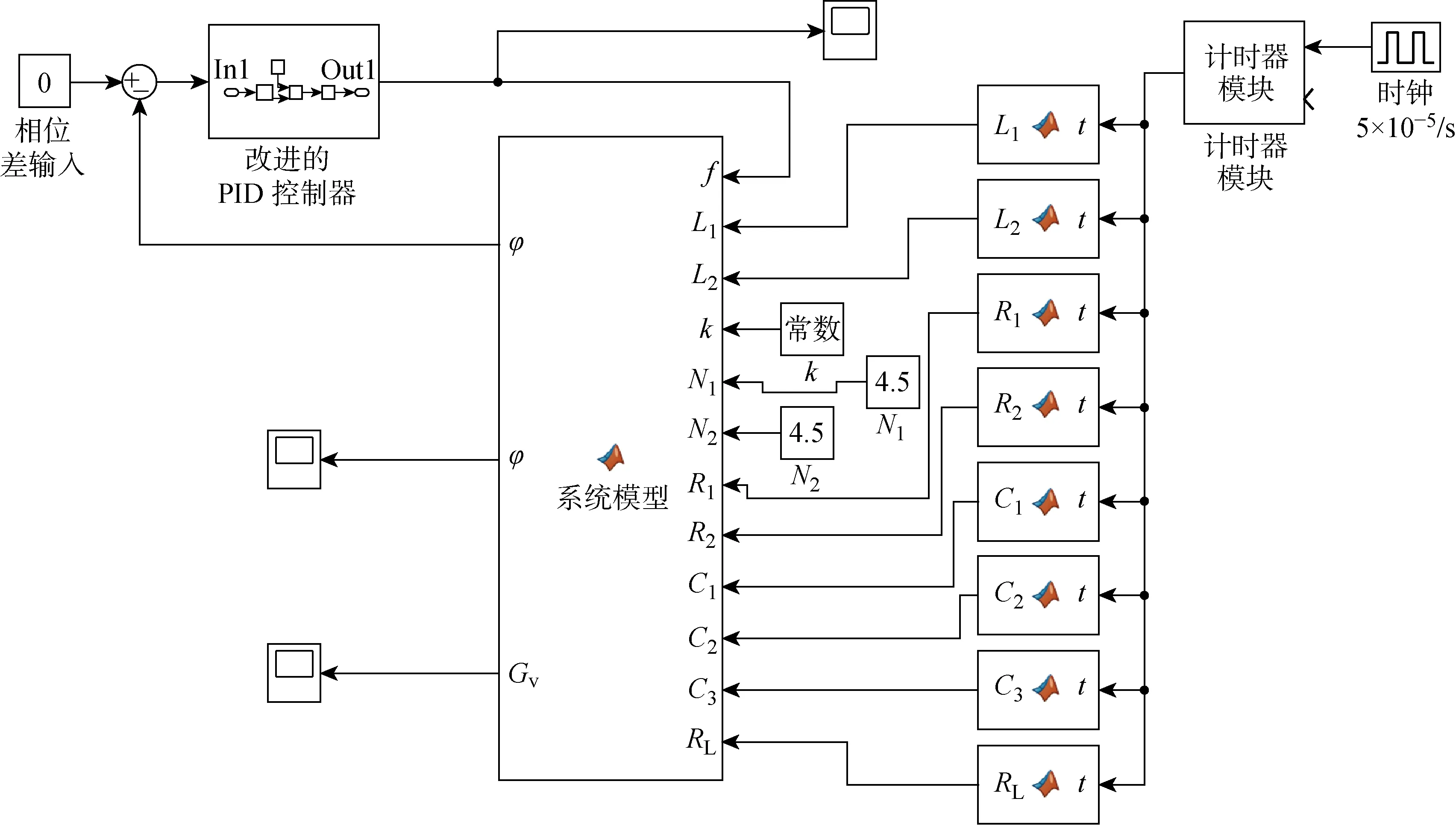
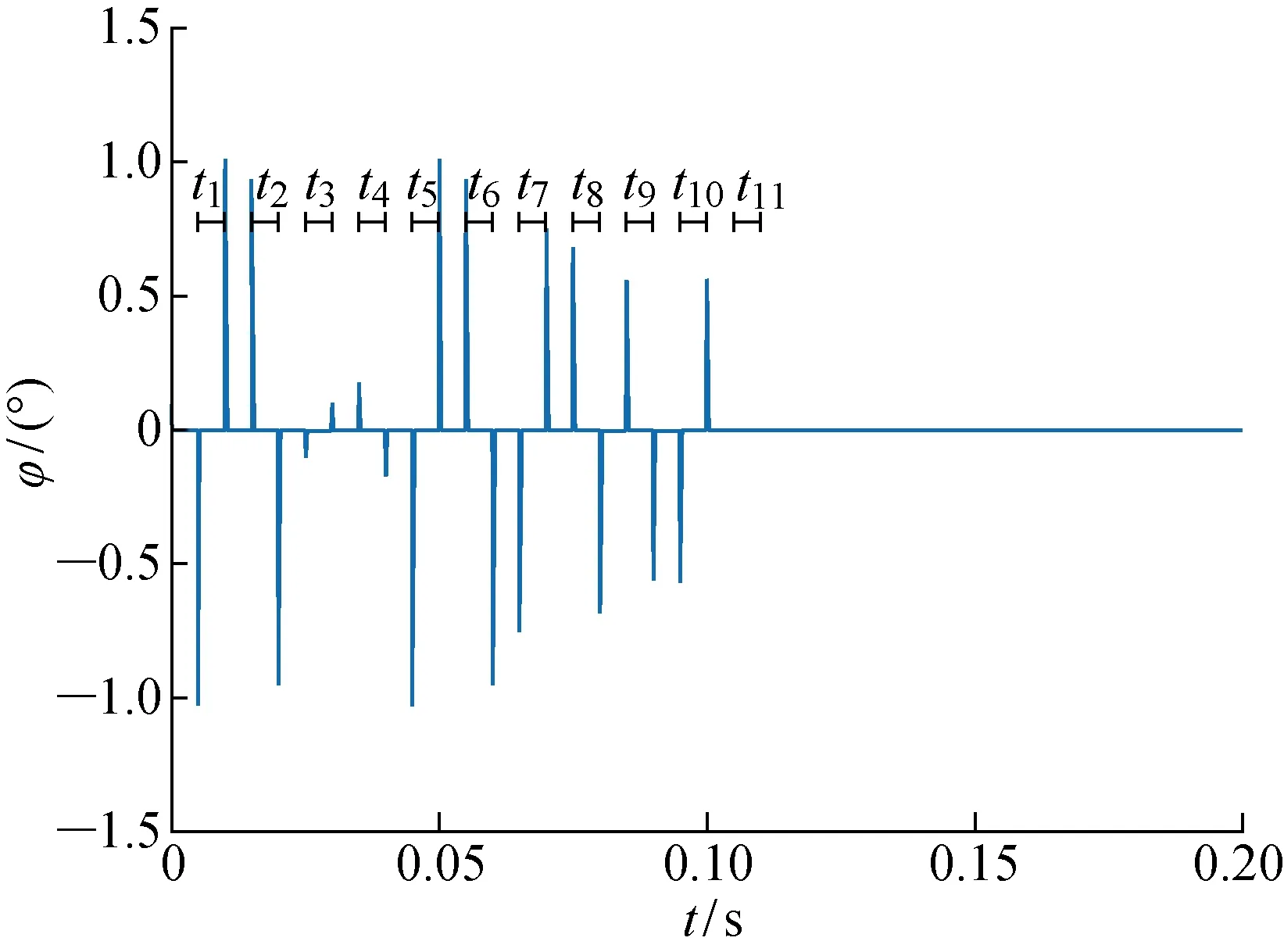
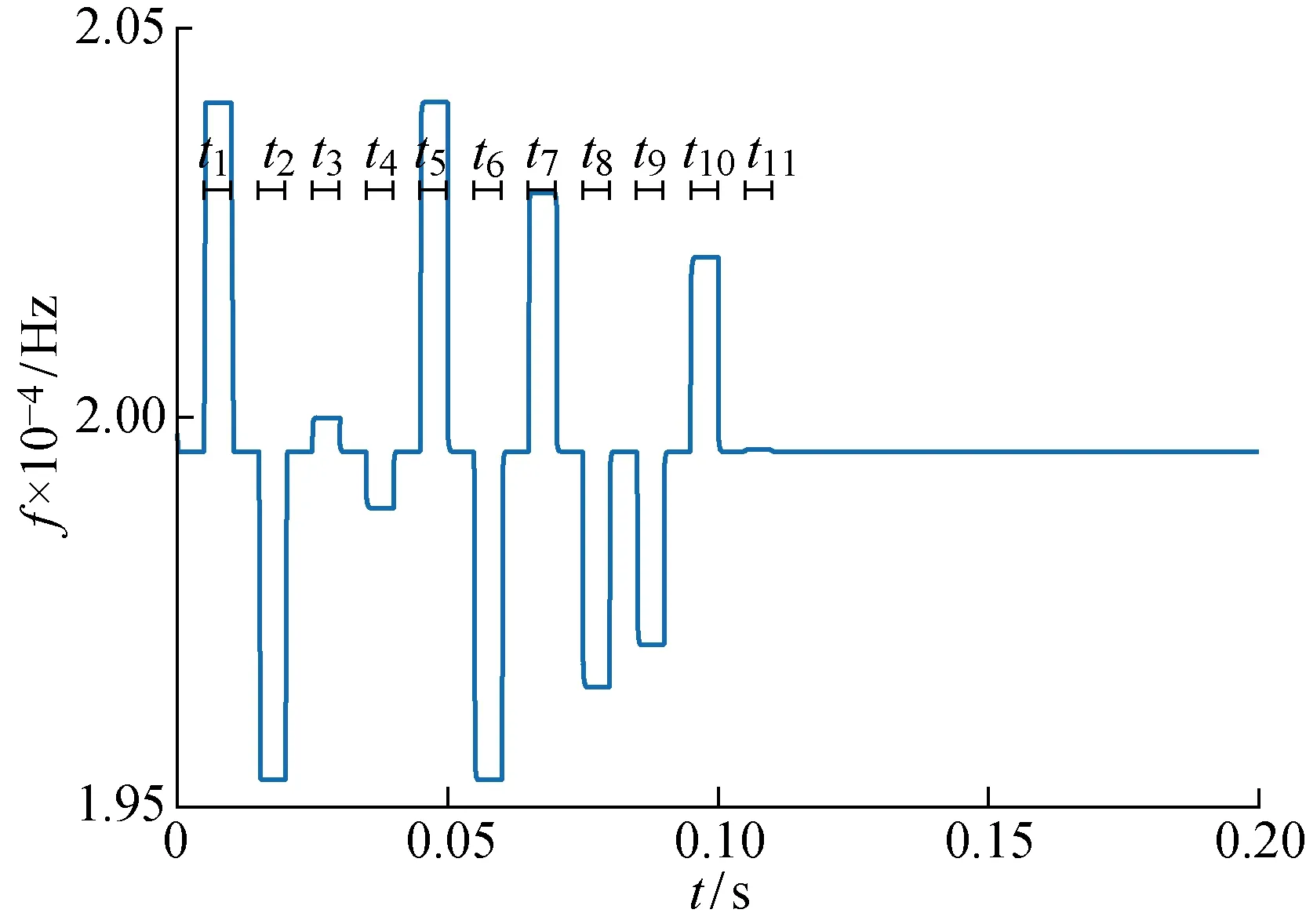

4.2 实验验证

5 结语
