基于单隐层神经网络的压电执行器非线性特征建模策略研究

盖冉翔， 汪旭东， 刘旭辉， 姚兆普

1. 北京控制工程研究所先进空间推进技术实验室， 北京 100094 2. 北京市高效能及绿色宇航推进工程技术研究中心， 北京 100094

0 引 言

压电执行器(piezoelectric actuators, PEA)是利用压电逆效应制成的一类机电驱动器，可用于精确驱动，其驱动分辨率可达到0.1 nm量级.PEA以其高精度、低能耗、高分辨率等优点而被广泛应用于各种精密仪器中.周期电压驱动是PEA的一种常见工作模式，被广泛应用于扫描探针显微镜等精密机械探测、传动装置中.然而，一些内部固有的非线性特征和外部干扰制约了PEA精度和稳定性的进一步提升.这些因素包括迟滞[1-4]、蠕变[5-7]、温度漂移[8]和高频震荡[9]等，它们相互耦合而对位移输出造成复杂的影响.其中，迟滞和蠕变属于压电材料本身取消导致的非线性，迟滞对整体的定位精度造成的干扰大概占总位移的10～15%，蠕变则有1%～5%[10].温漂和震荡属于外部干扰，它们对位移线性度的影响较小，但是会引入噪声，严重影响定位的稳定性.关于如何准确建模、辨识和补偿上述非线性特征已经成为目前的研究热点.

迟滞现象是对输出影响最显著的非线性特征.它的典型特征是输入和输出在时间上存在滞后关系，位移在周期电压驱动下会形成环状曲线，称之为“迟滞环”.动态迟滞建模的几个难点分别是频率依赖、非对称性和多非线性耦合.其中，当驱动电压频率升高时，迟滞环形状会变得更宽，在高频应用时导致很强的非线性，这称为迟滞的频率依赖或频率相关特性，如图1所示；迟滞环一般根据其行程的最高点和最低点连线对称，但在一些特殊情况下表现出非对称特征，这称为迟滞的非对称性；迟滞和蠕变、温度漂移等非线性共同存在时，不同激励电压周期所形成的迟滞环形状会发生变化，这称为多非线性耦合.以上几种特性是传统迟滞模型难以准确拟合的，同时也是当下的重点研究方向.

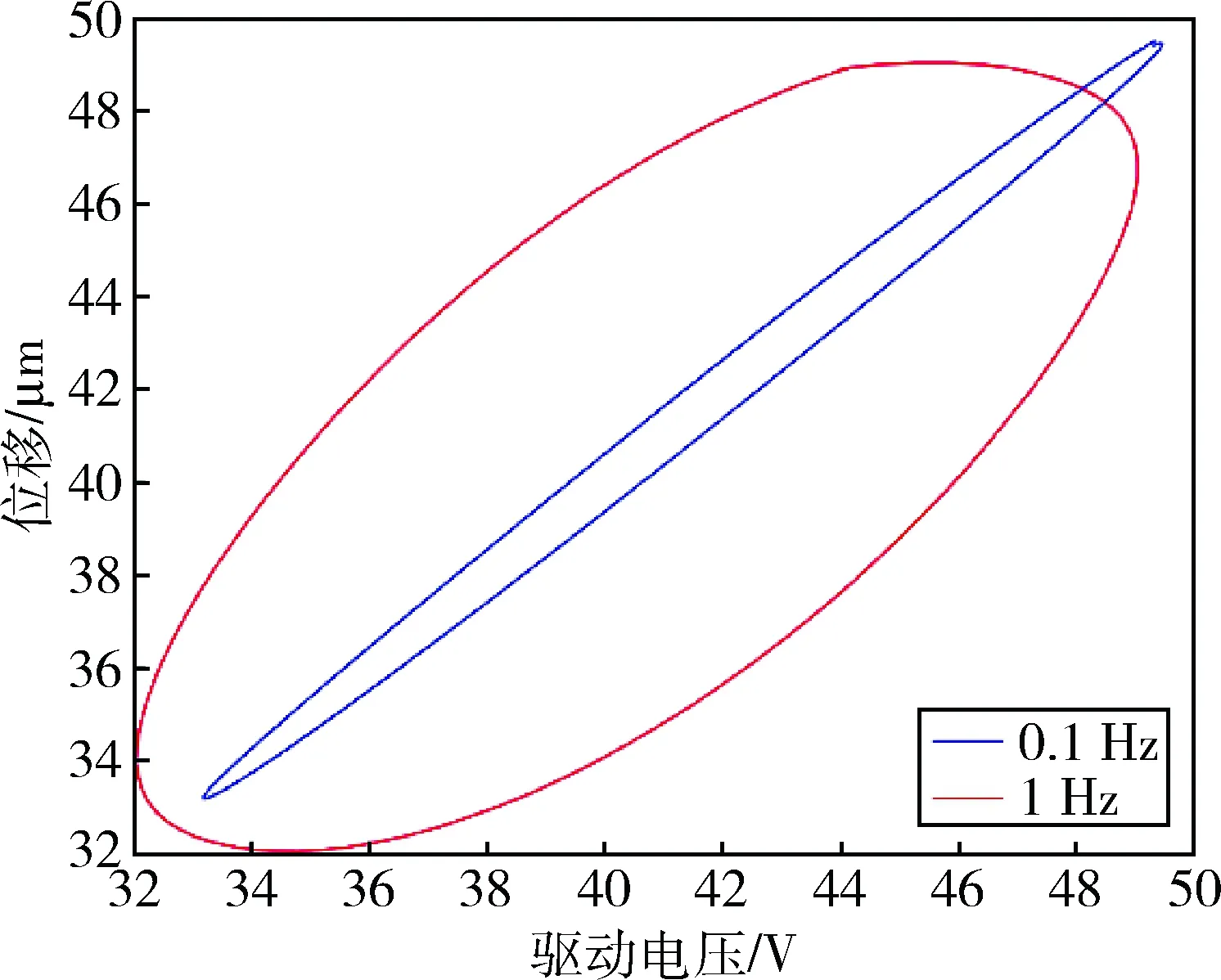
图1 不同频率激励电压下迟滞环形状对比Fig.1 Comparisons of hysteresis loops under different frequency excitation voltages

传统的迟滞数学模型有Preisach模型、Prandtl-Ishlinskii (PI)模型、Bouc-Wen (BW)模型等.WANG等[11]提出的改进式PI模型具有描述频率依赖、非对称迟滞环的能力；ZHANG等[12]利用改进式BW模型来描述非对称迟滞，并提出了一种使用粒子群优化(PSO)算法进行模型辨识的策略.ZHAO等[1]利用扩展输入空间法将迟滞转换为单值映射，并基于模糊理论完成频率依赖迟滞的建模.然而目前，针对多非线性耦合的迟滞建模存在模型庞大、数学推导复杂的问题，不便于实际应用.

蠕变现象是指在输入电压停止变化之后的很长一段时间内位移的缓慢漂移过程.典型用于表述蠕变的模型有对数时间模型和LTI模型等.LIU等[5]提出的基于分数阶理论的双对数模型成功将拟合精度提升了一个数量级左右.ZHANG等[10]通过将激励电压台阶化以求取动态蠕变，并讨论了静态和动态蠕变之间的关系.和迟滞不同的是，蠕变对于静态定位的影响更为明显，其速率和幅度强依赖于压电材料本身的特性.

温度漂移是由于压电材料的热效应而导致的非线性.对温漂现象单独建模是困难的，因为温漂几乎总是和迟滞、蠕变同时发生，难以独立分析其对位移的影响.

针对多非线性耦合的迟滞现象，本文提出了一种基于NARMAX模型的迟滞、蠕变和温度漂移的联合建模方案.其模型结构简单、推理速度快，在测试数据上的绝对误差不超过± 0.01 μm；且对于长时间范围内的漂移现象有良好的补偿和跟踪效果.

1 NARMAX模型和单隐层神经网络

NARMAX模型由Billings 最先提出，它是ARX、ARMA等线性模型的拓展，用于处理带有外源性输入的非线性数据建模，非常适合于时间序列映射的建模任务[13].NARMAX模型在非线性系统建模和辨识领域有着广泛应用.如不考虑噪声的影响，它可以用如下公式表示：

yk=Fl[yk-1,…,yk-ny,xk-d,…,xk-d-nx]

(1)

式中,yk和xk分别是模型的输出和输入，正整数nx,ny,d用来确定历史的输入和输出的数目.l代表模型的非线性度.F是需要人为确定的非线性映射.可以看出，NARMAX模型的本质是用既往时刻的输入和输出以及当前时刻的输入来表征当前时刻输出.NARMAX模型中的输入参数称为回归算子，如何选择并确定合适的回归算子是决定NARMAX拟合效果的关键.

另一个问题是如何确定未知映射F(·).通常采用的方法有神经网络、模糊理论、多项式拟合、小波基函数等.其中，多项式拟合作为一种线性表示，表征能力较差，且是频率无关的.本文使用单隐层神经网络来拟合F(·).单隐层神经网络作为一种最初始的人工神经网络，简单高效，对计算资源和时间的消耗很低.理论上，单隐层神经网络具备拟合任意形式函数的能力，这称之为神经网络的普遍性.虽然多层的神经网络具有更好的捕获数据特征的能力，但对于非线性拟合问题，浅层的神经网络表征能力已经足够，故无需添加层数.

一个二输入、单输出的单隐层神经网络的结构示意图如图2所示.

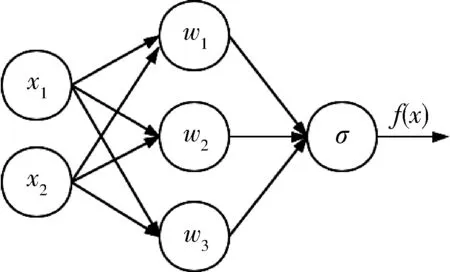
图2 单隐层神经网络Fig.2 Single hidden layer neural network

分别用x(t),H(t)和y(t)表示输入、隐层和输出层，设隐层和输出层的激活函数分别为φ(·)和λ(·)，则有：

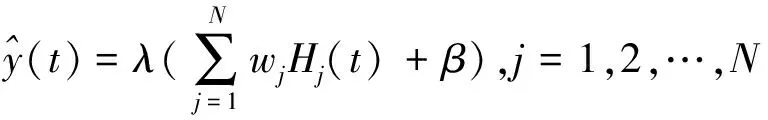
(2)

其中N为隐层节点的数目.ω、b、β为网络神经元参数，网络按照一定的学习率，通过最小化输出节点的均方误差项来更新参数.单隐层神经网络通常使用sigmoid函数作为隐层激活函数、线性函数或softmax函数作为输出层激活函数，利用梯度下降法和误差反向传播法进行训练.神经网络模型是一种简便快捷的NARMAX模型实现方法.

单隐层神经网络的另外一个优点是它的拓扑结构简单，参数更新过程不需要经历深层的反向传播，因而不容易出现过拟合现象.网络的收敛速度也非常快[14].

2 网络设计与优化

本实验采用的PEA为Physik Instrumente公司的P-885.90 (5×5×36 mm) 压电微定位器，封装在一个微小流量推进器中当做压电阀门使用.压电阀的入口和出口各安装有温度传感器，此外还有压力、流量传感器等.通过上位机安装的LabView软件控制压电阀行程并采集数据.数据预处理、神经网络搭建和优化分别使用Python3.7和MATLAB的机器学习工具箱完成.

网络的训练、验证和早期测试数据来自一组激励电压中值50 V，幅值50 V，频率0.1 Hz，共5个周期的迟滞环实验，以及一组激励电压频率从0.1 Hz逐渐上升到1 Hz的扫频实验.训练-验证-测试集的分割比例为0.7∶0.15∶0.15.其它测试数据来自多组中值、幅值、频率不同的迟滞曲线，以便充分验证其泛化能力.以上的每项输入、输出数据都被归一化到[0, 100] Hz范围内.理想情况下，在补偿掉迟滞、蠕变和温漂的影响后，网络的预测误差应当是随机噪声形式的，其来源是传感器测量噪声和环境中的机械振荡因素等.

网络设计方面，采用跨层级联的单隐层神经网络可以使输出以线性方式学习输入项特征.带级联的单隐层神经网络结构如图3所示.

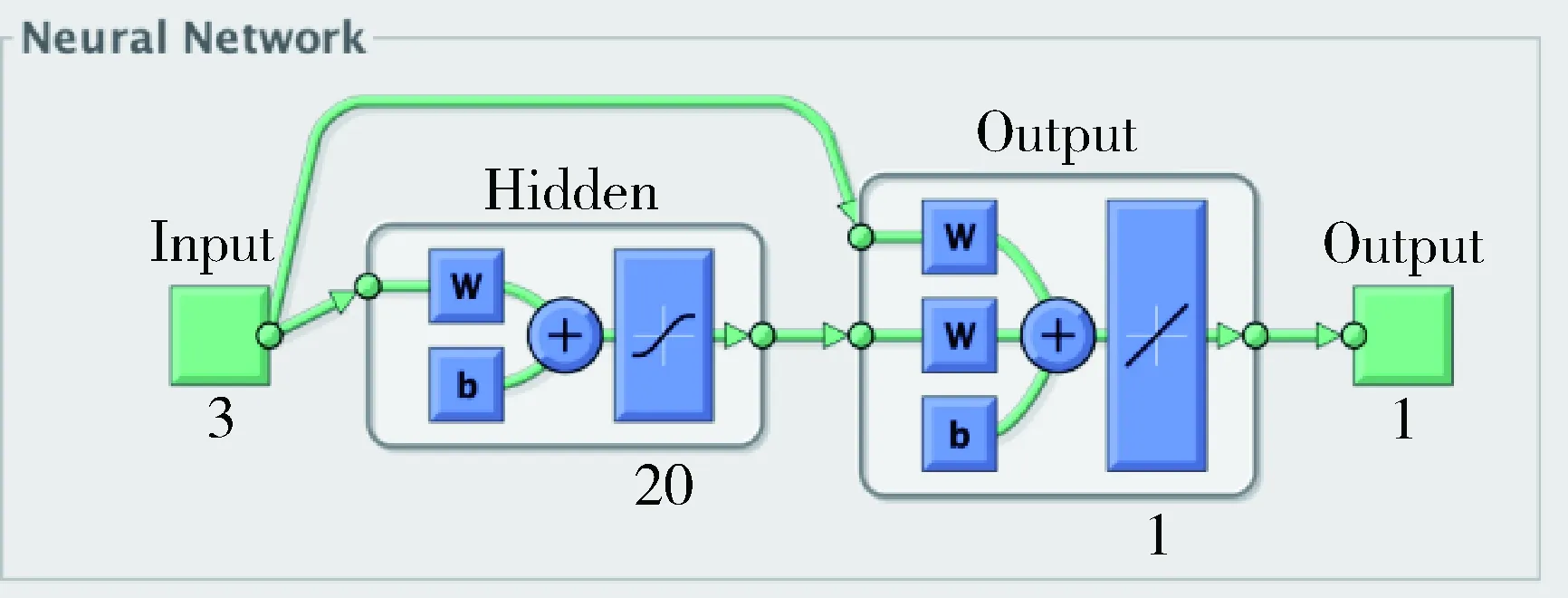
图3 级联形式的单隐层神经网络Fig.3 Cascaded single hidden layer neural network

借助信息标准确定回归算子

首先确定NARMAX模型中回归算子的选择.这一步使用一个简单的多项式模型来进行.信息标准 (information criteria)是一种基于最大似然函数的确定回归算子的方法.本文使用的信息标准衡量为AIC，以IA表示.其表达式为

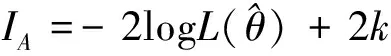
(3)

其中，L(θ)是训练数据的最大似然目标函数，k为回归算子的数量.信息标准的值会随着回归算子数量增加而迅速收敛，如图4所示．

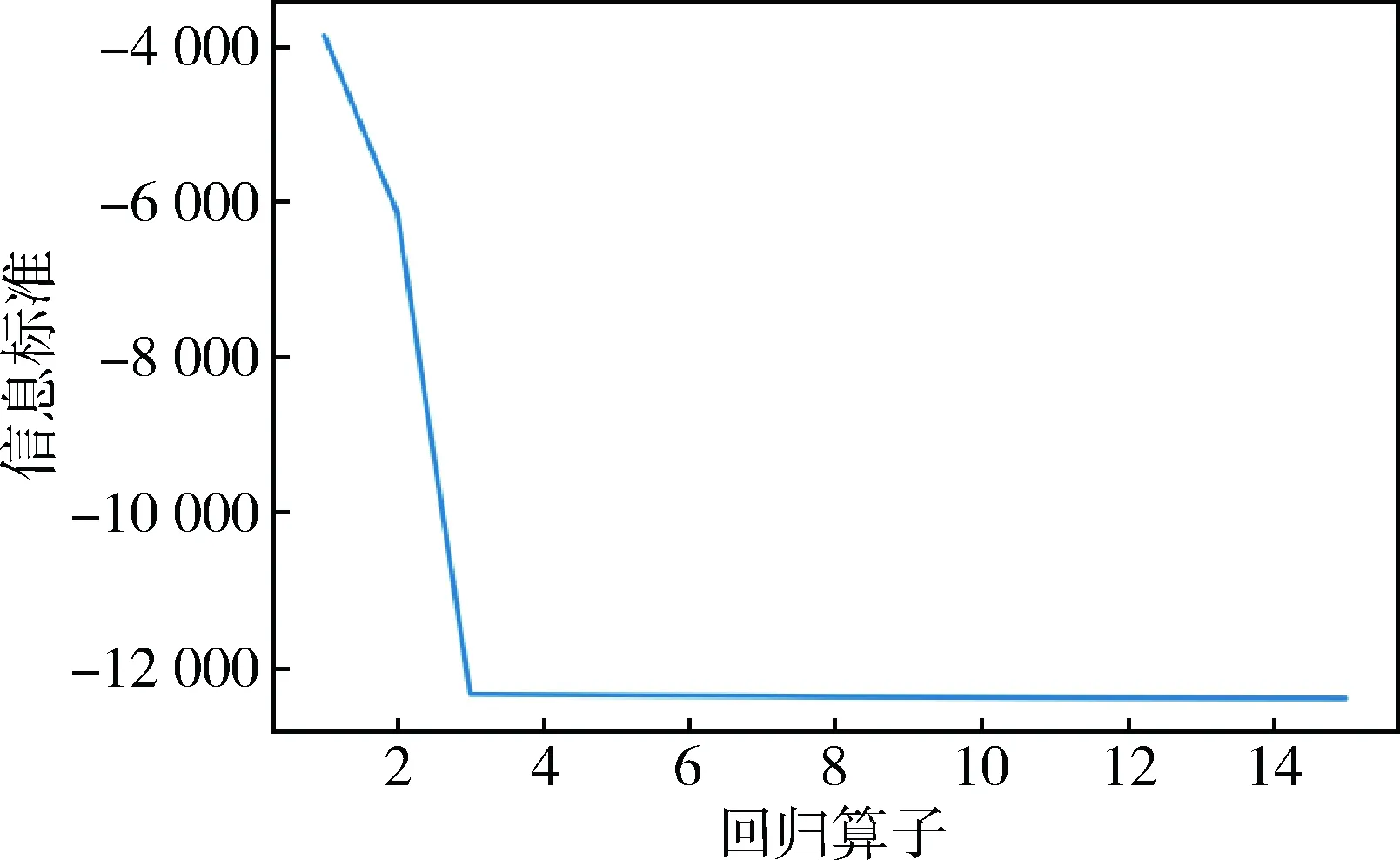
图4 回归算子和信息标准的关系曲线Fig.4 The relationship between regression factors and information criteria

利用WILSON等[15]设计的误差缩减比(ERR)算法可以进一步确定各项回归算子的比例.如表1所示．

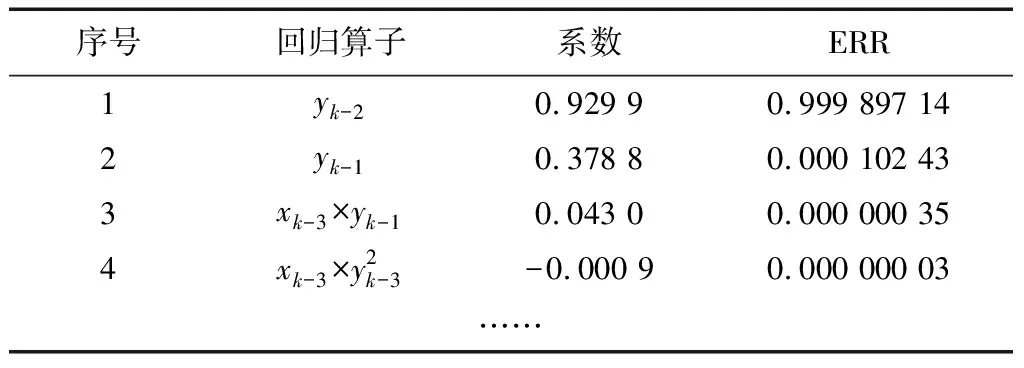
表1 回归算子对拟合误差的补偿比例Tab.1 Compensation proportions of regression operator to fitting errors

从第四项开始，回归算子对网络误差的影响下降到10-8，对拟合效果的改进非常有限.故选取yk-2,yk-1,xi-3×yi-1作为回归算子.网络的超参数选择如下：

•隐层节点数：N=10，12，14，16，18，20；

•优化方法：trainbr (贝叶斯正则化反向回归)；

•多网络融合数：5；

•最大迭代轮次：500；

•性能函数：mean squared error (均方误差)；

•训练目标：1×10-20；

•正则化参数：0.5

设置不同隐层节点数，分别进行网络训练.加入正则化参数后，网络在性能函数不再下降时停止训练，而不会依赖于迭代轮次.这可以大大减小计算资源的消耗.某次训练过程中的迭代轮次-均方误差关系如图5所示.

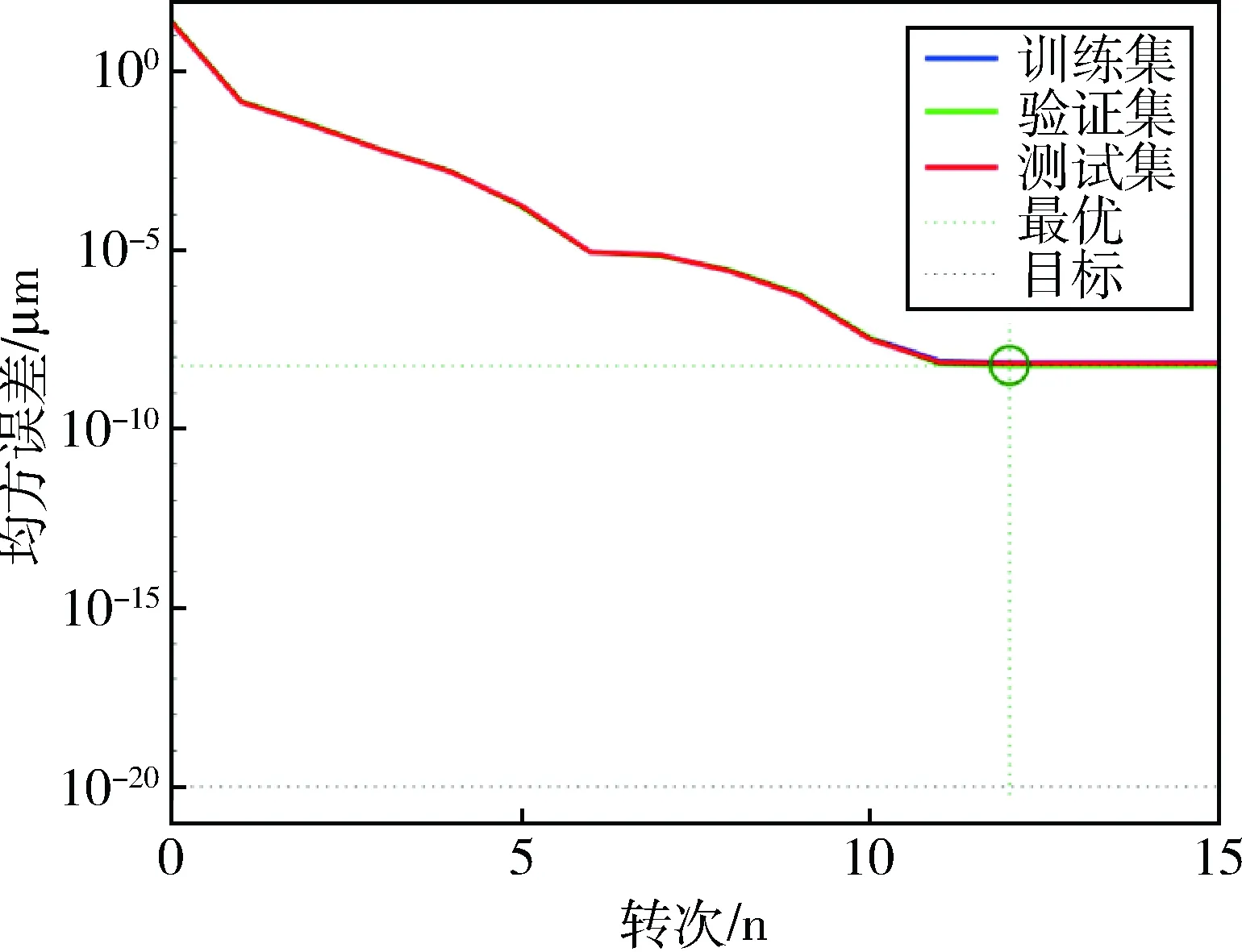
图5 训练过程均方误差曲线Fig.5 Mean square error curre of training process

以N=20为例，网络在测试集上的误差曲线如图6所示.可见此时的误差可以分为三部分，其一是随机噪声导致的误差；其二是蠕变导致的周期性误差；其三是温度变化导致的漂移误差.

将时间项、温度项、频率项进行线性处理后，作为3个独立输入节点加入网络，改进后的网络有3+3=6个输入节点.重新进行多网络融合训练.此时N=20时的测试集误差曲线如图7所示，很接近于随机噪声，说明蠕变和温漂误差得到了良好的补偿.

根据隐层节点数目的不同，网络在验证和测试集上的误差以及训练耗时如表2所示.可见随着节点数目的增加，网络的验证集MSE基本不变，测试集MSE略微下降，但同时其推理速度也会减慢，总体而言优化效果不明显.因而本文最终确定N=18作为隐藏层结构.需要注意的是，模型的最大绝对误差往往由一些异常的尖峰值导致，故测试集上的BAE会小于在验证集上的BAE，这并不是过拟合导致的.

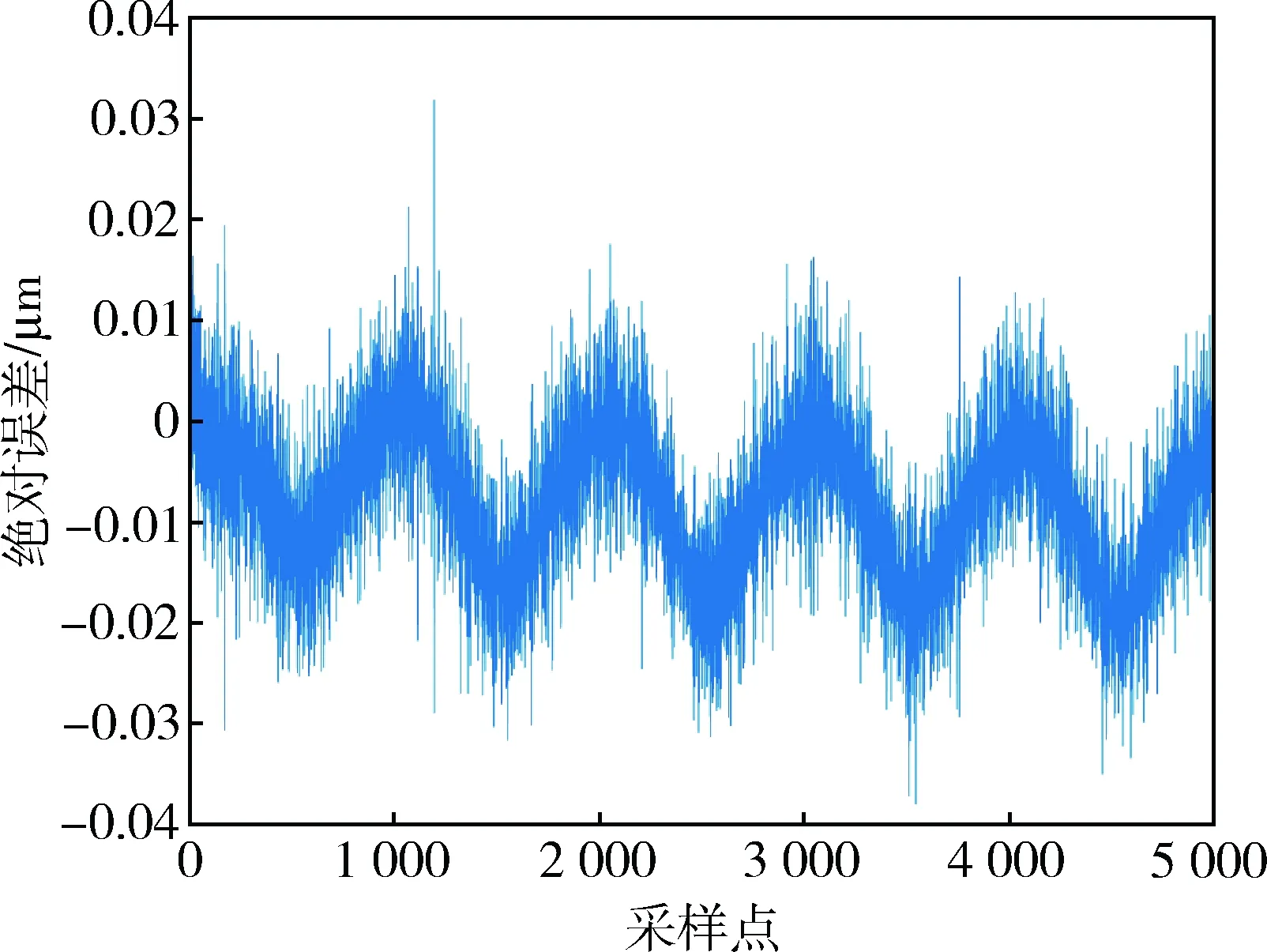
图6 N=20时测试集误差曲线Fig.6 The error curves of test dataset when N=20

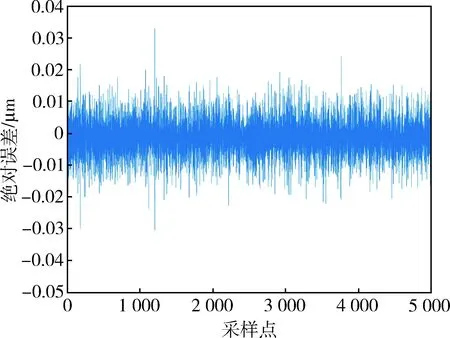
图7 改进后的网络N=20时测试集误差曲线Fig.7 The error curves of test dataset when N=20-refined network

在0.1 Hz, 0.5 Hz 和1 Hz三个不同激励电压频率的测试集上进行实验，网络的BAE和MSE列于表3中.可见，网络具有良好的泛化能力，在全频带范围内都能够很好地拟合多非线性特征.

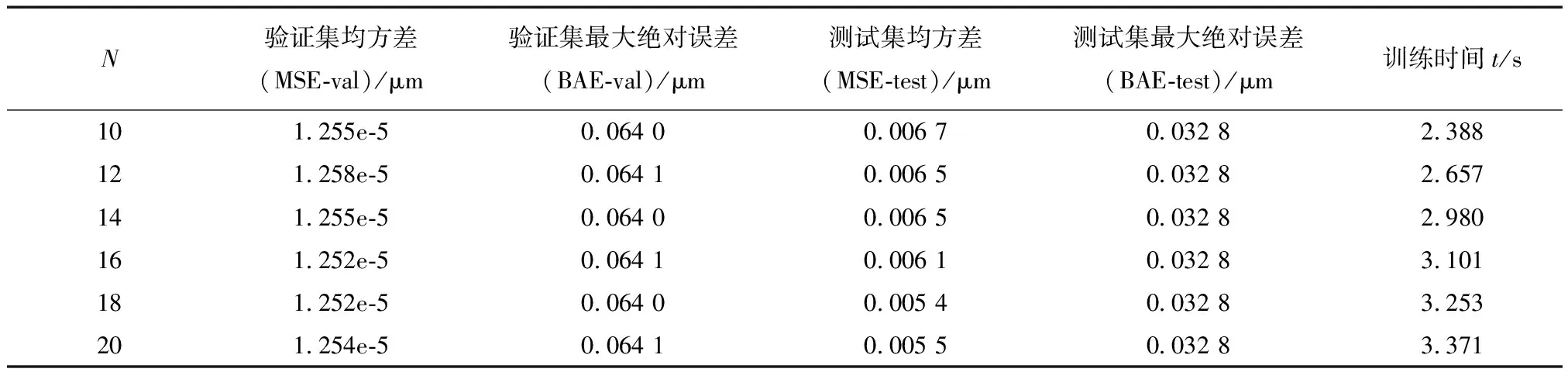
表2 针对不同隐层节点数的误差对比Tab.2 Error comparisons for different number of hidden layer neurons

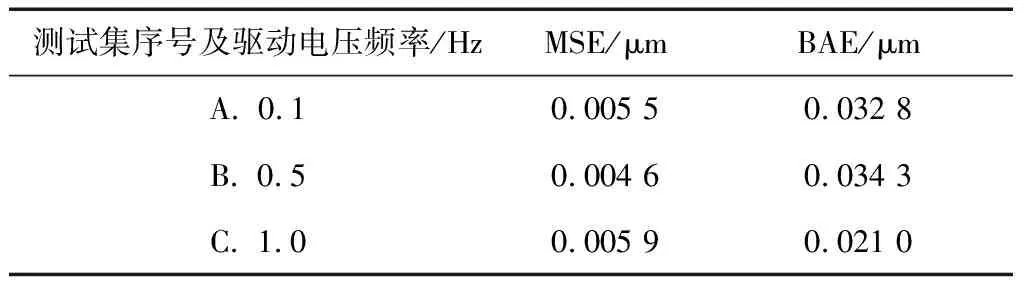
表3 不同频率下的测试集误差对比Tab.3 Comparisons of test set errors under different frequencies

3 总结与展望

本文设计了一个级联形式的单隐层神经网络来拟合周期性电压驱动下的PEA位移响应.主要结论如下：

(1)通过信息标准和误差缩减比算法，可以观察出对模型拟合效果影响最大的回归算子，进而确定神经网络的输入节点；

(2)网络在测试集上的拟合结果除环境振动和传感器测量引入的白噪声外，还呈现周期性漂移的趋势，这是温漂和蠕变非线性的影响.通过将时间、温度两项参数加入输入节点，可以补偿漂移误差；

(3)通过将扫频数据作为训练数据，把激励电压频率作为输入节点中的一项进行训练，网络可以补偿由于迟滞的频率依赖特性引入的非线性误差;

(4)级联形式的单隐层网络有利于输出同时学习输入数据的线性组合和非线性组合特征，对于线性和多非线性耦合的数据建模有一定优势.