微小卫星液化推进剂气化过程可视化检测方法

李效霖， 孙江涛*， 田文斌， 龙 军， 刘旭辉, 徐立军

1. 北京航空航天大学, 北京 100191 2. 北京控制工程研究所, 北京 100094

0 引 言

微小卫星作为大型航天器的补充，是我国未来航天领域发展的重要方向之一[1].液化气推进装置具有结构简单、体积小、安全性高、成本低等优点，因而被广泛应用于微小卫星.虽然液化气推进具有诸多优势，但亟需对系统推力器前端管路中的两相流体进行可视化并对气态推进剂含量(即气相含率)进行测量.为管路中气化机理研究和推进系统控制提供参考.

液化气推进装置所采用管道的水力直径通常设置为1～6 mm之间，针对这一区间下的气-液两相流研究相对较少，成熟的在线检测方法、模型及理论研究相对有限.现有的两相流检测方法，如模型预测法、高速摄像法、光学法和常规电学法，在微小卫星液化气推进装置的应用中均存在不足.模型预测法[2]是基于理想化假设提出的，所建模型受实验环境的限制，普适性较差，而微小卫星液化气推进装置工作在失重环境下，其内部推进剂气-液两相流流动特性则与常规管道相差较大.高速摄像法[3-4]能够获得单个或多个平面上的信息，经过数据处理可对整体参数分布进行估计，能够适用于多种流型，但却要求透明管道，同时小管道对图像的畸变作用较大[5]，在微小卫星液化气推进装置中安装高速摄像机也不易实现.对于光学法和常规电学法，光纤探针法[6]和电导探针法[7]需要将探针安装至管道内部，对管道内流体的流动存在影响.激光透射法[8]、电容测量法[9-11]只能获得单点信息、难以覆盖全部流型，因而也不适用于微小卫星的液化气推进装置.

电容层析成像(ECT)是一种适用于多相流监测的可视化技术手段.通过测量边界电容值来重建敏感场内的介电常数分布，进而获得相应物质的分布.与其他检测技术相比，ECT具有无辐射、非侵入、响应快、安装方便和成本低等优点[12-13].目前，ECT已被应用于微小管道中的多相流测量[14]，对微小卫星推进剂气化过程的机理研究具有参考意义，便于对其相含率的优化控制.因而，将ECT技术应用于微小卫星液化气推进装置具有重要的潜在价值.

传统ECT系统传感器通常由8电极、12电极或16电极构成.但在微小管道条件下，电极数较多易导致采集数据信噪比低，且加工和安装过程比较困难.因此，本文采用6电极ECT传感器来有效克服上述不足，同时选取LBP与Tikhonov正则化相结合的方法进行图像重建.针对重建图像分辨率低的问题，结合推进剂气化过程的特点，提出了基于像素插值的图像重建算法，并构建重建图像灰度值-相含率模型来测量相含率.此外，对像素插值法和灰度值-相含率模型进行数值仿真验证，并设计模拟实验装置实现初步的实验验证.

2 电容层析成像计算问题

ECT系统一般将电极以环形方式安装在管道周围，再将电压信号施加到其中一个电极，其余电极接地以获得该电极与其他电极之间的电容，之后再逐一在其他电极上施加电压信号，测量出所有独立电极对之间的电容.对于一个6电极ECT系统来说，独立测量数为

ECT中主要包括正问题和逆问题，正问题根据确定敏感区域内的介电常数的分布来确定边界各独立电极对之间的电容；而逆问题则是通过边界电容测量值来确定敏感区域内的介电常数分布.

1.1 ECT正问题

根据泊松方程，两个电极之间的互电容由给定的介电常数分布导出

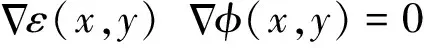
(1)

式中,ε(x,y)是介电常数分布，φ(x,y)是电势分布.两个电极之间的互电容定义为

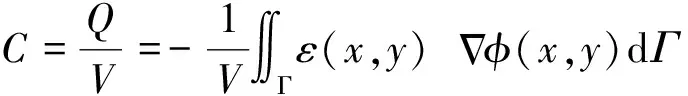
(2)

式中,V是形成电容的两个电极间的电位差，Γ是电极表面，Q是电极表面的电荷.

有限元分析(FEM)常被应用于正问题的求解.应用有限元分析可以将正问题线性归一化为

λ=Sg

(3)

式中,λ是归一化的电容向量，S是相对于归一化介电常数的归一化灵敏场矩阵.g是归一化的介电常数向量，即重建图像的像素灰度值.本文采用并联归一化

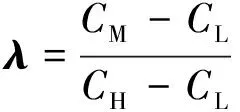
(4)

式中,CM是测量电容，CH和CL分别是高标定电容和低标定电容.

1.2 ECT图像重建算法

ECT的图像重建即是对ECT的逆问题进行求解，通过边界电容测量值来确定敏感区域内的介电常数分布.其主要面临两个问题：不定性和病态性.为了解决这两个问题，国内外提出了许多图像重建算法.

将式(4)中S视为从介电常数向量空间到电容向量空间的线性映射，那么就可以将ST近似看作从电容向量空间到介电常数向量空间的线性映射，进而可以给出近似解

(5)

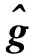
Tikhonov正则化算法[16]常被用于求解逆问题，标准Tikhonov正则化等效于求解以下方程：

(STS+μI)g=STλ

变换后即可得到

g=(STS+μI)-1STλ

(6)

这种方法被称为Tikhonov正则化算法.Tikhonov正则化能够较好的重建图像，通常可以得到较LBP更好的结果.但正则化参数μ的选择对成像质量的影响较大，且几乎只能凭经验选择.μ较小时，Tikhonov正则化成像结果受噪声影响较大，但直接增大μ会使图像过于平滑，准确度差.本文中，选取μ=0.001.仿真和实验结果表明，在Tikhonov正则化图像上叠加LBP，能够在间接增大μ的同时又不过度平滑重建图像.本文采用Tikhonov正则化和 LBP重建结果的加权平均作为最终的重建图像

g′=μLgL+μTgT

(7)

式中,g′是最终的重建图像，gL和gT分别为LBP和Tikhonov正则化的重建图像，μL和μT分别为两种重建图像的加权系数，如此可在保证成像质量的同时，一定程度上减少噪声的影响.本文中，选取μL=μT=0.5.此外，针对小管道内气液两相流的特点，本文提出了一种基于插值的图像重建算法，具体将在1.3中介绍.

广泛应用的ECT重建算法还有Landweber迭代算法

gk+1=P[gk-αST(Sgk-λ)]

(8)

其中,α是固定的松弛因子，P是投影算子.

此外，TAYLOR等[17]提出了灵敏因子正则化(SFR)方法用于ECT成像.首先将灵敏场矩阵S、测量电容向量λ和介电常数向量g进行扩展，将式(4)改写为

其中，DS是非零元素为S列和的对角阵，x为灵敏因子向量.之后采用Tikhonov正则化进行求解

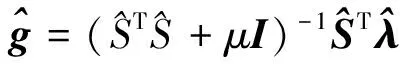
(9)

该方法引入了新的约束，一定程度上降低了问题的不定性.同时，此方法与本文提出的像素插值法均对式(4)中的向量和矩阵进行了扩展，增加了先验知识，故引入作为对比验证.

本文使用图像相对误差γ来评价实际介电常数分布与重建图像之间的偏离程度[18]

(10)

其中g0是测试对象的实际介电常数分布，g是重建图像的介电常数分布.

1.3 像素插值法

6电极ECT系统成像仅有15个方程，不定性强，求解困难.本文中ECT测量的是推进剂在管道中的气化问题，常存在较多细小液滴[1]，呈雾状流.ECT成像分辨率较低，难以给出液滴的精细分布图像，而每个像素点区域的等效介电常数会受液滴分布浓度的影响.推进剂在管道中气化时，液滴浓度不会突变，会由高浓度逐渐变化为全气相.因此，可将敏感区域内等效介电常数的空间变化近似为线性变化，应用双线性插值的方法得到新的约束方程，增加了逆问题求解方程的数量，有助于提高图像重建质量.具体算法流程如下

单位面积内，若已知I[0,0],I[0,1],I[1,0],I[1,1]，则双线性插值公式为：

I[rx,ry]≈I[0,0](1-rx)(1-ry)+

I[0,1](1-rx)ry+I[1,0]rx(1-ry)+I[1,1]rxry

(11)

假设式(11)成立,则可以重写为

-I[rx,ry]+I[0,0](1-rx)(1-ry)+

I[0,1](1-rx)ry+I[1,0]rx(1-ry)+

I[1,1]rxry=0

设定归一化重建图像的元素按照从左到右、由上至下排列的顺序组成向量g，并从图像中周期性的选择边界点，将图像划分为P×Q个区域，有

式中X、Y分别是图像中横向和纵向的像素数量，Δx、Δy分别是横向和纵向的周期.

对于图像内一点I[x,y]来说，其在向量g中对应的元素为

g[x+yX]

在划分的区域内，位于I[x,y]左上角的元素是

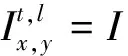
式中,mod为取余符号，其在向量g中对应的元素为

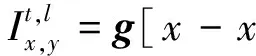
类似的，其他3个角在向量g中的对应元素为

划分出的区域可以归一化表示为

然后，再根据向量g和式(11)建立XY-(1-P)(1-Q)个新方程

或者写作：

g[x-xmod Δx+(y-ymod Δy)X](1-rx)(1-ry)+

g[x+x-xmod Δx+(y-ymod Δy)X](1-rx)ry+

g[x-xmod Δx+(y+y-ymod Δy)X]rx(1-ry)+

g[x+x-xmod Δx+(y+Δy-ymod Δy)X]rxry-

g[x+yX]=0

这些插值方程写成矩阵形式为

Hg=O

(12)

式中O是有XY-(1-P)(1-Q)个元素的零向量.将式(12)与式(4)合并，写作

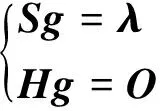
或者写作

Ag=b

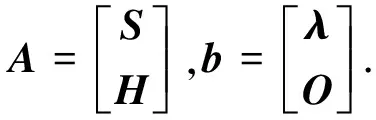
将A、b代入式(5)和式(6)代替S和λ，再通过式(7)进行加权平均即可获得像素插值法的重建结果.

2 仿 真

2.1 传感器建模

传感器模型采用有限元分析软件COMSOL Multiphysics 搭建，如图1所示.其中微小管道采用外径6 mm,内径4 mm的PVC管，在外管壁均匀布置6电极阵列，并在最外围安装一个直径为8 mm的屏蔽层.这与本文实验所用ECT传感器结构一致.

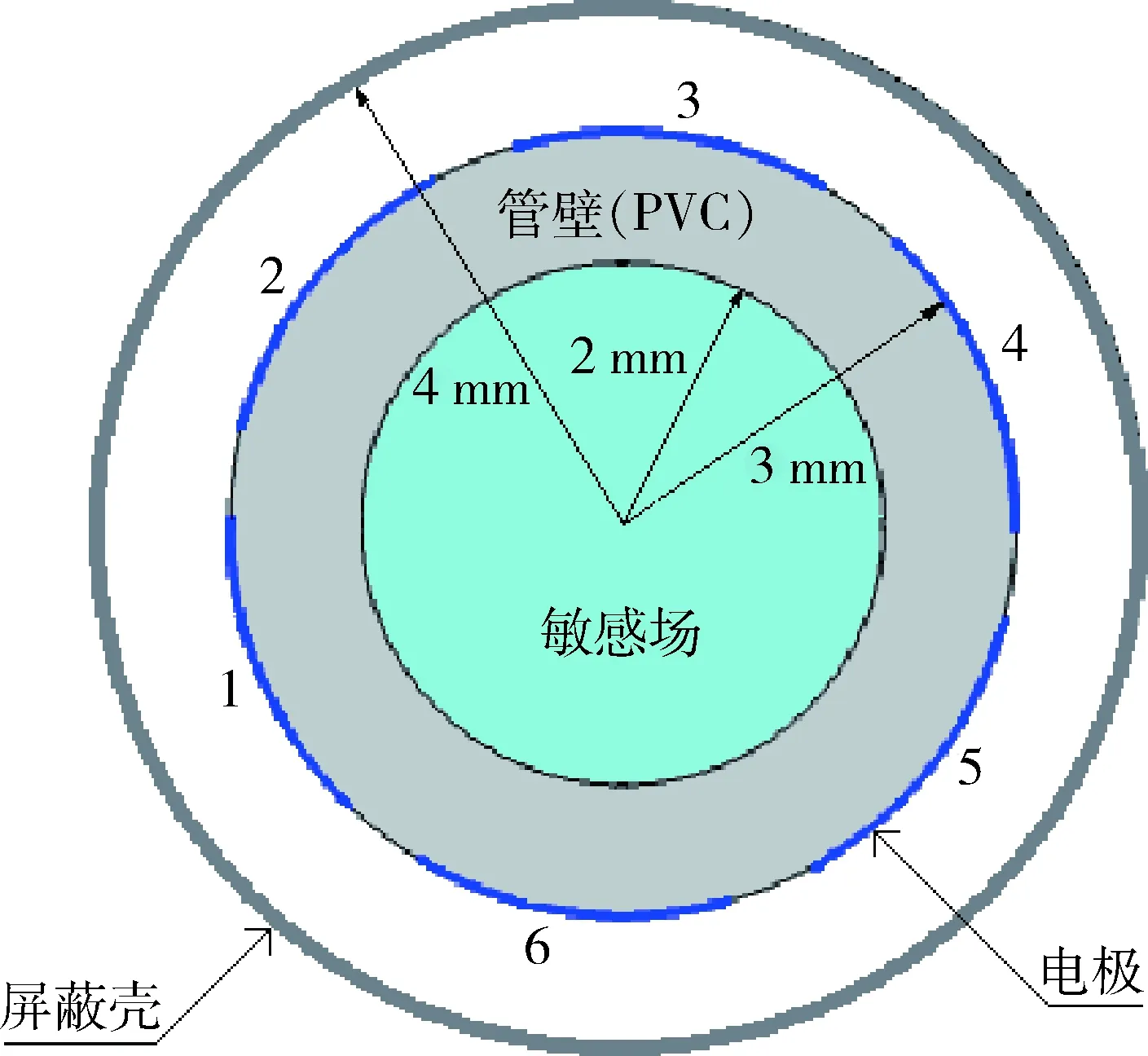
图1 6电极ECT传感器模型Fig.1 6-electrode ECT sensor model

灵敏场矩阵中的元素定义为i,j电极对之间电容对敏感场内某点介电常数变化的灵敏度，计算如下：

式中,Vi，Vj分别为电极i,j上施加的激励电压，φi(x,y)，φj(x,y)分别为施加激励电压Vi，Vj后点(x,y)的电势分布，部分电极间灵敏分布如图2所示.

图2 6电极ECT系统的灵敏场Fig.2 Sensitive field of 6-electrode ECT system

2.2 图像重建仿真实验

利用COMSOL Multiphysics建立层状流、环状流等典型流型的仿真模型，对像素插值法进行测试验证.表1是像素插值与其它图像重建算法在仿真流型下的结果对比.其中，LBP、Tikhonov和Landweber是较为常用的成像算法.像素插值法实际上基于LBP和Tikhonov求解逆问题，故将不添加像素插值的LBP和Tikhonov融合结果式(7)引入对比，记作LBP+Tikhonov.SFR算法也将灵敏场矩阵S进行了拓展，也列出作为参考.由表1可以得出，像素插值法较其他算法相比具有一定优势.对于层状流和环状流，像素插值算法能够重建出较为清晰的气液两相分界面；对于含有两个气泡的泡状流，像素插值算法能够有效区分两气泡，且重建位置相比其它算法更为准确，同时能够明显分辨出气泡的大小.由于ECT在边缘处灵敏度较高，传统方法重建图像的气泡容易向边缘处偏移，但像素插值算法的重建图像确并没有明显的偏移，这是由于像素差值引入的新约束能够一定程度抵消灵敏场分布不均匀的负面影响.由于像素插值法可实现在线重建，是在LBP+Tikhonov基础上的改进而来的，本文将LBP+Tikhonov作为对照，对像素插值图像重建的效果进行进一步验证.更多仿真样本下的LBP+Tikhonov与像素插值重建图像的相对误差对比见图3.应用像素插值后，图像相对误差大都能下降10%以上，图像质量显著提高.

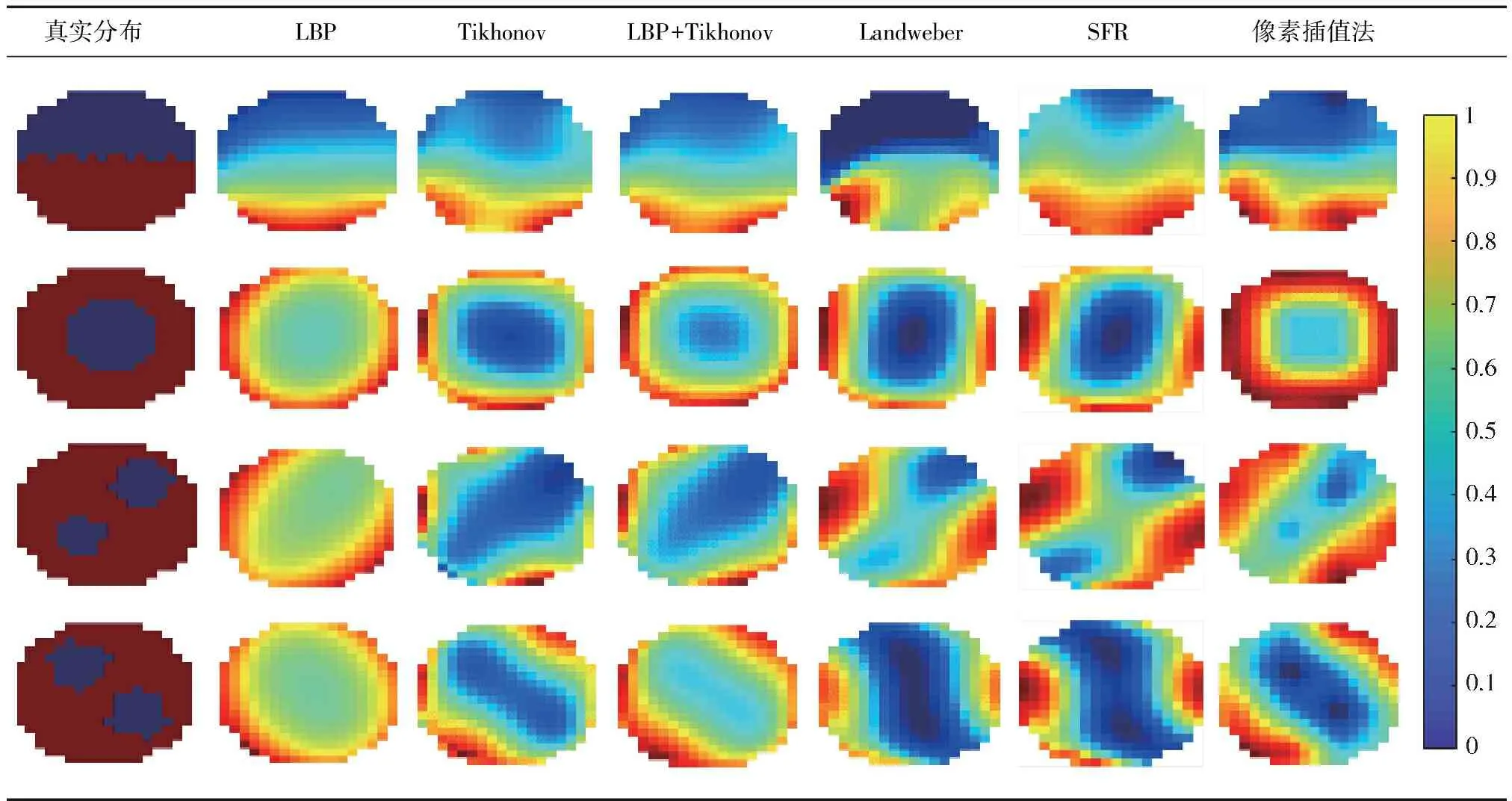
表1 像素插值法图像重建和其它图像重建算法对比Tab.1 Comparison of pixel interpolation image reconstruction and other image reconstruction algorithms

为验证像素插值法的可靠性，对20组仿真电容数据附加信噪比60 dB到40 dB的高斯白噪声来模拟实际测量中的测量噪声，再通过电容插值重建算法成像，计算其图像相对误差，测试并验证电容插值重建算法的可靠性.信噪比SNR定义为：

式中，Signal和Noise分别为仿真电容值和噪声值的均方根.在不同噪声水平下，图像相对误差均值如图4所示，随着SNR的增加，重建图像的相对误差有一定的上升，但像素插值法的相对误差较LBP+Tikhonov方法更小.当SNR大于42 dB时，像素插值法重建图像的相对误差只出现小幅上升，因而具有较好的抗噪声能力.在保证电容测量精度的情况下，像素插值法相比传统方法能够给出更好的重建结果.

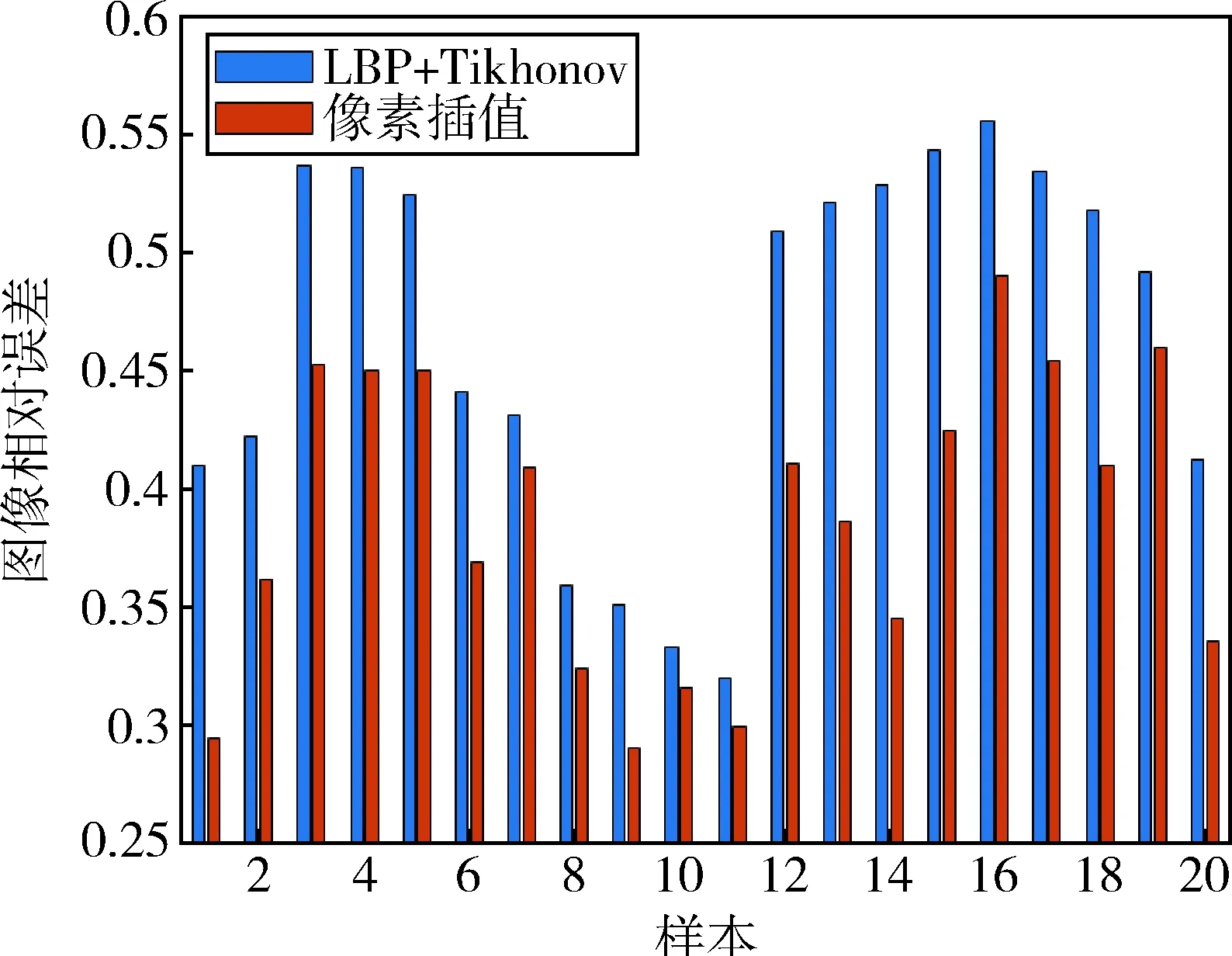
图3 图像相对误差对比Fig.3 Comparison image relative error

图4 附加噪声后的图像相对误差对比Fig.4 Comparison of relative image error after adding noises

2.3 灰度值-相含率模型

本文中的相含率为体积含气率，计算公式如下

其中Ag和Al分别指气-液两相流气相和液相的体积流量.

通过图像重建，可获得图像灰度值g.g越小则意味着该像素流体成分越接近气相.计算相含率前先对灰度值g进行归一化.将满场电容CH和空场电容CL采用像素插值法进行图像重建，图像灰度值记为gH、gL，再使用gH、gL对重建图像进行归一化处理：

式中g′是归一化后图像灰度值.对g′进行积分即可得到相含率：

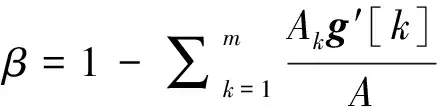
(13)

式中m为像素数量、g[k]为第k像素的灰度值、Ak为第k像素的面积，A为图像总面积.

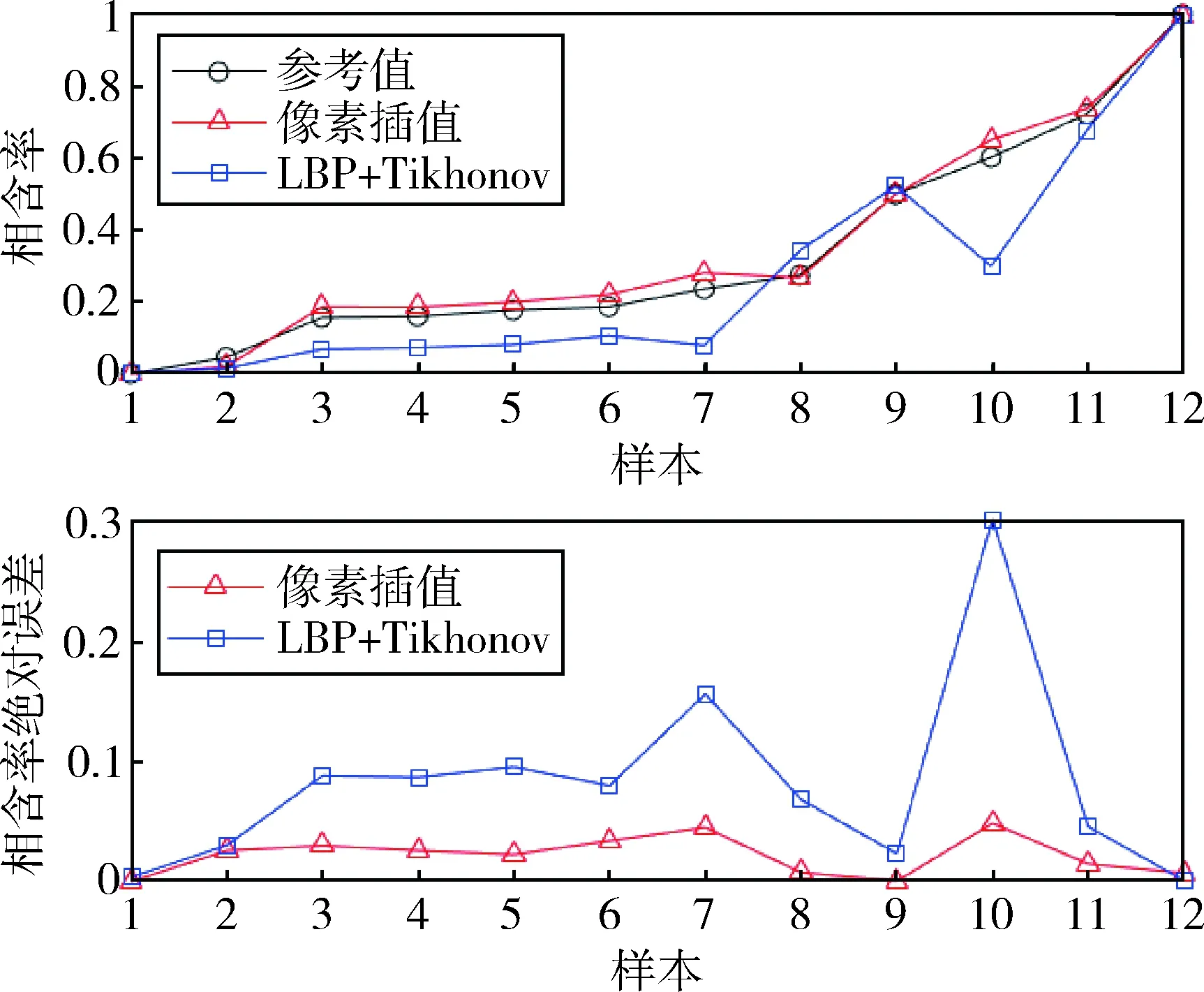
图5 相含率测量结果和绝对误差对比Fig.5 Comparison of void fraction measurement results and absolute error

灰度值-相含率模型在仿真样本下得到的测量结果和绝对误差如图5所示.样本的流型为环状流、层状流和泡状流，相含率参考值较为均匀的分布在0-1之间.在仿真条件下，像素插值法结合灰度值-相含率模型的最大绝对误差和平均绝对误差分别为4.86%和2.17%，远小于仅结合LBP+Tikhonov的测量误差.

3 实 验

本文基于微小卫星液化气推进装置的实际情况设计了模拟实验装置.在推进装置方面，贮箱采用外径50 mm，内径32 mm的亚克力罐.电动阀采用Kamoer公司KVE21PS24N2N651A型电磁阀.推进剂管道采用外径6 mm，内径4 mm的透明石英进行管模拟.在ECT传感器方面，设计的柔性PCB电极如图6所示，将其按图1方式安装在石英管道周围；数据采集系统采用北京航空航天大学过程监测与信息技术实验室设计的高速数字式多通道ECT数据采集系统[20]；PC作为成像上位机，Matlab作为成像软件.整体实验装置示意图如图7所示.实验时，模拟推进剂储存于形状与微小卫星液化气推进装置中推进剂的贮箱类似的模拟贮箱中，开启电磁阀使之迅速气化，并以气液两相的形式由石英管道末端喷出.

图6 柔性PCB制作的ECT系统电极Fig.6 ECT sensor made of flexible PCB

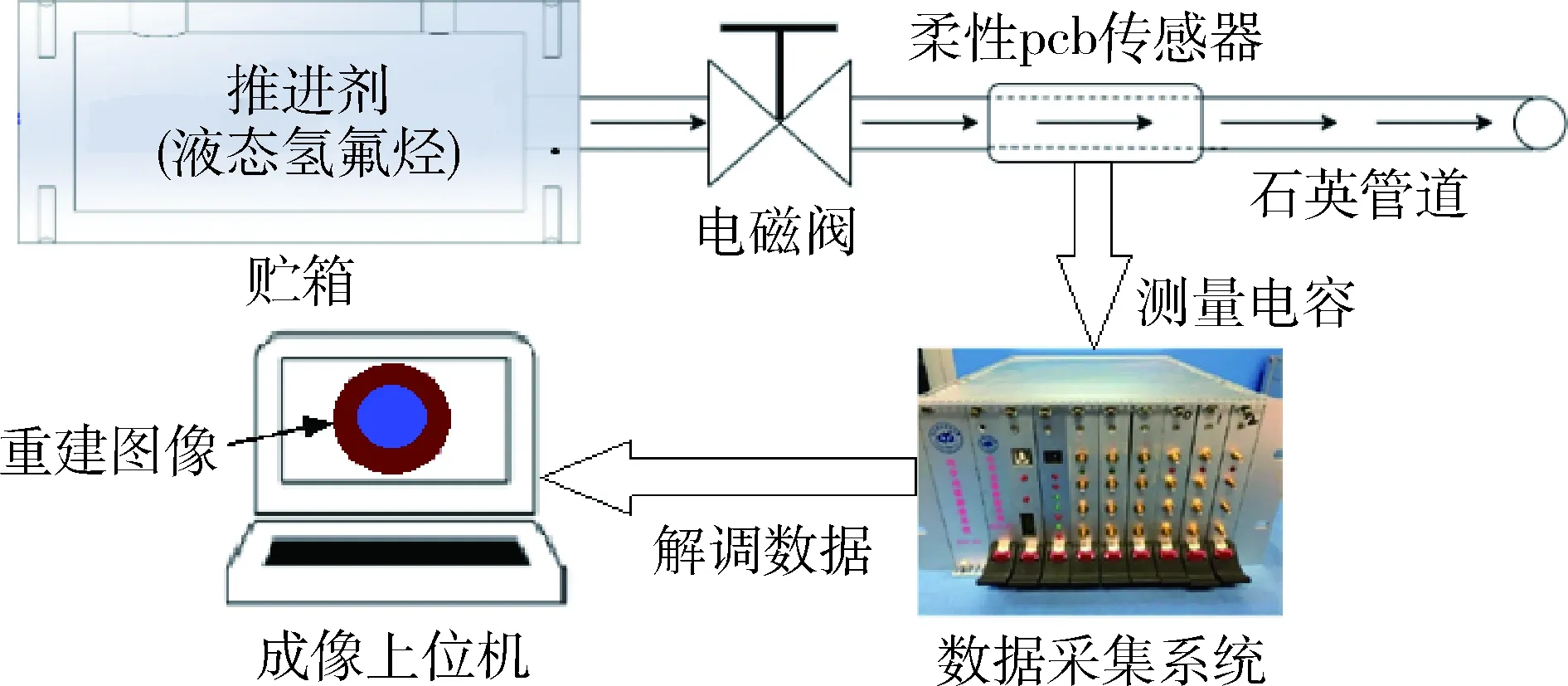
图7 实验装置示意图Fig.7 Schematic diagram of experimental setup

3.1 实验方法

上海展途化工有限公司生产的氢氟烃清洁气在实验装置内的气化过程被用于模拟实际推进剂的气化过程.氢氟烃常应用于制冷、灭火、清洗等行业，航天领域内，可用作发射火箭的湿剂[21].同时，氢氟烃清洁气常温下无色无味、不可燃且不导电，液态下介电常数与实际液推进剂也较为类似.因此，氢氟烃清洁气适合在实验条件下对液化气推进装置中的推进剂进行模拟.

图8 喷出贮箱的氢氟烃Fig.8 HFC ejected from the storage tank

液态氢氟烃储存于实验装置贮箱内时，贮箱内压力为0.6 Mpa.实验开始时，电磁阀开启，贮箱与电磁阀接口处氢氟烃压力下降并迅速气化，经由石英管道向外界喷出.4 mm内径下，氢氟烃在石英管内的气化也并不完全，呈气液两相混合状态.因此，该气化过程适合对微小卫星液化气推进装置管道中推进剂的未完全气化过程进行模拟.

图像重建需要归一化电容λ，除测量电容Cm外，获取归一化电容λ还需要测得高低标定电容CH和CL.将管内填充满空气，测量各电极间电容即可得到CL.测量CH时应使管道内填充满液态的氢氟烃清洁剂，但这几乎无法做到，所以CH是难以测量的.文献[22]中提出了一种估算CH的方法.将管内填满另一种已知介电常数的物质，此处为食盐(氯化钠)，然后再测量各级间电容可得到Cm，进而可以算得管壁电容CW和静电容CO：

式中,εrL为空气的相对介电常数，εrm为所使用已知介电常数物质的相对介电常数.求得CW和CO后，将液化气可能的最大相对介电常数设置为εrH，即可算得高标定电容CH：

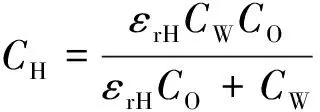
(14)

图9中分别为测得的CL、Cm、和估算出的CH.其中空气的介电常数εrL=1，食盐的介电常数εrm=3，氢氟烃液体可能的最大相对介电常数εrH=1.9.

图9 模拟实验装置中测得的CL、Cm、和估算出的CHFig.9 Measured CL,Cm in the experiment and estimated CH

3.2 实验结果

打开电磁阀使贮箱中的液态氢氟烃喷入石英管道，氢氟烃在透明石英管道内的流动状态如图10所示，可明显看出管道内有液体存在.参考与氢氟烃气化过程较为类似的天然气管道内天然气气化过程[23]和制冷剂R134a在石英玻璃直喷管中的流动状态[19]判断图10中左侧管道内两相流体应处于环状流到雾状流之间的状态，安装在右侧的传感器内部管道内应为环状流.通过对管道内氢氟烃的分布进行图像重建并计算出其相含率.

图10 透明石英管道内的氢氟烃空气流动Fig.10 HFC flow in transparent quartz pipe

首先，为测试装置的可靠性，利用下式计算实验装置的信噪比，

实验环境下，氢氟烃在石英管道中的流型比较单一，因此，测试了两组共110个测量数据.将第一组测量数据均值视为测量电容CM与高标定电容CH和低标定电容CL对比如图11.使用像素插值法对其进行图像重建的结果如图12左所示.由重建图像可知，石英管道内的氢氟烃大致为环状流，管壁处接近液态，管道中央接近气态，与分析结论相同.使用灰度值-相含率模型计算出其相含率为0.263 3.测量第二组测量数据时，贮箱内液态氢氟烃经过了一段时间的消耗，质量变小，压力也变小，进而其喷出管道的流速也将变慢，气化更充分，基于这些原因，第二组测量数据计算出的相含率应当比第一组测量数据要大.其重建图像如图12右所示.测得其相含率为0.418 6，大于第一组测量结果，与推测结论相符.

图11 第一组中的CM、CH和CLFig.11 CM,CH, and CL in the first dataset

图12 两组测量数据的重建图像Fig.12 Reconstructed images from the two sets of measurement data

综上所述，结合提出的像素插值，利用ECT成像系统在实验环境下能够对气-液两相流的流动状态进行图像重建，利用灰度值-相含率模型能够实现对相含率的测量.

4 结 论

针对微小卫星液化气推进剂气化不完全的问题，本文设计了6电极电容层析成像系统和液化推进剂模拟实验装置；提出了像素插值法与灰度值相含率模型.经过仿真和实验分析，结果表明：像素插值法重建图像质量优于其他方法获得的6电极ECT系统重建图像，图像相对误差大多能够下降0.1以上；像素插值法结合灰度值-相含率模型对相含率进行测量的精度远高于常规图像重建算法，仿真验证最大误差约4.86%；搭建的实验装置能够对微小卫星液化气推进装置的工作状况进行模拟；6电极电容层析成像系统结合像素插值法和灰度值-相含率模型能够对气-液两相流的相含率进行有效测量.