基于强度折减法的巴彦哈尔露天边坡稳定性分析

张冬岩，苗勇刚，张长锁

（1 内蒙古金中矿业有限公司，内蒙古 锡林郭勒 011300；2 矿冶科技集团有限公司，北京 100160）

传统的极限平衡理论分析边坡稳定性时没有考虑应力应变关系，不能通过计算收敛求解安全系数，在求安全系数时需要先假定滑移面失稳模式，并且通过简化切片方法求解安全系数，导致精度降低，与真实的安全系数偏差较大。而有限元能够模拟岩土体受各种边界条件下应力应变关系，有限元强度折减法经常用于模拟边坡稳定性，并得到了许多学者的认可。Zienkiewicz 等人早在1975 年就将强度折减法应用于边坡稳定性分析[1]。之后由Donald 和Giam[2]，Matsui 和San[3]等人在实践中应用并不断改进。郑颖人[4]、唐芬[5]等人根据强度折减原理、屈服准则等方面开展了进一步的研究，提高了计算精度，扩大了在实际工程中的应用范围[6]。

1 强度折减法分析边坡稳定性的优点

强度折减法已被许多成熟的岩土工程有限元软件所应用，主要的优点如下[7]：

（1）通过重力载荷的施加和剪切强度的降低而自动产生的剪切应变可以找到临界破坏面；

（2）求解安全系数时，不用先假定边坡破坏的形状，也无需进行条分。

（3）它适用于具有复杂地貌、地质的边坡进行计算，并且可以提供极限平衡分析法无法实现的信息，例如应力，运动和孔隙压力。

2 北露天边坡概况

巴彦哈尔金矿矿区构造处于隆起带复式背斜西端收敛部位，构造较为简单。断裂带呈北东—南西向分布，但破碎带内已被断层角砾岩贯入[8]。一般地表风化强烈，强风化带60 ～80 m 左右，其下逐渐过渡为中等风化、弱风化或完整基岩，边坡不易发生整体性滑坡，但是可能发育小型的崩塌地质灾害。根据巴彦哈尔金矿北露天边坡的工程地质特征，选取具有典型意义的能反映巴彦哈尔金矿北露天边坡稳定性的63 线（矿体下盘）和71 线（矿体上盘）工程地质剖面作为分析剖面，选取的两条工程地质剖面图如图1～2 所示。

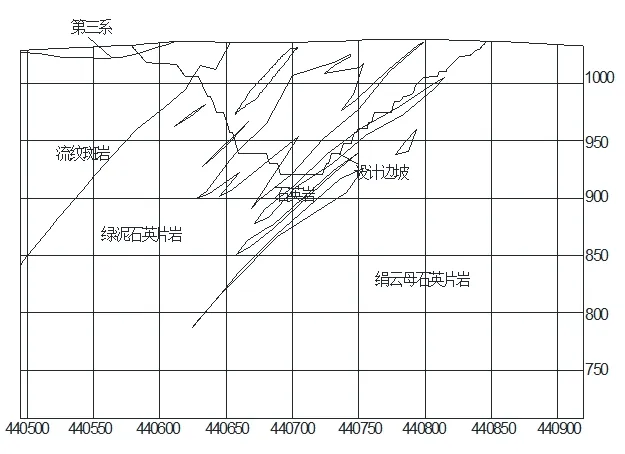
图1 63 线工程地质剖面

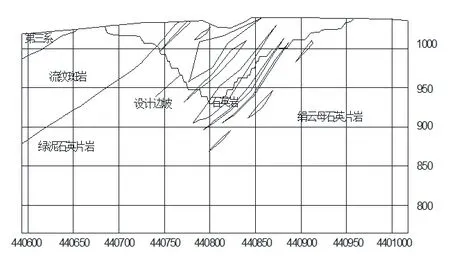
图2 71 线工程地质剖面

3 强度折减法基本原理

强度折减系数法的基本原理是将材料的粘结力和摩擦角参数值同时除以折减系数F，得到新的值，将该值作为新的参数再进行循环计算。通过不断折减，当结果不收敛时，所得到的值称为边坡最小稳定安全系数，此时边坡达到极限平衡状态，发生剪切破坏，同时可得到边坡的破坏滑动面[9]。表达式如下：

式中：C′—折减后的粘聚力，KPa；φ′—折减后的摩擦角，°；F—折减系数。

4 边坡稳定性的有限元分析

4.1 岩体力学参数

根据露天边坡开挖后岩体的分布特点，本研究考虑了5 种岩性，即绿泥石英片岩、流纹斑岩、绢云母石英片岩、石英岩、第四系，其力学性质如表1 所示。

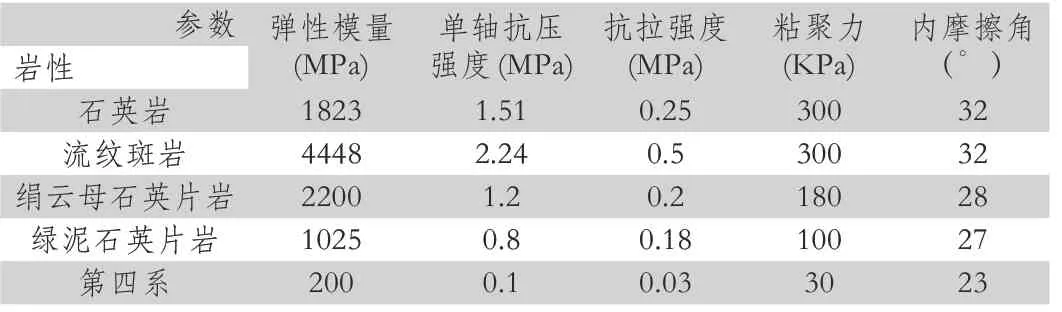
表1 露采边坡岩体力学参数

4.2 计算模型

根据选取的63 线（矿体下盘）和71 线（矿体上盘）分析剖面，分别建立M1（坑底标高900，边坡角为42°）、M2（坑底标高900，边坡角为40°）两个有限元分析模型（如图3 ～4 所示），进行平面应变分析，主要分析边坡在自重应力场作用下的稳定性情况。

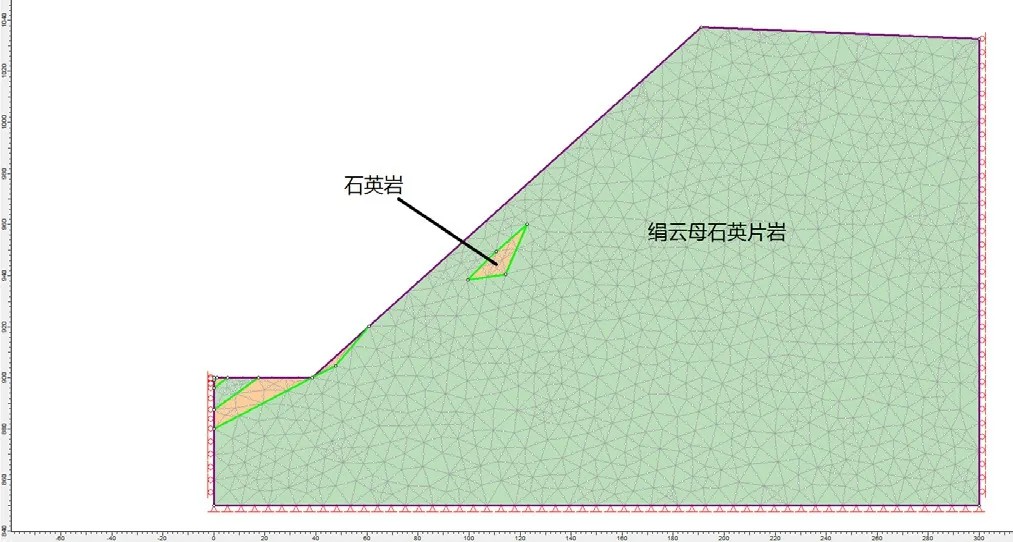
图3 M1 模型有限元网格图

边界条件为：边坡两侧水平方向固定，底部垂直方向固定，坡面为自由面，顶部为自重应力场。

根据Mohr-Coulumb 屈服准则和最大拉应力判据来确定边坡开挖后可能出现的应力、位移、拉剪破坏范围等，以此来分析巴彦哈尔金矿北露天边坡的稳定性状况。

数值模拟采用加拿大岩土工程分析软件Phase2 8.0，主要应用于地下或地表边坡工程开挖中的应力和位移分析，可用于分析模拟地下硐室开挖与支护、边坡开挖等问题。在进行分析时的载荷按程序自动分级施加，解方程时用Gaussian 消除法求解，最大重复次数为500 次，累计误差为0.001[10,11]。

图4 M2 模型有限元网格图

5 计算结果及分析

5.1 M1 模型分析结果

（1）应力分析

通过对M1 模型的最大应力等值线分布图（如图5 所示）可以看出：最大应力值随埋深的增加而增大，接近边坡坡面时最大主应力值变小且呈顺坡方向变化，在坡体的下部受开采扰动的影响，应力变化较大，坡面及坡面附近存在一定的拉应力，最大值的为0.2MPa。

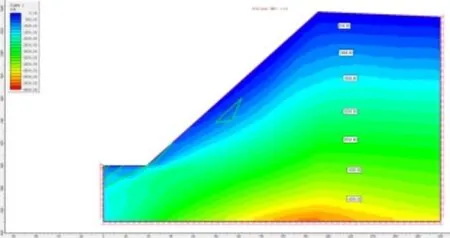
图5 M1 模型的最大主应力等值线（σ1）分布图

（2）位移分析

根据位移矢量图可以看出，M1 模型开挖后边坡受自重应力和地质构造影响坡体的位移方向主要朝向采坑临空面（如图6 所示），位移较大处为坡体中部范围，最大值为0.09m。

图6 M1 模型的位移矢量分布图

（3）破坏区分析

M1 模型边坡破坏主要表现为拉剪破坏，如图7 所示。拉应力破坏区主要分布在坡顶，向坡体内延伸的最大深度约为30m；坡体中部以上坡面处也存在少量拉应力破坏区，最大深度约为18m。剪切破坏区主要分布在坡体上部岩体和坡脚。从坡顶往坡体内约20 ～30m 处开始向坡体内发展，最大延伸深度为55m；坡脚的剪切破坏区最大深度为22m。

图7 M1 模型的最大剪应变分布及拉剪破坏区域图

（4）安全系数分析

最后利用强度折减法计算的安全系数为F=1.21，表明边坡处于极限平衡状态，在不受外界因素影响下是稳定的，符合一般规律，结果可靠。

（5）滑动机理分析

图8～9 为M1 模型强度折减法计算安全系数的过程，从强度折减系数F 取值为1.0、1.18、1.21 和1.25 时计算出的边坡最大剪应变和剪切破坏分布情况，可以看出，坡顶及坡脚发生剪切破坏，随着折减系数增大，坡顶剪切破坏区范围向岩体内扩展，坡脚破坏区逐步向上延伸，当折减系数增大到1.21 时，剪切破坏区在坡体内贯通，此时模型计算不收敛，滑面形状为近似圆弧形，边坡滑动失稳模式为圆弧滑动。当折减系数增大到1.25 时，边坡沿着滑动面发生蠕变滑动，造成边坡整体失稳。

图8 M1 模型F=1.21 时最大剪应变分布图

图9 M1 模型F=1.25 时最大剪应变分布图

5.2 M2 模型分析结果

（1）应力分析

通过对M2 模型的主应力等值线分布图，如图10 所示可以看出：最大应力值随埋深的增加而增大，接近边坡坡面时最大主应力值变小且呈顺坡方向变化，在坡体的下部受开采台阶的影响，其应力的扰动状态较大，坡面及坡面附近存在一定的拉应力，最大值的为0.4MPa。

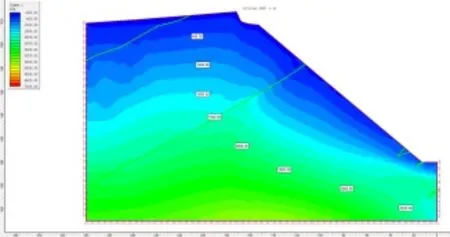
图10 M2 模型的最大主应力等值线（σ1）分布图

（2）位移分析

M2 模型开挖坡体的位移主要是向采坑临空面移动（如图11所示），位移较大处为坡体中部范围，最大值为0.12m。

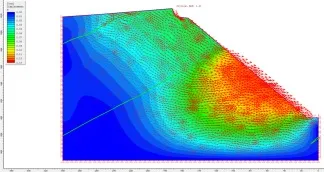
图11 M2 模型的位移矢量分布图

（3）破坏区分析

M2 模型坡体的破坏区主要为拉应力破坏区和剪切破坏区（如图12 所示）。

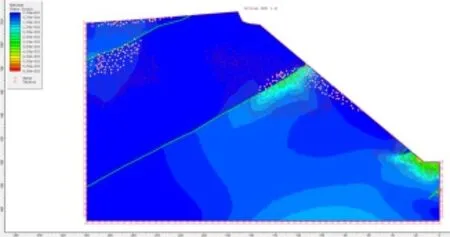
图12 M2 模型的最大剪应变分布及拉剪破坏区域图

拉应力破坏区主要分布在坡顶第四系内，最大深度约4.5m；坡体中部绿泥石英片岩向坡体内延伸最大深度约18m，在岩层交界处也存在部分拉应力破坏区。

剪切破坏区在坡顶、坡体中部和坡脚均有出现。坡顶向坡体内4.5m 的位置开始延伸最大深度为15m；坡体中部向坡体内延伸深度约为80m；坡脚最大深度约为22m。

（4）安全系数分析

强度折减法计算的安全系数为F=1.21，表明边坡处于极限平衡状态，在不受外界因素影响下是稳定的，符合一般规律，结果可靠。

（5）滑动机理分析

图13～14 为M2 模型强度折减法计算安全系数的过程，从强度折减系数F 取值为1.18、1.21、1.22 和1.25 计算出的边坡最大剪应变和剪切破坏分布情况，可以看出，边坡坡顶坡体中部及坡脚均存在剪切破坏区，随着折减系数增大，坡顶剪切破坏区范围向岩体内扩展，坡脚剪切破坏区逐步向上延伸，坡体中部的剪切破坏区同时向坡顶和坡脚发展，当折减系数增大到1.21 时，坡体中部与坡脚的剪切破坏区贯通，边坡中下部的绿泥石英片岩出边坡产生滑动，滑面形状为近似圆弧形，滑动模式为圆弧滑动。当折减系数增大到1.22 时，边坡发生整体蠕变滑动，并进一步向坡体内发展。

图13 M2 模型F=1.21 时最大剪应变分布图

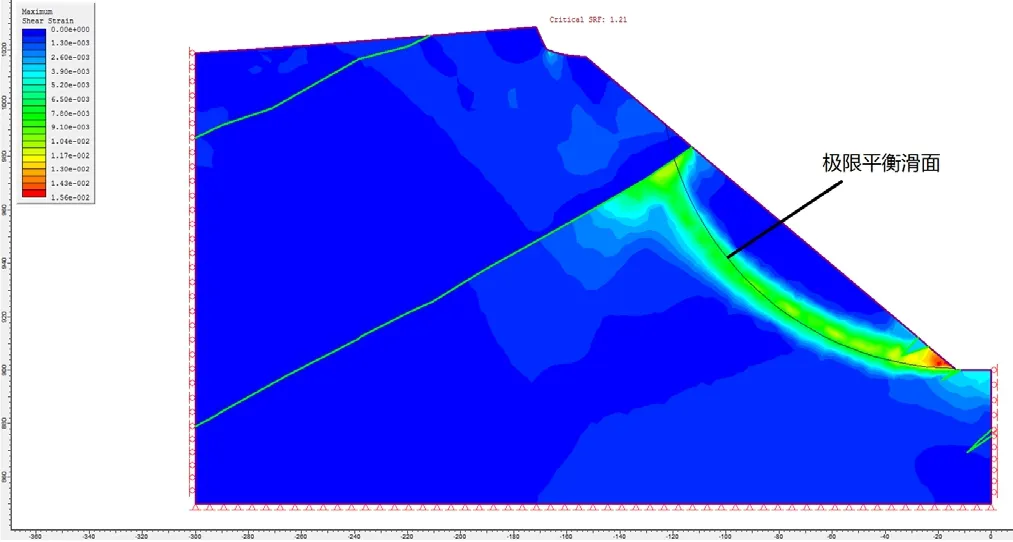
图14 M2 模型F=1.22 时最大剪应变分布图

3 总结

本文以巴彦哈尔金矿北露天边坡为研究对象，采用强度折减法计算了63 线、71 线剖面边坡安全系数，通过研究边坡破坏模式，进而推测边坡变形破坏规律，为边坡治理提供依据。

选取具有典型意义的能反映巴彦哈尔金矿北露天边坡稳定性的63 线（矿体下盘）和71 线（矿体上盘）工程地质剖面作为分析剖面。采用二维弹塑性有限元方法对这两个剖面进行有限元计算分析，计算得出的安全系数为1.21，因此，建议整体边坡角为当坑底标高为900 时，上盘40°，下盘42°。